Pure Mathematics
Vol.
09
No.
06
(
2019
), Article ID:
31608
,
8
pages
10.12677/PM.2019.96091
The Normal Families of Meromorphic Functions Which Share Set
Jinhua Cai, Guoqiang Dang
School of Mathematics and Information Science, Guangzhou University, Guangzhou Guangdong

Received: Jul. 11th, 2019; accepted: Jul. 21st, 2019; published: Aug. 7th, 2019

ABSTRACT
In this paper, it investigates the normality of a family of meromorphic functions sharing a set with their derivatives by using the Nevanlinna's value distribution theory and the method of Zalcman-Pang, and obtains the following main result: Let be a family of meromorphic functions in a domain D, , , where and are made up of finite complex numbers, and q be two positive integers. Suppose that for each , 1) every zero of is of multiplicities at least k, where ; 2) , then is normal in D.
Keywords:Meromorphic Functions, Normality, Shared Set

涉及分担集合的正规族
蔡金华,党国强
广州大学数学与信息科学学院,广东 广州

收稿日期:2019年7月11日;录用日期:2019年7月21日;发布日期:2019年8月7日

摘 要
使用Nevanlinna值分布理论和Zalcman-Pang方法讨论了涉及分担集合的亚纯函数的正规性,主要结果为:设
是区域D内的一族亚纯函数,
,
,
和
都是由有限复数组成的集合,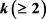 和q都是正整数。若对任意的
,满足:1)
的零点重级
,
;2)
,则
和q都是正整数。若对任意的
,满足:1)
的零点重级
,
;2)
,则 在D内正规。
在D内正规。
关键词 :亚纯函数,正规族,分担集合

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
定义D为一个区域,假设 为D内的一族亚纯函数,若对于 的任一函数序列 均可选出子序列 在D内按球面距离内闭一致收敛于一个亚纯函数,或者 ,则称 在D内正规(详见 [1] - [7] )。
a是复平面 上的一个复数,f和g是区域D内的两个亚纯函数,如果 和 在D内有相同的零点,则称f和g在D内IM分担a;若 和 在D有相同的零点,且所有的零点重级也相等,则称f和g在D内CM分担a。
1996年,方明亮 [8] 提出了分担集合的概念。
f和g是区域D内的两个亚纯函数, ,S是一个由三个有限复数组成的集合。定义
,其中 。如果 ,则称f和g分担集合S。
为区域D内的一族亚纯函数,我们称 在D内一点 正规,如果存在 的一个领域 ,使 在 内正规。
1992年,Schwick [9] 最早研究与分担值相关的亚纯函数族的正规性,证明了
定理A 设 为D上的一族亚纯函数, 是三个不同的有限复数。若对任意的 , ,其中 中, 在D内正规。
2000年,庞学诚和Zalcman [10] 改进了Schwick [9] 的结果,证明了
定理B 设 为D上的一族亚纯函数,a,b,c和d是有穷复数,且 和 。若对任意的 ,1) ;2) ,则 在D内正规。
如果 (定理A)替换成 ,是否能得到相同的结论。在这个方面,在2007年,刘晓俊与庞学诚 [11] 证明了以下的结果。
定理C 设 为D上的一族亚纯函数, 是三个不同的有限复数。若对任意的 , ,其中 ,则 在D内正规。
2002年,方明亮和Zalcman [12] 考虑了f和 分担一个值的情形,证明了
定理D 设 为D上的一族亚纯函数,a和b是两个非零有限复数,k是一个正整数。若对任意的 ,1) ;2) f的零点重级均 ,则 在D内正规。
如果我们把 (定理C)改为 ,自然地,我们会问是否存在相关的正规定则。在这个方面,在2011年,张汉等人 [13] 证明了以下的结果。
定理E 设 为D上的一族亚纯函数, , 是三个不同的有限复数, 是一个正整数,a为任意一个有限复数。若对任意的 ,1) ;2) 的零点与极点重级均 。
2016年,徐焱与仇惠玲 [14] 考虑f与 分担两个集合的亚纯函数的正规性,证明了
定理F 设 为单位圆盘 上的一族亚纯函数, , ,其中 都是有限复数且 。若对任意的 ,1) ;2) 存在一个正整数M,若 ,则 ,则 在 内正规。
2014年,李效敏 [15] 等人考虑f和 分担集合的情形,证明了
定理G 设 为D上的一族亚纯函数, 是一个正整数, 和 都是由有限复数组成的集合。若对任意的 ,1) ;2) 的零点重级均 ,则 在D内正规。
本文推广了李效敏 [15] 等人的结果,证明了
定理1 设 为D上的一族亚纯函数, 和q是一个正整数, 和 都是由
有限复数组成的集合。若对任意的 ,1) ;2) 的零点重级
均 ,则 在D内正规。
以下的例子(张汉等人 [13] )说明定理1中关于零点重级的限制是必要的。
例 设 为定义在单位圆盘 上的亚纯函数族,其中 , , ,
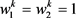 ,
和q是正整数。显然,对于
,有
,而
,
,
和q是正整数。显然,对于
,有
,而
,
根据Marty正规定则,可知 在 上不正规。
2. 引言
为了证明定理1,需要下列引理。
引理1 (Zalcman-Pang引理) [16] 设 为单位圆 内的一族亚纯函数,k和p均为正整数,如果对于 , 的零点重级 ,极点重级 ,且存在一个正数 ,若 ,必有 。那么,若 在单位圆内不正规,则对于每个 , ,存在
1) 函数列 ;
2) 点列 ;
3) 正数列 ;
4) 实数r, ,
使得函数 在复平面 上按球面距离内闭一致收敛于一个非常数亚纯函数
,并且 的零点重级 ,极点重级 ,它的级至多为2, 。
引理2 [1] [17] [18] 设f为有穷级的超越亚纯函数,b是一个非零复数,k为正整数,则f或者 有无穷多个零点。
引理3 [19] 设f为有理函数,则f能取任意复数,至多有一个Picard例外值,并且f有且仅有一个亏值。
引理4 [20] 设 是一个正整数,f是复平面上的一个有穷级的亚纯函数,且 的零点个数是有限的,则f的极点个数是有限个。
3. 定理1的证明
证明:假设 在D内不正规,则存在一点 ,使 在 处不正规则。由引理1,可知存在函数列 ,点列 ,正数列 ,使得函数
(1)
(2)
在复平面 上按球面距离内闭一致收敛,其中 是一个非常数亚纯函数, 和 的级至多为2,且它们的零点重级均 。
下面我们分两种情形进行讨论。
情形1。存在 ,使 , 或 , ,不失一般性,我们假设 。
令 。根据已知条件,可知 的零点重级至少为k。取 ,使 在邻域 内是全纯的,否则, 在 上内闭一致收敛于全纯函数 。接下来我们证明 在 处不正规。因为 是一个非常数亚纯函数,所以 ,则存在一点 ,使 。根据Hurwitz定理,可知存在一个点列 且 ,使 。当 时, 。故对任一 ,存在一个正数 ,使 。从而
矛盾。
如果 ,也就是说 。根据条件,可得 ,
则存在 ,使得 ,由此可知,若 ,则 。假设 。
根据引理1,则存在正数列 ;复数列 ;子序列 ;使 在 上按球面距离内闭一致收敛到非常数亚纯函数 ,其中 的零点重级均 ,级至多为2,且
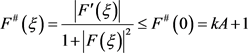 。
。
我们断言:
1) 在复平面 , 的零点个数是有限的;
2) 。
令 是 的l重零点。若 零点个数是无穷多个,可取 的 个互不相同的零点 。由于 ,根据Hurwitz定理,可得存在 ,使得 ,也就是说,当 时, 。根据Hurwitz定理, 是 的至少 重零点,矛盾。故断言1)成立。
若 ,由Hurwitz定理,可知存在一点列 ,使得 。由条件可得
则 。因此证明了 。
如果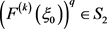 ,也就是说,存在某个
,使
。可证
,否则,
,也就是说,存在某个
,使
。可证
,否则,
,则 是一个次数至多为k的多项式。因为 的零点重级 ,可得 是一个
次数为k的多项式,令 。
当 时,
这说明 。如果 ,可得 ,上面不等式也成立。与 矛
盾。因为 ,根据Hurwitz定理,可知存在一点列 , ,使得
。根据条件可得,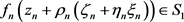 。可证,当
。可证,当
时, 。否则, 。于是,
这与 矛盾,这暗示了,若 ,则 。
根据断言1)和引理2,可知 不是超越亚纯函数。
情形1.1 是一个非常数的多项式。
根据Nevanlinna第二基本定理和断言2),可知
(3)
显然,
(4)
因为F的零点重级至少为k,可知
(5)
由F的零点重级至少为 ,(3),(4)和(5),可得
 (6)
(6)
(7)
由于 的零点重级均 ,可知 仅有一个零点或者仅有两个不同的零点。
情形1.1.1 仅有一个零点。
令 ,其中 为非零常数,对任意的 , 至少有一个零点。根据断言2),可知 至少有两个不同的零点。
情形 1.1.2 仅有两个不同的零点。
根据
的零点重级均 和(6),可知
,从而
。因此
和
,由此可知
是一个次数为4~的多项式,且
的两个不同零点的重级都为2。可证
,
。由断言2),如果
,
,这说明
不是
的重级为2的零点,矛盾。根据
和
仅有两个不同的零点,可知
的每个零点重级为2。
和(6),可知
,从而
。因此
和
,由此可知
是一个次数为4~的多项式,且
的两个不同零点的重级都为2。可证
,
。由断言2),如果
,
,这说明
不是
的重级为2的零点,矛盾。根据
和
仅有两个不同的零点,可知
的每个零点重级为2。
显然, ,令
(8)
显然, 是有理函数,它的极点来自于 零点, 。如果 是 的二~重零点,则 是 的一重零点,也是 的二重零点,这意味着 零点也是P的零点,所以P没有极点,且P是多项式。由(8),可知 ,经过简单的计算,可得 ,所以P仅有一个零点。对于任一 ,若 ,则 ,这说明P至少有两个不同的零点,矛盾。
情形1.2 不是多项式的非常数有理函数。
令
(9)
其中 是复数,m是一个正整数, 和 是互素的两个多项式,且 。
假设
(10)
其中 是一个常数,t是一个正整数, 是t个正整数, 是t个不同的有限复数, 。由(9)和(10),可得到
(11)
(12)
情形1.2.1 假设 。
由Nevanlinna第二基本定理,断言1)和断言2),可知
(13)
由(9),(10)和 的零点重级均 ,可得
(14)
和
(15)
结合(12)~(15),可得 。经过简单的计算,获知
. (16)
由于m,w和t都是正整数,根据(16),可知 ,与 矛盾。
情形1.2.2 假设 。
从(9)~(14)可知
且 ,因此 矛盾。
情形2 且 。
根据引理3,可断言g是超越亚纯函数。从(1)和(2),获知
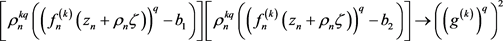 (17)
(17)
在复平面 上内闭一致收敛。可证 。如果 ,可知 是一个次数至多为 ,
这与 是超越亚纯函数矛盾。结合 ,(1),(2),(17), 和
,可得 ,即 。
根据g的级至多为2和引理4,可知,在复平面 上,g极点个数是有限的。由Nevanlinna第二基本定理,获知
(18)
从(18)可知,g是一个有理函数。矛盾。
综上所述, 在D内正规,定理1证毕。
基金项目
国家自然科学基金(编号:11271090),广东省自然科学基金(编号:2016A030310257、2015A030313346),广州大学研究生创新能力培养资助计划(2018GDJC-D28)资助。
文章引用
蔡金华,党国强. 涉及分担集合的正规族
The Normal Families of Meromorphic Functions Which Share Set[J]. 理论数学, 2019, 09(06): 686-693. https://doi.org/10.12677/PM.2019.96091
参考文献
- 1. Gu, Y.X., Fang, M.L. and Pang, X.C. (2007) The Theory of Normal Families and It’s Applications. Science Press, Beijing.
- 2. Ahlfors, L.V. (1979) Complex Analysis. 3rd Edition, McGraw-Hill, Hoboken.
- 3. Schiff, J. (1993) Normal Families. Springer-Verlag, Berlin.
https://doi.org/10.1007/978-1-4612-0907-2 - 4. Xu, J.F. and Cao, W.S. (2010) Some Normality Criteria of Meromorphic Functions. Journal of Inequalities and Applications, 2010, Article ID: 926302.
https://doi.org/10.1155/2010/926302 - 5. Chen, H.H., Cai, J.H. and Yuan, W.J. (2018) Normality Criteria of a Family of Meromorphic Functions Concerning Shared Set. Journal of Jiaying University, 36, 5-8.
- 6. Jiang, Y.B. and Gao, Z.S. (2011) Normal Families of Meromorphic Functions Sharing Values or Functions. Journal of Inequalities and Applications, 2011, Article No. 72.
https://doi.org/10.1186/1029-242X-2011-72 - 7. Qiu, L. and Hu, F.F. (2013) Normal Families of Meromorphic Functions Sharing One Function. Journal of Inequalities and Applications, 2013, 288.
https://doi.org/10.1186/1029-242X-2013-288 - 8. Fang, M.L. (1996) A Note on Sharing Values and Normality. Journal of Mathematical Study, 29, 29-32.
- 9. Schwick, W. (1992) Sharing Values and Normality. Archiv der Mathematik, 59, 50-54.
https://doi.org/10.1007/BF01199014 - 10. Pang, X.C. and Zalcman, L. (2000) Normality and Shared Values. Arkiv för Matematik, 38, 171-182.
https://doi.org/10.1007/BF02384496 - 11. Liu, X.J. and Pang, X.C. (2007) Shared Values and Normality. Acta Mathematica Sinica, 52, 409-412.
- 12. Fang, M.L. and Zalcman, L. (2002) Normal Families and Shared Values of Meromorphic Functions. Computational Methods and Function Theory, 2, 385-395.
https://doi.org/10.1007/BF03321856 - 13. Zhang, H., Xie, D. and Zhang, Q.D. (2011) Normal Criteria Concerning Shared Values of Meromorphic Function. Acta Mathematica Scientia A, 31, 1290-1294.
- 14. Xu, Y. and Qiu, H.L. (2016) Normal Functions and Shared Sets. Filomat, 30, 287-292.
https://doi.org/10.2298/FIL1602287X - 15. Li, X.M., Yi, H.X. and Wang, K.M. (2014) Notes on Normal Families of Meromorphic Functions Sharing a Set with Their Derivatives. Bulletin of the Korean Mathematical Society, 51, 1773-1789.
https://doi.org/10.4134/BKMS.2014.51.6.1773 - 16. Pang, X.C. and Zalcman, L. (2000) Normal Families and Shared Values. Bulletin of the London Mathematical Society, 32, 325-331.
https://doi.org/10.1112/S002460939900644X - 17. Bergweiler, W. and Eremenko, A. (1995) On the Singularities of the Inverse to a Meromorphic Functions of Finite Order. Revista Matemática Iberoamericana, 11, 355-372.
https://doi.org/10.4171/RMI/176 - 18. Zalcman, L. (1998) Normal Families: New Perspective. Bulletin of the American Mathematical Society, 35, 215-230.
https://doi.org/10.1090/S0273-0979-98-00755-1 - 19. Yang, L. (1982) Value Distribution Theory and It’s New Research. Science Press, Beijing.
- 20. Langley, J.K. (2003) The Second Derivative of a Meromorphic Function of Finite Order. Bulletin of the London Mathematical Society, 35, 97-108.
https://doi.org/10.1112/S0024609302001558