Pure Mathematics
Vol.
09
No.
07
(
2019
), Article ID:
31982
,
8
pages
10.12677/PM.2019.97102
Lie Super-Bialgebra Structures on a Super Heisenberg-Virasoro Algebra
Meijun Li
School of Mathematics and Statistics, Qingdao University, Qingdao Shandong

Received: Aug. 6th, 2019; accepted: Aug. 26th, 2019; published: Sep. 2nd, 2019

ABSTRACT
In this paper we investigate Lie super-bialgebra structures on a super Heisenberg-Virasoro algebra. We obtain sufficient and necessary conditions for this type Lie super-bialgebra structures to be triangular coboundary.
Keywords:Lie Super-Bialgebras, Yang-Baxter Equations, A Super Heisenberg-Virasoro Algebra
一类超Heisenberg-Virasoro代数的超双代数 结构
李美君
青岛大学数学与统计学院,山东 青岛

收稿日期:2019年8月6日;录用日期:2019年8月26日;发布日期:2019年9月2日

摘 要
本文主要研究了一类超Heisenberg-Virasoro代数上的超双代数结构,得到了该类超李双代数为三角余边缘的充分必要条件。
关键词 :超李双代数,Yang-Baxter方程,超Heisenberg-Virasoro代数

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
为了研究量子群,Drinfeld于1983年在文献 [1] [2] 中引入了李双代数。无限维李代数的双代数结构无法统一分类,文献 [3] 引入了构造三角余边缘李双代数的方法,文献 [4] 构造了Witt型和Virasoro型李双代数,文献 [5] 给出了相应分类。文献 [6] [7] [8] 研究了Schrödinger-Virasoro李代数、广义Witt型李代数和Virasoro李代数等无限维李代数的双代数结构。本文将研究超Heisenberg-Virasoro代数
上的超双代数
结构,它是复数域
上的无限维李超代数,以
为一组基,且满足以下运算
(1.1)
2. 预备知识
给定超向量空间
,假设以下元素都是
-分次的,用
表示x的次,即
。引入
,,。
定义2.1:李超代数
由超向量空间L和双线性映射
构成,且满足
,,。
定义2.2:李超余代数
由超向量空间L和线性映射
构成,且满足
,,。
定义2.3:李超双代数
满足:
是李超代数,
是超余代数,且有
,
,其中“
”表示对角伴随作用
(2.1)
用
表示L的泛包络代数,记
,引入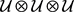 的元素
的元素
,
, . (2.2)
其中
是泛包络代数
的单位元,则定义
如下
, .
定义2.4:1) 余边缘李超双代数
是一个四元组,其中
是李超双代数,并且有
,使得
(称为r的余边缘),即对任意
,有
。
2) 我们称
为三角的,若满足经典的Yang-Baxter方程 (CYBE)
(2.3)
3) 元素
称为满足修正的Yang-Baxter方程,如果
, (2.4)
文献 [1] 给出了以下两个结果,元素r满足(2.3)当且仅当满足(2.4)。设L是李超代数,且
,则有
,三元组
是李双代数当且仅当r满足(2.3)。
我们可把
看作对角伴随作用下的
-模。用
表示导子
的集合,且D满足
, (2.5)
导子是偶(奇)的,若
。用
表示内导子
的集合,其中
。用
表示李代数
系数在
-模
上的一阶上同调群,则
。
表示非零整数且
。对任意
,我们可引入以下导子
,,, ,
,
. (2.6)
表示
,即
。
3. 主要结果及证明过程
本文的主要结果可表述为以下两个定理。
定理3.1:
。
定理3.2:李双代数
是三角余边缘的当且仅当
。
引理3.1:把
的n次张量积
看作
对角伴随作用下的
-模。如果对某个
和任意
,使得
,则
。
证明:可运用文献 [1] [5] 相应结论的证明得到。
引理3.2:对所有
,假设
,使得
,则对某个
,有
。
证明:可运用文献 [6] 中引理3.2的技巧得证。
定理3.1:由断言1~4得到。
断言1:如果
,则
。
证明:首先记
,。把
作用在
上,再利用
,有
,,从而
为内导子。
断言2:
。
证明:把
作用在
上,
,,有
。则由引理3.1可推出
。
类似地,通过将
作用于
上,有
。
断言3:当
时,用
(
)代替
,我们可假设 。
。
证明:对
,, 和
如下所示
,
,
,
其中,所有张量积的系数都在复数域
中,且它们的和是有限的。对于
,下列恒等式成立,
,
,,
,,
用
代替
,其中u是
,,, 和
(
)的适当的线性组合,假设对任意
,, 和
,有
。则
化简为
.
将
作用在
上,有
,,,, (3.1)
,,,,
,, .
从而,进一步得到
的简化式如下
,
.
将
作用在
上,结合(3.1)得
,,, (3.2)
,, . (3.3)
将
作用在
上,有
,
,,,,
此时,由(3.2)和(3.3)得
, (3.4)
. (3.5)
将
作用在
上,结合(3.4)和(3.5)得,则有
,
,,,,
,,, .
记
,,,用
代替D,有
。则有
,
.
且系数满足以下关系式
,
.
将
作用在
上,有
,
,,,,
,, .
将
作用在
上,同理有
.
将
作用在
上,有
, .
此时,
。
将
作用在
和
上,可得
,
.
将
作用在
和
上,分别有以下系数关系式
,,,,
,,, .
将
作用在
和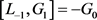 上,我们可以推导出
上,我们可以推导出
,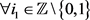 ,
,
, .
且有
。
将
作用在
和
上,可得
,
从而有
。
将
作用在
上,有
,
。
且满足
,。
根据以下记法:
,,,,,,利用数学归纳法,并考虑(1.1)中所有的李括号可得
,,
,
,, .
断言4:当
时,用
(
)代替
,我们可假设
。
证明:对
,, 和
如下所示
,
,
,
其中,所有张量积的系数都在复数域
中,且它们的和是有限的。对于
,下列恒等式成立,
,,
, .
用
代替
,其中u是
,, 和
的适当的线性组合,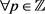 ,假设对于任意
, 和
,有
。则
可写成
,假设对于任意
, 和
,有
。则
可写成
.
将
作用在
上,记
,,用
代替D,可得
.
将
依次作用在
, 和
上,
我们可以推导出
如下
.
且系数满足以下关系
, (3.6)
(3.7)
.(3.8)
将
依次作用在
, 和
上,我们可将
化简为
.
将
作用在
和
上,可得
.
将
作用在
和
上,再结合(3.6)~(3.8),可以推导出
,
.
将
作用在
上,有
。
将
作用在
上,有
。
根据以下记法:
,利用数学归纳法,并考虑(1.1)所有李括号可推导出
,,, .
则定理3.1最终由归纳法
可证得。
设
是
上的超李双代数结构。由定理3.1得,在(2.6)中提到对某个
,有
当且仅当
。结合
和引理3.2,可以推导出对某个
,有
,则引理3.1得出
。因此,
是一个三角余边缘的超李双代数当且仅当
。故定理3.2得证。
文章引用
李美君. 一类超Heisenberg-Virasoro代数的超双代数结构
Lie Super-Bialgebra Structures on a Super Heisenberg-Virasoro Algebra[J]. 理论数学, 2019, 09(07): 783-790. https://doi.org/10.12677/PM.2019.97102
参考文献
- 1. Drinfeld, V.G. (1983) Constant Quasiclassical Solutions of the Yang-Baxter Quantum Equation. Soviet Mathematics Doklady, 28, 667-671.
- 2. Belavin, A.A. and Drinfeld, V.G. (1982) Solutions of the Classical Yang-Baxter Equation for Simple Lie Algebras. Functional Analysis and Its Applications, 16, 159-180.
https://doi.org/10.1007/BF01081585
- 3. Michaelis, W. (1994) A Class of Infinite-Dimensional Lie Bialgebras Containing the Virasoro Algebras. Advances in Mathematics, 107, 365-392.
https://doi.org/10.1006/aima.1994.1062
- 4. Taft, E.J. (1993) Witt and Virasoro Algebras as Lie Bialgebras. Journal of Pure and Applied Algebra, 87, 301-312.
https://doi.org/10.1016/0022-4049(93)90116-B
- 5. Ng, S.H. and Taft, E.J. (2000) Classification of the Lie Bialgebra Structures on the Witt and Virasoro Algebras. Journal of Pure and Applied Algebra, 151, 67-88.
https://doi.org/10.1016/S0022-4049(99)00045-6
- 6. Han, J.Z., Li, J.B. and Su, Y.C. (2009) Lie Bialgebra Structures on the Schrödinger-Virasoro Lie Algebra. Journal of Mathematical Physics, 50, Article ID: 083504.
https://doi.org/10.1063/1.3187784
- 7. Song, G.A. and Su, Y.C. (2006) Lie Bialgebras of Generalized Witt Type. Science in China: Series A, 49, 533-544.
https://doi.org/10.1007/s11425-006-0533-7
- 8. Wu, Y.Z., Song, G.A. and Su, Y.C. (2006) Lie Bialgebras of Generalized Virasoro-Like Type. Acta Mathematica Sinica, English Series, 22, 1915-1922.
https://doi.org/10.1007/s10114-005-0742-y







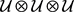 的元素
的元素 。
。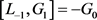 上,我们可以推导出
上,我们可以推导出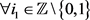 ,
,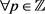 ,假设对于任意
, 和
,有
。则
可写成
,假设对于任意
, 和
,有
。则
可写成