Frobenius扩张下的(F,A)-Gorenstein平坦模 (F,A)-Gorenstein Flat Modules under Frobenius Extension

doi:10.12677/PM.2023.136159

Pure Mathematics
Vol. 13 No. 06 ( 2023 ), Article ID: 67152 , 7 pages
10.12677/PM.2023.136159

Frobenius扩张下的 $(F, A)$ -Gorenstein平坦模

魏玉娟^*，周彩霞

●How to Cite this Article

西北师范大学数学与统计学院，甘肃兰州

收稿日期：2023年5月5日；录用日期：2023年6月5日；发布日期：2023年6月13日

摘要

设 $R \subseteq S$ 是环的Frobenius扩张，M是任意左S-模，假设 $A$ 是右R-模的类， $B$ 是右S-模的类，且 $G F_{(F, B)}$ 关于扩张封闭， $I (S^{O P}) \subseteq B$ , 在一些条件下证明了M是 $(F, B)$ -Gorenstein平坦左S-模当且仅当M是 $(F, A)$ -Gorenstein平坦左R-模当且仅当 $S \otimes_{R} M$ 是 $(F, B)$ -Gorenstein平坦左S-模。

关键词

Frobenius扩张， $(F, A)$ -Gorenstein平坦模， $(F, A)$ -Gorenstein平坦维数

$(F, A)$ -Gorenstein Flat Modules under Frobenius Extension

Yujuan Wei^*, Caixia Zhou

College of Mathematics and Statistics, Northwest Normal University, Lanzhou Gansu

Received: May 5^th, 2023; accepted: Jun. 5^th, 2023; published: Jun. 13^th, 2023

ABSTRACT

Let $R \subseteq S$ be a Frobenius extensin of rings, M be any left S-modules. Let $A$ be class of right R-modules and $B$ be class of right S-modules. $G F_{(F, B)}$ be closed by extension, $I (S^{O P}) \subseteq B$ , under some conditions proved that M be $(F, B)$ -Gorenstein flat left S-modules if and only if M be $(F, A)$ -Gorenstein flat left S-modules if and only if $S \otimes_{R} M$ be $(F, B)$ -Gorenstein flat left S-modules.

Keywords:Frobenius Extensin, $(F, A)$ -Gorenstein Flat Module, $(F, A)$ -Gorenstein Flat Dimension

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

作为平坦模的推广，1993年，Overtoun等 [1] 引入了Gorenstein平坦模的概念，研究了其性质。2009年，Holm和Jorgensen [2] 引入了对偶对的概念。2019年，Gillespie [3] 引入了相对于对偶对 $(L, A)$ 的Gorenstein投射、内射和平坦模的概念。2022年，Becerril [4] 进一步研究了 $(F, A)$ -Gorenstein平坦模的同调性质及其维数。

1954年，Kasch [5] 引入了Frobenius扩张的概念。1960年，Nakayam，Tsuzuku [6] 和Morita [7] 对Frobenius扩张做了更深入的研究。近年来，Ren [8] 引入了可分Frobenius扩张的概念，研究了在环的Frobenius扩张下Gorenstein投射模与Gorenstein投射维数，证明了左S-模M是Gorenstein投射模当且仅当M作为左R-模也是Gorenstein投射模。2019年，Ren [9] 研究了在环的Frobenius扩张 $R \subseteq S$ 下，其中S-是右凝聚环，Gorenstein平坦模与Gorenstein平坦维数的同调不变性。

受以上结论的启发，本文研究了在环的Frobenius扩张下 $(F, A)$ -Gorenstein平坦模与 $(F, A)$ -Gorenstein平坦维数的同调不变性。

文中环R和S-均指有单位元的结合环，模均指酉模。R-模(或者S-模)表示所有的左R-模(或者左S-模)。R^op-模(或者S^op-模)表示所有的右R-模(或者右S-模)。对任意的环R， $M o d (R)$ 表示所有左R-模的范畴， $M o d (R^{o p})$ 表示所有右R-模的范畴。 $I (R)$ 表示所有内射左R-模构成的类。 $F (R)$ 表示所有平坦左R-模构成的类。

在本文中， $A$ 表示所有右R-模构成的类， $B$ 表示所有右S-模构成的类，且 $I (S^{o p}) \subseteq B$ 。

2. $(F, A)$ -Gorenstein平坦模

定义2.1 ( [9] 定义2.1)称 $R \subseteq S$ 是环的Frobenius扩张，如果满足下面五条等价条件中的一条

1) 函子 $S \otimes_{R} -$ 和 $H o m_{R} (S, -)$ 是自然等价的；

2) 函子 $- \otimes_{R} S$ 和 $H o m_{R^{o p}} (S, -)$ 是自然等价的；

3) ${}_{R}S$ 是有限生成投射模，且 ${}_{S}S_{R} ≅ H o m_{R} ({}_{R}S_{S}, R)$ ；

4) $S_{R}$ 是有限生成投射模，且 ${}_{R}S_{S} ≅ H o m_{R} ({}_{S}S_{R}, R)$ ；

5) 存在R-同态 $ξ : S \to R$ 和 $X_{i}, Y_{i} \in S$ ，使得对任意 $s \in S$ ， $\sum_{i} X_{i} ξ (Y_{i} s) = s$ 和 $\sum_{i} ξ (s X_{i}) Y_{i} = s$ 。

定义2.2 设M是左R-模，称M是 $(F, A)$ -Gorenstein平坦模，如果存在平坦左R-模的正合列

$F : \dots \to F_{1} \to F_{0} \to F^{0} \to F^{1} \to \dots$ ，

使得 $M ≅ K e r (F^{0} \to F^{1})$ ，且对任意 $A \in A$ ， $A \otimes_{R} F$ 正合。

通常，我们将 $(F, A)$ -Gorenstein平坦模类记为 $G F_{(F, A)} (R)$ 。

引理2.3 设 $R \subseteq S$ 是环的Frobenius扩张，M是任意左S-模，假设以下成立

1) 任意 $A \in A$ ， $A \otimes_{R} S \in B$ ；

2) 任意 $B \in B$ ， $B \in A$ ；

3) 任意 $B \in B$ ，B是右S-模 $H o m_{R^{o p}} (S, B)$ 的直和项。

若M是 $(F, B)$ -Gorenstein平坦左S-模，则M也是 $(F, A)$ -Gorenstein平坦左R-模。

证明设M是 $(F, B)$ -Gorenstein平坦左S-模，则存在平坦左S-模的正合复形

$F = \dots \to F_{1} \to F_{0} \to F^{0} \to F^{1} \to \dots$ ，

使得 $M ≅ K e r (F^{0} \to F^{1})$ ，且对任意 $B \in B$ ， $B \otimes_{S} F$ 是正合的。因为任意平坦左S-模都是平坦左R-模，所以F是平坦左R-模的正合复形。

令 $A \in A \subseteq M o d (R^{o p})$ ，因为 $A \otimes_{R} S ≅ H o m_{R^{O P}} (S, A)$ ，且 $H o m_{R^{O P}} (S, A)$ 是右S-模，所以 $H o m_{R^{O P}} (S, A) \otimes_{S} F$ 正合，又由同构 $A \otimes_{R} F ≅ A \otimes_{R} S \otimes_{S} F ≅ H o m_{R^{O P}} (S, A) \otimes_{S} F$ 知， $A \otimes_{R} F$ 是正合的，所以M是 $(F, A)$ -Gorenstein平坦左R-模。

引理2.4 设 $R \subseteq S$ 是环的Frobenius扩张，M是任意左S-模，假设以下成立：

1) 任意 $A \in A$ ， $A \otimes_{R} S \in B$ ；

2) 任意 $B \in B$ ， $B \in A$ ；

3) 任意 $B \in B$ ，B是右S-模 $H o m_{R^{o p}} (S, B)$ 的直和项。

若M是 $(F, A)$ -Gorenstein平坦左R-模，则 $S \otimes_{R} M$ 是 $(F, B)$ -Gorenstein平坦左S-模。

证明设M是 $(F, A)$ -Gorenstein平坦左R-模，则存在平坦左R-模的正合复形

$F : \dots \to F_{1} \to F_{0} \to F^{0} \to F^{1} \to \dots$

使得 $M ≅ K e r (F^{0} \to F^{1})$ ，且对任意 $A \in A$ ， $A \otimes_{R} F$ 正合。由( [10] 定理2.1.13)，知 $S \otimes_{R} F$ 是平坦左S-模的正合复形，且 $S \otimes_{R} M ≅ K e r (S \otimes_{R} F^{0} \to S \otimes_{R} F^{1})$ 。对任意 $B \in B$ ，由同构 $B \otimes_{R} F ≅ B \otimes_{S} S \otimes_{R} F$ 知， $B \otimes_{S} S \otimes_{R} F$ 正合，因此 $S \otimes_{R} M$ 是 $(F, B)$ -Gorenstein平坦左S-模。

引理2.5 ( [4] Lemma 3.11)设 $A \subseteq M o d (R^{o p})$ ， $I (R^{O P}) \subseteq A$ ，以下等价

1) $G F_{(F, A)}$ 关于扩张封闭；

2) $G F_{(F, A)}$ 是预可解的；

3) $0 \to G_{1} \to G_{0} \to M \to 0$ 是左R-模的正合序列，其中 $G_{0}, G_{1} \in G F_{(F, A)}$ ，如果对任意 $A \in A$ ， $T o r_{1}^{R} (A, M) = 0$ ，则 $M \in G F_{(F, A)}$ 。

命题2.6 若 $G F_{(F, A)}$ 关于扩张封闭，且 $I (R^{O P}) \subseteq A$ ，则 $G F_{(F, A)}$ 关于直和和直和项封闭。

命题2.7 设 $R \subseteq S$ 是环的Frobenius扩张，L是任意左S-模， $G F_{(F, B)}$ 关于扩张封闭， $I (R^{O P}) \subseteq B$ ，假设以下成立

1) 对任意 $A \in A$ ， $A \otimes_{R} S \in B$ ；

2) 对任意 $B \in B$ ， $B \in A$ ；

3) 对任意 $B \in B$ ，B是右S-模 $H o m_{R^{o p}} (S, B)$ 的直和项。

则L是 $(F, A)$ -Gorenstein平坦左R-模，当且仅当 $S \otimes_{R} L$ 是 $(F, B)$ -Gorenstein平坦左S-模。

证明 $\Rightarrow$ )由引理2.4易知。

$\Leftarrow$ )若 $S \otimes_{R} L$ 是 $(F, B)$ -Gorenstein平坦左S-模，由引理2.3知， $S \otimes_{R} L$ 也是 $(F, A)$ -Gorenstein平坦左R-模，设L是左S-模，则有自然满同态 $π : S \otimes_{R} L \to L$ ， $π (s \otimes l) = s l$ ，当看作R-同态时， $π$ 可裂，因此 ${}_{R}L$ 是 ${}_{R}{(S \otimes_{R} L)}$ 的直和项，又由命题2.6知 $(F, A)$ -Gorenstein平坦左R-模关于直和项封闭，所以L是 $(F, A)$ -Gorenstein平坦左R-模。

命题2.8 设M是左R-模，以下等价：

1) M是 $(F, A)$ -Gorenstein平坦模；

2) 对任意 $A \in A$ 及整数 $i \geq 1$ ， $T o r_{R}^{i} (A, M) = 0$ ，且M存在 $A \otimes_{R} -$ 正合的右平坦分解；

3) 存在短正合序列 $0 \to M \to F \to K \to 0$ ，其中 $F \in F (R)$ ，则 $K \in G F_{(F, A)}$ 。

证明 (1) $\Rightarrow$ (2)易得。

(3) $\Rightarrow$ (2)因为 $K \in G F_{(F, A)}$ ，所以对任意 $A \in A$ 及整数 $i \geq 1$ ， $T o r_{R}^{i} (A, K) = 0$ ，且K存在 $A \otimes_{R} -$ 正合的

右平坦分解，

$0 \to K \to F_{0} \to F_{1} \to \dots$ ， ①

将短正合序列 $0 \to M \to F \to K \to 0$ 与正合序列①连接起来，存在M的一个 $A \otimes_{R} -$ 正合的右平坦分

解，

$0 \to M \to F \to F_{0} \to F_{1} \to \dots$ ， ②

将 $A \otimes_{R} -$ 作用于短正合序列 $0 \to M \to F \to K \to 0$ ，可得长正合序列

$\dots \to T o r_{R}^{i + 1} (A, F) \to T o r_{R}^{i + 1} (A, K) \to T o r_{R}^{i} (A, M) \to T o r_{R}^{i} (A, F) \to T o r_{R}^{i} (A, K) \to \dots$ ，

从而 $T o r_{R}^{i + 1} (A, K) ≅ T o r_{R}^{i} (A, M) = 0$ 。

定理2.9 设 $R \subseteq S$ 是环的Frobenius扩张， $G F_{(F, B)}$ 关于扩张封闭， $I (R^{O P}) \subseteq B$ ，M是任意左S-模，假设以下成立

1) 任意 $A \in A$ ， $A \otimes_{R} S \in B$ ；

2) 任意 $B \in B$ ， $B \in A$ ；

3) 任意 $B \in B$ ，B是右S-模 $H o m_{R^{o p}} (S, B)$ 的直和项。

则M是 $(ℱ, ℬ) -$ Gorenstein平坦左S-模，当且仅当M是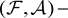Gorenstein平坦左R-模。

证明 $\Rightarrow$ )显然。

$\Leftarrow$ )设M是 $(F, A)$ -Gorenstein平坦左R-模，则对任意 $A \in A$ 及整数 $i > 0$ ， $T o r_{i}^{R} (A, M) = 0$ 。由于对任意 $B \in B$ ，B是右S-模 $H o m_{R^{o p}} (S, B)$ 的直和项，因此由同构

$T o r_{i}^{S} (H o m_{R^{o p}} (S, B), M) ≅ T o r_{i}^{S} (B \otimes_{R} S, M) ≅ T o r_{i}^{R} (B, M) = 0$

可知 $T o r_{i}^{S} (B, M) = 0$ 。

由命题2.8可知，我们只需要构造 ${}_{S}M$ 的向右的一个平坦分解，由引理2.4知， $S \otimes_{R} M$ 是 $(F, B)$ -Gorenstein平坦左S-模，又因 $S \otimes_{R} M ≅ H o m_{R} (S, M)$ ，所以存在左S-模的短正合序列

$0 \to H o m_{R} (S, M) \overset{f}{\to} F^{0} \to K \to 0$

其中 $F^{0}$ 是平坦模，K是 $(F, B)$ -Gorenstein平坦左S-模，另外，有S-模单同态 $φ : M \to H o m_{R} (S, M)$ ， $φ (m) (s) = s m$ ，将 $φ$ 限制在R-同态上， $φ$ 可裂，于是存在 $φ^{'} : H o m_{R} (S, M) \to M$ ，使得 $φ^{'} φ = 1_{M}$ ，考虑左S-模的短正合序列

$0 \to M \overset{f φ}{\to} F^{0} \to K^{0} \to 0$

其中 $K^{0} = C o k e r (f φ)$ 。由引理2.3知，K是 $(F, A)$ -Gorenstein平坦左R-模，则对任意 $A_{1} \in A$ 及整数 $i > 0$ ， $T o r_{i}^{R} (A_{1}, K) = 0$ 。从而 $A_{1} \otimes_{R} f : A_{1} \otimes_{R} H o m_{R} (S, M) \to A_{1} \otimes_{R} F^{0}$ 是单同态，同时， $A_{1} \otimes_{R} φ : A_{1} \otimes_{R} M \to A_{1} \otimes_{R} H o m_{R} (S, M)$ 也是单同态，因此序列

$0 \to A_{1} \otimes_{R} M \to A_{1} \otimes_{R} F^{0} \to A_{1} \otimes_{R} K^{0} \to 0$

是正合的，故 $T o r_{1}^{R} (A_{1}, K^{0}) = 0$ ，从而由引理2.5可得， $K^{0}$ 是 $(F, A)$ -Gorenstein平坦左R-模。用类似的方法，我们可以证得对任意 $B \in B$ ， $T o r_{1}^{S} (B, K^{0}) = 0$ ，从而序列

$0 \to B \otimes_{S} M \to B \otimes_{S} F^{0} \to B \otimes_{S} K^{0} \to 0$

是正合的。

对 $K^{0}$ 重复以上步骤，可以得到一个在函子 $B \otimes_{S} -$ 作用后依旧保持正合的短正合序列

$0 \to K^{0} \to F^{1} \to K^{1} \to 0$ ，

其中 $F^{1}$ 是平坦模， $K^{1}$ 作为R-模是 $(F, A)$ -Gorenstein平坦左R-模，通过归纳法，可以构造出 ${}_{S}M$ 的向右的一个平坦分解，

$0 \to M \to F^{0} \to F^{1} \to \dots$ ①

其中 $F^{i}$ 是平坦模，且对任意 $B \in B$ ，序列①在函子 $B \otimes_{S} -$ 的作用下保持正合。因此M是 $(F, B)$ -Gorenstein平坦左S-模。

3. $(F, A)$ -Gorenstein平坦维数

定义3.1 设M是任意左R-模，定义M的 $(F, A)$ -Gorenstein平坦维数为M的 $(F, A)$ -Gorenstein平坦维数的最短长度，即 $G f d_{(F, A)} (M) \leq n$ 当且仅当存在左R-模的正合序列

$0 \to L_{n} \to L_{n - 1} \to \dots \to L_{0} \to M \to 0$

其中n是非负整数， $L_{i} (i = 0, 1, \dots, n)$ 是 $(F, A)$ -Gorenstein平坦模。

如果这样的n不存在，则 $G f d_{(F, A)} (M) = \infty$ 。

引理3.2 由( [4] 定理3.12)可得 $(F, A)$ -Gorenstein平坦维数的另一种定义

$G f d_{(F, A)} (M) = \sup {i \in N | 存在 A \in A, 使得 T o r_{i}^{R} (A, M) = 0}$

定理3.3 设 $R \subseteq S$ 是环的Frobenius扩张， $G F_{(F, B)}$ 关于扩张封闭， $G f d_{(F, B)} (M) < \infty$ ， $I (R^{O P}) \subseteq B$ ，M是左S-模，假设以下成立

1) 任意 $A \in A$ ， $A \otimes_{R} S \in B$ ；

2) 任意 $B \in B$ ， $B \in A$ ；

3) 任意 $B \in B$ ，B是右S-模 $H o m_{R^{o p}} (S, B)$ 的直和项。

则 $G f d_{(F, B)} (M) = G f d_{(F, A)} (M)$ 。

证明由引理2.3知，任意 $(F, B)$ -Gorenstein平坦左S-模都是 $(F, A)$ -Gorenstein平坦左R-模，则 $G f d_{(F, A)} (M) \leq G f d_{(F, B)} (M)$ 。下面证 $G f d_{(F, A)} (M) \geq G f d_{(F, B)} (M)$ ，设 $G f d_{(F, A)} (M) = n < \infty$ ，由引理3.2，只需证对于任意 $B \in B$ 及整数 $i > n$ ， $T o r_{i}^{S} (B, M) = 0$ ，又因对任意 $B \in B$ ， $B \in A$ ，所以 $T o r_{i}^{R} (B, M) = 0$ 。因此 $T o r_{i}^{S} (B \otimes_{R} S, M) ≅ T o r_{i}^{R} (B, M) = 0$ ，另外，由于对任意 $B \in B$ ，B是S-模 $H o m_{R^{o p}} (S, B)$ 的直和项，且 $H o m_{R^{o p}} (S, B) ≅ B \otimes_{R} S$ ，则对任意整数 $i > n$ ， $T o r_{i}^{S} (B, M) = 0$ ，故 $G f d_{(F, B)} (M) \leq n$ 。即 $G f d_{(F, B)} (M) = G f d_{(F, A)} (M)$ 。

命题3.4 若 ${(M_{i})}_{i \in I}$ 是一族左R-模， $G F_{(F, A)}$ 关于扩张封闭， $I (R^{O P}) \subseteq A$ ，则

$G f d_{(F, A)} (\oplus_{I} M_{i}) = \sup {G f d_{(F, A)} (M_{i}) | i \in I}$ 。

证明类似文献 [11] 命题3.11可证。

在定理3.3中，我们需要 $G f d_{(F, B)} (M) < \infty$ ，接下来我们研究在什么情况下，任意左S-模M的 $(F, B)$ -Gorenstein平坦维数沿着环的Frobenius扩张是传递的。

命题3.5 设 $R \subseteq S$ 是环的Frobenius扩张， $G F_{(F, B)}$ 关于扩张封闭， $I (R^{O P}) \subseteq B$ ，假设以下成立

1) 任意 $A \in A$ ， $A \otimes_{R} S \in B$ ；

2) 任意 $B \in B$ ， $B \in A$ ；

3) 任意 $B \in B$ ，B是右S-模 $H o m_{R^{o p}} (S, B)$ 的直和项。

则

a) 若M是左R-模，则 $G f d_{(F, A)} (S \otimes_{R} M) \leq G f d_{(F, B)} (S \otimes_{R} M) \leq G f d_{(F, A)} (M)$ ；

b) 若M作为左S-模，则 $G f d_{(F, A)} (S \otimes_{R} M) = G f d_{(F, B)} (S \otimes_{R} M) = G f d_{(F, A)} (M)$ 。

证明 a)由引理2.3知，任意 $(F, B)$ -Gorenstein平坦左S-模都是 $(F, A)$ -Gorenstein平坦左R-模，则 $G f d_{(F, A)} (S \otimes_{R} M) \leq G f d_{(F, B)} (S \otimes_{R} M)$ 。由引理1.3，易得 $G f d_{(F, B)} (S \otimes_{R} M) \leq G f d_{(F, A)} (M)$ 。

b) 设M是左S-模，则M作为左R-模是 ${}_{R}{(S \otimes_{R} M)}$ 的直和项，由命题3.4，易得 $G f d_{(F, A)} (M) \leq G f d_{(F, A)} (S \otimes_{R} M)$ 。又由(a)知 $G f d_{(F, A)} (S \otimes_{R} M) \leq G f d_{(F, B)} (S \otimes_{R} M) \leq G f d_{(F, A)} (M)$ ，故 $G f d_{(F, A)} (S \otimes_{R} M) = G f d_{(F, B)} (S \otimes_{R} M) = G f d_{(F, A)} (M)$ 。

作为Frobenius代数的推广，2018年，Ren在文献 [8] 中提出了可分Frobenius扩张的概念.

定义3.6 [8] 称 $R \subseteq S$ 是环的可分Frobenius扩张，如果满足以下两条

1) $R \subseteq S$ 是环的可分扩张；

2) $R \subseteq S$ 是环的Frobenius扩张。

称环扩张 $R \subseteq S$ 是可分的，是指乘法映射 $φ : S \otimes_{R} S \to S$ $(s \otimes_{R} l \to s l)$ 是可裂满同态。

定理3.7 设 $R \subseteq S$ 是环的可分Frobenius扩张， $G F_{(F, B)}$ 关于扩张封闭， $I (R^{O P}) \subseteq B$ ，M是任意左S-模，假设以下成立

1) 任意 $A \in A$ ， $A \otimes_{R} S \in B$ ；

2) 任意 $B \in B$ ， $B \in A$ ；

3) 任意 $B \in B$ ，B是S-模 $H o m_{R^{o p}} (S, B)$ 的直和项。

则 $G f d_{(F, B)} (M) = G f d_{(F, A)} (M)$ 。

证明因为 $R \subseteq S$ 是环的可分Frobenius扩张，所以 $φ : S \otimes_{R} M \to M$ $(s \otimes_{R} m \to s m)$ 是可裂满同态，故M是 $S \otimes_{R} M$ 的直和项，由命题3.4，易知 $G f d_{(F, B)} (M) \leq G f d_{(F, B)} (S \otimes_{R} M)$ ，由定理2.7可得不等式 $G f d_{(F, A)} (M) \leq G f d_{(F, B)} (M)$ ，从而由命题3.5(b)，我们有下面的不等式：

$G f d_{(F, B)} (M) = G f d_{(F, A)} (M) = G f d_{(F, A)} (S \otimes_{R} M) = G f d_{(F, B)} (S \otimes_{R} M)$ 。

文章引用

魏玉娟,周彩霞. Frobenius扩张下的(F,A)-Gorenstein平坦模
(F,A)-Gorenstein Flat Modules under Frobenius Extension[J]. 理论数学, 2023, 13(06): 1571-1577. https://doi.org/10.12677/PM.2023.136159

参考文献

1. Overtoun, M., Enochs, E. and Jendan, O. (2011) Relative Homologocal Algebra. DeGruyter, Berlin.

2. Holm, H. and Jorgensen, P. (2009) Cotorsion Pairs Induced by Duality Pairs. Journal of Commutative Algebra, 1, 621-633. https://doi.org/10.1216/JCA-2009-1-4-621

3. Gillespie, J. (2019) Duality and Stable Module Categories. Journal of Pure and Applied Algebra, 223, 3425-3435. https://doi.org/10.1016/j.jpaa.2018.11.010

4. Becerril, V. (2022) -Gorenstein flat homological dimen-sions. Journal of the Korean Mathematical Society, 59, 1203-1227.

5. Kasch, F. (1954) Grundlagen einer Theorie der Frobeniuserweiterungen. Mathematische Annalen, 127, 453-474. https://doi.org/10.1007/BF01361137

6. Nakayama, T. and Tsuzuku, T. (1960) On Frobenius Extensions I. Na-goya Mathematical Journal, 17, 89-110. https://doi.org/10.1017/S0027763000002075

7. Morita, K. (1965) Adjoint Pairs of Functors and Frobenius Ex-tension. Science Reports of the Tokyo Kyoiku Daigaku, Section A, 9, 40-71.

8. Ren, W. (2018) Gorenstein Projective Modules and Frobenius Extensions. Science China Mathematics, 61, 1175-1186. https://doi.org/10.1007/s11425-017-9138-y

9. 任伟. Gorenstein平坦模与Frobenius扩张[J]. 数学学报, 2019, 62(4): 647-652.

10. 张睿杰. Frobenius扩张环上的n-Ding投射模[D]: [硕士学位论文]. 兰州: 西北师范大学, 2020.

11. Holm, H. (2004) Gorenstein Homological Dimensions. Journal of Pure and Applied Algebra, 189, 167-193. https://doi.org/10.1016/j.jpaa.2003.11.007

NOTES

^*第一作者。

期刊菜单