非局部随机扩散方程解的H?lder连续性 H?lder Continuous of the Solutions to Nonlocal Stochastic Diffusion Equations

doi:10.12677/PM.2023.1312351

Pure Mathematics
Vol. 13 No. 12 ( 2023 ), Article ID: 77505 , 15 pages
10.12677/PM.2023.1312351

非局部随机扩散方程解的Hölder连续性

贾倩^*，王伟

●How to Cite this Article

天津师范大学数学科学学院，天津

收稿日期：2023年11月7日；录用日期：2023年12月7日；发布日期：2023年12月18日

摘要

本文的目标是获得非局部随机扩散方程解的Hölder连续性。利用Campanato估计和Sobolev嵌入定理，首先证明了非局部随机扩散方程的温和解的Hölder连续性，即解u属于空间 $C^{β} (D_{T}; L^{p} (Ω))$ 。其次，通过使用尾估计，得到了 $L^{p} (Ω; C^{β^{*}} (D_{T}))$ 中的温和解的估计。

关键词

分数布朗运动，Hölder连续性， $L^{\infty}$ 估计，尾估计

Hölder Continuous of the Solutions to Nonlocal Stochastic Diffusion Equations

Qian Jia^*, Wei Wang

College of Mathematical Sciences, Tianjin Normal University, Tianjin

Received: Nov. 7^th, 2023; accepted: Dec. 7^th, 2023; published: Dec. 18^th, 2023

ABSTRACT

In this paper, we aim to obtain the Hölder continuous of solutions to nonlocal stochastic equations. By using Campanato estimates and Sobolev embedding theorem, we first prove the Hölder continuous of the mild solution of nonlocalstochastic diffusion equations in the sense that the solution u belongs to the space $C^{β} (D_{T}; L^{p} (Ω))$ . Then by using tail estimates, we obtain the estimates of the mild solution in $L^{p} (Ω; C^{β^{*}} (D_{T}))$ .

Keywords:Fractional Brownian Motion, Hölder Continuity, $L^{\infty}$ Estimates, Tail Estimates

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

设 $T > 0$ ， $D \subset ℝ$ 并且 $D_{T} : = [0, T] \times D$ 。设 ${Ω, F, {F}_{t \geq 0}, ℙ}$ 是一个给定的过滤概率空间。文章 [1] [2] 获得了 $L^{p, θ} ((D_{T}; δ); L^{p} (ℝ))$ 空间(见定义2.1)的奇异随机积分的正则性，其中 $p > 1, θ > 0, δ > 0$ 。进一步，借助Sobolev嵌入定理对于任意的 $θ > 1$ ， $L^{p, θ} (D; δ) \mapsto C^{γ} (D_{T}; L^{P} (Ω))$ ，获得了在Hölder空间 $C^{γ} (D_{T}; L^{p} (Ω))$ ( $γ = \frac{3 (θ - 1)}{p}$ )中解的估计。本文的目标是得到 $L^{p} (Ω; C^{β} (D_{T}))$ ( $β = \frac{3 (θ - 1)}{p}$ )中解的估计，我们考虑如下方程

$d u_{t} = Δ^{α} u d t + g (t, x) d B_{t}^{ℏ}, {u |}_{t = 0} = 0,$ (1)

其中 $Δ^{α} = - {(- Δ)}^{α}$ ， $B_{t}^{ℏ}$ 为具有Hurst参数 $ℏ \in (0, \frac{1}{2})$ 的一维分数布朗运动。设方程(1)的mild解记为

$K g (t, x) : = \int_{0}^{t} \int_{ℝ} K (t - r, y) g (r, x - y) d y d B^{ℏ} (t) .$

非局部扩散方程的起源可以追溯到1899年分子间作用力的发现，分子间作用力的发现打破了牛顿的传统力学体系。于是，物理学上的突破也引申到数学上，与牛顿力学体系对应的是我们熟知的局部扩散方程。而与分子间作用力对应的方程是非局部扩散方程，作为微分方程的重要分支，非局部扩散方程从20世纪70年代才开始逐步发展并且成熟起来。非局部扩散方程比很多其他方程有更广泛的应用，渗透在生物模型，化学反应模型，物理模型等各个方面。

让我们首先回顾一下关于随机偏微分方程(SPDE)解的正则性的相关结论。与确定性抛物方程一样，随机偏微分方程的正则性研究主要包括两个部分：一个是L_p理论，另一个是Schauder理论(Hölder连续估计)。关于L_p理论的最早结果出现在Krylov的 [3] [4] 中。Kim-Kim [5] 考虑了由Lévy过程驱动的随机偏微分方程的L_p理论。Zhang [6] 获得了一般测度空间上半线性随机偏微分方程的L_p理论并且 [7] 证明了确定性非局部抛物偏微分方程的L_p极大正则性和Cauchy过程驱动的随机微分方程的Krylov估计。

分数布朗运动出现在许多复杂现象模型的应用中。当分数布朗运动的Hurst参数 $ℏ = \frac{1}{2}$ 时，分数布朗运动成为标准布朗运动。分数布朗运动与标准布朗运动的不同之处在于分数布朗运动缺少半鞅性、马尔可夫性和其他经典的随机过程理论 [8] 。分数布朗运动作为一个中心高斯过程，它的特点是其增量的平稳性和中或长记忆的性质。长记忆特性使分数布朗运动成为许多领域建模的候选者 [9] 。对于与分数布朗运动有关的数学模型是近年来的研究热点。如Boufoussi和Hajji [10] 研究了由分数布朗运动驱动的中立型随机泛函微分方程解的存在唯一性和指数渐近行为；Caraball等 [11] 研究了具有分数布朗运动驱动的随机延迟演化方程解的存在性和指数行为；Li和Yan [12] 讨论了在希尔伯特空间上由分数布朗运动驱动的一类中立随机泛函微分方程的遍历性和平稳解；Xu等 [13] 讨论了由分数布朗运动驱动的二阶中立型随机泛函微分方程的全局吸引集和指数衰减。

许多作者对随机偏微分方程的Hölder估计越来越感兴趣。Hsu等 [14] 建立了半线性随机偏微分方程的随机De Giorgi迭代和正则性。Du和Liu [15] 获得了随机偏微分方程解的Schauder估计。结合确定性理论和卷积性质，Debussche等 [16] 建立了抛物型拟线性随机偏微分方程的正则性结果。Kuksin等 [17] 获得了有界域上抛物型随机偏微分方程解的Hölder估计。最近，Tian等 [18] 利用尾估计获得了非局部随机扩散方程温和解的Hölder估计。论文 [19] 考虑了由布朗运动驱动的非局部随机抛物型偏微分方程的正则性。本文旨在将 [19] 的结果推广到由Hurst参数 $ℏ \in (0, 1 / 2)$ 的分数布朗运动驱动的抛物型非局部随机偏微分方程的正则性。

2. 预备知识

假设对于 $X = (t, x) \in ℝ \times ℝ$ ， $Y = (s, y) \in ℝ \times ℝ$ ，有

$δ (X, Y) : = \max {| x - y |, {| t - s |}^{\frac{1}{2}}} .$

假设 $Q_{c} (X)$ 是一个以 $X = (t, x)$ 为圆心， $c > 0$ 为半径的球，即

$Q_{c} (X) : = {Y = (s, y) \in ℝ \times ℝ : δ (X, Y) < c} = (t - c^{2}, t + c^{2}) \times B_{c} (x) .$

固定任意的 $T \in (0, \infty)$ ， $O_{T} : = (0, T) \times ℝ$ 表示一个光滑的区域。设D是一个有界区域 $D \in ℝ$ ，对于一个点 $X \in D_{T}$ ， $D (X, r) : = D_{T} \cap Q_{r} (X)$ 并且 $d (D) = d i a m (D)$ 。我们首先介绍Campanato空间的定义。

定义2.1 [20] 设 $p \geq 1$ ， $θ \geq 0$ 。如果一个函数u满足

${[u]}_{L^{p, θ} (D_{T}; δ)} = {(\sup_{X \in D_{T}, d (D) \geq ρ > 0} \frac{1}{{| D (X, c) |}^{θ}} {\int_{D (X, ρ)} | u (Y) - u_{X, ρ} |}^{p} d Y)}^{\frac{1}{p}} < \infty, u \in L^{p} (D_{T}),$

其中 $| D (X, ρ) |$ 表示Borel集 $D (X, ρ)$ 的Lebesgue测度并且

$u_{X, ρ} : = \frac{1}{D (X, ρ)} \int_{D (X, ρ)} u (Y) d Y,$

则称u属于Campanato空间 $L^{p, θ} (D; δ)$ ，该空间为 $L^{p} (D)$ 的子空间。对于 $u \in L^{p, θ} (D_{T}; δ)$ ，定义

${‖ u ‖}_{L^{p, θ} (D_{T}; δ)} : = {({‖ u ‖}_{L^{p} {(D_{T})}^{p}} + {[u]}_{L^{p, θ} (D_{T}; δ)})}^{\frac{1}{p}} .$

定义2.2 [19] 设 $0 < γ \leq 1$ ，如果函数u满足

${[u]}_{C^{γ} ({\bar{D}}_{T}; δ)} : = \sup_{X \in D_{T}, d (D) \geq ρ > 0} \frac{| u (X) - u (Y) |}{δ {(X, Y)}^{γ}} < \infty,$

则称u属于Hölder空间 $C^{γ} ({\bar{D}}_{T}; δ)$ 。对于 $u \in C^{γ} ({\bar{D}}_{T}; δ)$ ，定义

${‖ u ‖}_{C^{γ} ({\bar{D}}_{T}; δ)} : = \sup_{D_{T}} | u | + {[u]}_{C^{γ} ({\bar{D}}_{T}; δ)} .$

定义2.3 设 $D_{T} \subset ℝ$ 是一个域，如果存在 $A > 0$ 使得对于任意的 $X \in D_{T}$ ， $0 < ρ \leq d (D)$ ，使得 $| D_{T} (X, ρ) | = | D_{T} \cap Q_{ρ} (X) | \geq A | Q_{ρ} (X) |$ ，那么域 $D_{T}$ 叫做A-类。

下面是一些符号说明。

给定两个集合 $B_{1}$ 和 $B_{2}$ ，关系 $B_{1} = B_{2}$ 意味着 $B_{1} \subset B_{2}$ 并且 $B_{2} \subset B_{1}$ 。符号 $f (x) \approx g (x)$ 表示有一个独立于x的数字 $0 < C < \infty$ ，即一个常数，这样对于每个x，我们都有 $C^{- 1} f (x) \leq g (x) \leq C f (x)$ 。然后我们有下面关于上面定义的两个空间的比较的关系。

命题2.4 设 $D_{T}$ 是一个有界区域，则对于任意 $p \geq 1$ 和 $1 < θ < 1 + \frac{p}{3}$ ，有 $L^{p, θ} (D_{T}; δ) ≅ C^{γ} ({\bar{D}}_{T}; δ)$ ，其中 $γ = \frac{3 (θ - 1)}{p}$ 。

我们想用尾估计来得到随机偏微分方程的解u的有界性结果

$E {‖ u ‖}_{C^{γ} ([0, T) \times D)}^{p} \leq C, p \geq 1.$

将使用尾估计和Hölder空间与Campanato空间之间的等价，事实上对于任意常数 $M > 0$ ，

$\begin{matrix} E ({| X |}^{p}) = \int_{Ω} {| X |}^{p} d ℙ (ω) \\ = p \int_{0}^{\infty} ℙ {| X | > a} a^{p - 1} d a \\ = p \int_{0}^{M} ℙ {| X | > a} a^{p - 1} d a + p \int_{M}^{\infty} ℙ {| X | > a} a^{p - 1} d a \\ \leq M^{P} + p \int_{M}^{\infty} ℙ {| X | > a} a^{p - 1} d a, \end{matrix}$

为了得到 $L^{p}$ 有界性，根据上面的不等式，我们只需要证明第二个积分是有界的。

命题2.5 [21] 设 $u_{0} \in L^{p} (ℝ, Ω)$ 。考虑柯西问题

$\partial_{t} u (t, x) = Δ^{α} u (t, x), t > 0, x \in ℝ; u (0, x) = u_{0} (x),$ (2)

那么对于任意的 $0 < β < 1$ ， ${‖ u (t, \cdot) ‖}_{C^{β} (ℝ)} \leq C t^{- \frac{β}{2 α} - \frac{1}{2 p α}} {‖ u_{0} ‖}_{L^{p} (ℝ)}$ ，并且对于任意的 $τ > 0$ ， $| u (t + τ, x) - u (t, x) | \leq C t^{- β - \frac{1}{2 p α}} τ^{β} {‖ u_{0} ‖}_{L^{p} (ℝ)}$ 。

我们回顾一些满足 $K_{t} = Δ^{α} K$ 的核函数 $K (t, x, y)$ 的一些性质(参见 [21] [22] [23] [24] )。

1) 对于任意的 $t > 0$ ， ${‖ K (t, \cdot) ‖}_{L^{1} (ℝ)} = 1$ ；

2) 对于每一个 $t > 0$ ， $K (t, x, y)$ 在区间 $(, \infty)$ 中属于 $C^{\infty}$ ；

3)对于任意的 $t > 0$ ， $x, y \in ℝ$ ， $x \neq y$ ， $K (t, x)$ 的渐进估计为 $| \nabla_{x} K (t, x, y) | \approx | y - x | \min {\frac{t}{{| y - x |}^{5}}, t^{- \frac{3}{2}}}$ 。

最后，我们介绍关于分数布朗运动的维纳积分的一些基本结果。设 ${Ω, F, ℙ, {F}_{t \geq 0}}$ 是一个过滤概率空间。假设 $B^{ℏ} (t)$ ， $t \in [0, T]$ 是具有Hurst参数 $ℏ \in (0, \frac{1}{2})$ 的一维分数布朗运动。这意味着 $B^{ℏ}$ 是一个中心高斯过程，协方差函数为

$R_{ℏ} (t, s) = E (B_{t}^{ℏ} B_{s}^{ℏ}) = \frac{1}{2} (t^{2 ℏ} + s^{2 ℏ} - {| t - s |}^{2 ℏ}),$

考虑核

$K_{ℏ} (t, s) = c_{ℏ} [{(\frac{t}{s})}^{ℏ - \frac{1}{2}} {(t - s)}^{ℏ - \frac{1}{2}} - (ℏ - \frac{1}{2}) s^{\frac{1}{2} - ℏ} \int_{s}^{t} {(u - s)}^{ℏ - \frac{1}{2}} u^{ℏ - \frac{3}{2}} d u], 0 < ℏ < \frac{1}{2}, t > s,$

其中 $c_{ℏ} = \sqrt{\frac{ℏ}{(1 - 2 ℏ) β (1 - 2 ℏ, ℏ + \frac{1}{2})}}$ ， $β (\cdot, \cdot)$ 表示Beta函数。如果 $t \leq s$ ，则 $K_{ℏ} (t, s) = 0$ 。由上式可知

$| K_{ℏ} (t, s) | \leq 2 c_{ℏ} ({(t - s)}^{ℏ - \frac{1}{2}} + s^{ℏ - \frac{1}{2}}) .$ (3)

由 [25] 知，

$| \frac{\partial K_{ℏ}}{\partial t} (t, s) | \leq c_{ℏ} (\frac{1}{2} - ℏ) {(t - s)}^{ℏ - \frac{3}{2}} .$ (4)

考虑从 $H$ 到 $L^{2} ([0, T])$ 的算子 $K_{ℏ, T}^{*}$ [13] ，

$(K_{ℏ, T}^{*} φ) (s) = K_{ℏ} (T, s) φ (s) + \int_{s}^{T} (φ (r) - φ (s)) \frac{\partial K_{ℏ}}{\partial r} (r, s) d r,$ (5)

则 $K_{ℏ, T}^{*}$ 是一个 $H$ 和 $L^{2} ([0, T])$ 之间的等距算子。

考虑 $W = {W_{t}, t \in [0, T]}$ ，定义 $W_{t} = B^{ℏ} ({(K_{ℏ}^{*})}^{- 1} (1_{[0, 1]}))$ ，则W是一个维纳过程，并且过程 $B^{ℏ}$ 有积分表示 $B^{ℏ} (t) = \int_{0}^{t} K_{ℏ} (t, s) d W (s)$ 。此外，对于任何一个 $φ \in H$ ，我们都有

$\int_{0}^{T} φ (s) d B^{ℏ} (s) = \int_{0}^{T} (K_{ℏ}^{*} φ) (t) d W (t) .$ (6)

3. Hölder估计

本文的假设如下：

(H1)对于任意的 $t, s \in [0, T]$ ， $z \in ℝ$ 且 $q > 1$ ，有 $\int_{ℝ} {| K (t, z) - K (s, z) |}^{q} d z \leq {(t - s)}^{q γ_{1}}$ ，其中 $γ_{1}$ 为一个依赖于q的常数。

(H2)对于任意的 $t, s \in [0, T]$ ， $z \in ℝ$ 且 $p > 1$ ，有 $\int_{ℝ} {| g (t, z) - g (s, z) |}^{p} d z \leq {(t - s)}^{p γ_{2}}$ ，其中 $γ_{2}$ 为一个依赖于p的常数。

定理3.1设D是一个A-类有界域使得 $\bar{D} \subset O_{T}$ 。假设对于 $p > \frac{1}{α}$ ， $g \in L_{l o c}^{\infty} (ℝ_{+}; L^{p} (Ω \times ℝ))$ 是一个 $F_{t}$ 适应过程， $0 < β < α$ 且 $(α - β) p - 1 \geq 0$ 。(H1)和(H2)成立。则方程(1)存在mild解u，使得 $u \in L^{p, θ} ((D_{T}; δ); L^{p} (Ω)) \cap L^{p} (Ω; C^{β} (D_{T}))$ ，且

${‖ u ‖}_{L^{p, θ} ((D_{T}; δ); L^{p} (Ω))} \leq C {‖ g ‖}_{L^{\infty} ([0, T]; L^{p} (Ω \times ℝ))},$ (7)

${‖ u ‖}_{C^{β} (D_{T}; L^{p} (Ω))} \leq C {‖ g ‖}_{L^{\infty} ([0, T]; L^{p} (Ω \times ℝ))},$ (8)

其中 $θ = 1 + \frac{β p}{3}$ 。进一步，取 $0 < ϵ < \frac{β p}{2}$ ， $q > \frac{3}{ϵ}$ ，对于任意的 $1 < r < q$ ，

${‖ u ‖}_{L^{r} (Ω; C^{β^{*}} (D_{T}))} \leq C {‖ g ‖}_{L^{\infty} ([0, T]; L^{p q} (Ω \times ℝ))},$ (9)

其中 $β^{*} = β - \frac{2 ϵ}{p}$ 。

证明：在上述假设下方程(1)温和解的存在性是一个经典结果。现在我们证明不等式(7)。由于Campanato空间的定义，只需证明 ${[u]}_{L^{p, θ} ((D_{T}; δ); L^{p} (Ω))}^{p} < \infty$ 。

首先，根据定义2.1有，

$\begin{matrix} {[u]}_{L^{p, θ} ((D_{T}; δ); L^{p} (Ω))}^{p} \leq \sup_{D (X, c), X \in D_{T}, 0 < c \leq d (D)} \frac{1}{{| D (X, c) |}^{1 + θ}} E \int_{D (X, c)} \int_{D (X, c)} {| u (t, x) - u (s, y) |}^{p} d t d x d s d y \\ \leq \sup_{D (X, c), X \in D_{T}, 0 < c \leq d (D)} \frac{1}{{| D (X, c) |}^{1 + θ}} E \int_{D (X, c)} \int_{D (X, c)} | \int_{0}^{t} \int_{ℝ} K (t - r, x - z) g (r, z) d z d B^{ℏ} (r) \\ {- \int_{0}^{s} \int_{ℝ} K (s - r, y - z) g (r, z) d z d B^{ℏ} (r) |}^{p} d t d x d s d y \\ : = \sup_{D (X, c), X \in D_{T}, 0 < c \leq d (D)} \frac{1}{{| D (X, c) |}^{1 + θ}} \int_{D (X, c)} \int_{D (X, c)} E Υ d t d x d s d y . \end{matrix}$

由公式(5)和(6)，有

$\begin{matrix} E Υ \leq 2^{p - 1} {| \int_{0}^{s} \int_{ℝ} (K (t - r, x - z) - K (s - r, y - z)) g (r, z) d z d B^{ℏ} (r) |}^{p} \\ + 2^{p - 1} {| \int_{s}^{t} \int_{ℝ} K (s - r, y - z) g (r, z) d z d B^{ℏ} (r) |}^{p} \\ \leq 2^{p - 1} {| \int_{0}^{s} K_{ℏ}^{*} [\int_{ℝ} (K (t - r, x - z) - K (s - r, y - z)) g (r, z) d z] (r) d W (r) |}^{p} \\ + 2^{p - 1} {| \int_{s}^{t} K_{ℏ}^{*} [\int_{ℝ} K (s - r, y - z) g (r, z) d z] (r) d W (r) |}^{p} \end{matrix}$

$\begin{matrix} \leq 2^{p - 1} | \int_{0}^{s} [K_{ℏ} (s, r) \int_{ℝ} (K (t - r, x - z) - K (s - r, y - z)) g (r, z) d z (r) \overset{}{} \\ + \int_{r}^{s} [\int_{ℝ} (K (t - m, x - z) - K (s - m, y - z)) g (m, z) d z (r) \\ - \int_{ℝ} (K (t - r, x - z) - K (s - r, y - z)) g (r, z) d z (r)] {\frac{\partial K_{ℏ}}{\partial m} (m, r) d m] d W (r) |}^{p} \\ + 2^{p - 1} | \int_{s}^{t} [K_{ℏ} (t, r) \int_{ℝ} K (s - r, y - z) g (r, z) d z \overset{}{} \\ + {\int_{r}^{t} [\int_{ℝ} K (t - m, x - z) g (m, z) d z - \int_{ℝ} K (t - r, x - z) g (r, z) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m] d W (r) |}^{p} \end{matrix}$

$\begin{matrix} \leq 2^{2 p - 2} {| \int_{0}^{s} K_{ℏ} (s, r) \int_{ℝ} (K (t - r, x - z) - K (s - r, y - z)) g (r, z) d z (r) d W (r) |}^{p} \\ + 2^{2 p - 2} | \int_{0}^{s} \int_{r}^{s} [\int_{ℝ} (K (t - m, x - z) - K (s - m, y - z)) g (m, z) d z \\ - {\int_{ℝ} (K (t - r, x - z) - K (s - r, y - z)) g (r, z) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m d W (r) |}^{p} \\ + 2^{2 p - 2} {| \int_{s}^{t} K_{ℏ} (t, r) \int_{ℝ} K (s - r, y - z) g (r, z) d z d W (r) |}^{p} \\ + 2^{2 p - 2} {| \int_{s}^{t} \int_{r}^{t} [\int_{ℝ} K (t - m, x - z) g (m, z) d z - \int_{ℝ} K (t - r, x - z) g (r, z) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m d W (r) |}^{p} \end{matrix}$

$\begin{matrix} = 2^{2 p - 2} {| \int_{0}^{s} K_{ℏ} (s, r) \int_{ℝ} (K (t - r, x - z) - K (s - r, y - z)) g (r, z) d z (r) d W (r) |}^{p} \\ + 2^{2 p - 2} | \int_{0}^{s} \int_{r}^{s} [\int_{ℝ} K (t - m, x - z) g (m, z) - K (t - r, x - z) g (r, z) d z \\ + {\int_{ℝ} K (s - r, y - z) g (r, z) - K (s - m, y - z) g (m, z) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m d W (r) |}^{p} \end{matrix}$

$\begin{matrix} + 2^{2 p - 2} {| \int_{s}^{t} K_{ℏ} (t, r) \int_{ℝ} K (s - r, y - z) g (r, z) d z d W (r) |}^{p} \\ + 2^{2 p - 2} {| \int_{s}^{t} \int_{r}^{t} [\int_{ℝ} K (t - m, x - z) g (m, z) d z - \int_{ℝ} K (t - r, x - z) g (r, z) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m d W (r) |}^{p} \end{matrix}$

$\begin{matrix} = C_{1} {| \int_{0}^{s} {[K_{ℏ} (s, r) \int_{ℝ} (K (t - r, x - z) - K (s - r, y - z)) g (r, z) d z (r)]}^{2} d r |}^{\frac{p}{2}} \\ + C_{1} | \int_{0}^{s} [\int_{r}^{s} [\int_{ℝ} K (t - m, x - z) g (m, z) - K (t - r, x - z) g (r, z) d z \\ {+ {\int_{ℝ} K (s - r, y - z) g (r, z) - K (s - m, y - z) g (m, z) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m]}^{2} d r |}^{\frac{p}{2}} \\ + C_{1} {| \int_{s}^{t} {[K_{ℏ} (t, r) \int_{ℝ} K (s - r, y - z) g (r, z) d z]}^{2} d r |}^{\frac{p}{2}} \\ + C_{1} {| \int_{s}^{t} {[\int_{r}^{t} [\int_{ℝ} K (t - m, x - z) g (m, z) d z - \int_{ℝ} K (t - r, x - z) g (r, z) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m]}^{2} d r |}^{\frac{p}{2}} \\ : = C_{1} (H_{1} + H_{2} + H_{3} + H_{4}), \end{matrix}$

其中C₁为一个常数。下面，分别估计H₁，H₂，H₃，H₄。利用不等式(3)和假设(H1)，有

$\begin{matrix} H_{1} = {| \int_{0}^{s} {[K_{ℏ} (s, r) \int_{ℝ} (K (t - r, x - z) - K (s - r, y - z)) g (r, z) d z (r)]}^{2} d r |}^{\frac{p}{2}} \\ \leq 2^{\frac{p}{2}} {| \int_{0}^{s} {| K_{ℏ} (s, r) |}^{2} {[\int_{ℝ} | K (t - r, x - z) - K (s - r, x - z) | \cdot | g (r, z) | d z (r)]}^{2} d r |}^{\frac{p}{2}} \\ + 2^{\frac{p}{2}} {| \int_{0}^{s} {| K_{ℏ} (s, r) |}^{2} {[\int_{ℝ} | K (s - r, x - z) - K (s - r, y - z) | \cdot | g (r, z) | d z (r)]}^{2} d r |}^{\frac{p}{2}} \\ \leq 2^{\frac{p}{2}} {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} {| \int_{0}^{s} {| K_{ℏ} (s, r) |}^{2} {[{\int_{ℝ} | K (t - r, x - z) - K (s - r, x - z) |}^{q} d z (r)]}^{\frac{2}{q}} d r |}^{\frac{p}{2}} \\ + 2^{\frac{p}{2}} {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} {| \int_{0}^{s} {| K_{ℏ} (s, r) |}^{2} {[{\int_{ℝ} | K (s - r, x - z) - K (s - r, y - z) |}^{q} d z (r)]}^{\frac{2}{q}} d r |}^{\frac{p}{2}} \end{matrix}$

$\begin{matrix} \leq 2^{2 p} {(C_{ℏ})}^{p} C {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} {| \int_{0}^{s} [{(s - r)}^{2 ℏ - 1} + r^{2 ℏ - 1}] {(t - s)}^{2 γ_{1}} d r |}^{\frac{p}{2}} \\ + 2^{2 p} {(C_{ℏ})}^{p} C {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} {| x - y |}^{β p} {| \int_{0}^{s} {(s - r)}^{- \frac{β}{α} - \frac{1}{p α}} [{(s - r)}^{2 ℏ - 1} + r^{2 ℏ - 1}] d r |}^{\frac{p}{2}} \\ = 2^{2 p} {(C_{ℏ})}^{p} C {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} ℏ^{- \frac{p}{2}} s^{ℏ p} {(t - s)}^{γ_{1} p} \\ + 2^{2 p} {(C_{ℏ})}^{p} C {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} {| x - y |}^{β p} {| \frac{1}{- \frac{β}{α} - \frac{1}{p α} + 2 ℏ} s^{- \frac{β}{α} - \frac{1}{p α} + 2 ℏ} + β (1 - \frac{β}{α} - \frac{1}{p α}, 2 ℏ) s^{- \frac{β}{α} - \frac{1}{p α} + 2 ℏ} |}^{\frac{p}{2}} . \end{matrix}$

根据假设(H1)，(H2)和公式(4)，有

$\begin{matrix} H_{2} = | \int_{0}^{s} [\int_{r}^{s} [\int_{ℝ} K (t - m, x - z) g (m, z) - K (t - r, x - z) g (r, z) d z \\ + {{\int_{ℝ} K (s - r, y - z) g (r, z) - K (s - m, y - z) g (m, z) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m]}^{2} d r |}^{\frac{p}{2}} \\ \leq 2^{\frac{p}{2}} | {\int_{0}^{s} [\int_{r}^{s} [\int_{ℝ} K (t - m, x - z) g (m, z) - K (t - r, x - z) g (r, z) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m]}^{2} d r \\ + {{\int_{0}^{s} [\int_{r}^{s} [\int_{ℝ} K (s - r, y - z) g (r, z) - K (s - m, y - z) g (m, z) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m]}^{2} d r |}^{\frac{p}{2}} \end{matrix}$

$\begin{matrix} \leq 2^{p} | {\int_{0}^{s} [\int_{r}^{s} [\int_{ℝ} (K (t - m, x - z) - K (t - r, x - z)) g (m, z) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m]}^{2} d r \\ + {\int_{0}^{s} [\int_{r}^{s} [\int_{ℝ} K (t - r, x - z) (g (m, z) - g (r, z)) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m]}^{2} d r \\ + {\int_{0}^{s} [\int_{r}^{s} [\int_{ℝ} (K (s - r, y - z) - K (s - m, y - z)) g (r, z) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m]}^{2} d r \\ + {{\int_{0}^{s} [\int_{r}^{s} [\int_{ℝ} K (s - m, y - z) (g (r, z) - g (m, z)) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m]}^{2} d r |}^{\frac{p}{2}} \end{matrix}$

$\begin{matrix} \leq 2^{p} | {\int_{0}^{s} [\int_{r}^{s} [\int_{ℝ} | K (t - r, x - z) - K (t - m, x - z) | \cdot | g (m, z) | d z] | \frac{\partial K_{ℏ}}{\partial m} (m, r) | d m]}^{2} d r \\ + {\int_{0}^{s} [\int_{r}^{s} [\int_{ℝ} | K (t - r, x - z) | \cdot | g (m, z) - g (r, z) | d z] | \frac{\partial K_{ℏ}}{\partial m} (m, r) | d m]}^{2} d r \\ + {\int_{0}^{s} [\int_{r}^{s} [\int_{ℝ} | K (s - r, y - z) - K (s - m, y - z) | \cdot | g (r, z) | d z] | \frac{\partial K_{ℏ}}{\partial m} (m, r) | d m]}^{2} d r \\ + {{\int_{0}^{s} [\int_{r}^{s} [\int_{ℝ} | K (s - m, y - z) | \cdot | g (m, z) - g (r, z) | d z] | \frac{\partial K_{ℏ}}{\partial m} (m, r) | d m]}^{2} d r |}^{\frac{p}{2}} \end{matrix}$

$\begin{matrix} \leq 2^{p} {(C_{ℏ})}^{p} | {\int_{0}^{s} [{\int_{r}^{s} [\int_{ℝ} {| K (t - r, x - z) - K (t - m, x - z) |}^{q} | g (m, z) | d z]}^{\frac{1}{q}} {(m - r)}^{ℏ - \frac{3}{2}} d m]}^{2} d r {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{2} \\ + {\int_{0}^{s} [{\int_{r}^{s} [\int_{ℝ} {| K (t - r, x - z) |}^{q} d z]}^{\frac{1}{q}} {[\int_{ℝ} {| g (m, z) - g (r, z) |}^{p} d z]}^{\frac{1}{p}} d m {(m - r)}^{ℏ - \frac{3}{2}}]}^{2} d r \\ + {\int_{0}^{s} [\int_{r}^{s} {[\int_{ℝ} {| K (s - r, y - z) - K (s - m, y - z) |}^{q} | g (r, z) | d z]}^{\frac{1}{q}} {(m - r)}^{ℏ - \frac{3}{2}} d m]}^{2} d r {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{2} \\ + {{\int_{0}^{s} [\int_{r}^{s} {[\int_{ℝ} {| K (s - m, y - z) |}^{q} d z]}^{\frac{1}{q}} {[\int_{ℝ} {| g (m, z) - g (r, z) |}^{p} d z]}^{\frac{1}{p}} {(m - r)}^{ℏ - \frac{3}{2}} d m]}^{2} d r |}^{\frac{p}{2}} \end{matrix}$

$\begin{matrix} = 2^{p} {(C_{ℏ})}^{p} {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} | \frac{1}{{(ℏ + γ_{1} - \frac{1}{2})}^{2} (2 ℏ + 2 γ_{1})} s^{2 ℏ + 2 γ_{1}} + \int_{0}^{s} \frac{1}{ℏ + γ_{2} - \frac{1}{2}} {(t - r)}^{\frac{q α - (p - 1)}{2 q α}} {(s - r)}^{ℏ + γ_{2} - \frac{1}{2}} d r \\ {+ \frac{1}{{(ℏ + γ_{1} - \frac{1}{2})}^{2} (2 ℏ + 2 γ_{1})} s^{2 ℏ + 2 γ_{1}} + \int_{0}^{s} β (\frac{3 q α - (p - 1)}{2 q α}, ℏ + γ_{2} - \frac{1}{2}) {(s - r)}^{\frac{q α - (p - 1)}{2 q α} + ℏ + γ_{2} - \frac{1}{2}} d r |}^{\frac{p}{2}} \\ \leq 2^{p} {(C_{ℏ})}^{p} {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} | \frac{1}{{(ℏ + γ_{1} - \frac{1}{2})}^{2} (2 ℏ + 2 γ_{1})} s^{2 ℏ + 2 γ_{1}} + \int_{0}^{t} \frac{1}{ℏ + γ_{2} - \frac{1}{2}} {(t - r)}^{\frac{q α - (p - 1)}{2 q α} + ℏ + γ_{2} - \frac{1}{2}} d r \\ {+ \frac{1}{{(ℏ + γ_{1} - \frac{1}{2})}^{2} (2 ℏ + 2 γ_{1})} s^{2 ℏ + 2 γ_{1}} + \int_{0}^{s} β (\frac{3 q α - (p - 1)}{2 q α}, ℏ + γ_{2} - \frac{1}{2}) {(s - r)}^{\frac{q α - (p - 1)}{2 q α} + ℏ + γ_{2} - \frac{1}{2}} d r |}^{\frac{p}{2}} \end{matrix}$

$\begin{matrix} \leq 2^{p} {(C_{ℏ})}^{p} {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} | \frac{1}{{(ℏ + γ_{1} - \frac{1}{2})}^{2} (2 ℏ + 2 γ_{1})} s^{2 ℏ + 2 γ_{1}} \\ + \frac{1}{ℏ + γ_{2} - \frac{1}{2}} \frac{1}{\frac{q α - (p - 1)}{2 q α} + ℏ + γ_{2} + \frac{1}{2}} t^{\frac{q α - (p - 1)}{2 q α} + ℏ + γ_{2} + \frac{1}{2}} + \frac{1}{{(ℏ + γ_{1} - \frac{1}{2})}^{2} (2 ℏ + 2 γ_{1})} s^{2 ℏ + 2 γ_{1}} \\ + {β (\frac{3 q α - (p - 1)}{2 q α}, ℏ + γ_{2} - \frac{1}{2}) \frac{1}{\frac{q α - (p - 1)}{2 q α} + ℏ + γ_{2} + \frac{1}{2}} s^{\frac{q α - (p - 1)}{2 q α} + ℏ + γ_{2} + \frac{1}{2}} |}^{\frac{p}{2}}, \end{matrix}$

其中 $q = \frac{p}{p - 1}$ 。因为 $α p > 1$ ，所以 $q α - (p - 1) > 0$ 。由公式(3)有

$\begin{matrix} H_{3} = {| \int_{s}^{t} {[K_{ℏ} (t, r) \int_{ℝ} K (s - r, y - z) g (r, z) d z]}^{2} d r |}^{\frac{p}{2}} \\ \leq {| \int_{s}^{t} {| K_{ℏ} (t, r) |}^{2} {[\int_{ℝ} | K (s - r, y - z) | \cdot | g (r, z) | d z]}^{2} d r |}^{\frac{p}{2}} \\ \leq {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} {| \int_{s}^{t} {| K_{ℏ} (t, r) |}^{2} {[\int_{ℝ} {| K (s - r, y - z) |}^{q} d z]}^{\frac{2}{q}} d r |}^{\frac{p}{2}} \\ \leq 2^{2 p} {(C_{ℏ})}^{p} {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} {| \int_{s}^{t} ({(t - r)}^{2 ℏ - 1} + r^{2 ℏ - 1}) {(t - r)}^{\frac{2 q α - (q - 1)}{q α}} d r |}^{\frac{p}{2}} \end{matrix}$

$\leq 2^{2 p} {(C_{ℏ})}^{p} {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} {| \frac{1}{\frac{2 q α - (q - 1)}{q α} + 2 ℏ} {(t - s)}^{\frac{2 q α - (q - 1)}{q α} + 2 ℏ} + β (2 ℏ, \frac{3 q α - (q - 1)}{q α}) t^{\frac{2 q α - (q - 1)}{q α} + 2 ℏ} |}^{\frac{p}{2}} .$

利用假设(H1)和公式(4)，有

$\begin{matrix} H_{4} = {| \int_{s}^{t} {[\int_{r}^{t} [\int_{ℝ} K (t - m, x - z) g (m, z) - K (t - r, x - z) g (r, z) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m]}^{2} d r |}^{\frac{p}{2}} \\ \leq 2^{p} | {\int_{s}^{t} [\int_{r}^{t} [\int_{ℝ} (K (t - m, x - z) - K (t - r, x - z)) g (m, z) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m]}^{2} d r \\ + {{\int_{s}^{t} [\int_{r}^{t} [\int_{ℝ} K (t - r, x - z) (g (m, z) - g (r, z)) d z] \frac{\partial K_{ℏ}}{\partial m} (m, r) d m]}^{2} d r |}^{\frac{p}{2}} \\ \leq 2^{p} | \int_{s}^{t} {[\int_{r}^{t} [\int_{ℝ} | K (t - r, x - z) - K (t - m, x - z) | \cdot | g (m, z) | d z] | \frac{\partial K_{ℏ}}{\partial m} (m, r) | d m]}^{2} d r \\ + {\int_{s}^{t} {[\int_{r}^{t} [\int_{ℝ} | K (t - r, x - z) | \cdot | g (m, z) - g (r, z) | d z] | \frac{\partial K_{ℏ}}{\partial m} (m, r) | d m]}^{2} d r |}^{\frac{p}{2}} \end{matrix}$

$\begin{matrix} \leq 2^{p} {(C_{ℏ})}^{p} | \int_{s}^{t} {[\int_{r}^{t} {[\int_{ℝ} {| K (t - r, x - z) - K (t - m, x - z) |}^{q} | g (m, z) | d z]}^{\frac{1}{q}} {(m - r)}^{ℏ - \frac{3}{2}} d m]}^{2} d r {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{2} \\ + {\int_{s}^{t} {[\int_{r}^{t} {[\int_{ℝ} {| K (t - r, x - z) |}^{q} d z]}^{\frac{1}{q}} {[\int_{ℝ} {| g (m, z) - g (r, z) |}^{p} d z]}^{\frac{1}{p}} {(m - r)}^{ℏ - \frac{3}{2}} d m]}^{2} d r |}^{\frac{p}{2}} \\ \leq 2^{p} {(C_{ℏ})}^{p} | \int_{s}^{t} {[\int_{r}^{t} {(m - r)}^{γ_{1}} {(m - r)}^{ℏ - \frac{3}{2}} d m]}^{2} d r {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{2} \\ + {\int_{s}^{t} {[\int_{r}^{t} {(t - r)}^{\frac{q α - (p - 1)}{2 q α}} {(m - r)}^{γ_{2}} {(m - r)}^{ℏ - \frac{3}{2}} d m]}^{2} d r {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{2} |}^{\frac{p}{2}} \end{matrix}$

$\begin{matrix} = 2^{p} {(C_{ℏ})}^{p} {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} | \frac{1}{{(ℏ + γ_{1} - \frac{1}{2})}^{2} (2 ℏ + 2 γ_{1})} {(t - s)}^{2 ℏ + 2 γ_{1}} {+ \int_{s}^{t} \frac{1}{ℏ + γ_{2} - \frac{1}{2}} {(t - r)}^{\frac{q α - (p - 1)}{2 q α} + ℏ + γ_{2} - \frac{1}{2}} d r |}^{\frac{p}{2}} \\ \leq 2^{p} {(C_{ℏ})}^{p} {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} | \frac{1}{{(ℏ + γ_{1} - \frac{1}{2})}^{2} (2 ℏ + 2 γ_{1})} {(t - s)}^{2 ℏ + 2 γ_{1}} \\ + {\frac{1}{ℏ + γ_{2} - \frac{1}{2}} \frac{1}{\frac{q α - (p - 1)}{2 q α} + ℏ + γ_{2} + \frac{1}{2}} {(t - s)}^{\frac{q α - (p - 1)}{2 q α} + ℏ + γ_{2} + \frac{1}{2}} |}^{\frac{p}{2}} . \end{matrix}$

假设 $D (X, c) = D_{T} \cap Q_{c}$ 且 $Q_{c} = Q_{c} (t_{0}, x_{0})$ 。根据假设 $(t, x) \in Q_{c} (t_{0}, x_{0})$ ， $(s, y) \in Q_{c} (t_{0}, x_{0})$ ，有

$0 \leq t - s \leq 2 c^{2}, | x - y | \leq | x - x_{0} | + | y - y_{0} | \leq 2 c .$

由A-类有界区域的定义，有

${[u]}_{L^{p, θ} ((D_{T}; δ); L^{p} (Ω))}^{p} \leq C_{2} {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p},$

其中 $C_{2}$ 为一个常数， $θ = 1 + \frac{β p}{3}$ ，即不等式(7)成立。因此利用命题2.1可以得到不等式(8)。

下面证明不等式(9)。为了使用尾估计，我们首先考虑以下估计。设 $(t_{0}, x_{0}) \in D_{T} \subset O_{T}$ 且

$Q_{c} (t_{0}, x_{0}) = (t_{0} - c^{2}, t_{0} + c^{2}) \times B_{c} (x_{0}),$

则有 ${\bar{D}}_{T} \subset Q_{d (D)} (t_{0}, x_{0})$ 。设 $(t_{1}, x_{1}), (t_{2}, x_{2}) \in D_{T}$ ， $Q_{i} : = D_{T} \cap Q_{c_{i}} (t_{i}, x_{i}), i = 1, 2$ 并且

$F (t_{i}, x_{i}, c_{i}) = \frac{1}{{| Q_{i} |}^{1 + θ}} \int_{Q_{i}} \int_{Q_{i}} {| u (t, x) - u (s, y) |}^{p} d t d x d s d y = \frac{1}{{| Q_{i} |}^{1 + θ}} \int_{Q_{i}} \int_{Q_{i}} {| K g (t, x) - K g (s, y) |}^{p} d t d x d s d y .$

显然

$\begin{array}{l} F (t_{1}, x_{1}, c_{1}) - F (t_{2}, x_{2}, c_{2}) = [F (t_{1}, x_{1}, c_{1}) - F (t_{2}, x_{1}, c_{1})] \\ + [F (t_{2}, x_{1}, c_{1}) - F (t_{2}, x_{2}, c_{1})] \\ + [F (t_{2}, x_{2}, c_{1}) - F (t_{2}, x_{2}, c_{2})] \\ : = I_{1} + I_{2} + I_{3} . \end{array}$ (10)

对于 $I_{1}$ ，

$\begin{array}{l} I_{1} = F (t_{1}, x_{1}, c_{1}) - F (t_{2}, x_{1}, c_{1}) \\ = \frac{1}{{| Q_{1} |}^{1 + θ}} \int_{Q_{1}} \int_{Q_{1}} {| K g (t, x) - K g (s, y) |}^{p} d t d x d s d y \\ = \frac{1}{{| Q_{1} |}^{1 + θ}} \int_{Q_{1}} \int_{Q_{1}} {| K g (t, x) - K g (s, y) |}^{p} d t d x d s d y - \frac{1}{{| Q_{12} |}^{1 + θ}} \int_{Q_{12}} \int_{Q_{12}} {| K g (t, x) - K g (s, y) |}^{p} d t d x d s d y \\ = \frac{1}{{| Q_{1} |}^{1 + θ}} {\int_{Q_{1} \ Q_{12}} \int_{Q_{1} \ Q_{12}} {| K g (t, x) - K g (s, y) |}^{p} d t d x d s d y - \int_{Q_{12} \ Q_{1}} \int_{Q_{12} \ Q_{1}} | {| K g (t, x) - K g (s, y) |}^{p} d t d x d s d y} \\ + [\frac{1}{{| Q_{1} |}^{1 + θ}} - \frac{1}{{| Q_{12} |}^{1 + θ}}] \int_{Q_{12}} \int_{Q_{12}} {| K g (t, x) - K g (s, y) |}^{p} d t d x d s d y \\ : = I_{11} + I_{12}, \end{array}$

其中 $Q_{12} = D_{T} \cap Q_{c_{1}} (t_{2}, x_{1})$ 。为简单起见，我们假设 $| Q_{1} | \geq | Q_{12} |$ 。相反的，我们可以改变 $Q_{1}$ 和 $Q_{12}$ 的位置。因此 $I_{12} \leq 0$ 。现在考虑 $I_{11}$ 这一项。在给出 $I_{11}$ 的估计之前，我们首先回顾一下我们的目标。为了应用尾部估计，我们希望得到 $I_{11}$ 的估计，即存在 $δ > 0$ ，使得 $E I_{11} \leq C {(t_{1} - t_{2})}^{δ}$ 。显然

$| Q_{1} \ Q_{12} | \leq C (t_{1} - t_{2}) c_{1}, | Q_{1} | \approx C c_{1}^{3} .$

假设 $t > s$ ，则

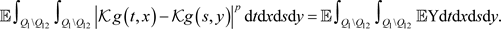
类似不等式(7)的证明有

$E Υ \leq C c_{1}^{β p} {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} .$

因为 $(t, x) \in Q_{1}$ ， $(s, y) \in Q_{1}$ ，所以 $0 \leq t - s \leq 2 c_{1}^{2}$ ， $| x - y | \leq | x - x_{1} | + | y - x_{1} | \leq 2 c_{1}$ ，利用上述不等式和A-类有界区域的性质有

$E \int_{Q_{1} \ Q_{12}} \int_{Q_{1} \ Q_{12}} E Υ d t d x d s d y \leq C (p, T) c_{1}^{β p} {| Q_{1} \ Q_{12} |}^{2} {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} .$

因为 $D_{T}$ 是一个A-类有界区域，所以 $2 c_{1} \leq | D |$ ，

$A | Q_{c_{1}} (t_{1}, x_{1}) | \leq | Q_{1} | \leq | Q_{c_{1}} (t_{1}, x_{1}) |,$

$A | Q_{c_{1}} (t_{1}, x_{1}) \ Q_{c_{1}} (t_{2}, x_{1}) | \leq | Q_{1} \ Q_{12} | \leq | Q_{c_{1}} (t_{1}, x_{1}) \ Q_{c_{1}} (t_{2}, x_{1}) | .$

注意到

$| Q_{c_{1}} (t_{1}, x_{1}) | \approx C c_{1}^{3}, | Q_{c_{1}} (t_{1}, x_{1}) \ Q_{c_{1}} (t_{2}, x_{1}) | \leq C c_{1} [c_{1}^{2} \land (t_{1} - t_{2})],$

其中C是一个不依赖于 $c_{1}$ 的正常数。显然 $Q_{1} \ Q_{12} \subset Q_{1}$ ，取 $0 < δ < \frac{β p}{2}$ 有

$E \int_{Q_{1} \ Q_{12}} \int_{Q_{1} \ Q_{12}} {| K g (t, x) - K g (s, y) |}^{p} d t d x d s d y \leq C (C_{0}, D, T) {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} {| Q_{1} |}^{2 + \frac{β p - 2 δ}{3}} {| t_{1} - t_{2} |}^{δ} .$

类似地，我们可以得到

$E \int_{Q_{12} \ Q_{1}} \int_{Q_{12 \ Q_{1}}} {| u (t, x) - u (s, y) |}^{p} d t d x d s d y \leq C (D, T) {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} {| Q_{1} |}^{2 + \frac{β p - 2 δ}{3}} {| t_{1} - t_{2} |}^{δ} .$

由 $I_{12} \leq 0$ 有

$E I_{1} \leq C (D, T) {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} {| t_{1} - t_{2} |}^{δ},$ (11)

其中 $θ = 1 + \frac{β p - 2 δ}{3}$ 。

接下来我们估计 $I_{2}$ 。利用事实

$| [D \cap Q_{c_{1}} (t_{2}, x_{1})] \ [D \cap Q_{c_{1}} (t_{2}, x_{2})] | \leq C c_{1}^{2} | x_{1} - x_{2} |,$

类似于 $I_{1}$ 的估计，可以取 $0 < δ < \frac{β p}{2}$ 使得

$E I_{2} = E [F (t_{2}, x_{1}, c_{1}) - F (t_{2}, x_{2}, c_{1})] \leq C (D, T) {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} {| x_{1} - x_{2} |}^{δ},$ (12)

其中 $θ = 1 + \frac{β p - δ}{3}$ 。

下面估计 $I_{3}$ 。利用事实

$| [D \cap Q_{c_{1}} (t_{2}, x_{2})] \ [D \cap Q_{c_{2}} (t_{2}, x_{2})] | \leq C c_{1}^{2} (c_{1} - c_{2}), c_{1} \geq c_{2},$

类似于 $I_{1}$ 的估计有

$E I_{3} = E [F (t_{2}, x_{2}, c_{1}) - F (t_{2}, x_{2}, c_{2})] \leq C (D, T) {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p} {| c_{1} - c_{2} |}^{δ},$ (13)

其中 $θ = 1 + \frac{β p - δ}{3}$ 。因此根据公式(10)，(11)，(12)和(13)，有

$E {| F (t_{1}, x_{1}, c_{1}) - F (t_{2}, x_{2}, c_{2}) |}^{q} \leq C (D, T) {‖ g ‖}_{D^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p q} {(| t_{1} - t_{2} | + | x_{1} - x_{2} | + | c_{1} - c_{2} |)}^{δ q},$

其中 $θ = 1 + \frac{β p - 2 δ}{3}, (t_{i}, x_{i}) \in D_{T}$ 且 $0 < c_{i} \leq | D |, i = 1, 2$ 。

设 $D_{T} = {[0, 1]}^{2}$ ， $c \in [0, 2]$ 。引入一系列集合，

$S_{n} = {z \in ℤ^{3} ∣ z 2^{- n} \in {(0, 1)}^{2} \times (0, 2)}, n \in ℕ .$

对于任意的 $e = (e_{1}, e_{2}, e_{3}) \in ℤ^{3}$ 使得 ${| e |}_{\infty} = \max_{1 < i < 3} | e_{j} | = 1$ ，并且对于任意的 $z, z + e \in S_{n}$ ，定义 $v_{z}^{n, e} = | F ((z + e) 2^{- n}) - F (z 2^{- n}) |$ 。从上面的讨论，可以得到

$E {| v_{z}^{n, e} |}^{q} \leq C (β, C_{0}, D, T) {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p q} 2^{- n δ q} : = \hat{C} 2^{- n δ q} .$

对于任意的 $τ > 0$ ， $K > 0$ ，

$A_{z, τ}^{n, e} = {ω \in Ω | v_{z}^{n, e} \geq K τ^{n}, z, z + e \in S_{n}},$

从而

$ℙ (A_{z, τ}^{n, e}) \leq \frac{E {| v_{z}^{n, e} |}^{q}}{K^{q} τ^{q n}} \leq \frac{\hat{C} 2^{- n q}}{K^{q} τ^{q n}} .$

对于每一个n，事件的总数 $A_{z, τ}^{n, e}, z, z + e \in S_{n}$ 不大于 $2^{3} 3^{3}$ 。因此并集为

$A_{τ}^{n} = \cup_{z, z + e \in S_{n}} (\cup_{{‖ e ‖}_{\infty} = 1} A_{z, τ}^{n, e}),$

并集的概率为

$ℙ (A_{τ}^{n}) \leq \frac{\hat{C} 2^{- n δ q}}{K^{q} τ^{q n}} 2^{3 n} \leq \hat{C} K^{- q} {(\frac{2^{3}}{{(2^{δ} τ)}^{q}})}^{n} .$

设 $τ = 2^{- v δ}$ ，其中 $v > 0$ 且 $(1 - v) δ q \geq 3$ 。事件 $A = \cup_{n \geq 1} A_{τ}^{n}$ 发生的概率为

$ℙ (A) \leq C \hat{C} K^{- q} .$ (14)

对于任意一点 $ξ = (t, x, c) \in {(0, 1)}^{2} \times (0, 2)$ 有 $ξ = \sum_{i = 0}^{\infty} e_{i} 2^{- i} ({‖ e_{i} ‖}_{\infty} \leq 1)$ ， $ξ_{k} = \sum_{i = 0}^{k} e_{i} 2^{- i}$ 且 $ξ_{0} = 0$ 。对于任意的 $ω \notin A$ ， $| F (ξ_{k + 1}) - F (ξ_{k}) | < K τ^{k + 1}$ ，这意味着

$| F (t, x, c) | \leq \sum_{k = 0}^{\infty} | F (ξ_{k + 1}) - F (ξ_{k}) | < K \sum_{k = 1}^{\infty} τ^{k} \leq K {(2^{ν δ} - 1)}^{- 1} .$ (15)

设 $v_{1} = \sup_{(t, x, c) \in {(0, 1)}^{2} \times (0, 2)} | F (t, x, c) |$ ，由于F是连续的，则 $v_{1} = \sup_{(t, x, c) \in {(0, 1)}^{2} \times (0, 2)} | F (t, x, c) |$ 。对于 $0 < r < q$ ，

$E v_{1}^{r} = r \int_{0}^{\infty} a^{r - 1} ℙ (v_{1} \geq a) d a = r \int_{0}^{γ K} a^{r - 1} ℙ (v_{1} \geq a) d a + r \int_{γ K}^{\infty} a^{r - 1} ℙ (v_{1} \geq a) d a .$ (16)

选择 $γ \geq {(2^{v δ} - 1)}^{- 1}$ ，利用(14)，(15)和(16)有

$E v_{1}^{r} \leq {(γ K)}^{r} + C {\hat{C}}^{q} r \int_{γ K}^{\infty} a^{r - 1 - q} d a \leq {(γ K)}^{r} + C \hat{C} r {(c K)}^{r - q},$

从而

$E v_{1}^{r} \leq C (D, d, T) {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ^{d})))}^{p r},$

如果选择 $K = {‖ g ‖}_{L^{p} (Ω; L^{\infty} ([0, T]; L^{p} (ℝ)))}^{p}$ 。通过使用嵌入不等式 $L^{p} (Ω; L^{p, θ} (D_{T}; δ)) ≅ L^{p} (Ω; C^{γ} ({\bar{D}}_{T}; δ))$ ，得到不等式。

4. 总结

本文利获得了非局部随机扩散方程解的Hölder连续性。首先利用Campanato估计证明了非局部随机扩散方程的温和解的Hölder连续性，即解u属于空间 $C^{β} (D_{T}; L^{p} (Ω))$ ，其中 $β$ 为确定的Hölder连续指数。其次，通过使用尾估计和Sobolev嵌入定理得到了 $L^{p} (Ω; C^{β^{*}} (D_{T}))$ 中温和解的估计。更重要的是，我们在 $β$ 和 $β^{*}$ 两个指数之间给出了一个明确的公式。

基金项目

天津师范大学研究生科研创新项目资助(2022KYCX114Y)。

文章引用

贾倩,王伟. 非局部随机扩散方程解的H?lder连续性
H?lder Continuous of the Solutions to Nonlocal Stochastic Diffusion Equations[J]. 理论数学, 2023, 13(12): 3380-3394. https://doi.org/10.12677/PM.2023.1312351

参考文献

1. Kim, I. (2015) A BMO Estimate for Stochastic Singular Integral Operators and Its Application to SPDEs. Journal of Functional Analysis, 269, 1289-1309. https://doi.org/10.1016/j.jfa.2015.05.015

2. Lv, G., Gao, H., Wei, J. and Wu, J.L. (2019) BMO and Morrey-Campanato Estimates for Stochastic Convolutions and Schauder Estimates for Sto-chastic Parabolic Equations. Differential Equations, 266, 2666-2717. https://doi.org/10.1016/j.jde.2018.08.042

3. Krylov, N.V. (1999) An Analytic Approach to SPDEs. In: Sto-chastic Partial Differential Equations: Six Perspectives, Vol. 64, AMS, Providence, 185-242. https://doi.org/10.1090/surv/064/05

4. Krylov, N.V. (1996) On Lp-Theory of Stochastic Partial Differential Equations in the Whole Space. SIAM Journal on Mathematical Analysis, 27, 313-340. https://doi.org/10.1137/S0036141094263317

5. Kim, I. and Kim, K.H. (2016) An Lp-Theory for Stochastic Partial Differential Equations Driven by Lévy Processes with Pseudo-Differential Operators of Arbitrary Order. Sto-chastic Processes and their Applications, 126, 2761-2786. https://doi.org/10.1016/j.spa.2016.03.001

6. Zhang, X. (2006) Lp-Theory of Semi-Linear SPDEs on General Measure Spaces and Applications. Journal of Functional Analysis, 239, 44-75. https://doi.org/10.1016/j.jfa.2006.01.014

7. Zhang, X. (2013) Lp-Maximal Regularity of Nonlocal Parabolic Equations and Applications. Annales de l’Institut Henri Poincaré C, 30, 573-614. https://doi.org/10.1016/j.anihpc.2012.10.006

8. Duncan, T.E., Pasik-Duncan, B. and Maslowski, B. (2002) Fractional Brownian Motion and Stochastic Equations in Hilbert Spaces. Stochastics and Dynamics, 2, 225-250. https://doi.org/10.1142/S0219493702000340

9. Comte, F. and Renault, E. (1996) Long Memory Continuous Time Models. Journal of Econometrics, 73, 101-149. https://doi.org/10.1016/0304-4076(95)01735-6

10. Boufoussi, B. and Hajji, S. (2012) Neutral Stochastic Func-tional Differential Equations Driven by a Fractional Brownian Motion in a Hilbert Space. Statistics and Probability Letters, 82, 1549-1558. https://doi.org/10.1016/j.spl.2012.04.013

11. Caraballo, T., Garrido-Atienza, M.J. and Taniguchi, T. (2011) The Existence and Exponential Behavior of Solutions to Stochastic Delay Evolution Equations with a Fractional Brownian Motion. Nonlinear Analysis: Theory, Methods and Applications, 74, 3671-3684. https://doi.org/10.1016/j.na.2011.02.047

12. Li, Z. and Yan, L. (2019) Ergodicity and Stationary Solution for Stochastic Neutral Retarded Partial Differential Equations Driven by Fractional Brownian Motion. Journal of Theoretical Probability, 32, 1399-1419. https://doi.org/10.1007/s10959-018-0810-8

13. Xu, L., Li, Z. and Luo, J. (2017) Global Attracting Set and Ex-ponential Decay of Second-Order Neutral Stochastic Functional Differential Equations Driven by fBm. Advances in Difference Equations, 2017, Article No. 134. https://doi.org/10.1186/s13662-017-1186-2

14. Hsu, E.P., Wang, Y. and Wang, Z. (2017) Stochastic De Giorgi Iteration and Regularity of Stochastic Partial Differential Equations. The Annals of Probability, 45, 2855-2866. https://doi.org/10.1214/16-AOP1126

15. Du, K. and Liu, J. (2016) A Schauder Estimate for Stochastic PDEs. Comptes Rendus Mathematique, 354, 371-375. https://doi.org/10.1016/j.crma.2016.01.010

16. Debussche, A., De Moor, S. and Hofmanová, M. (2015) A Reg-ularity Result for Quasilinear Stochastic Partial Differential Equations of Parabolic Type. SIAM Journal on Mathematical Analysis, 47, 1590-1614. https://doi.org/10.1137/130950549

17. Kuksin, S.B., Nadirashvili, N.S. and Piatnitski, A.L. (2003) Hölder Esti-mates for Solutions of Parabolic SPDEs. Theory of Probability and Its Applications, 47, 157-163. https://doi.org/10.1137/S0040585X97979524

18. Tian, R., Ding, L., Wei, J. and Zheng, S. (2019) Hölder Esti-mates of Mild Solutions for Nonlocal SPDEs. Advances in Difference Equations, 2019, Article No. 159. https://doi.org/10.1186/s13662-019-2097-1

19. Lv, G., Gao, H., Wei, J. and Wu, J.L. (2023) On the Campanato and Hölder Regularity of Local and Nonlocal Stochastic Diffusion Equations. Discrete and Continuous Dynamical Systems-B, 28, 1244. https://doi.org/10.3934/dcdsb.2022119

20. Chen, Y.Z. (2003) Second Order Parabolic Partial Differential Equa-tions. Peking University Press, Beijing.

21. Bogdan, K. and Jakubowski, T. (2007) Estimates of Heat Kernel of Frac-tional Laplacian Perturbed by Gradient Operators. Communications in Mathematical Physics, 271, 179-198. https://doi.org/10.1007/s00220-006-0178-y

22. Bogdan, K., Stós, A. and Sztonyk, P. (2003) Harnack Inequality for Stable Processes on d-Sets. Studia Mathematica, 158, 163-198. https://doi.org/10.4064/sm158-2-5

23. Chen, Z.Q. and Hu, E. (2015) Heat Kernel Estimates for Δ+Δα/2 under Gradient Perturbation. Stochastic Processes and Their Applications, 125, 2603-2642. https://doi.org/10.1016/j.spa.2015.02.016

24. Imbert, C. (2005) A Non-Local Regularization of First Order Hamilton-Jacobi Equations. Journal of Differential Equations, 211, 218-246. https://doi.org/10.1016/j.jde.2004.06.001

25. Biagini, F., Hu, Y., Φksendal, B. and Zhang, T. (2008) Stochastic Calculus for Fractional Brownian Motion and Applications. Springer Science and Business Media, Berlin. https://doi.org/10.1007/978-1-84628-797-8

NOTES

^*通讯作者。

期刊菜单