Applied Physics
Vol.05 No.11(2015), Article ID:16422,7
pages
10.12677/APP.2015.511020
Stochastic Resonance in a Tumor Cell Growth System Driven by a Colored Noise and Periodic Excitation
Hang Li, Ziming Liu, Shenghong Li*
School of Mathematics and Physics, Jiangsu University of Science and Technology, Zhenjiang Jiangsu
Received: Nov. 7th, 2015; accepted: Nov. 24th, 2015; published: Nov. 27th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, stochastic resonance in a tumor cell growth system driven by a colored noise and periodic excitation is investigated. According to Novikov theorem and unified colored noise theory, the related Fokker-Plank equation and the stable probability density function are obtained. Based on theory, we present the explicit expression of signal-to-noise ratio. Conclusions are that: stochastic resonance produced as noise strength is little and its strength is increased as tumor cell growth rate and amplitude of periodic effect are increased respectively. But the carrying capacity has no obvious impact on the strength of stochastic resonance, however, the more carrying capacity is, the more the required noise strength to attain stochastic resonance is.
Keywords:Tumor Cell Growth System, Colored Noise, Stochastic Resonance, Signal-to-Noise Rate

色噪声和周期激励下肿瘤细胞 增长系统的随机共振
李行,刘子铭,李胜宏*
江苏科技大学数理学院,江苏 镇江

收稿日期:2015年11月7日;录用日期:2015年11月24日;发布日期:2015年11月27日

摘 要
本文研究了色噪声驱动下肿瘤细胞增长系统的随机共振现象,根据Novikov定理和统一色噪声理论,得到了相应的FPK方程,并给出了稳态概率密度函数的表达式。运用绝热近似理论,得到了信噪比的解析表达式。结果表明,在噪声强度较小时产生了随机共振,且其强度随着增长率和周期作用振幅的增大而增强,而承载能力对随机共振强度没有显著影响,但承载能力越大,要达到共振所需要的噪声强度也越大。
关键词 :肿瘤细胞增长系统,色噪声,随机共振,信噪比

1. 引言
随机共振的概念是由Benzi等[1] 和Nicolis等[2] 在研究第四纪全球气象冰川问题时提出的。不同于通常人们对噪声的直观认识,由于随机共振现象体现了噪声的积极作用,因而引起了人们极大的兴趣。1983年,Fauve [3] 第一次在Schmitt触发器电路系统的实验中发现了随机共振现象的存在,并把信噪比的概念引入到随机共振的研究。后来,McNamera和Wiesenfeld等[4] 发展了绝热近似理论,得到了信噪比的解析表达式。此后随机共振在很多学科领域中得到了广泛的研究和初步应用,领域涵盖了物理、通信、光学、生物、神经网络等,并获得了丰硕的成果。
逻辑增长模型是细菌细胞增长和肿瘤细胞增长的一个基本模型,[5] [6] 研究了色噪声驱动下细菌增长系统的随机共振现象,结果表明噪声能够引起随机共振,在细菌的控制和治疗中具有一定的实际意义。本文研究了色噪声驱动下肿瘤细胞增长系统的随机共振现象,运用绝热近似理论和统一色噪声近似理论,获得了信噪比的表达式,并用数值模拟曲线分析了各参数对随机共振的影响,据此可以控制系统参数和噪声参数,使周期激励的治疗效果更好。
2. 肿瘤细胞增长系统的信噪比
肿瘤细胞增长模型为[7]
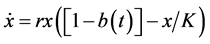 (1)
(1)
其中x是肿瘤细胞群,r是增长率,K是承载能力,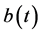 是周期函数,表示对肿瘤细胞群的周期激励作用. (图1)如果
是周期函数,表示对肿瘤细胞群的周期激励作用. (图1)如果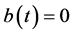 ,表示没有激励,平衡点是K;如果
,表示没有激励,平衡点是K;如果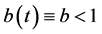 ,那么平衡点是
,那么平衡点是 。相反,若
。相反,若 ,则平衡点为0。如果对所有的t,
,则平衡点为0。如果对所有的t, 是正数,那么肿瘤细胞的增长率减小,且平衡点在0和K之间;反之,若
是正数,那么肿瘤细胞的增长率减小,且平衡点在0和K之间;反之,若 对某一t是负数,则肿瘤细胞群有一个负的增长率,肿瘤细胞被杀死,最终有一个零平衡。这里我们选择
对某一t是负数,则肿瘤细胞群有一个负的增长率,肿瘤细胞被杀死,最终有一个零平衡。这里我们选择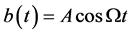 ,A为振幅,
,A为振幅,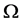 是周期作用的频率,再考虑环境的影响
是周期作用的频率,再考虑环境的影响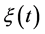 (包括温度、PH值和离子强度等),这样方程(1)改写为
(包括温度、PH值和离子强度等),这样方程(1)改写为
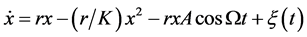 (2)
(2)
这里 是指数型的高斯色噪声,具有如下统计性质
是指数型的高斯色噪声,具有如下统计性质
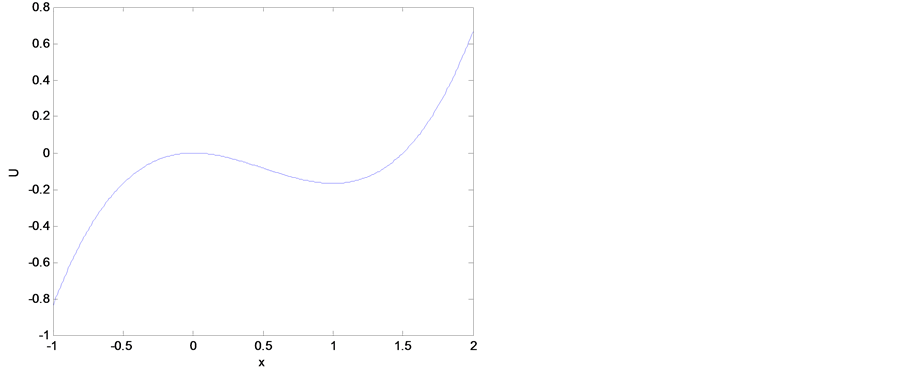
Figure 1. Potential function of the tumor cell growth system as r = K = 1
图1. 当r = K = 1时,肿瘤细胞增长系统的势函数
 (3)
(3)
其中D是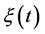 的强度,
的强度,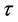 是其相关时间。方程(2)的势函数为
是其相关时间。方程(2)的势函数为
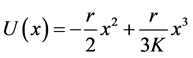 (4)
(4)
当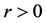 时,有一个不稳定点
时,有一个不稳定点 和一个稳定点
和一个稳定点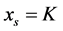 。反之,当
。反之,当 时,有一个稳定点
时,有一个稳定点 和一个不稳定点
和一个不稳定点 。
。
根据Novikov定理[8] 和统一色噪声近似理论[9] ,方程(2)相应的FPK方程为
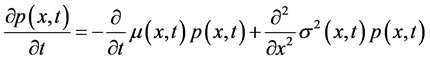 (5)
(5)
其中
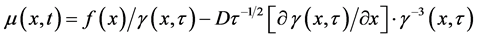


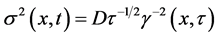 (6)
(6)
由式(5)和式(6),可解得其稳态概率密度函数为
 (7)
(7)
这里C为归一化常数,
 (8)
(8)
这里我们仅就 的情况讨论,
的情况讨论, 时的情况与此类似。利用平均首通时间的定义和文献,从稳定状态
时的情况与此类似。利用平均首通时间的定义和文献,从稳定状态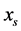 出发到达不稳定状态
出发到达不稳定状态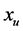 的平均首通时间表达式为
的平均首通时间表达式为
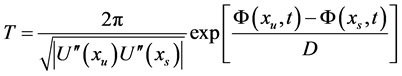 (9)
(9)
上式成立要求 ,即势垒高度远远大于噪声的强度D。从而得到克莱斯勒逃逸速率
,即势垒高度远远大于噪声的强度D。从而得到克莱斯勒逃逸速率
 (10)
(10)
根据McNamara和Wiesenfeld提出的绝热近似条件下的信噪比理论,得到方程(2)的输出总信号功率和信噪比表达式为
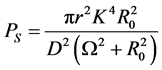 (11)
(11)
 (12)
(12)
其中 。
。
当A»1时,式(11)的括号中第二项可略去,则有
 (13)
(13)
这就是方程(2)在绝热近似条件下的输出信噪比表达式。
3. 数值结果
为考察随机共振产生与否,我们借助于数值图像来讨论噪声强度对输出总信号功率的影响。图2给出了输出总信号功率P随噪声强度D变化的函数关系,在小D时,增加噪声强度十分有效地提高了输出总信号功率,即产生了共振,说明在一定范围内,适当的增加噪声强度有助于提高周期激励的治疗效果。
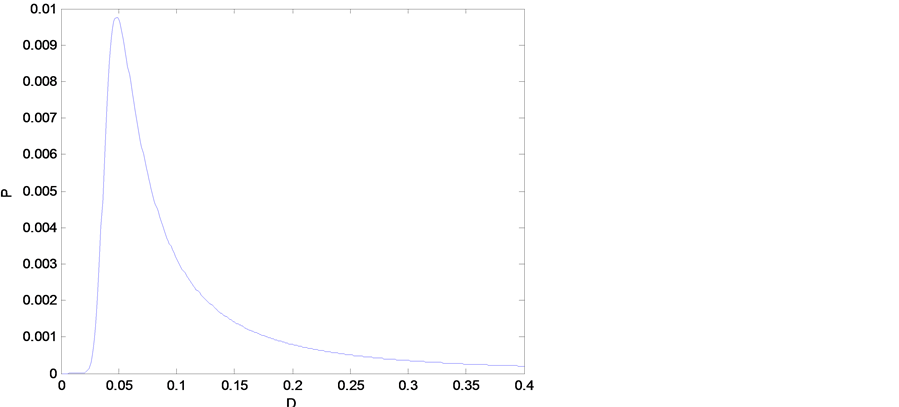
Figure 2. The relationship between total power of output signal and noise intensity (r = K = 1, A = Ω = 0.01)
图2. 输出信号总功率与噪声强度的关系(r = K = 1, A = Ω = 0.01)
式(13)给出了信噪比的解析表达式,下面在满足绝热近似的条件下,讨论不同参数对信噪比的影响。
图3描述了不同增长率下,信噪比随噪声强度变化的函数关系。从图中可以看到,随着噪声强度的变化,信噪比曲线出现了单峰,产生了随机共振。共振峰随着增长率r的增加而增大,说明r越大,随机共振强度越大。同时共振峰随着r的增加而向右移动,说明增长率越大,要达到随机共振所需要的噪声强度也在增加,这与实际是符合的。因此通过调节噪声强度D可以控制随机共振。
图4显示了信噪比作为噪声强度的函数随承载能力K变化的曲线。同样,随着噪声强度的增加,信噪比曲线出现了单峰,产生随机共振。随着承载能力K的增强,共振峰向右移动,表明承载能力越强,
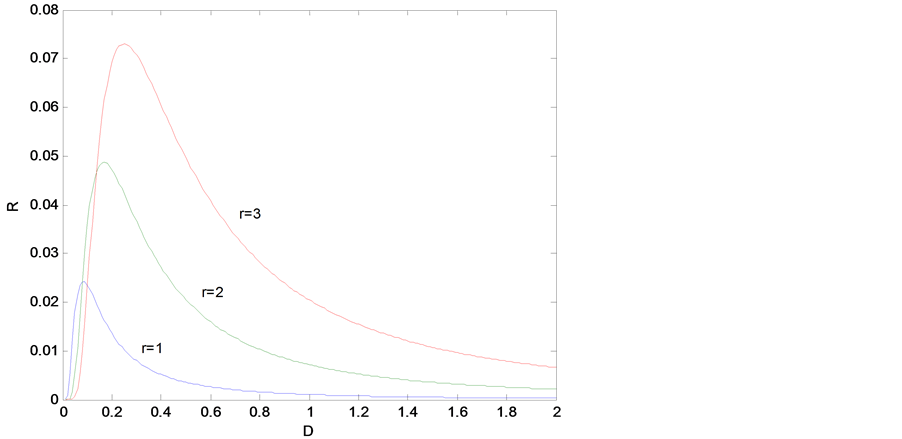
Figure 3. Vary of signal-to-noise ratio as a function of noise intensity with growth ratio r (A = 0.1, K = 1)
图3. 信噪比作为噪声强度的函数随增长率的变化(A = 0.1, K = 1)
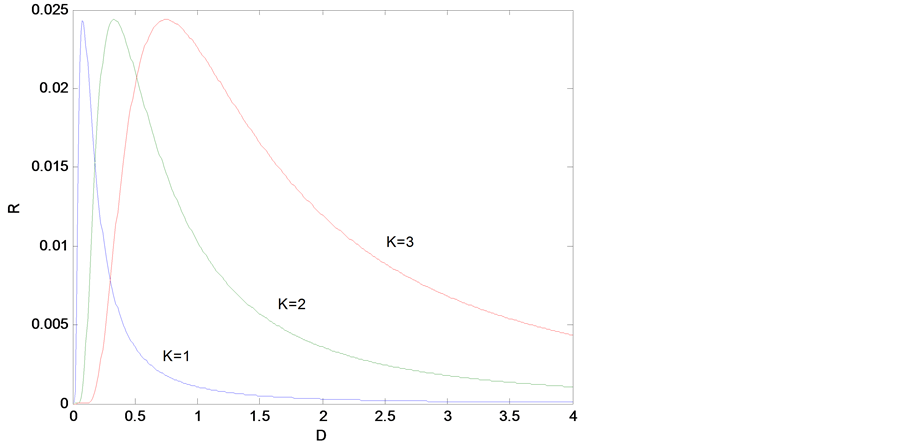
Figure 4. Vary of signal-to-noise ratio as a function of noise intensity with carrying capacity K (r = 1, A = 1)
图4. 信噪比作为噪声强度的函数随承载能力的变化曲线(r = 1, A = 1)
要达到随机共振所需要的噪声强度也越强。但是承载能力K对峰值没有显著影响,即对随机共振的强度没有显著影响。
图5描述了信噪比作为噪声强度的函数随着激励振幅的变化的情况,表明激励强度越大,发生随机共振的强度也越大,但这种共振受噪声强度的影响不显著,都是在 时达到了共振。同时从图6看
时达到了共振。同时从图6看

Figure 5. Vary of signal-to-noise ratio as a function of noise intensity with periodic excitation amplitude A (r = K = 1)
图5. 信噪比作为噪声强度的函数随振幅的变化曲线(r = K = 1)

Figure 6. Vary of signal-to-noise ratio as a function of noise intensity with periodic excitation frequency (r = K = 1, A = 0.01)
图6. 信噪比作为噪声强度的函数随频率的变化曲线(r = K = 1, A = 0.01)
到,信噪比作为噪声强度的函数随频率变化的三条曲线几乎是重合的,说明随机共振几乎不受激励频率的影响。
4. 结论
本文研究了色噪声和周期治疗驱动下肿瘤细胞增长系统的随机共振。结果表明,在噪声强度较小时产生了随机共振,并且随机共振也受到系统中各参数的影响。随机共振的强度随着增长率和周期激励振幅的增加而增加,而承载能力和周期激励的频率对随机共振的强度没有显著影响。因此我们可以通过调节噪声强度、增长率和周期激励振幅来控制随机共振,以达到更好的治疗效果。
文章引用
李行,刘子铭,李胜宏. 色噪声和周期激励下肿瘤细胞增长系统的随机共振
Stochastic Resonance in a Tumor Cell Growth System Driven by a Colored Noise and Periodic Excitation[J]. 应用物理, 2015, 05(11): 147-153. http://dx.doi.org/10.12677/APP.2015.511020
参考文献 (References)
- 1. Benzi, R., Sutera, A. and Vulpiani, A. (1981) Stochastic Resonance in Climatic Change. Journal of Physics A: Mathematical and Theoretical, 14, L453-L457. http://dx.doi.org/10.1088/0305-4470/14/11/006
- 2. Nicolis, C. and Nicolis, G. (1981) Stochastic Aspect of Climatic Transitions Additive Fluctuations. Tellus, 33, 225-234. http://dx.doi.org/10.1111/j.2153-3490.1981.tb01746.x
- 3. Fauve, S. and Helslot, F. (1983) Stochastic Resonance in a Bistable System. Physics Letters A, 97, 5-7. http://dx.doi.org/10.1016/0375-9601(83)90086-5
- 4. McNamara, B. and Wiesenfeld, K. (1989) Theory of Stochastic Resonance. Physics Review A, 39, 4854-4869. http://dx.doi.org/10.1103/PhysRevA.39.4854
- 5. Liao, H.Y., Ai, B.Q. and Hu, L. (2008) A New Logistic Model for Bacterial Growth in the Presence of a Gaussian Colored Moise. Brazilian Journal of Physical, 37, 1125. http://dx.doi.org/10.1590/S0103-97332007000700009
- 6. Zeng, C.H., Zhou, X.F., et al. (2009) Stochastic Resonance in a Bacterium Growth System Subjected to Colored Noises. Communications in Theoretical Physics, 52, 615-618. http://dx.doi.org/10.1088/0253-6102/52/4/12
- 7. Panetta, J.C. (1995) A Logistic Model of Periodic Excitation. Applied Mathematics Letters, 8, 83-86. http://dx.doi.org/10.1016/0893-9659(95)00053-S
- 8. Novikov, E.A. (1965) Functional and Random-Force Method in Turbulence Theory. Soviet Physics—JETP, 20, 1290.
- 9. Jung, P. and Haanggi, P. (1987) Dynamical Systems: A Unified Colored-Noise Approximation. Physical Review A, 35, 4464-4466. http://dx.doi.org/10.1103/PhysRevA.35.4464