Applied Physics
Vol.07 No.04(2017), Article ID:20276,6
pages
10.12677/APP.2017.74014
Comparison of Collision Dynamics of Non-Spherical Particles between the Hard-Particle Model and Soft-Particle Model
Daling Wu1, Nan Gui 2
1Zhejiang Academy of Safety Science and Technology, Hangzhou Zhejiang
2Institute of Nuclear and New Energy Technology, Tsinghua University, Key Laboratory of Advanced Reactor Engineering and Safety, Ministry of Education, Beijing

Received: Apr. 6th, 2017; accepted: Apr. 20th, 2017; published: Apr. 27th, 2017

ABSTRACT
Non-spherical particles and complex non-spherical particle systems are commonly encountered in energy chemical engineering, mineral engineering, and safety manufacturing engineering. The collision dynamics of non-spherical particles are fundamental issues in the investigations of complex particle systems. Discrete element method is the most prevalent models for particle-particle collision of spherical shapes, which incorporates a spring, a dashpot, and a frictional interaction. In this work, a comparative and analytical study on the mathematical models of collision dynamics for non-spherical particles is carried out. The hard non-spherical particle model and the soft-par- ticle model have been compared. It indicates that agreeable simulation results can be found for the two models. The two models have different advantages or disadvantages in accuracy, computational stability, and feasibility, with particular suitability for different cases.
Keywords:Energy Engineering, Chemical Engineering, Safety Manufacturing, Non-Spherical, Collision Model, Discrete Element Method, Hard Particle, Soft-Particle
非球形颗粒碰撞过程硬颗粒与软颗粒模型比较研究
吴达岭1,桂南2
1浙江省安全生产科学研究院,浙江 杭州
2清华大学核能与新能源技术研究院,先进反应堆工程与安全教育部重点实验室,北京
收稿日期:2017年4月6日;录用日期:2017年4月20日;发布日期:2017年4月27日

摘 要
在能源化工过程、矿业冶金及安全生产过程中均会涉及复杂的实际非球形颗粒体系,而颗粒的非球形碰撞动力学过程是对复杂颗粒体系进行研究必须要考虑的基本问题。离散元方法通过弹簧、阻尼、摩擦三种力学特性对颗粒-颗粒接触力进行建模,是目前国际上最为广泛使用的针对球形颗粒体系的模型。本文对典型三角形非球形碰撞动力学工程过程进行理论分析和模型比较研究,对国际上目前正在研究的硬颗粒和软颗粒非球形碰撞模型进行了比较。通过模型比较,证明了在工程上可以接受的计算误差范围内,软颗粒和硬颗粒计算结果吻合较好,两者在计算精度、稳定性、适用性方面各有优势,可以在不同的应用场合分别采用不同的计算模型。
关键词 :能源工程,化工过程,安全生产,非球形,碰撞模型,离散元,硬颗粒,软颗粒

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在能源工程、化工工程、矿冶工程、安全生产等过程中均会涉及不同的颗粒流动过程,比如颗粒流化过程、粉碎过程、包覆过程、传热过程等。对工业过程复杂颗粒体系行为的研究是颗粒学研究的一项中心课题。其目的是为了了解微观颗粒动力学特性与颗粒体系的宏观行为之间的相互关系 [1] 。
在理论研究中,离散元方法由于能提供几乎全部的碰撞动力学信息,包括每个颗粒的轨迹,瞬时相互作用力等,因而在过去的十几年中获得了越来越广泛的应用。离散元方法属于确定性模型,分为软球模型和硬球模型两种实现途径。硬球模型 [2] [3] 完全忽略颗粒形变,通过颗粒之间的相对位置和动量和角动量守恒来求解碰撞动力学过程,其中非完全弹性碰撞特性和摩擦则通过恢复系数和摩擦系数引入,多用于求解二体碰撞动力学。软球模型 [4] [5] 通过计算颗粒受力、形变及形变历史求解碰撞过程,可同时处理多体碰撞动力学。
最近,作者提出了针对非球形颗粒碰撞过程的硬颗粒模型(GHPM) [6] 和软颗粒模型(SIPHPM) [7] 。其中硬颗粒模型GHPM拓展了原硬球模型的思想,给出了任意形状非球形理想硬质颗粒碰撞动力学过程的解析解;软颗粒模型(SIPHPM)则提出基于在任意非球形形状的颗粒边界线上依次嵌入软质小球颗粒,通过模拟小颗粒之间,及小颗粒包围的面与其他非球形颗粒的小颗粒之间的碰撞过程,建立非球形颗粒之间的接触力学模型的思路。
虽然两者均通过理论解及实验过程给出了相应的验证。但两者之间并无比较何种解法更有优势。在此,将通过模拟相同情形下三角形颗粒的碰撞过程给出两个模型的模拟结果的比较。
2. 数值模型及工况
据牛顿第二定律,碰撞过程中颗粒运动遵守动量和角动量守恒关系。由于篇幅限制,对硬颗粒GHPM模型和软颗粒SIPHPM模型的详细推导过程及碰撞后颗粒运动的解可见参考文献 [6] 和 [7] 。这里不再赘述。
为了便于比较和进行能量分析,需要引入非球形颗粒碰撞过程的平动动能、转动动能和总动能的表达式,分别如下:
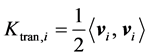 (1)
(1)
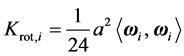 (2)
(2)
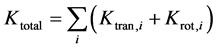 (3)
(3)
其中,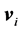 ,
,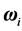 ,a分别表示颗粒的速度、角速度矢量和边长,i表示颗粒索引。由于质量为常量,在此处可不计。
,a分别表示颗粒的速度、角速度矢量和边长,i表示颗粒索引。由于质量为常量,在此处可不计。
本文采用的计算参数如表1所示。模拟的工况参数如表2所示,分别模拟了对心正碰和偏心碰过程的碰撞动力学过程。
3. 模拟结果对比
3.1. 工况1 (对心碰)
如图1(a)所示,其中绿色散点标记为SIPHPM软颗粒碰撞前后位置,蓝色实线标记为GHPM硬颗粒碰撞前后位置,两者重合处为深色。速度矢量用红色标记。从图1(a)可见,SIPHPM和GHPM的模拟结果无论碰撞前后都相差无几。从矢量关系可见,碰撞前后两颗粒碰撞东南发生交换。
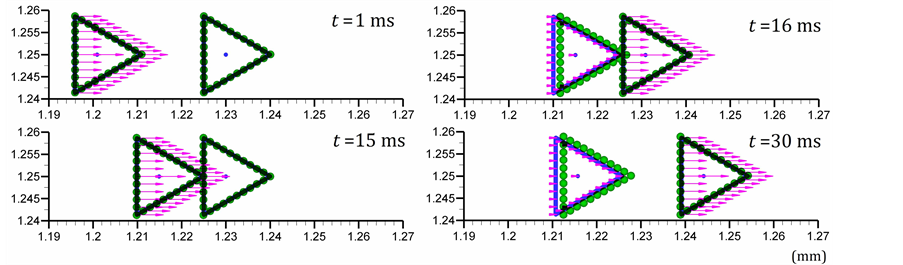
图1(b)的定量分析结果给出:
1) 硬颗粒模拟结果(图1(b)左),颗粒1 (西侧颗粒,下同)平动动能由0.5降到0,颗粒2 (东侧颗粒,下同)平动动能由0增加到约0.45左右,两者的总动能由0.5下降到0.45 (恢复系数0.5,见表1)。表明碰撞过程中颗粒1和颗粒2发生了动量交换,颗粒1将大部分(90%)的动能传递给颗粒2。碰撞过程中发生了10%的动能损失,这是由于恢复系数为0.9导致的;
2) 软颗粒模拟结果(图1(b)右),颗粒1和颗粒2在碰撞前后的动能变化与硬颗粒的模拟结果是相似的。不同之处在于,碰撞形变过程中,颗粒系统的动能向形变弹性势能转换,总动能降低,至形变最大处发生转折,其后形变逐渐恢复,弹性势能向颗粒动能转化,使得总动能增加,并恢复至0.45 (受恢复系数0.9即非完全弹性形变限制所致)。由于动能和形变弹性势能的相互转换过程持续时间极短(如图1(b)所示,持续不超过0.005 s),且迅速恢复到碰撞后的速度,故此转换过程对颗粒宏观速度的影响可以忽略。
由此可见,硬颗粒和软颗粒模型均能用于模拟非球形颗粒对心碰过程,两者吻合很好。而软颗粒模型由于采用弹簧力学模型,很好地体现并解释了她与硬颗粒模型在求解碰撞微观过程中的不同。
3.2. 工况2 (偏心碰)
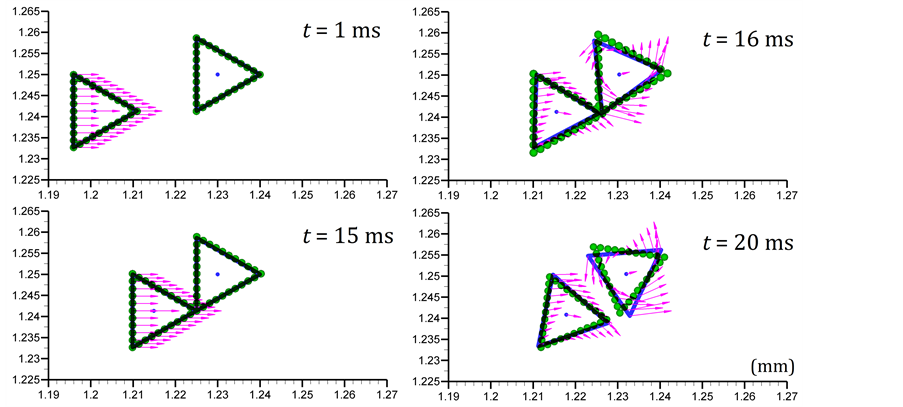
如图2则显示了偏心碰撞过程,偏心距离为a/2。从图2(a)可见,虽然颗粒1和2的初始速度仍和工况1一样,但偏心碰不发生大部分动量交换,碰撞导致颗粒1和2以一定的速度向右运动;同时,颗粒2发生旋转。由于旋转速度的不同,两者的角位移发生一定的偏差。
从图2(b)可见:
1) 颗粒1只有一部分动量传递给颗粒2,自己保留了一部分。颗粒2发生平动和转动,同时获得了
Table 1. Calculated parameters
表1. 计算参数
Table 2. Operating conditions
表2. 工况参数
 (a)
(a)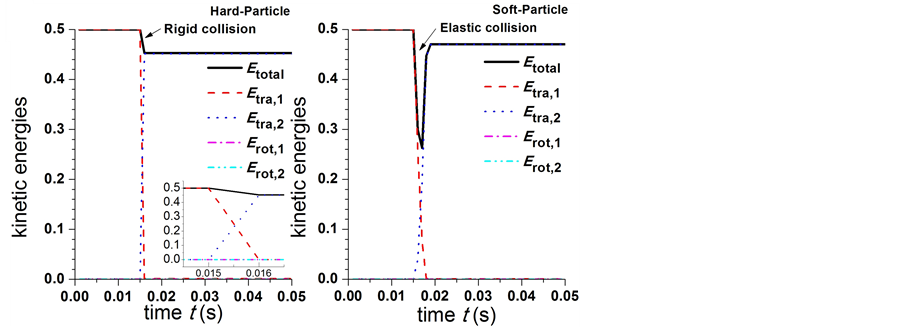 (b)
(b)
Figure 1. A pair of triangular particles before and after the central collision (a) and related variation of energy (b)
图1. 颗粒对心碰撞前后(a)及能量关系(b)
转动和平动动能;
2) 颗粒1大部分平动动能损失转换为颗粒2的转动动能增量和平动动能增量;
3) 硬颗粒和软颗粒模型的模拟结果出现小幅偏差,其主要原因在于:① 硬颗粒模拟结果中颗粒2的转动动能增量要大于平动动能增量,而软颗粒模拟结果中颗粒2的平动动能增量要大于颗粒2转动动能增量;② 硬颗粒模拟结果中颗粒1的动能损失比软颗粒模拟结果中的动能损失要小。
 (a)
(a)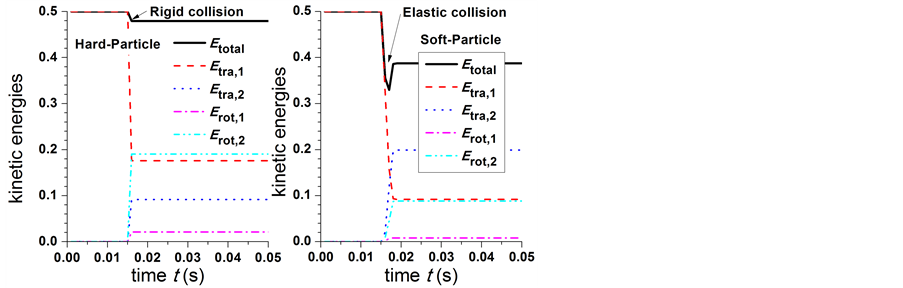 (b)
(b)
Figure 2. A pair of triangular particles before and after the off center collision (a) and related variation of energy (b)
图2. 颗粒偏心碰撞前后(a)及能量关系(b)
那么,在上面的模拟中,哪个结果更符合实际呢?我们认为两者皆有可能,取决于颗粒的质量分布:1) 对于颗粒转动惯量较大,而质量较小的几何体(即质量分布偏向颗粒几何的边界上),颗粒所受之表面力,将更易于使颗粒在碰撞中增加平动动能,更难增加转动动能;2) 反之,对于颗粒转动惯量较小,质量分布偏向质心,颗粒在碰撞中将更多地增加颗粒的转动动能而较小地增加平动动能。因此,对于软颗粒SIPHPM模型,颗粒质量分布于颗粒的几何边界上,即属于第1)种情形;而对于硬颗粒GHPM模型,颗粒质量均匀分布于颗粒几何,相对来说属于第2)种情形。因此,SIPHPM模型计算的结果,颗粒在偏心碰撞中增加的平动动能多于转动动能,反之,对于GHPM模型计算的结果,颗粒在偏心碰撞中增加的转动动能多于平动动能。
4. 结论
本文对GHPM模型和SIPHPM模型模拟典型非球形颗粒碰撞过程进行了比较分析。得出了如下结论:
1) 对于对心碰撞过程,GHPM和SIPHPM都能够准确预测颗粒碰撞动力学过程,获得近乎相同的颗粒碰撞后的速度;
2) 对于偏心碰撞过程,GHPM和SIPHPM都在原则上能够获得颗粒碰撞后的平动速度和角速度。但碰撞过程中对于平动速度和角速度变化量的分配则受颗粒质量分布的影响。硬颗粒模型认为颗粒质量均匀分布,偏心碰撞过程中转动动能变化占主导;SIPHPM模型认为大部分颗粒质量分布于颗粒边界,偏心碰撞过程中平动动能变化占主导;
3) 从能量分析的角度看,两者均严格符合由恢复系数定义的碰撞能量变化规律;微观上,SIHPM软颗粒模型在碰撞过程中会发生动能和弹性形变势能的相互转化,使得瞬时颗粒体系的动能会出现波动。
文章引用
吴达岭,桂 南. 非球形颗粒碰撞过程硬颗粒与软颗粒模型比较研究
Comparison of Collision Dynamics of Non-Spherical Particles between the Hard-Particle Model and Soft-Particle Model[J]. 应用物理, 2017, 07(04): 97-102. http://dx.doi.org/10.12677/APP.2017.74014
参考文献 (References)
- 1. 桂南. 复杂两相流动中颗粒碰撞的DEM-LES/DNS耦合模拟研究[D].杭州: 浙江大学, 2010.
- 2. Hoomans, B.P.B., Kuipers, J.A.M., Briels, W.J. and van Swaaij, W.P.M. (1996) Discrete Particle Simulation of Bubble and Slug Formation in a Two-Dimensional Gas-Fluidised Bed a Hard-Sphere Approach. Chemical Engineering Science, 51, 99-118.
- 3. Hoomans, B.P.B. (1999) Granular Dynamics of Gas-Solid Two-phase Flow. Ph.D. Thesis, Netherlands: Maastricht, 146-149.
- 4. Cundall, P.A. and Strack, O.D.L. (1979) A Discrete Numerical Model for Granular Assemblies. Geotechnique, 29, 47-65. https://doi.org/10.1680/geot.1979.29.1.47
- 5. Crowe, C.T., Sommerfeld, M. and Tsuji, Y. (1998) Muhiphase Flow with Droplets and Particles. CRC Press, New York.
- 6. Gui, N., Yang, X.T., Tu, J.Y. and Jiang, S.Y. (2016) An Extension of Hard-Particle Model for Three-Dimensional Non-Spherical Particles: Mathematical Formulation and Validation. Applied Mathematical Modelling, 40, 2485-2499.
- 7. Gui, N., Yang, X.T., Tu, J.Y. and Jiang, S.Y. (2016) A Soft-Sphere-Imbedded Pseudo-Hard-Particle Model for Simulation of Discharge Flow of Brick Particles. AIChE Journal, 62, 3562-3574. https://doi.org/10.1002/aic.15278
