Applied Physics
Vol.
13
No.
12
(
2023
), Article ID:
76938
,
7
pages
10.12677/APP.2023.1312055
分光计测三棱镜顶角和折射率的简化与改进
赵亚运*,李方犁
广东理工学院智能制造学院,广东 肇庆
收稿日期:2023年11月3日;录用日期:2023年12月5日;发布日期:2023年12月12日

摘要
用分光计测量三棱镜的顶角和折射率是大学物理中非常重要的一个光学实验,但因为实验原理复杂,光路调节要求高以及实验操作难度大等原因,往往导致实验过程繁琐冗长,整体实验完成度不高。本文总结分析了实验中可能出现的问题及原因,并创新提出了“双平行微调法”、“双垂直顺转法”分别对测三棱镜顶角和折射率进行简化改进。研究可提高学生实验完成率,也可为教师教学提供参考。
关键词
分光计,三棱镜顶角,折射率,双平行微调法,双垂直顺转法

Simplified and Improved Measurement of Prism Apex Angle and Refractive Index Using a Spectrometer
Yayun Zhao*, Fangli Li
Intelligent Manufacturing Institute, Guangdong University of Technology, Zhaoqing Guangdong
Received: Nov. 3rd, 2023; accepted: Dec. 5th, 2023; published: Dec. 12th, 2023

ABSTRACT
The measurement of the apex angle and refractive index of a prism using a spectrometer is a critically important optical experiment in university physics. However, due to the complex experimental principles, high demands for optical path adjustments, and the overall difficulty of experimental operations, the experiment often becomes cumbersome and time-consuming, resulting in a relatively low overall completion rate. This paper summarizes and analyzes potential issues and their causes in the experiment, and innovatively proposes the ‘Dual Parallel Micro-adjustment Method’ and the ‘Dual Vertical Sequential Rotation Method’ to simplify and improve the measurement of the prism’s apex angle and refractive index. The research aims to enhance the completion rate of student experiments and provides valuable references for teaching staff.
Keywords:Spectrometer, Prism Apex Angle, Refractive Index, Dual Parallel Micro-Adjustment Method, Dual Vertical Sequential Rotation Method

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
分光计是一种重要的光学仪器,可以精确的测量光线的偏转角,在大学物理实验中应用非常广泛。在用分光计的物理实验中,测量三棱镜的顶角和折射率是其中操作相对复杂,难度较大的实验。该实验主要由两大部分组成:一是,用自准法测量三棱镜的顶角。二是,用最小偏向角法测量三棱镜的折射率。然而,在预习不充分、实验课时有限的情况下,学生很难完成实验因此,本文针对两部分实验各自的重难点,从原理、步骤及数据处理三个方面进行简化与改进,便于学生更好的理解和操作实验,同时也为教师教学提供参考。
2. “双平行微调法”测量三棱镜的顶角
测量三棱镜顶角的实验原理简单容易理解,但因为实验对于光路的调节要求较高,教材中普遍采用的自准法在具体实验操作过程中既繁琐又易出错,因此本文将采用“双平行微调法”,该方法能高效的找到反射叉丝,确定透光面法线位置从而求得偏转角,进而计算出三棱镜的顶角。
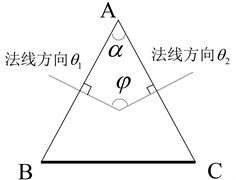
Figure 1. Top view of a prism
图1. 三棱镜俯视图
使用分光计测三棱镜的顶角时,所需要调节的地方主要是载物台和分度盘,而对应的原理是光的反射。如图1是三棱镜的俯视图,其中AB和AC面是光滑的透光面,BC面是粗糙的不透光面,需要测量的顶角即为AB和AC两个透光面组成的夹角 。测顶角 的主要原理是让绿色“十”字光源从两个透光面垂直入射找到各自的反射叉丝,记录垂直入射光的位置(即图1中法线所在位置),利用几何原理即可算出三棱镜的顶角。而实验操作过程中最常见的几个问题如下:一是,不能找到与透光面垂直入射的反射光,从而确定图1中的法线方向 和 ;二是,不能准确的读数;三是,公式的简化问题。
2.1. “双平行微调法”的使用
找到入射光在三棱镜透光面的反射绿色“十”字叉丝是测量三棱镜顶角实验的核心步骤。该步骤实验的成功需要注意两个方面的问题。一是,仪器的调节问题。二是方法的使用问题。
在仪器的调节问题上,要注意两个关键点。第一个关键点,望远镜的焦距(自准直法)。将透光面贴在望远镜筒上(此时入射光一定与透光面垂直),只需要调节目镜视度调节手轮看到清晰明亮的反射叉丝即可锁定望远镜锁紧螺丝,目镜的焦距便调节完毕,后续过程无需再次调节。第二个关键点,载物台水平。在三棱镜透光面贴紧望远镜调好焦距可以看到反射光叉丝的基础上,三棱镜置于载物台上始终看不到反射叉丝,或者只看到一个透光面的反射叉丝。此时,大概率是载物台不水平的所造成,当三棱镜朝某个方向倾斜,根据反射原理很难同时找到两个透光面入射光的反射光叉丝。

Figure 2. Front view of spectrometer
图2. 分光计正视图

Figure 3. Top view of telescope and prism
图3. 望远镜和三棱镜俯视图
在方法的使用问题上,采用“双平行微调法”。找到置于载物台上三棱镜的两个透光面反射光的叉丝也是该部分实验最难的地方,盲目的转动望远镜或上下调节镜筒不仅耗费时间,还会让实验产生更多的不确定性。而采用“双平行微调法”可以更加高效、准确的找到反射的绿色“十”字叉丝。所谓的“双平行微调法”,第一个平行是指将望远镜镜筒与水平的横梁平行,如图2分光计正视图中的红色虚线所示;第二个平行是指将望远镜的横切面与AB的透光面平行,如图3望远镜和三棱镜俯视图中的红色虚线所示。在操作中,可将实验简化成在调好焦距和载物台水平后,将三棱镜置于载物台上,锁定分度盘与望远镜固联螺丝,将望远镜镜筒转到三棱镜透光面AB方位处,采用“双平行微调法”让叉丝位于背景分划板的中心,此时AB面的法线位置记 ;同理操作,可以找到AC面对应的法线位置,记为 ;然后再来回转动记录三组数据。“双平行微调法”实用、效率高,能够帮助学生很快完成第一部分的实验。
2.2. 读数对应问题
入射光的这条直线与游标盘分度盘有两个交点,对应表盘上的两个读数位置,故每次读数需要同时读两个数据,即AC面时的 和 ,AB面时的 和 ,且满足 ,理论上正常读数误差不会超过1度。而分度盘和游标盘的读数与游标卡尺读数方法类似,分度盘相当于游标卡尺的主标尺,游标盘当于副标尺,而将主标尺的0.5˚ = 30'分为副标尺30格,故最小分度值为1',按照游标卡尺基本读数方法(副尺0对应主尺的整毫米数 + 主尺与副尺对齐的格子数 × 最小分度值)读数即可。
2.3. 公式的简化问题
实验教材上顶角的计算公式 ,而 ,所以 。然而在实验操后的计算过程中经常遇到原本60˚左右的顶角用公式有时算出来的却是在120˚左右。这里由于分度盘上0˚的位置也是360˚的位置,若望远镜偏转的角度包含360˚,则此时偏向角表达式应该为 ,带入简化则对应三棱镜顶角 。因此,总结这两种情况,如果最后测得的法线位置代入公式算出来的顶角满足 ,即可证明该部分实验的成功。
3. 最小偏向角法测量三棱镜的折射率
用分光计测三棱镜的折射率相对于测顶角来说在原理和操作方面都更为复杂,学生更容易出错。测量三棱镜折射率的方法也比较多,如用临界法测量三棱镜的折射率 [1] 、垂直折射法测量三棱镜的折射率 [2] 和全反射法测量三棱镜的折射率 [3] 等。和以上方法比较而言,用最小偏向角法测三棱镜的折射率,优点是数据的准确度比较高,结果符合性强,不确定度较低 [4] 。缺点是实验原理公式理解困难和实验操作相对繁琐。本文用两个“垂直顺转法”对最小偏向角法进行了改进,能快速找到折射光并确定最小偏向角的位置,进而更方便算出最小偏向角。
3.1. 最小偏向角测折射率原理
当入射光从三棱镜的一个透光面穿入,然后从另一个透光面折射出来时,入射光和折射光的夹角称为偏向角 ;而随着入射光入射角度的变化, 也随之变化,且在变化过程中存在最小值 ,称为最小偏向角。利用该特点和折射率定义公式可以得到折射率n与 的关系式为:
因此,通过实验操作得到实验数据,然后算出 ,结合第一部分实验测量计算出来的三棱镜顶角 即可算出三棱镜的折射率。在这部分实验中通常存在以下几个问题:一是,折射率n与 的关系公式是如何推导出来的。二是,实验操作过程中如何快速找到最小偏向角对应折射光的位置。三是,如何确定自己最终折射率计算的准确度。
证明最小偏向角公式的方法有很多,例如用几何方法 [5] 、求导法 [6] 和拉格朗日中值法 [7] ,也可以利用光的折射定律以及光在三棱镜中折射的三角关系证明 [8] ,还可以用初等数学计算 [9] 、不等式极值法和借用Matlab、Mathematic等软件处理。因此,在教材给定不完整的情况下可以简单给学生提供一些证明思路,可以帮助学生更好的理解实验。
3.2. “双垂直顺转法”的使用
找到折射光以及确定最小偏向角的位置即为该部分实验的核心。在实验的过程中,学生找不到折射光或者将折射光夹角误认为最小偏向角是该部分实验最为常见的问题。因此,不仅需要教学生实验的原理和步骤,还需要让学生用正确且简单的方法和步骤去完成实验。因此,本文采用“双垂直顺转法”解决以上难题,“双垂直顺转法”中的第一个“垂直顺转”即望远镜与AC面垂直,顺时针转动望远镜;第二个“垂直顺转”即入射光与AB面垂直,顺时针转动载物台。通过“双垂直顺转法”可以帮助学生精准快速找到反射光和确定最小偏向角。
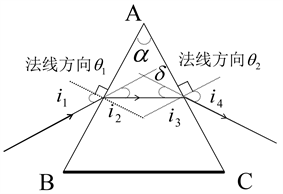
Figure 4. Principle of minimum deviation angle
图4. 最小偏向角原理
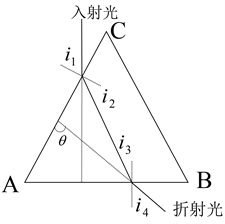
Figure 5. Geometric ray
图5. 几何光线
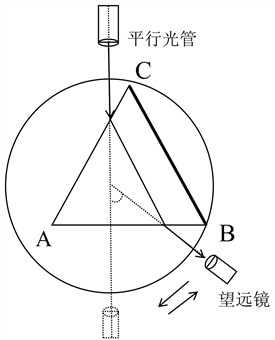
Figure 6. Measure the minimum deviation angle
图6. 测量最小偏向角
如图4所示,AB面的入射角和折射角分别为 、 ,AC面的分别为 、 ,入射光和出来的折射光延长线(虚线)的夹角 即为偏向角,由折射定律可知 , 。根据几何角度的关系易得 ,再结合与已知顶角 的关系,可以证明最小偏向角与折射率的关系。在有限的2个课时内,为保证实验顺利的完成,很难直接在课堂给学生进行公式的证明且让学生理解,因此,适当采用一些概括性高、简练而具有记忆点的步骤方法,可以让学生实验更有目标性,从而快速且正确的完成实验。从结论出发可知当偏向角 取最小值时, 且 ,即当通过三棱镜的光线与三棱镜底面BC平行时取最小偏向角 。通常实验室采用的三棱镜其横截面为正三角形,因此 ,而三棱镜的折射率大约为1.648,则入射角 ,即当入射角在55.5˚左右时通过三棱镜的光路偏向角达到最小值。
“双垂直顺转法”中的第一个“垂直顺转”。如图5所示的几何光路图,令三棱镜折射率的真值为1.65,当入射光与AB面垂直时,在AC面的入射角 为60˚,根据折射定律计算折射角 为31.67˚;同理,利用几何关系可以推出AB面的入射角 为28.33˚,算出折射角 为51.53˚,则从三棱镜出来的折射光与AC面的夹角 为81.32˚,小于90˚。因此为了快速找到折射光位置,可将三棱镜如图5放置(入射光与AB面垂直),望远镜调至与AC面垂直,再缓慢顺时针转动望远镜即可找到折射光,此为第一个“垂直顺转”。
“双垂直顺转法”中的第二个“垂直顺转”。如图6所示,当平行光管垂直AB面(入射光与AB面垂直)时,此时入射角为60˚小于最小偏向角所对应的入射角,故在用第一个“垂直顺转法”找到折射光后,只需顺时针旋转载物台,此为第二个“垂直顺转”。通过操作就可以在望远镜中看到折射光朝一个方向平移,出现回转的地方即为最小偏向角所在位置。
3.3. 读数测量问题
在确定最小偏角所在位置后,先要记录此时游标1和游标2的读数 和 ;其次,取下载物台上的三棱镜,找到入射光的位置记录此时游标1和游标2的读数 和 。最后根据教材给出的最小偏向角公
式 ,即可算出最小偏向角。通常其中 和 约为51˚的锐角,但由分
度盘上0˚的位置也是360˚的位置,所以计算出来的结果也可能是最小偏向角的补角约为309˚。因此若 和 为钝角,则取其补角带入上式求最小偏向角,然后根据最小偏向角与折射率的关系式计算出三棱镜的折射率。
4. 总结
用分光计测三棱镜的顶角和折射率是大学物理中比较经典的实验,但是该实验耗时长且容易出错。本文对实验中的容易出错的问题进行了归纳总结,并对实验中要注意的细节问题进行了补充提示。除此之外,还创新性的提出了用“双平行微调法”、“双垂直顺转法”分别对测三棱镜顶角和折射率进行简化改进。“双平行微调法”避免了实验的繁杂和冗长,能使学生快速从望远镜里面看到绿色的反射叉丝,提高了观测的成功率;“双垂直顺转法”可帮助学生快速精准找到反射光和确定最小偏向角。本文可为学生的实验操作和教师的实验教学提供参考和帮助。
文章引用
赵亚运,李方犁. 分光计测三棱镜顶角和折射率的简化与改进
Simplified and Improved Measurement of Prism Apex Angle and Refractive Index Using a Spectrometer[J]. 应用物理, 2023, 13(12): 527-533. https://doi.org/10.12677/APP.2023.1312055
参考文献
- 1. 张洁, 李成龙. 临界法测三棱镜的折射率[J]. 科技信息, 2008(31): 184.
- 2. 朱德权. 垂直折射法测三棱镜的折射率[J]. 安庆师范学院学报(自然科学版), 2007(4): 74-76.
- 3. 高雁, 康德胜, 刘永庆. 全反射法测三棱镜折射率的相图研究[J]. 大学物理实验, 2019, 32(2): 34-36.
- 4. 周凯宁, 肖宁, 陈棋, 钟杰, 李登峰. 3种测量三棱镜折射率方法的对比[J]. 实验室研究与探索, 2011, 30(4): 22-25+90.
- 5. 弓斌耀, 赵玉怀. 最小偏向角条件的几何证明[J]. 榆林高等专科学校学报, 1999(2): 34-35.
- 6. 王艳文, 蔡晓燕. 三棱镜最小偏向角公式的推导[J]. 科技创新导报, 2012(3): 226.
- 7. 罗乐, 何于江. 由拉格朗日中值定理推导三棱镜的最小偏向角[J]. 物理通报, 1997(4): 5-6.
- 8. 张志强, 张瑞瑞, 赖晓磊, 杨铁柱. 三棱镜最小偏向角公式的一种证明方法[J]. 科技创新导报, 2013(28): 177+179.
- 9. 李广荣. 用初等数学证明棱镜的最小偏向角公式[J]. 物理通报, 1965(2): 59-60.
NOTES
*通讯作者。