Material Sciences
Vol.
10
No.
02
(
2020
), Article ID:
34180
,
9
pages
10.12677/MS.2020.102012
Analysis Method of Pore Size Distribution of Porous Materials
Lixia Bao, Peifeng Gao, Shaochun Peng
Analysis and Testing Center, Beijing Institute of Technology, Beijing

Received: Jan. 22nd, 2020; accepted: Feb. 6th, 2020; published: Feb. 13th, 2020

ABSTRACT
Pore size and pore size distribution are one of the important properties of porous materials. Various theoretical models for pore size analysis, including Barrett-Joyner-Halenda (BJH), Horvath-Kawazoe (HK), Saito-Foley (SF) and NLDFT (non-local density functional theory) are introduced, and the applicable conditions of each theoretical model are summarized. The results show that BJH method can be used to analyze cylindrical mesoporous materials with pore size between 5 nm and 50 nm. HK method is more suitable for the analysis of microporous activated carbon materials with slit holes, and SF method is intended for analyzing cylindrical microporous materials according to the adsorption isotherms determined by argon. NLDFT method is more suitable for the analysis of micro-mesoporous composites, which has a wide range of applications and prospects.
Keywords:Pore Size Distribution, Porous Materials, BJH, HK, SF, NLDFT

多孔材料孔径分布测试方法的研究
暴丽霞,高培峰,彭绍春
北京理工大学分析测试中心,北京
收稿日期:2020年1月22日;录用日期:2020年2月6日;发布日期:2020年2月13日

摘 要
孔径及孔径分布是多孔材料的重要性质之一,通过介绍包括Barrett-Joyner-Halenda (BJH)法、Horvath-Kawazoe (HK)法、Saito-Foley (SF)法和NLDFT (非定域密度泛函理论)多种孔径分析的理论模型,总结了每种模型的优缺点及适用条件。结果表明,BJH法只能适用于分析柱状的介孔材料(5 nm < 孔径 < 50 nm);HK法只适用于分析含狭缝孔的微孔活性炭材料;SF法适用于根据氩气吸附等温线分析圆柱型微孔材料;NLDFT法不仅适用于分析微孔材料的孔径分布,还可以分析微介孔复合材料孔径分布,具有更广的应用范围及前景。
关键词 :孔径分布,多孔材料,BJH,HK,SF,NLDFT

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
多孔材料是指具有一定尺寸和数量的孔隙结构的材料,按照孔隙的开放程度可以分为闭孔和开孔。近些年研究较多的多孔材料主要有分子筛、活性炭、陶瓷材料和有机高分子材料(MOF和COF)等。纳米多孔材料在催化和分离上已经得到广泛应用 [1] [2] [3] [4] [5],另外在光电转化 [6] 、电磁学应用领域也得到了发展 [7] [8] [9]。
孔径分布是表征多孔材料很重要的一个参数。依据国际纯粹和应用化学联合会(IUPAC)的定义,根据多孔固体材料孔径(d)的大小可以把多孔材料分为三种类型:微孔材料(d < 2 nm),介孔材料(2 nm < d < 50 nm)和大孔材料(d > 50 nm)。容量法气体吸附法是孔径分析必不可少的手段,是在恒定温度下通过连续收集不同压力下材料吸附气体的体积,最终形成压力–体积的吸附等温线,并在假设的或理想化的材料孔型基础上对等温线进行后期数学分析,从而推算出孔径分布的复杂分析方法 [10]。若要保证孔径分析结果的准确性,首先要保证吸附等温线测定的准确性,其次,还需要使用者根据样品孔形和理论模型特点来综合分析多孔材料的孔径分布。因此,需要对孔径分析的理论模型有清楚的理解,才能针对不同样品选择合适的分析方法。现有文献中孔径分析模型的选择几乎都是千篇一律的,介孔材料用BJH法分析,微孔材料用HK或者DFT分析,缺乏根据材料特性选择合适模型的研究,导致孔径分析的误差有所提高。
本文从理论基础、适用条件、应用实例等方面介绍孔径分析的各个理论模型,并且探讨如何根据多孔材料选择合适的模型分析孔径。该研究可以为多孔材料孔径分析模型的选择提供选择依据,有利于减小分析误差。
2. 介孔材料孔径分析方法
Barrett-Joyner-Halenda (BJH)方法基于Kelvein和Halsey方程,是最早确定孔径分布的方法之一。Kelvin方程以热动力学为基础,方程形式如下 [11]
(1)
P是液体在半径为r的微孔中的平衡蒸汽压,P0是液体的饱和蒸汽压力,γ和 分别是液体的表面张力和摩尔体积,θ是液体在微孔中的接触角。r是Kelvin半径或者临界半径,不是微孔的真正半径,假设发生凝聚时吸附层厚度为t,则微孔的真正孔半径可表示为
(2)
t由Halsey方程确定,
(3)
是单吸附层厚度。当吸附质为氮气时, ,带入(3)即可得到吸附层厚度与压力的平衡关系式:
(4)
方程(1)、(2)和(4)是BJH方法计算孔径分布(PSD)的基本方程。
BJH法是应用Kelvin方程通过简单的几何计算分析孔径的经典方法,它假设孔型是圆柱孔,仅适用于指定的孔径范围并且低估了孔径,容易导致重大偏差(孔径 < 5 nm时,偏差可达25%),主要适用于大于5 nm的介孔柱状模型 [12]。ISO15901《固体材料孔径分布与孔隙率的压汞法和气体吸附法测定–第2部分:气体吸附法分析介孔和宏孔》对BJH的使用提出了明确的限定条件:1) 孔隙是刚性的,并且有规则的形状(比如,圆柱状);2) 不存在微孔;3) 孔径分布不连续超出此方法所能测定的最大孔隙,即在最高相对压力处,所有测定的孔隙均已被充满。
根据GuohuiCai等人 [13] 的条件制备的有序介孔氧化铝材料,采用BJH法进行孔径分析,结果如图1所示。
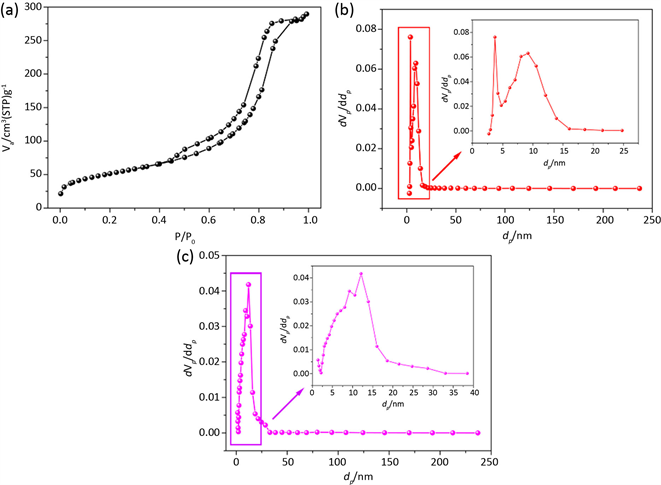
Figure 1. BJH Pore Size Distribution (PSD) of Alumina (a-Adsorption Isotherm; b-PSD by Adsorption Branch; c-PSD by desorption Branch)
图1. 氧化铝BJH法孔径分析图(a-氧化铝的吸脱附等温线;b-BJH法吸附支孔径分布图;c-BJH法脱附支孔径分布图)
图1(a)是粉末状多孔氧化铝的吸附等温线,其中存在明显的回滞环,说明该氧化铝材料含有介孔。根据回滞环的形状可知,该材料具有比较窄的孔径分布,而且孔型基本属于圆柱型孔。图1(b)是利用吸附等温线的吸附支进行分析。从图中的分析结果也可以印证,该粉末氧化铝具有较窄的孔径分布,孔的大小主要集中在12 nm左右,这与文献中材料 [13] 的孔径比较符合。图1(c)是利用吸附等温线的脱附支进行BJH分析,从图中可以看出,材料孔径分布除了在10 nm左右有一个明显的峰以外,在4 nm左右还有一个很尖锐的峰。结合吸附等温线形状及吸附支BJH法进行孔径分析的结果,我们可以得知,利用脱附支进行BJH分析时,4 nm左右的峰是不准确的。这就是应用BJH另一个非常严重的问题即在脱附曲线上出现假峰,这个假峰的位置非常固定,77 K下的氮吸附孔分布基本在4 nm左右,造成假峰的原因主要有多孔材料内部孔道的连通性、孔型的多样性以及孔径的分散性等 [14]。
根据BJH理论模型的原理及应用实例分析,可知BJH法适用于圆柱型介孔材料孔径分析,并且要采用吸附支进行分析,对于孔径大于5 nm的介孔材料,分析结果更为准确。
3. 微孔材料孔径分析方法
在孔径小于2 nm的微孔材料中,孔壁间的相互作用势能相互重叠,微孔的吸附比介孔强大,在相对压力P/P0 < 0.01时,就会发生微孔中的填充,孔径在0.5~1 nm的孔甚至在相对压力10−5~10−7时即可产生吸附质的填充,所以微孔的测定与分析比介孔要复杂的多。
BJH方法可应用于孔径大于5 nm的介孔材料孔径分析,但不适用于微孔填充的描述 [15] [16]。主要原因在于,其一,Kelvin方程在孔径小于2 nm时是不适用的;其二,毛细凝聚现象描述的孔中的吸附质为液态,而在微孔中,由于密集孔壁的交互作用,使得填充于微孔中的吸附质处于非液态状态。因此,BJH法不再适用于微孔孔径分析。
针对微孔材料孔径分析的理论模型,由1951年发展的T图模型开始,随后出现了DR模型、MP模型、DA模型、HK模型、SF模型以及到1993年发展起来的DFT模型。这些理论模型中,t-图法和DR法是介孔分析的一种外推,只能推出微孔的总孔体积,不能进行孔径分析。这些方法没有脱离介孔分析的基本假定,孔径与压力的对应关系仍采用Kelvin方程,孔内凝聚氮的密度仍采用液氮的密度,因此这两种分析方法不是适用于微孔材料。MP法和DA法虽然能够得出微孔孔径分布,但是结果十分粗糙且不可靠,分析的孔径范围也十分有限,因此,应用价值不大。现在微孔材料孔径分析,最常用的分析方法是Horvath-Kawazoe (HK)法和Saito-Foley (SF)法。
3.1. Horvath-Kawazoe (HK)法
HK法 [17] 是一种由微孔上样品氮吸附等温线计算有效孔径分布的半经验分析方法。该方法假设材料为狭缝孔(这些孔多出现在炭分子筛和活性炭内)。Horvath和Kawazoe通过热力学讨论,发现平均势能与吸附的自由能变有关,得出了微孔内吸附能与有效孔径之间的关系:
(5)
其中,K为阿伏伽德罗常数, 为吸附剂每单位面积上的原子数。
(6)
为吸附质每单位面积上的分子数,m是电子的质量,c为光速, 是吸附剂的极化率, 是吸附质的极化率, 是吸附剂的磁化率, 是吸附质的磁化率。
(7)
(8)
是吸附剂分子的直径, 是吸附质分子的直径,l是吸附剂上两层吸附质之间的距离, 由式(5)可以看出对于某一给定尺寸和形状的微孔会在某一特定相对压力下发生微孔填充,该特征压力直接与吸附剂–吸附质相互作用有关。
从HK法的原理可以得出,利用HK法分析微孔材料孔径分布是有一定前提条件的:1) 须是微孔材料基于N2在液氮温度(273.15 K)下的吸附等温线;2) 微孔材料是炭分子筛和活性炭类样品;3) 假设孔型为狭缝孔。
图2是微孔炭材料的孔径分析结果,图2(a)是炭材料的吸脱附等温线,从图中可以看出,在P/P0 < 0.01时,有一个很快的吸附,说明材料主要是微孔结构,在P/P0接近1的时候,吸附曲线有向上的一个吸附量,说明含有少量的堆积大孔。图2(b)是HK法分析的孔径结果,从图中可以得出,该材料的孔径主要分布在0.5 nm左右。
HK法适用于狭缝孔微孔炭材料,根据液氮温度下的氮气吸附等温线进行孔径分析,分析结果也更接近于实际数值。将该法应用于沸石分子筛微孔孔径分析中,是错误的。
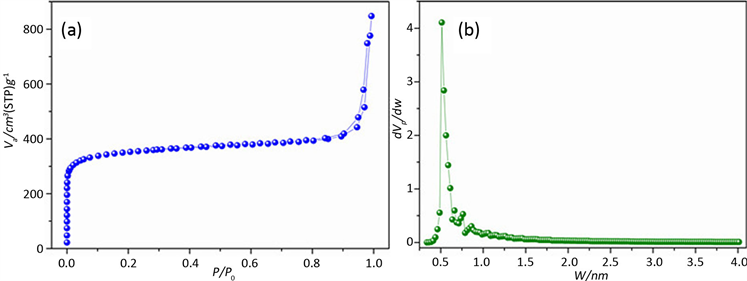
Figure 2. PSD of Carbon Matirial by HK (a-Adsorption Isotherm; b-PSD by HK)
图2. HK法分析炭材料的孔径分布(a-吸附等温线,b-HK法孔径分布)
3.2. Saito-Foley (SF)法
Saito和Foley将HK法扩展到由氩87 K时在沸石分子筛上的吸附等温线计算有效孔径分布。Saito和Foley (SF)法同样基于Everett和Powl势能方程,假设孔型为圆柱形。HK对数运算式,Saito和Foley导出一类似于HK方程的关系式,其将微孔填充的相对压力与(有效)孔径 相关联。
(9)
(10)
参数 和 的定义如式(2.8)和(2.9)所示:
(11)
(12)
为了对HK法和SF法进行计算,需要知道吸附剂参数 、、、 以及吸附质参数 、、、 的数值,这些参数的选择对运算结果影响很大。
根据SF法的理论,该法适用于圆柱形微孔沸石分子筛基于氩气吸附等温线的孔径分析。
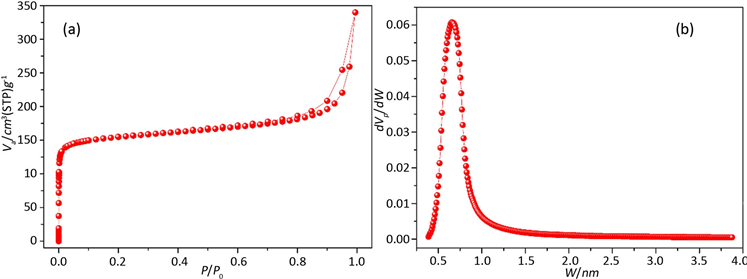
Figure 3. PSD of Zeolite by SF (a-Adsorption Isotherm; b-PSD by SF)
图3. SF法分析沸石分子筛孔径分布图(a-沸石分子筛吸附等温线,b-SF法孔径分布图)
图3是沸石分子筛的孔径分析图,图3(a)是沸石分子筛的吸附等温线,从图中可以看到该沸石分子筛在P/P0 < 0.01时已经完成了微孔填充,之后有吸附量基本上没有增加,在P/P0接近1的时候,吸附量有一个上升的趋势,可以得知该材料有一些堆积形成的大孔,但并不多。图3(b)是用SF法分析材料的孔径分布图,从分析结果可知,该沸石分子筛的主要孔径集中在0.652 nm。从图3可以看出,用SF法分析沸石分子筛孔径分布能够得出完整的一个孔径分布峰形,分析结果比较准确。
4. 微介孔材料孔径分析方法
经典的孔径分析理论,如BJH、HK和SF等属于宏观热力学方法,大量的理论和实验工作表明,受限流体的热力学性质与自由流体有相当大的差异,如临界点、冰点和三相点的位移等 [18] [19] [20] [21],这就导致了宏观热力学的分析方法存在较大的误差。
针对宏观热力学方法的不足,从上世纪90年代开始推出微观分析方法,是基于在分子水平上描述被吸附分子状态的统计力学方法,用统一方法在整个孔径分布范围内准确进行孔径分析,真实地反应多孔材料的孔中流体热力学性质。由Neri-mark等人 [22] 创立的非定域密度泛函理论(NLDFT法),从分子水平上描述了受限于孔内的流体的行为,其应用可将吸附质气体的分子性质与它们在不同尺寸孔内的吸附性能关联起来,因此,NLDFT法适用于微孔和介孔的全范围孔径分析。
微观分析法认为,气体分子被吸附于孔中,并不是以均一的液态存在的,而是介于液态和气态之间的某种状态,而且孔中吸附质的密度是不均匀的,靠近孔壁处密度接近气态,靠近孔心处密度接近于液态,而且密度随距离的变化是波动的。
图4的密度分布图清晰地指出孔凝聚本来就存在于孔的核心区,这导致在较大的介孔(孔宽为20个分子直径)中生成似乎无约束的核心液体,就像在孔的核心区一样;孔中吸附质的密度分布与孔径、压力以及吸附质与吸附剂的相互作用有关。微观分析方法在分子的水平上描述受限于微孔中的流体结构,把吸附质气体的分子性质与他们在不同尺寸孔内的吸附性能关联起来。
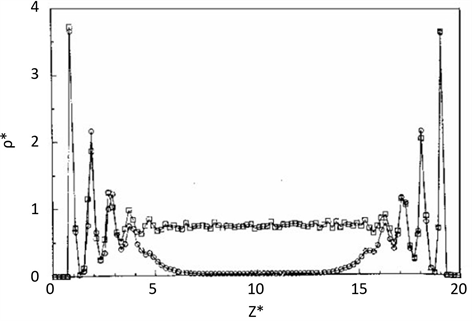
Figure 4. Density distribution of coexisting gas (spherical) and liquid (square) in 20 molecular diameter fracture pores [21]
图4. 在孔宽为20个分子直径的裂隙孔中共存气体(球形)和液体(方形)的密度分布图 [21]
NLDFT法假设吸附等温线是由无数个别的“单孔”吸附等温线乘以它们的覆盖孔径范围的相对分布得到的。只要给定吸附质/吸附剂的体系,就能通过DFT或MC模拟得到一组等温线(也叫Kernel,即核心文件或影响函数),通过快速负数最小二乘法解方程就能推导出孔径分布曲线。NLDFT可以比较实验等温线和计算等温线,对等温线的拟合非常好,则表明反映孔径状态准确。用于碳、二氧化硅、沸石等各种材料类型的不同孔模型已经开发并且得到广泛应用(例如,狭缝孔、筒型孔和球形孔以及混合孔形)。
在运用NLDFT分析孔径时,要注意模型的选择与以下因素或者条件匹配:1) 吸附气体/吸附温度;2) 材料类型;3) 孔型假设。如果假设的孔型反推计算得到的拟合误差足够小,则说明孔型选择正确;否则,需要再尝试另一个孔型进行拟合误差比较。
图5是微介孔碳材料的孔径分析图。从图5(a)的吸附等温线可以看出,材料在相对压力P/P0小于0.01时,有一个很明显的快速吸附,而且在P/P0 = 0.4~0.8之间有一个明显的回滞环,这些可以说明该炭材料是微介孔复合材料,在P/P0接近1的地方,等温线不是趋于平坦的,而是有向上的吸附,说明材料中有少量的大孔存在。从图5(b)可知,微孔孔径大约为0.6 nm左右,介孔孔径为2.4 nm左右,没有大孔存在,说明该方法分析的孔径结果是不太准确的。由图5(c)的NLDFT分析结果可以得知,炭材料的微孔为1.6 nm左右,介孔约为4.84 nm,另外,在15 nm、45 nm处也有峰,该处主要是堆积孔,另外,在65 nm左右也有一个小峰,这些峰的存在证明该材料具有少量的大孔存在。依据NLDFT方法分析的孔径分析结果,跟实际测得的吸脱附等温线比较符合,说明该方法分析的孔径分析结果比较准确。
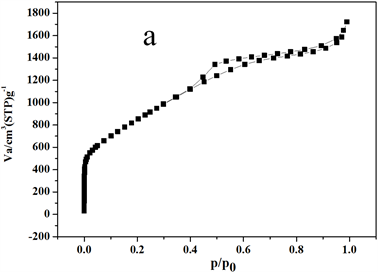
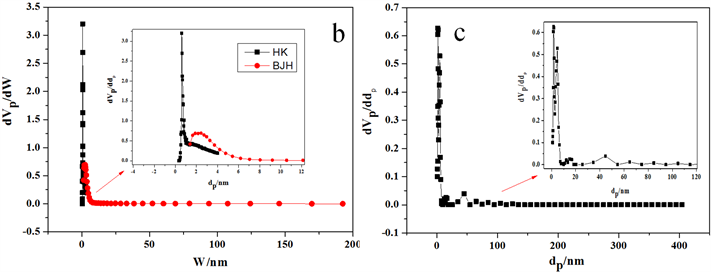
Figure 5. PSD of micro-mesoporous carbon materials (a-Adsorption Isotherm; b-BJH-HK method; c-NLDFT method)
图5. 微介孔炭材料孔径分布图(a-炭材料吸附等温线;b-BJH和HK法联合分析孔径图;c-NLDFT法分析孔径图)
5. 总结
本文采用实验室的介孔氧化铝材料、微孔炭材料、沸石分子筛以及微介孔的炭材料,结合BJH理论、HK理论、SF理论以及NLDFT理论模型的原理,分析总结了各种理论模型的使用条件,为多孔材料孔径分析模型的选择提供了选择依据,有利于减小孔径分析误差。
1) 多孔材料在进行孔径分析时,要选择合适的理论模型,才能够得出准确的结果。
2) 介孔材料,如果是圆柱型孔或者接近圆柱型孔的,可以选择BJH理论进行孔径分析,若是孔径大于5 nm的介孔材料,孔径分析的结果更准确。
3) HK理论模型适用于狭缝孔的微孔炭材料孔径分析,分析结果比较准确;SF法更适用于圆柱型的微孔分子筛材料,需要基于微孔材料氩气吸附的等温线进行孔径分析。
4) 对于微介孔材料,选择NLDFT理论分析结果是最准确的。NLDFT理论可以用于全孔分析,在选择Kenel文件时,要尽量保证孔型与材料相符,保证模拟吸附等温线与实验吸附等温线误差最小,才能提高分析结果的准确性。
文章引用
暴丽霞,高培峰,彭绍春. 多孔材料孔径分布测试方法的研究
Analysis Method of Pore Size Distribution of Porous Materials[J]. 材料科学, 2020, 10(02): 95-103. https://doi.org/10.12677/MS.2020.102012
参考文献
- 1. Ying, J.Y., Mehner, C.P. and Wong, M.S. (1999) Synthesis and Applications of Supramolecular-Templated Mesoporous Materials. Angewandte Chemie International Edition, 38, 56 -77.
- 2. 闫继娜, 施剑林, 陈航榕, 等. 纳米介孔材料的催化应用前景[J]. 无机材料学报, 2003, 18(4): 725-730.
- 3. 侯梅芳, 崔杏雨, 李瑞丰. 沸石分子筛在气体吸附分离方面的应用研究[J]. 太原理工大学学报, 2001, 32(2): 135-139 .
- 4. Yu, J.C., Wang, X. and Fu, X. (2004) Pore-Wall Chemistry and Photocatalytic Activity of Mesoporous Titania Molecular Sieve Films. Chemistry of Materials, 16, 1523-1530. https://doi.org/10.1021/cm049955x
- 5. 刘欣梅, 阎子峰, Lu, G.Q. 介孔纳米二氧化锆的微观结构及其应用[J]. 科学通报, 2004, 49(6): 522-527.
- 6. Hou, K., Tian, B., Li, F., et al. (2005) Highly Crystallized Mesoporous TiO2 Films and Their Applications in Dye Sensitized Solar Cells. Journal of Materials Chemistry, 15, 2414 -2420. https://doi.org/10.1039/b417465h
- 7. Choi, S.Y., Mamak, M., Coombs, N., Ozin, G.A., et al. (2004) Electrochromic Performance of Viologen-Modified Periodic Mesoporous Nanocrystallineanatase Electrodes. Nano Letters, 4, 1231 -1235. https://doi.org/10.1021/nl049484d
- 8. Ye, B., Trudeau, M. and Antonelli, D. (2001) Synthesis and Electronic Properties of Potassium Fulleride Nanowires in a Mesoporous Niobium Oxide Host. Advanced Materials, 13, 29-33. https://doi.org/10.1002/1521-4095(200101)13:1<29::AID-ADMA29>3.0.CO;2-A
- 9. Skadtchenko, B.O., Trudeau, M., Kwon, C.W., et al. (2004) Antonelli, Synthesis and Electrochemistry of Li-and Na-Fulleride Doped Mesoporous Taoxides. Chemistry of Materials, 16, 2886-2884. https://doi.org/10.1021/cm030548f
- 10. Zhe, L.Z. and Zheng, H.Y. (2013) Theoretical and Practical Discussion of Measurement Accuracy for Physisorption with Micro-and Mesoporous Materials. Chinese Journal of Catalysis, 34, 1797-1810. https://doi.org/10.1016/S1872-2067(12)60601-9
- 11. Lowell, S. and Shields, J.E. (1991) Powder Surface Area and Porosity. 3rd Edition, Chapman and Hall, New York, 119. https://doi.org/10.1007/978-94-015-7955-1
- 12. 郭静, 张芬丽, 刘玉霞. 微介孔复合材料孔径分析方法对比[J]. 河南化工, 2017, 34(9): 52-55.
- 13. Cai, G.H., Zheng, X.H., Zheng, Y., Xiao, Y. and Zheng, Y. (2016) Synthesis of Ordered Mesoporous Boron-Doped γ-Alumina with High Surface Area and Large Pore Volume. Materials Letters, 178, 248-251.https://doi.org/10.1016/j.matlet.2016.04.041
- 14. Groen, J.C., Peffer, L.A.A. and Perez-Ramirez, J. (2003) Pore Size Determination in Modified Micro- and Mensoporous Materials. Pitfalls and Limitations in Gas Adsorption Data Analysis. Microporous and Mesoporous Materials, 60, 1-17. https://doi.org/10.1016/S1387-1811(03)00339-1
- 15. Lowell, S., Shields, J.E., Thomas, M.A.J. and Thommes, M. (2003) Characterization of Porous Solids and Powders: Surface Area, Pore Size and Density. Kluwer Academic Publishers, Dordrecht. https://doi.org/10.1007/978-1-4020-2303-3
- 16. 辛勤, 罗盂飞. 现代催化研究方法[M]. 北京: 科学出版社, 2009.
- 17. Horvath, G. and Kawazoe, K. (1983) Method for the Calculation of Effective Pore Size Distribution in Molecular Sieve Carbon. Journal of Chemical Engineering of Japan, 16, 470. https://doi.org/10.1252/jcej.16.470
- 18. Gelb, L.D., Gubbins, K.E., Radhakrishnan, R., et al. (1999) Phase Separation in Confined Systems. Reports on Progress in Physics, 62, 1573. https://doi.org/10.1088/0034-4885/62/12/201
- 19. Thommes, M. and Findenegg, G.H. (1994) Pore Condensation and Critical-Point Shift of a Fluid in Controlled-Pore Glass. Langmuir, 10, 4270-4277. https://doi.org/10.1021/la00023a058
- 20. Thommes, M., Koehn, R. and Froeba, M. (2002) Sorption and Pore Condensation Behavior of Pure Fluids in Mesoporous MCM-48 Silica, MCM-41 Silica, SBA-15 Silica and Controlled-Pore Glass at Temperatures Above and Below The Bulk Triple Point. Applied Surface Science, 196, 239-249. https://doi.org/10.1016/S0169-4332(02)00062-4
- 21. Thommes, M., Köhn, R. and Fröba, M. (2000) Sorption and Pore Condensation Behavior of Nitrogen, Argon, and Krypton in Mesoporous MCM-48 Silica Materials. The Journal of Physical Chemistry B, 104, 7932-7943. https://doi.org/10.1021/jp994133m
- 22. Walton, J.P.R.B. and Quirke, N. (1989) Capillary Condensation: A Molecular Simulation Study. Molecular Simulation, 2, 361-391. https://doi.org/10.1080/08927028908034611