Computer Science and Application
Vol.4 No.10(2014), Article ID:14247,7 pages
DOI:10.12677/CSA.2014.410033
CT Image Reconstruction Algorithm Based on Anisotropic Total Variation Minimization
College of Computer Science, Beijing University of Technology, Beijing
Email: 983956323@qq.com
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Sep. 4th, 2014; revised: Oct. 4th, 2014; accepted: Oct. 15th, 2014
ABSTRACT
In many practical applications, due to the data acquisition time, dose, and geometric constraint scanning, only in a limited Angle range, various data is available to acquire. It is the so-called few-view problem. In recent years, the Total Variation (TV) minimization model, using alternating direction method (ADM) in sparse optimization algorithm shows better reconstruction results among these TV-based algorithms. However, Isotropic TV minimization based algorithms for fewview reconstruction has not so good accuracy and there is further improvement to achieve. Aiming at this problem, Anisotropic TV minimization algorithm is proposed in this paper. The algorithm is based on ADM and uses sparse optimization theory. Experimental results demonstrate that the proposed method compared with Isotropic TV minimization algorithm, has higher reconstruction accuracy and a more excellent comprehensive performance.
Keywords:CT Image Reconstruction, Few-View Reconstruction, Total Variation Minimization, Alternating Direction Method, Anisotropic Total Variation Minimization

一种基于各向异性总变分最小化的
CT图像重建算法
张 莹,王 丹
北京工业大学计算机学院,北京
Email: 983956323@qq.com
收稿日期:2014年9月4日;修回日期:2014年10月4日;录用日期:2014年10月15日

摘 要
由于受数据采集时间、照射剂量、成像系统扫描的几何位置等因素的约束,计算机断层成像(CT)技术目前只能在有限角度范围或在较少的投影角度得到数据,这些都属于不完全角度重建问题。图像重建问题中的总变分(Total-Variation, TV)最小化模型使用基于交替方向法(alternating direction method, ADM)的稀疏优化算法能够在不完全角度的图像重建中获得较优的重建结果。然而,在极稀疏的角度数量下,各向同性TV最小化算法的重建精度不是很理想,存在进一步改善空间。本文针对该问题,通过基于稀疏优化的交替方向方法推导基于各向异性TV最小化的CT图像重建算法。实验结果表明,在稀疏角度重建中,本文提出的基于各向异性TV最小化重建算法与各向同性TV最小化重建算法相比,在稀疏性保持良好的基础上,重建精度上存在优势,综合性能方面表现更优异。
关键词
计算机断层成像,不完全角度重建,总变分最小化,交替方向法,各向异性总变分最小化

1. 引言
计算机断层成像(CT)技术是一种利用图像重建算法计算得到物体的内部信息的透视成像技术。由于所采用的解析算法对数据完整性有较高要求,在不完全角度重建问题中,解析算法得到的重建结果不是很理想。所以,通常会考虑对数据完整性要求较低的迭代算法。但是迭代算法在占用存储空间和运算时间方面远不如解析算法。另外,对于缺失投影角度较多的不完全角度问题,传统迭代算法如ART算法[1] 等,得到的重建结果也不令人满意。
近年来,压缩感知(Compressive Sensing, CS)理论[2] -[4] 的提出及发展极大地促进了CT图像重建算法的进步。CS理论利用信号、信息的稀疏性,使信号采集能力、信息处理能力极大提升。2006年,提出CS理论的Candes等人[2] 首次提出了将带有约束的总变分(Total-Variation, TV)最小化模型应用于图像重建的想法,并得到了效果非凡的重建结果。
将基于交替方向法的稀疏优化算法应用于TV最小化模型能够得到较优的求解结果。其中最经典的两类方法分别是Split Bregman(SB)方法[5] 和基于增广Lagrangian函数的ADM算法[6] 。2011年,Vandeghinste等人[7] 在CT图像重建中运用了SB方法,并得到了比ASD-POCS(Adaptive Steepest Descent-Projection Onto Convex Sets)算法更好的重建效果。另外,在对收敛性验证方面,2012年Deng和Yin [8] 对一般的ADM方法证明了全局收敛性及线性收敛速度。2013年Chen和Xu [9] 对应用于CT图像重建的线性SB方法证明了其收敛性。
在重建精度、收敛性能等方面,基于ADM的求解方法存在明显优势,使用优化理论的求解技巧对其求解过程进行改进后,算法性能、收敛度可进一步得到提高,然而在保证图像稀疏性良好的情况下,当投影角度数量更少时,各向同性TV最小化的重建效果还不太理想,需要进一步完善。本文针对该问题,提出了一种基于各向异性TV最小化的重建算法。通过仿真实验验证了该算法的性能,并通过对比实验证明了基于各向异性TV最小化重建算法与基于各向同性TV最小化重建算法相比,在收敛精度,综合性能方面表现更理想。
2. 基于各向异性TV最小化算法的设计与实现
2.1. 压缩感知理论下的图像稀疏表示
2006年Donoho[3] ,Candes和Tao[2] [4] 共同提出了CS理论,近年来在压缩图像、医学图像、数模转换、雷达成像、天文学、通信等领域都得到应用[10] 。相对于传统的从频域中获取数据重构图像的方法,CS理论有着不同的性质,即只需要通过少量的样本点就能够精确地重构原来的图像[11] 。
CS理论的基本结论为:对一个稀疏的离散信号,只需知道这个信号的部分频域取值,就能以高概率精确恢复这一信号。具体的恢复方式是通过求解一个凸规划实现的,该规划的目标函数为此信号的l1范数最小,约束条件由已知的频域取值得到。具体形式表示为如(1)所示。
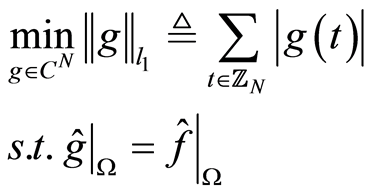 (1)
(1)
其中g为待恢复的N维实信号, 为约束条件,
为约束条件,![]() 为测量得到的g的频率采样值。
为测量得到的g的频率采样值。
然而,通常情况下,对于实际的图像函数,往往并不是稀疏的,这就需要通过稀疏变换的方式使其在变换域稀疏,进而利用CS理论求解。对于图像的稀疏变换,最常用的是离散余弦变换(discrete cosine transform, DCT)和离散小波变换(discrete wavelet transform, DWT),人们熟知的JPEG和JPEG2000图像压缩格式就分别利用了这两种变换。除此之外,在图像处理领域,还有一种非常知名的变换,广泛应用于多种模型之中,这就是离散梯度变换或差分变换,该变换的使用通常以总变分(Total-Variation, TV)最小化的形式出现。在使用TV时,又可以分为各向同性TV和各向异性TV,都通过离散梯度变换产生,定义如下如(2)所示。
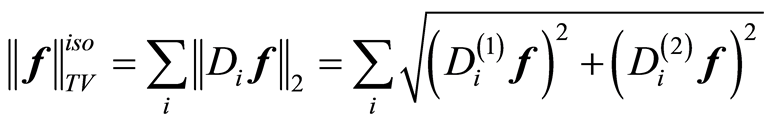 (2)
(2)
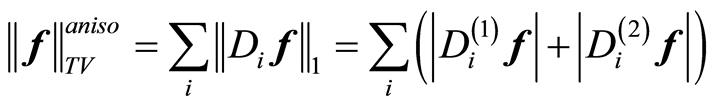 (3)
(3)
其中 表示对图像的第
表示对图像的第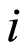 个像素进行水平和竖直方向差分的差分算子矩阵,对应的就是在第
个像素进行水平和竖直方向差分的差分算子矩阵,对应的就是在第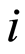 个像素上的离散梯度变换。不难看出两种TV的定义方式,所获得的稀疏性是相同的。
个像素上的离散梯度变换。不难看出两种TV的定义方式,所获得的稀疏性是相同的。
图1展示了对同一副图像,各种稀疏变换所得图像的稀疏性。其中图1(a)是256 × 256的Shepp-Logan体模,图1(b)是DCT变换后,将变换系数的绝对值大于最大值1%的点置1;其余置0的结果;图1(c)是DWT变换后的结果,图1(d)是离散梯度变换后将非0元素置1的结果。从图中可以明显的看出,对于该图像的离散梯度变换能够获得非常良好的稀疏性。与此同时,CS理论的研究成果也表明TV最小化模型能够在图像重建中取得较好的效果。而各向异性TV虽然在稀疏性上与各向同性TV相同,但在对图像的适应能力及优化的综合性能方面较各向同性TV仍存在优势。因此,本文主要对各向异性TV最小化重建算法进行研究,并比较其与各向同性TV算法的重建性能差异。
2.2. 基于各向异性TV最小化算法的设计与实现
大多数迭代型重建算法通常采用线性方程组来描述成像问题,对成像模型离散化之后得到如(4)所示的模型。
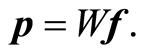 (4)
(4)




Figure 1. Schematic diagram of sparse transformed
图1. 稀疏变换后稀疏性示意图
其中![]() 表示被重建物体,
表示被重建物体,![]() 表示投影向量,
表示投影向量,![]() 表示投影系统矩阵。
表示投影系统矩阵。
对上述问题加入TV最小化的目标,得到公式(5):
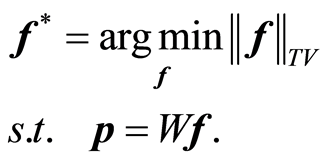 (5)
(5)
使用各向异性TV的定义方式: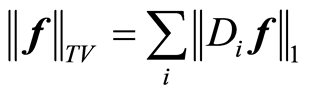 。其中,
。其中,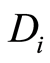 表示沿方向
表示沿方向![]() 的差分算子矩阵。
的差分算子矩阵。
对(5)式使用变量代换进行变形,得到公式(6):
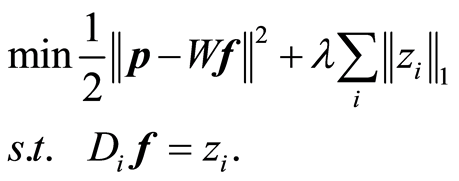 (6)
(6)
最小化其对应的增广Lagrangian函数,得到公式(7):
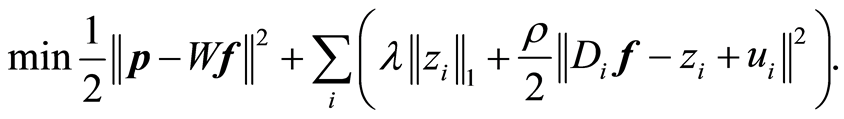 (7)
(7)
使用ADM,该问题的求解转化为“f-子问题”和“z-子问题”交替求解,得到公式(8):
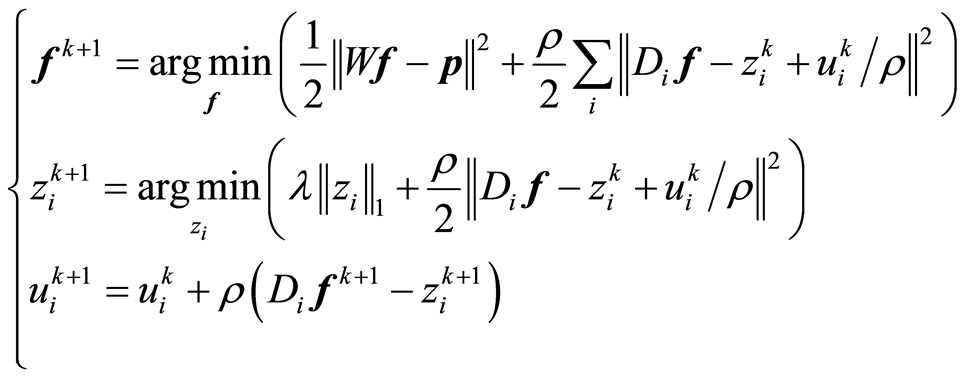 (8)
(8)
算法最终形式为公式(9)所示。
 (9)
(9)
其中![]() 表示矩阵
表示矩阵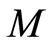 的Moore-Penrose伪逆。
的Moore-Penrose伪逆。
3. 实验结果
3.1. 稀疏性及采样条件分析
本文采用仿真数据对算法性能进行研究,重建对象为256 × 256的Shepp-Logan体模,在稀疏角度重建实验中,需要对精确重建所需的投影角度数量进行估计,首先要对图像的稀疏性进行估计。
稀疏重建实验中扫描与重建基本参数在表1中列出,其中不包含投影角度数量,我们需要对其数量变化所带来的性能影响进行研究。对于待重建体模,其稀疏性为2184,利用CS理论中精确重建必要条件对方程数量的要求,角度数量的下界应为(2184 × 2 + 1)/512 = 8.533,因此本文重建实验角度选择从10开始递增。
3.2. 仿真数据重建
对本文提出算法进行锥束圆轨迹不完全角度采集的仿真实验进行验证,采集角度选择360度范围内均匀分布的10个角度,同时使用各向同性TV最小化算法进行对比。两种算法迭代1000轮的重建结果在图2中展示。从图2中可以看出,两种算法的重建结果都未能达到理想的重建质量。两种算法重建结果的均方根误差(root mean squared error, RMSE)在表2中列出,从表2可以看出,各向异性TV最小化算法在重建精度上优于各向同性算法。
表1. 仿真实验扫描与重建参数
 (a)
(a) (b)
(b)
Figure 2. 10 angle reconstruction results (a) the results of the isotropic TV reconstruction algorithm; (b) the results of the anisotropic TV reconstruction algorithm
图2. 10角度重建结果 (a) 各向同性TV算法重建结果;(b) 各向异性TV算法重建结果
表2. 不同角度下重建结果均方根误差比较
而后采集角度选择360度范围内均匀分布的12个角度,两种算法迭代1000轮的重建结果在图3中展示。从图3中可以看出,本文提出的各向异性TV最小化算法在重建质量上优于各向同性算法。图4展示两种算法14个角度下的重建结果,仍然可以看出各向异性算法重建质量具有优势。两种算法重建结果的均方根误差也在表2中列出,可以看出各向异性算法已经达到了较高的重建精度。
最后采集角度选择360度范围内均匀分布的16和18个角度,在图5中展示16角度下两种算法迭代1000轮的重建结果。从图5中可以看出,两种算法都达到了非常理想的重建质量。两种算法重建结果的均方根误差也在表2中列出,可以看出两种算法均已达到较高的重建精度。
通过表2对两种算法的重建精度进行整体比较,不难发现,各向异性TV最小化算法在各个角度下整体精度优于各向同性算法。特别是12角度和14角度的重建结果表明,各向异性算法能够在更少的角度数量下达到理想的重建精度。文献[12] 对有限角度情况下各向异性与各向同性算法的性能差异进行了研究,也表明各向异性算法更有优势。
以上所有实验中算法全部于Matlab2013b环境下运行,运行平台为AMAX Tesla工作站:Intel Xeon E5520 CPU 2.27 GHz和24 GB内存。由于算法表达形式相似,运行时间方面几乎不存在差异。
4. 结论
本文针对稀疏角度重建问题,提出了一种各向异性TV最小化重建算法,该算法利用ADM推导迭代
 (a)
(a) (b)
(b)
Figure 3. 12 angle reconstruction results (a) the results of the isotropic TV reconstruction algorithm; (b) the results of the anisotropic TV reconstruction algorithm
图3. 12角度重建结果 (a) 各向同性TV算法重建结果;(b) 各向异性TV算法重建结果
 (a)
(a) (b)
(b)
Figure 4. 14 angle reconstruction results (a) the results of the isotropic TV reconstruction algorithm; (b) the results of the anisotropic TV reconstruction algorithm
图4. 14角度重建结果 (a) 各向同性TV算法重建结果;(b) 各向异性TV算法重建结果
 (a)
(a) (b)
(b)
Figure 5. 16 angle reconstruction results (a) the results of the isotropic TV reconstruction algorithm; (b) the results of the anisotropic TV reconstruction algorithm
图5. 16角度重建结果 (a) 各向同性TV算法重建结果;(b) 各向异性TV算法重建结果
算法框架,子问题求解简单易行,能够获得较好的收敛性质和重建效果。在极稀疏的角度数量下,本文利用仿真实验验证了所提出的算法性能,并与各向同性TV算法进行了对比。实验结果表明,本文提出算法能够在稀疏角度重建中使用极少的投影角度获得优异的重建效果。此外,对比实验结果也表明各向异性TV最小化算法在重建精度上确实比各向同性算法存在优势,特别是获得较高重建质量所需的投影角度数量更少。这些都将成为算法在实际数据的稀疏角度重建中充分发挥效能的潜在优势。
参考文献 (References)
- [1] Andersen, A.H. (1989) Algebraic reconstruction in CT from limited views. IEEE Transactions on Medical Imaging, 8, 50-55.
- [2] Candes, E., Romberg, J. and Tao, T. (2006) Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency Information. IEEE Transactions on Information Theory, 52, 489-509.
- [3] Donoho, D. (2006) Compressed sensing. IEEE Transactions on Information Theory, 52, 1289-1306.
- [4] Candes, E. and Tao, T. (2005) Decoding by linear programming. IEEE Transactions on Information Theory, 59, 1207-1223.
- [5] Goldstein, T. and Osher, S. (2009) The split Bregman method for l1 regularized problems. SIAM Journal on Imaging Sciences, 2, 323-343.
- [6] Li, C. (2009) An efficient algorithm for total variation regularization with applications to the single pixel camera and compressive sensing. Rice University, Houston.
- [7] Vandeghinste, B., Goossens, B., Beenhouwer, J., et al. (2011) Split-Bregman-based sparse-view CT reconstruction. 11th International Meeting on Fully Three-Dimensional Reconstruction in Radiology and Nuclear Medicine, 431-434.
- [8] Deng, W. and Yin, W. (2012) On the global and linear convergence of the generalized alternating direction method of multipliers. Rice CAAM Report, 12-14.
- [9] Chen, C. and Xu, G. (2013) The linearized split Bregman iterative algorithm and its convergence analysis for robust tomographic image reconstruction. UCLA CAM Report, 13-66.
- [10] 喻玲娟, 谢晓春 (2008) 压缩感知理论简介. 数字视频, 12, 16-18.
- [11] 傅迎华 (2008) 可压缩传感重构算法与近似QR分解. 计算机应用, 9, 2300-2302.
- [12] Chen, Z., Jin, X., Li, L., et al. (2013) A limited-angle CT reconstruction method based on anisotropic TV minimization. Physics in Medicine and Biology, 58, 2119-2141.
