Computer Science and Application
Vol.06 No.08(2016), Article ID:18315,5
pages
10.12677/CSA.2016.68058
A Composite Velocity Measurement Method Based on Chirp-Step
Chen Wang, Yun Fu, Xuting Zhou
School of Physics and Electronic Information, Anhui Normal University, Wuhu Anhui

Received: Jul. 24th, 2016; accepted: Aug. 11th, 2016; published: Aug. 17th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Millimeter wave (MMW) Chirp-Step Costas coded radar is a high-resolution distance radar, and motion compensation has to be implemented to improve resolution of moving target. This paper adopts an approach for motion compensation based on Pulse-Doppler velocity, and analyzes the effect of compensation for high velocity target with diversified velocity. The simulation result confirms effective and fast effect of the technology. High resolution 1-D range profile is generated by using the algorithm.
Keywords:MMW Radar, Composite Speed, Chirp-Step, Costas Code, Pulse-Doppler

一种基于Chirp-Step的复合测速方法
王宸,傅赟,周旭廷
安徽师范大学物理与电子信息学院,安徽 芜湖

收稿日期:2016年7月24日;录用日期:2016年8月11日;发布日期:2016年8月17日

摘 要
毫米波Costas调频步进(Chirp-Step)编码雷达是一种距离高分辨率雷达,实现运动目标的距离高分辨必须进行运动补偿。本文采用脉冲多普勒测速的运动补偿方法,并对其在不同速度下,对高速运动目标的补偿进行了仿真分析。结果表明该方法补偿精度高,运算速度快。用该方法速度补偿后,可以得到运动目标的高分辨一维距离像。
关键词 :毫米波雷达,复合测速,调频步进,Costas编码,脉冲多普勒

1. 引言
提高距离分辨率是现代雷达应用的一个重要研究方向。由于雷达的距离分辨率与信号带宽成反比,所以为获得高分辨率的距离像必须采用大带宽信号。频率步进信号通过发射一串频率跳变的脉冲信号,能够在降低信号处理瞬时带宽的条件下实现距离高分辨,因而近年来得到了较深入的研究 [1] ,但是对速度及其敏感,容易产生速度模糊,不利于对目标的测速、测距,为了提高分辨率,文献 [2] 提出了正负调频测速法,该方法要求目标合成距离像不能存在距离模糊,对系统参数要求较高;文献 [3] 提出波形熵法获得一维距离像,但是当脉冲个数较少且脉冲重复频率较大时,离像峰值的发散和衰减很不明显,补偿后每幅距离像的波形熵相差不大,不能清晰地出现全局最小值,此时最小波形熵法不再适用。与前述相比,Costas频率编码信号 [2] 具有近似理想的“图钉”形模糊函数,消除了距离-多普勒耦合,但由于目标运动产生的多普勒失配引起能量发散,为了使聚焦理想,必须进行运动补偿。
因此,一种新的方法,基于脉冲多普勒测速的方法被提出 [4] [5] ,这种方法首先用相邻的两帧脉冲信号实现脉冲多普勒测速,用已知速度对目标一维距离像补偿,由于回波没用峰值走动,只是能量发散,所以补偿后可以使目标能量集中,从而生成高分辨一维距离像。该方法计算量减小,易于实现。本文首先分析了毫米波Costas编码雷达的原理和多普勒性能,在此基础上采用脉冲多普勒测速的方法进行运动补偿,并给出仿真结果。
2. 目标运动对Costas编码雷达的影响
2.1. 信号形式及基本处理
毫米波Costas编码雷达的发射信号是一帧载频Costas编码的相参脉冲序列,设调频步进信号的脉冲个数为N,脉冲宽度为TP,脉冲重复周期为Tr,频率进步量为Δf,第一个子脉冲的中心载频为f0,则雷达发射的脉冲序列的数学表达式为 [6] - [8] :
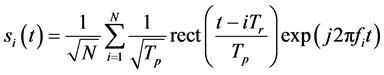 (1)
(1)
式中: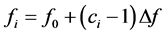 ,ci为Costas序列。
,ci为Costas序列。
对于距离为Rm的目标,假设有有M个散射点,用与发射脉冲信号载频相同的相参本振进行混频,经过I/Q正交及归一化处理,可得目标回波的复包络输出为 [9] - [11] :
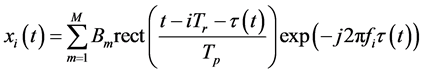 (2)
(2)
式中: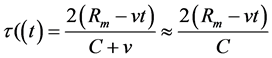 为目标回波时延;这里Rm是第m个散射点到雷达的初始距离,
为目标回波时延;这里Rm是第m个散射点到雷达的初始距离,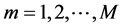 ;v为目标的径向速度;C为光速;Bm为第m个散射点回波的幅值。
;v为目标的径向速度;C为光速;Bm为第m个散射点回波的幅值。
把 代入式(2),取样得:
代入式(2),取样得:
 (3)
(3)
其中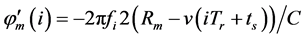 ,这里ts是采样时间,
,这里ts是采样时间,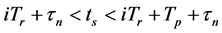 ,τn是第n个散射中心到雷达的时延。上述数学表达式可以作类似的理解:一组等间隔的频率谱线,经过Costas编码后,向线性目标系统发射,对目标进行激励,其回波是对目标系统的频域采样,对得到的频域信息调序后进行IFFT,就可以得到相应的时域信息。即目标一维距离像,当目标有速度时,发生多普勒频移,则目标系统为一个非线性系统, 必须进行补偿后才能处理。当步进频率信号经过Costas编码调制时,信号的顺序被打乱,必须将xi(ts)按频率步进方式整序才能进行IFFT。
,τn是第n个散射中心到雷达的时延。上述数学表达式可以作类似的理解:一组等间隔的频率谱线,经过Costas编码后,向线性目标系统发射,对目标进行激励,其回波是对目标系统的频域采样,对得到的频域信息调序后进行IFFT,就可以得到相应的时域信息。即目标一维距离像,当目标有速度时,发生多普勒频移,则目标系统为一个非线性系统, 必须进行补偿后才能处理。当步进频率信号经过Costas编码调制时,信号的顺序被打乱,必须将xi(ts)按频率步进方式整序才能进行IFFT。
2.2. 多普勒效应
Costas编码消除了距离–多普勒耦合,消除了目标一维距离像的峰值走动,但是经过编码之后,相当于在各步进信号之间引入了随机变量,所以引起目标一维距离像能量发散,为了使聚焦理想,必须进行运动补偿。
对于以速度v运动的目标,令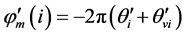 ,这里,
,这里,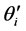 和
和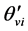 分别是与速度无关的项和与速度有关的项,它们表示为:
分别是与速度无关的项和与速度有关的项,它们表示为:
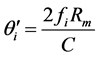 (4)
(4)
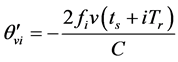 (5)
(5)
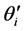 是静止时的正常相位关系,
是静止时的正常相位关系,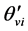 是速度引起的相移。
是速度引起的相移。
3. 基于多普勒测速的运动补偿
3.1. 多普勒测速方法
相邻的两帧Costas编码脉冲回波,第一帧和第二帧之间相同载频的脉冲相差时间为NTr。则第一帧的信号回波如式(3)所示,对第二帧脉冲回波,在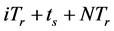 时刻采样,可得到:
时刻采样,可得到:
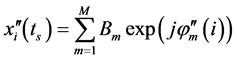 (6)
(6)
式中,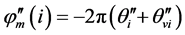 ,
, ,
, 。
。
Costas编码雷达不存在距离–多普勒耦合造成的峰值走动,所以每一个散射中心不会移动到别的距离单元。由式(3)和式(6),我们可得到如下表达式:
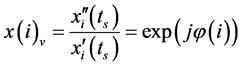 (7)
(7)
式中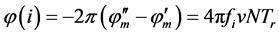 ,所以
,所以
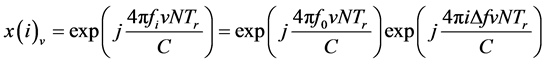 (8)
(8)
对式(8)作FFT,可得
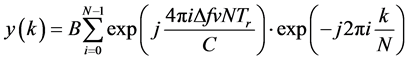 (9)
(9)
式中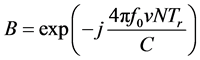 ,所以
,所以
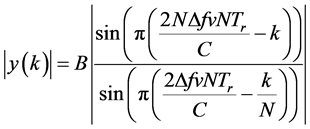 (10)
(10)
当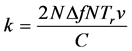 时,
时,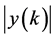 有最大值,所以目标速度为:
有最大值,所以目标速度为:
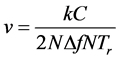 (11)
(11)
由式(11)得到的速度对式(3)作速度补偿,然后在作FFT,可得到高分辨的一维距离像。
3.2. 仿真
为考察脉冲多普勒测速法速度补偿的性能,本文用如下参数进行仿真:目标有2个强散射点,Rm = [340 m 344 m 350],f0 = 94 GHz,Δf = 10 MHz,Tr = 40 us,Tp = 100 ns, N = 64。仿真速度设置为[−110 m/s, 110 m/s]。
从以上图中可以看出,对于Costas编码步进频信号,运动目标回波本身不存在峰值走动,但是能量发散严重,当速度大于2.5 m/s时,峰值较小的散射点几乎淹没,用脉冲多普勒测速法速度补偿是对目标回波进行聚焦。图1分别是速度为0、2.5 m/s、v = 110 m/s时,目标的一维距离像,由图1看出,在速度为10 m/s时,由于能量发散,目标一维距离像已经完全找不到目标的位置,图2是经过速度补偿后的一维距离像,它们补偿前的速度分别是2.5 m/s、50 m/s和110 m/s。补偿后,能量被集中,从而生成目标的高分辨一维距离像,可以进行精确的测距、目标识别等处理。由于Costas编码信号的回波没用峰值走动,只需要使用本方法集中信号的能量,即使有测速误差,只要能量的集中能找到峰值点,就能正确测出举例。因此用脉冲多普勒测速方法进行速度补偿,适合Costas编码雷达的运动补偿处理。


 (a) (b) (c)
(a) (b) (c)
Figure 1. Range image of target before speed compensation. (a) v = 0 m/s; (b) v = 2.5 m/s; (c) v = 110 m/s
图1. 速度补偿前目标一维距离像。(a) v = 0 m/s; (b) v = 2.5 m/s; (c) v = 110 m/s


 (a) (b) (c)
(a) (b) (c)
Figure 2. Range image of the target after speed compensation. (a) v = 2.5 m/s; (b) v = 10 m/s; (c) v = 110 m/s
图2. 速度补偿后目标一维距离像。(a) v = 2.5 m/s; (b) v = 10 m/s; (c) v = 110 m/s
4. 结束语
本文运用脉冲多普勒测速的运动补偿方法对毫米波Costas编码动目标一维距离像进行运动补偿,仿真结果表明该方速度快、补偿效果好,经过补偿后的目标一维距离像,可以进行精确的测距及目标识别。
文章引用
王宸,傅赟,周旭廷. 一种基于Chirp-Step的复合测速方法
A Composite Velocity Measurement Method Based on Chirp-Step[J]. 计算机科学与应用, 2016, 06(08): 472-476. http://dx.doi.org/10.12677/CSA.2016.68058
参考文献 (References)
- 1. 孙慧霞, 刘峥. 毫米波调频步进雷达复合测速方法[J]. 系统工程与电子技术, 2011, 33(3): 539-543.
- 2. 刘峥, 刘宏伟. 正负步进频率编码信号及其处理[J]. 信号处理, 1999(S1): 21-25.
- 3. 刘静, 李兴国, 吴文. 波形熵法在毫米波Costas跳频雷达运动补偿中的应用[J]. 红外与毫米波学报, 2003, 22(4): 303-306.
- 4. 刘静, 李兴国, 吴文. 毫米波Costas编码雷达动目标一维距离像运动补偿[J]. 红外与毫米波学报, 2005, 24(5): 344-347.
- 5. 魏玺章, 刘振, 邓斌, 黎湘. Costas编码跳频宽带雷达信号测速技术研究[J]. 电子学报, 2010, 38(10): 2426-2429.
- 6. 王桂丽, 李兴国. 频率步进和脉冲多普勒复合测速研究[J]. 红外与毫米波学报, 2008, 27(3): 190-192.
- 7. Orlenko, V.M. (2004) Simulation of Target Detection Using a High Range Resolution Radar. Ultraw Ultrash Impulse Signal, 9, 19-22. http://dx.doi.org/10.1109/uwbus.2004.1388068
- 8. De Maio, A., Farina, A. and Gerlach, K. (2007) Adaptive Detection of Range Spread Targets with Orthogonal Rejection. IEEE Transactions on Aerospace and Elec-tronic Systems, 43, 738-751. http://dx.doi.org/10.1109/TAES.2007.4285365
- 9. Jia, S.G. and Kong, L.J. (2009) A New Approach to Range Spread Target Detection Based on Information Entropy. 2009 2nd Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xi’an, 26-30 October 2009, 560-562. http://dx.doi.org/10.1109/APSAR.2009.5374222
- 10. Farina, A. and Studer, F.A. (1991) Detection with High Resolution Radar: Great Promise, Big Challenge. Microwave Journal, 24, 263-273.
- 11. 孙慧霞, 刘峥. 毫米波调频步进雷达复合测速方法[J]. 系统工程与电子技术, 2011, 33(3): 539-543.