Computer Science and Application
Vol.
08
No.
10
(
2018
), Article ID:
27193
,
8
pages
10.12677/CSA.2018.810164
Network Maximum Flow Analysis Base on Dinic’s Algorithm
Gang Li, Jinbao Miao, Chun’an Hu
Information Engineering, Jiangxi University of Science and Technology, Ganzhou Jiangxi

Received: Oct. 2nd, 2018; accepted: Oct. 15th, 2018; published: Oct. 22nd, 2018

ABSTRACT
This paper mainly analyzes the problem of calculating the maximum flow of the network by the Dinic algorithm. First we review the basic concepts of residual networks and hierarchical networks, then analyze the specific process of calculating the maximum flow of the network by the Dinic algorithm. By comparing with the Ford-Fulkerson algorithm and the Edmonds-Karp algorithm, the highlight of the Dinic algorithm is demonstrated. Through the comparison of correlations, the conclusion is that the Dinic algorithm works better than Ford-Fulkerson and is better than Edmonds-Karp.
Keywords:Dinic, Network Flow, Maximum Flow, Augmenting Chain
基于连续最短增广链的网络最大流分析
李港,苗金宝,胡春安
江西理工大学,信息工程学院,江西 赣州

收稿日期:2018年10月2日;录用日期:2018年10月15日;发布日期:2018年10月22日

摘 要
本文主要是分析连续最短增广链算法计算网络最大流的问题。先综述残留网络和层次网络的基本概念,然后分析连续最短增广链算法计算网络最大流的具体过程,再通过与Ford-Fulkerson (福特-富尔克森算法)和Edmonds-Karp (埃德蒙兹-卡普算法)算法进行比较来体现出连续最短增广链算法的突出点。通过相关性的比较,结论是连续最短增广链算法运行效果明显比Ford-Fulkerson好,且优于Edmonds-Karp。
关键词 :连续最短增广链,网络流,最大流,增广链

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
网络流中最大流问题是一个经典的问题,在最初的Ford-Fulkerson算法提出到现在已有60多年的历史了 [1] ,一直是个值得研究的问题。在此过程中,也提出了许多与之相关的算法。相比于初期的算法,现在对于网络最大流的算法得到了很大的改进,算法时间和空间复杂度都有所下降。常用的算法为Ford-Fulkerson算法 [2] 、Edmonds-Karp算法 [3] 和Dinic算法 [4] 等。
Ford-Fulkerson算法是利用深度优先搜索的思想来寻找增广链,而这样寻找会使得复杂度依赖于最大传输量。Edmonds-Karp算法则在Ford-Fulkerson算法的基础上进行了修改,使得每次按最短路径寻找增广链,但每次找完一个最短增广链后需要重新寻找,利用率不高。而Dinic算法则是效率更高,使用更频繁。
为此,本文对连续最短增广链算法在网络最大流问题上做一个详细的分析。该算法虽然也是按最短路径来寻找增广链的,不过增加了一个层次网络。相比于每次重新寻找最短增广链来说,利用层次网络将避免了重新寻找最短的增广链所带来的多余的步骤。
2. 基本概念
2.1. 基本定义
定义1.1:有向图为D = (V, E)。V为节点集合,E为边集合,D为由E和V构成的有向图。
定义1.2:对于任意一条边e =
定义1.3:f(e)为该边e现有的传输量,对于任意的边e Î E,它将有0 ≤ f(e) ≤ c(e)。
定义1.4:容量网络中会有一个源点s和一个汇点t。对于给定的容量网络,将存在源点s和汇点t,分别表示网络图中的起点和终点。其它为中间顶点,源点s需要通过中间顶点传输到汇点。
定义1.5:容量网络为G = (V, E, C)。见图1,对于任意边e,将有(c(e), f(e)),其中c(e)为最大容量,f(e)为实际传输量。

Figure 1. Capacity-network
图1. 容量网络
2.2. 预备知识
学会连续最短增广链算法首先需要了解的是残留容量网络。设有容量网络为G = (V, E, C),那么残留容量网络为G'(V', E', C') [5] ,其中G'的顶点集不变,即V' = V,但对于E'来说,就发生了改变。如果G中存在e =
了解残留网络还是不够的,还需要理解层次网络 [6] 。见图3,在层次网络中,源点s的层次为0,在残留网络中将存在一顶点v Î V',那么源点s到达v的最短路径长度就是v的层次。从源点s开始,以广度优先搜索的方法构建层次网络,使的能找到一条最短的增广链。如果无法构建层次网络,就说明网络最大流的求解已经得知。
3. 连续最短增广链算法
3.1. 算法思路
连续最短增广链算法是先建立层次网络,然后基于层次网络找到最短的增广链,以达到最优解,并且在层次网络上每使用一次增广链后还可以重复使用,直到最短的增广链不存在。如果找不到最短的增广链就利用剩下的残留容量网络继续构建层次网络,并重复这些步骤。当层次网络无法构建时,那么网络最大流问题也就结束了。
已知有一容量网络为G = (V, E, C),顶点数为n,最大容量为C,实际传输量为f,层次数l,源点为s,汇点为t。
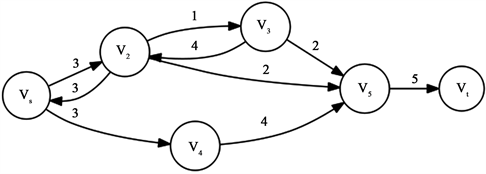
Figure 2. Residual network
图2. 残留网络

Figure 3. Hierarchical network
图3. 层次网络
步骤①:初始化容量网络G和可行流f,使的f = {0}。
步骤②:构建层次网络,设集合P为已经设置好层次的顶点集合,Q为已经从集合P中取出来使用的顶点集合,将源点s的层次设为0,即level(s) = 0,并将s加入集合P中,使的P = {s}。接着从P中取出一顶点v(v Î P,v ∉ Q),对于任意边e =
步骤③:利用层次网络寻找最短的增广链,而层次网络可以重复使用,并且寻找最短的增广链需要以源点s为出发点,以汇点t为终点。一开始以层次为0的点开始,即源点s,由于对于任意边e =
步骤④:若能构建层次网络,跳到步骤②,如若不能则网络最大流问题求解完毕。
3.2. 计算过程
下面将对一个具体的网络流进行分析,为了更好的理解连续最短增广链算法,模拟连续最短增广链算法计算网络最大流的过程。以图4为例进行分析。
图4中弧的数字表示最大容量,初始网络流值为0。设V1位源点,V6为汇点来计算网络图中的最大网络流。首先要构建层次网络,将源点V1的层次设为0,根据步骤②的思路来计算每个节点的层次数,得到的层次数如表1所示。
得到了层次网络后,就用它来寻找最短增广链。用层次网络能更快的查找出最短增广链,将得到两条最短增广链,分别是V1 → V2 → V3 → V6和V1 → V4 → V5 → V6。接着更新网络图,以便得到最新的残留网络。更新后的残留网络如图5所示,此时最大网络流为9。
图5中弧的两个数字分别为最大容量和实际传输量。在增广后明显可以看出V2 → V3这条边已经满了,无法再传输了,但根据增广链的思想,从V3 → V2还能传输6。现在增广后的网络图上再重新构建层次网络,构建后的层次数如表2所示。
INF表示无穷大,代表着无法从源点V1达到此点。此时可以得出最短增广链只有一条V1 → V2 → V4 → V5 → V6,继续在层次网络的基础上更新残留网络。得到的新的残留网络如图6所示。
由于此时不能再构建层次网络了,所以结束该算法,得到的网络最大流为11。连续最短增广链算法主要是利用构建好的层次网络能更快的查找最短增广链。
Table 1. The hierarchy number of the original network planning
表1. 原网络图中的层次数
Table 2. The hierarchy number of the original network planning after first update
表2. 第一次更新的残留网络中的层次数

Figure 4. The original network planning
图4. 原网络图
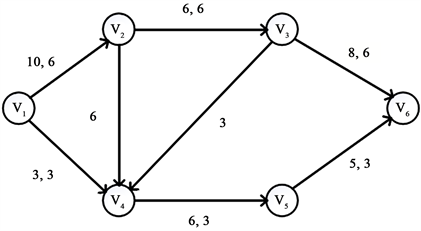
Figure 5. The residual network after first update
图5. 第一次更新的残留网络

Figure 6. The residual network after second update
图6. 第二次更新的残留网络
3.3. 算法复杂度分析
连续最短增广链算法需要重复运行步骤②和步骤③,构建层次网络以及查找最短增广链。已知容量网络G有V个顶点,E条边。在连续最短增广链算法中最多构建V分层次网络。
首先分析步骤②构建层次网络,层次网络是从源点开始,将每个节点与源点的距离算出来以确定节点的层次数。而这过程是用BFS思想 [7] 来实现的,这就需要遍历每一条边。即构建一个层次网络的时间复杂度是O(E),由于需要构建V个层次网络,所以构建层次网络总的时间复杂度是O(VE)。
步骤③是在层次网络的基础上寻找最短增广链。由于有E条边,那么最多将存在E条增广链。而对于每一条增广链,都是在层次网络的基础上寻找得来的。而层次数是与源点的距离,那么层次数最大是V,即最短增广链的长度最大为V。所以在寻找增广链上时间复杂度是O(VE)。由于最多构建V个层次网络,而在每个层次网络上寻找最短增广链的时间复杂度是O(VE),那么寻找增广链总的时间复杂度是O(EV2)。
综上所述,连续最短增广链的时间复杂度是O(EV + EV2),即O(EV2)。
4. 算法比较
1) Ford-Fulkerson算法,该算法是每次都寻找一条从源点s到汇点t的路径 [8] 。然后更新残留网络,直到找不到为止。由于该算法是每找到一条路径后更新残留网络,而残留网络每一条边的最大传输量是根据上一个残留网络得来。已知容量网络的最大传输量是F,那么该算法最坏情况下需要进行F次深度优先搜索,那么总的时间复杂度是O(FE),那么当F是很高时明显不是一种好方法。
2) Edmonds-Karp算法,该算法是每次寻找一条最短的增广链来进行更新 [9] 。由于每次查找一条最短的增广链就更新一次,而最坏情况下会有E条增广链。每次更新残留网络的话需要O(VE)的复杂度,那么总的时间复杂度是O(EV2),在存在增广链的条件下,E的最少数量是V − 1,当然实际情况是更多的,即E > V,对E进行平方明显不是最优的情况。
3) 连续最短增广链算法,该算法是分为V个阶段,每个阶段构建层次网络和查找最短增广链。先建立层次网络,在层次网络的基础上去找最短的增广链,而时间复杂度是O(EV2)。
一般情况下V < E,那么O(EV2)的时间复杂度优于O(EV2),而且不需要考虑最大容量上限的问题。不难看出,连续最短增广链算法运行效果明显比Ford-Fulkerson好,且优于Edmonds Karp。
5. 案例比较
例1:针对图7的图型模型,利用连续增广链算法求其最大流。
1) Ford-Fulkerson算法:在最佳情况下需要增广2次,最坏情况下需要增广4036次。该算法就是简单用DFS思想去寻找一条增广链,最坏情况下会一直是Vs → V2 → V5 → Vt和Vs → V4 → V5 → V2 → V3 → Vt这两条。这就需要增广4036次。当然如果正好寻找增广链是寻找到的是Vs → V2 → V3 → Vt和Vs → V4 → V5 → Vt这两条,就只需要增广2次,这是最好的情况。
2) Edmonds-Karp算法:在最佳情况下需要增广2次,最坏情况下需要增广3次。该算法相比Ford-Fulkerson算法,有一个优势,每次增广是按BFS思想寻找最短增广链的。所以在最坏情况下寻找到的增广链依次是Vs → V2 → V5 → Vt、Vs → V4 → V5 → Vt和Vs → V2 → V3 → Vt这三条。在最佳情况下的寻找到的增广链是Vs → V2 → V3 → Vt和Vs → V4 → V5 → Vt这两条。按最短路径寻找增广链相比于DFS毫无目的的寻找快的多。
3) Dinic算法:在最佳情况下需增广2次,最坏情况下需增广3次。该算法首先构建层次网络,在层次网络的基础上寻找最短增广链。最坏情况下寻找到的增广链分别Vs → V2 → V5 → Vt、Vs → V4 → V5 → Vt和Vs → V2 → V3 → Vt这三条。在最佳情况下寻找到的增广链是Vs → V2 → V3 → Vt和Vs → V4 → V5 → Vt这两条。相比于Edmonds-Karp算法每次寻找增广链都用BFS查找一遍来说,在层次网络的基础上寻找最短增广链将快的多。
例2:针对图8的图型模型,利用连续增广链算法求其最大流。
1) Ford-Fulkerson算法:在最佳情况下,需要增广2次,最坏情况需要增广4036次。用DFS来寻找增广链最坏情况下,增广链将会一直是Vs → V6 → V5 → Vt和Vs → V2 → V4 → V5 → V6 → Vt
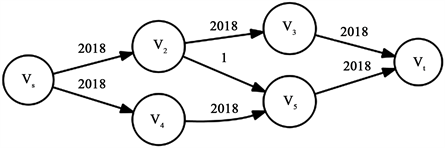
Figure 7. Example 1
图7. 案例1

Figure 8. Example 2
图8. 案例2
这两条。这就需要增广4036次。也有可能正好寻找到Vs → V6 → Vt和Vs → V2 → V4 → V5 → Vt这两条,这是最佳情况下,需要增广2次。
2) Edmonds-Karp算法:在最佳情况下需要增广3次,最坏情况下需要增广4次。按最短距离寻找增广链,最坏情况下将依次找到Vs → V6 → Vt、Vs → V2 → V3 → Vt、Vs → V2 → V6 → V5 → Vt和Vs → V2 → V4 → V5 → Vt这四条,最佳情况下将寻找到Vs → V6 → Vt、Vs → V2 → V3 → Vt和Vs → V2 → V4 → V5 → Vt这三条。
3) Dinic算法:在最佳情况需要增广3次,最坏情况下需增广4次。最坏情况下的增广链分别是Vs → V6 → Vt、Vs → V2 → V3 → Vt、Vs → V2 → V6 → V5 → Vt和Vs → V2 → V4 → V5 → Vt这四条。最佳情况下的增广链分别是Vs → V6 → Vt、Vs → V2 → V3 → Vt和Vs → V2 → V4 → V5 → Vt这三条。
整体来说连续最短增广链算法运行速度效果明显快于Ford-Fulkerson,而连续最短增广链算法是建立一个层次网络,使得查找最短的增广链可重复使用。又因为Edmonds-Karp算法每找到一个最短的增广链就更新下。所以可以得出结论:连续最短增广链算法效果明显比Ford-Fulkerson好,且优于Edmonds-Karp算法。
6. 结束语
网络最大流问题从提出来现在经历了这么多年,为了解决这个问题,提出了很多算法,算法复杂度也逐渐降低。为此,本文对主要常用的连续最短增广链算法,做了一个详细而全面的分析。由于连续最短增广链算法用到了一个层次网络,使得每次能快速地查找到最短的增广链并能重复使用。相比Edmonds-Karp算法有了明显时间上的优化,而且也不要像Ford-Fulkerson算法那样需要考虑容量网络中的最大传输量。
基金项目
江西理工大学创新基金资助项目(No.3103800226)。
文章引用
李 港,苗金宝,胡春安. 基于连续最短增广链的网络最大流分析
Network Maximum Flow Analysis Base on Dinic’s Algorithm[J]. 计算机科学与应用, 2018, 08(10): 1510-1517. https://doi.org/10.12677/CSA.2018.810164
参考文献
- 1. 张宪超, 陈国良, 万颖瑜. 网络最大流问题研究进展[J]. 计算机研究与发展, 2003, 40(9): 1281-1292.
- 2. Ford, L.R.J. and Fulkerson, D.R. (1954) Maximal Flow through a Network. Canadian Journal of Mathematics, 8, 399-404.
- 3. Edmonds, J. and Karp, R.M. (1972) Theoretical Improvements in Algorithmic Efficiency for Network Flow Problems. Journal of the ACM, 19, 248-264. https://doi.org/10.1145/321694.321699
- 4. Dinitz, E.A. (1970) Algorithm for Solution of a Problem of Maximum Flow in Networks with Power Estimation. Soviet Mathematics. Doklady, 1277-1280.
- 5. 谢政. 网络算法与复杂性理论[M]. 国防科技大学出版社, 2003.
- 6. 徐翠霞. 基于层次网络的最大流求解方法[J]. 潍坊学院学报, 2010, 10(4): 42-45.
- 7. Peleg, D. and Peleg, D. (2016) Sparse Fault-Tolerant BFS Structures. ACM.
- 8. Takahashi, T. (2016) The Simplest and Smallest Network on Which the Ford-Fulkerson Maximum Flow Procedure May Fail to Terminate. Technical Report of IeiceCst, 24, 390-394. https://doi.org/10.2197/ipsjjip.24.390
- 9. Lammich, P. and Sefidgar, S.R. (2016) Formalizing the Edmonds-Karp Algorithm. Interactive Theorem Proving. Springer International Publishing, 219-234.
