Computer Science and Application
Vol.
09
No.
05
(
2019
), Article ID:
30120
,
6
pages
10.12677/CSA.2019.95095
Research on the Improvement of Kernighan-Lin Algorithm for Graph Partitioning
Yong Yu, Shilin Kan, Na Zhao, Yongjun Luo, Jie Gu, Chenming Song
Key Laboratory in Software Engineering of Yunnan Province, School of Software, Yunnan University, Kunming Yunnan
Received: Apr. 24th, 2019; accepted: May 2nd, 2019; published: May 9th, 2019

ABSTRACT
With the development of Internet technology and the advent of the era of big data, the community division of complex networks has become a research hotspot. Among them, the large graph iterative calculation is the focus of its research, and the reduction of the communication edge between sub-graphs is to improve the computing capability. Kernighan-Lin algorithm is one of the simplest and most well-known heuristic algorithms in graph partitioning problem. Because traditional Kernighan-Lin algorithm is difficult to improve its execution efficiency in graph partitioning problem, this paper is based on the idea and graph of traditional algorithm. After the research of partitioning problem, an improved algorithm for Kernighan-Lin algorithm is proposed. Finally, using the karate club dataset as experimental data, the experimental results demonstrate the effectiveness and feasibility of the improved algorithm.
Keywords:Kernighan-Lin Algorithm, Graph Partitioning, Social Network
Kernighan-Lin算法的改进对图 划分问题的研究
郁湧,阚世林,赵娜,骆永军,顾捷,宋晨明
云南大学软件学院,云南省软件工程重点实验室,云南 昆明
收稿日期:2019年4月24日;录用日期:2019年5月2日;发布日期:2019年5月9日

摘 要
随着互联网技术的发展以及大数据时代的来临,复杂网络的社团划分已成为研究的热点,其中大图迭代计算作为其研究的重点,降低划分后子图之间的通信边规模是改善计算性能的关键。Kernighan-Lin算法是图划分问题中最简单、最知名的启发式算法之一,由于传统的Kernighan-Lin算法在图划分问题上很难提高其执行效率,因此,本文基于传统算法的思想与图划分问题研究后,提出了对Kernighan-Lin算法的改进算法。最后,采用空手道俱乐部数据集为实验数据,实验结果证明了改进算法的有效性和可行性。
关键词 :Kernighan-Lin算法,图划分,社交网络

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在信息时代中,随着互联网的使用规模不断扩大,我们需要面对各种各样的网络数据分析和处理,因此,大规模和复杂的图数据划分成了讨论中的热点,另外图信息隐藏技术 [1] 作为数据保护的措施之一,也离不开相应的图划分算法。图数据划分问题是经典的NP问题 [2] ,针对一个复杂的图数据,很难找出图划分的最优算法。从20世纪90年代初期至今,国内外研究者不断对图划分及相关问题进行了深入研究,提出了许多比较好的图划分算法,目前主要有谱方法、几何方法、启发式方法、智能优化算法、多层划分算法、混合方法等 [3] 。谱方法虽能划分不同类别,但计算量大,H. Simon和S. Barnard于1993年对谱方法进行了改进,具体是使用多层的谱二分(MSB)有效地减少了算法求解特征向量的执行时间。几何方法采用几何最优方式对图信息划分,虽速度快但划分效果不佳,1994年,S. Ranka和C. Ou提出了一种基于多维的空间填充曲线方法。备受关注和广泛使用的智能优化算法近年来一直用来解决图划分问题,例如模拟退火算法 [4] 、遗传算法 [5] 等。多层划分法是为了解决规模比较大的图而提出的,在文献 [6] 和文献 [7] 中,分别对该算法都进行了不同程度的改进。Kernighan-Lin算法是一种比较典型的基于启发式规则的求解策略 [8] 。它的主要思想是先将一个图随机化分成两个已知大小群组,然后交换任意两个顶点使得两个群组之间的割集规模最小,从而得到割集规模最小后的两个群组。该算法通常处理一万个顶点以内的图。M. Fiduccia和M. Mattheyses提出的Fiduccia-Mattheyses (FM)算法对Kernighan-Lin算法进行了改进。FM算法采用单点移动,并引入了桶列表数据结构,减少了时间复杂度。该类方法不需要知道节点的坐标信息,而是需要根据节点之间的连接信息进行划分。2000年,S. Dutt和W. Deng从顶点的移动次数对FM算法进行了改进。2002年,S. Dutt和W. Deng又从收益的计算方式进行改进。值得一提的是,Kernighan-Lin算法是一种典型的基于邻域搜索的路径改进算法,近年来,国内外学者以Kernighan-Lin算法为核心操作提出了Chained Kernighan-Lin [9] 、Kernighan-Lin Helsgaun [10] 和Multilevel Reduction [11] [12] 等多种宏启发式算法,不少学者对Kernighan-Lin算法的初始解构造和边交换策略等方面展开研究,试图提高算法求解性能。然而,目前对基于该启发式 Kernighan-Lin算法并没有系统的分析和评价,本文结合算法分析和实验验证,证明了改进LK算法在运算时间和运算效果方面都有很大的进步,同时根据分析实验结果,选择出最优方案。
2. 传统Kernighan-Lin算法及分析
Kernighan-Lin算法是由Brian Kernighan和Shen Lin在1970年提出的,是图划分问题中最简单、最知名的启发式算法之一 [13] 。核心思想是将n个图节点任意划分成指定规模的两个群组,对于任何由分属不同群组的节点i和节点j组成的顶点对(i, j),交换i和j的位置,并计算交换前后两个群组之间割集规模的变化量。在所有(i, j)对中找到使割集规模减小最多的顶点对,或者若没有使割集规模减小的顶点对,则找到使割集规模增加最小的顶点对,然后交换这个两个顶点。在交换的过程中,两个群组的节点数量都不变,因为一个节点离开某个群组时另一个节点加入该群组。因此,算法能够满足群组的规模与指定规模保持一致。然后重复上述过程,但一个重要的约束条件是群组中的每个节点只能移动一次。一旦某个节点和另一个节点交换过,那它将不会再次被交换(至少不会在本轮算法中再次被交换)。因此,在算法第二步中,考虑除第一步中交换过的两个节点之外的所有顶点对。接着算法继续运行,每一步都交换最大程度减少或最小程度增加群组之间边数的顶点对,直到没有可以交换的顶点对,此时本轮算法停止。若群组规模不相等,那么在较大规模群组中会有未被交换过的节点,其数量等于群组规模的差值。
Kernighan-Lin算法可描述为下面的步骤:
Step1:给定N个节点的图,随机划分图节点到两个指定规模大小的 群组;
Step2:分别从 群组中选择节点i和节点j组成顶点对(i, j),交换i和j的位置,并计算交换前后群组之间割集规模的变化量并记录该变化量P;
Step3:重复上步骤,已交换过的节点不再参与;
Step4:直到没有可以交换的顶点对,算法结束。
需要注意的是,在顶点对交换的过程中,P值并不一定是单调增加的。不过,即使某一步的交换会使P值有所下降,仍然可能在其后的步骤中出现一个更大的P值。当交换完毕后,便找到上述交换过程中所记录的最大的P值,这时对应的割集规模达到最优。
在上述Kernighan-Lin算法中,考虑了所有可能的节点对,从选择节点的角度分析,必须要让每个节点交换过,因此执行效率是比较低,其时间复杂度为 。
3. 改进算法及算法分析
3.1. 改进算法描述
在传统的Kernighan-Lin算法中,选择了所有可能的顶点对进行交换使割集规模达到最小。使得效率降低和时间复杂度变大。在改进算法中,最明显的是选择节点方式发生了改变,若同时分别从群组1和群组2中选择两个节点组成2 × 2轮循环,然后在2 × 2轮循环中选出使割集规模达到最小的顶点对 进行交换,其具体算法思想描述如下:
1) 按照要求随机分成两个群组V1和群组V2,其中 ,对群组V1和群组V2中的每个节点及其它对于群组V1和群组V2的度可以用一个三元组 来表示,V是对应的节点名, 表示节点V在群组V1中的度, 表示节点V在群组V2中的度,即 表示节点V与群组V1中的其它节点之间的连接边数; 表示节点V与群组V2中的其它节点之间的连接边数;且对于任意的节点V都有 ;
2) 当图 被划分为两个群组V1和群组V2后,对应的割集中边的数目为 ;
3) 目标是使得群组内的节点之间的边数最大,而群组之间的边数最小,即:
并且 ,但是由于 是个常数(m为图的总边数),因此函数 与 等价的,故可以选择 即割集边数最小化为目标函数;
4) 分别选择每个群组中外边数减去内边数最大的两个节点组成2 × 2个顶点对;
5) 选择四种交换中割集规模减少最大或者割集规模增加最少的作为最终的交换顶点对;即可能的四次变换中 减少最大或者增加最少;
6) 交换过的节点不再参与,直到无法在某个群组中找到可交换的两个节点,算法结束。
3.2. Kernighan-Lin改进算法节点度变化分析
在进行每一次节点 和 ( , )的交换后, , ,对应的节点度的变化如下:
1) 对于节点 和 , , 换成 和 ;
2) 对于 和 中其他节点 可以分为如下几种情况:
,则节点 的度情况 保持不变;
,则节点 的度情况 变为 ;
,则节点 的度情况 变为 .
3.3. 改进算法分析
本节对所提出算法的复杂度进行分析,本算法的复杂度主要体现在初始划分、节点选取以及选取之后的迭代时间,由于初始划分的随机性,节点选取平均次数为最小规模的群组的一半,即时间复杂度为
,每轮选取之后的迭代次数为4,总的轮数为节点选取次数。因此,整个算法时间复杂度约为 .而在传统的算法中,其时间复杂度大于 。改进算法一方面从时间复杂度有所突破,另一方面其执行效率也明显提高。
4. 实验
4.1. 实验方案与环境
本算法是利用初始划分信息的局部性,来实现划分效果。因此,实验效果与初始划分状态有关,首先在初始划分时是采用节点的随机分配,然后分析图节点的交换轮数和交换前后效果对比。
Zachary是通过对一个美国大学空手道俱乐部 [14] 进行观测而构建出的一个社交网络关系图 [15] 。如图1所示,图包含34个节点和78条边,其中个体表示俱乐部中的成员,而边表示成员之间存在的友谊关系,空手道俱乐部网络图已经成为图划分中的一个经典问题。因此本节选择Zachary空手道俱乐部网络图的数据集为实验数据,使得该实验更加具有合理性和充分性。

Figure 1. Karate club network
图1. 空手道俱乐部网络图
4.2. 实验结果与分析
在本文实验中,由于选择交换节点是改进算法的核心问题,不同的节点选择方式决定了算法的执行效率,因此,这里将给出三种选择节点的方法;方法一:分别从两个群组中各选择外边数减去内边数最大的两个节点进行交换;方法二:分别从两个群组中各选择外边数最大的两个节点交换;方法三:分别从两个群组中选择外边与内边比值最大的两个节点进行交换。
如图2所示,我们用了三种不同的寻找2 × 2个节点的方法,在选择2 × 2个节点时,曲线1表示每轮选择外边数减去内边数最大的两个节点进行交换,曲线2表示每轮选择外边最大的两个节点进行交换,而曲线3选择外边与内边比值最大的两个节点进行交换。由此,从图示不难看出,曲线1 (即本文提出的改进算法)比其他两种划分更具有优越性,在曲线1中,我们可以看出最少割集规模可达到10,也就是说,在图划分中,可达到部分聚类算法图划分后的割集规模。从曲线2可看出,它的执行轮数相比曲线1、3轮数为最少。且该选择节点的方法对图划分效果也是具有一定优越性。曲线3使用了节点的外边与内边之比来挑选2个节点。从曲线3上可得到,该方法的执行轮数与1方法差不多,但是效果不佳。
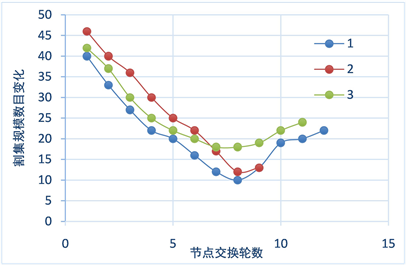
Figure 2. Changes between networks
图2. 割集规模变化
5. 结论
本文首先在Kernighan-Lin传统算法的基础上,提出了一种对传统算法的改进算法,在考虑其执行效率及时间复杂度的同时,综合考虑了改进算法对图划分的作用,并通过节点度变化的分析,验证了该改进算法的合理性,然后在本文提出的改进算法上,选择了Zachary空手道俱乐部网络图作为实验数据,并通过三种不同选择节点的方法进行了比较和分析,发现从两个群组中各选择外边数减去内边数最大的两个节点进行交换的节点选择方式比其他两种方法更加合理,实验结果验证了本文算法的有效性和优越性,为用户针对不同的图划分问题选择合适的划分算法提供了一定的借鉴作用。
文章引用
郁 湧,阚世林,赵 娜,骆永军,顾 捷,宋晨明. Kernighan-Lin算法的改进对图划分问题的研究
Research on the Improvement of Kernighan-Lin Algorithm for Graph Partitioning[J]. 计算机科学与应用, 2019, 09(05): 849-854. https://doi.org/10.12677/CSA.2019.95095
参考文献
- 1. 张军, 熊枫, 张丹. 图像隐写分析技术综述[J]. 计算机工程, 2013, 39(4): 165-168.
- 2. 李琪, 钟将, 李雪. 基于启发策略的动态平衡图划分算法[J]. 计算机研究与发展, 2017(12): 2834-2840.
- 3. 郑丽丽. 带权图的k划分算法研究[D]: [硕士学位论文]. 天津: 天津工业大学, 2013.
- 4. 许金凤, 董一鸿, 王诗懿, 等. LGP-SA: 分布式环境下基于模拟退火的大规模图划分算法[J]. 电信科学, 2016, 32(2): 83-91.
- 5. 姜火文, 曾国荪, 胡克坤. 一种遗传算法实现的图聚类匿名隐私保护方法[J]. 计算机研究与发展, 2016, 53(10): 2354-2364.
- 6. Saab, Y.G. (2004) An Effective Multilevel Algorithm for Bisecting Graphs and Hypergraphs. IEEE Transactions on Computers, 53, 641-652. https://doi.org/10.1109/TC.2004.3
- 7. Benlic, U. and Hao, J.K. (2011) A Mul-tilevel Memetic Approach for Improving Graph k-Partitions. IEEE Transactions on Evolutionary Computation, 15, 624-642. https://doi.org/10.1109/TEVC.2011.2136346
- 8. 曾华, 崔文, 付连宁, 等. Lin-Kernighan算法初始解的启发式构造策略[J]. 山东大学学报(工学版), 2012, 42(2): 30-35.
- 9. Pellegrini, F. and Roman, J. (1996) Scotch: A Software Package for Static Mapping by Dual Recursive Bi-Partitioning of Process and Architecture Graphs. In: Proceedings of HPCN Europe, Springer, Berlin, 493-498. https://doi.org/10.1007/3-540-61142-8_588
- 10. Simon, H.D. (1991) Partitioning of Unstructured Problems for Parallel Pro-cessing. Computing Systems in Engineering, 2, 135-148. https://doi.org/10.1016/0956-0521(91)90014-V
- 11. Karypis, G. and Kumar, V. (1998) Multilevel K-Way Partitioning Scheme for Irregular Graphs. Journal of Parallel and Distributed Computing, 48, 96-129. https://doi.org/10.1006/jpdc.1997.1404
- 12. Grady, L. and Schwartz, E.L. (2006) Isoperimetric Graph Partitioning for Image Segmentation. IEEE Transactions on Pattern Analysis & Machine Intelligence, 28, 469-475. https://doi.org/10.1109/TPAMI.2006.57
- 13. Kernighan, B.W. and Lin, S.A. (1970) Efficient Heuristic Procedure for Partitioning Graphs. Bell System Technical Journal, 49, 291-307. https://doi.org/10.1002/j.1538-7305.1970.tb01770.x
- 14. 李孔文, 顾庆, 张尧, 等. 一种基于聚集系数的局部社团划分算法[J]. 计算机科学, 2010, 37(7): 46-49.
- 15. 杨艳萍. 基于双向加权图的社交网络用户可信度算法研究[J]. 信息网络安全, 2017, 17(7): 40-44.