Computer Science and Application
Vol.
09
No.
11
(
2019
), Article ID:
32849
,
7
pages
10.12677/CSA.2019.911223
Volume Data Classification Visualization Based on Probabilistic Classification Model
Junda Zhang*, Xiao’an Tang
National University of Defense Technology, Changsha Hunan

Received: Oct. 16th, 2019; accepted: Oct. 31st, 2019; published: Nov. 7th, 2019

ABSTRACT
Classification visualization is an important method for volume data study, which can intuitively reveal the structural characteristics. This paper proposes a classification visualization method based on probabilistic classification model. First, the voxel probabilistic classification model is established, which realizes the classification of voxel with the transfer function defined in gray histogram. Then voxel probabilistic classification model and kernel regression are combined to achieve more accurate reconstruction result, and the validity of reconstruction on reconstructed points is measured. Finally, from gray value to color and opacity, the visualization mapping based on reconstruction validity is implemented to obtain the final visualization result. The experiment shows that the proposed method can efficiently separate the feature structures of volume data and achieve a better classification visualization result of homogeneous continuity and heterogeneous separation.
Keywords:Volume Rendering, Ray Casting, Transfer Function, Classification Visualization, Kernel Regression
基于概率分类模型的体数据分类可视化
张俊达*,汤晓安
国防科技大学,湖南 长沙

收稿日期:2019年10月16日;录用日期:2019年10月31日;发布日期:2019年11月7日

摘 要
分类可视化能够直观表达体数据的结构特征,是研究体数据的重要方法。本文提出一种基于概率分类模型的体数据分类可视化方法。该方法首先建立体素的概率分类模型,利用灰度直方图中定义的传递函数实现体素的分类。然后将概率分类模型与核回归重构相结合,获得更加准确地重构结果,并构造重构点的重构有效性。最后结合重构有效性实现从灰度值到颜色、不透明度的可视化映射,得到最终的绘制结果。实验表明,本文方法能够有效区分体数据中的不同结构特征,形成同质连续、异质分离的绘制结果,实现较好的分类可视化效果。
关键词 :体绘制,光线投射法,传递函数,分类可视化,核回归

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
体数据主要由不同传感器在三维物理空间采样或科学计算等方式获取,因此在不同的应用领域,体数据可能表示为标量场,如温度、压强等,也可能表示为矢量场,如飓风数据、磁场数据等。对原始数据的直接研究缺乏直观性和启发性,而分类可视化通过对不同结构、特征的分类,能够更好地暴露体数据的分布规律,帮助研究者挖掘数据中蕴含的信息,增强可视化结果的表达能力,对体数据的研究具有重要意义。
分类可视化方法主要分为三类:基于传递函数的方法、基于统计的方法和基于标记的方法。在基于传递函数的方法中,Tian等利用交互的传递函数进行海洋涡流的可视化 [1],通过修改传递函数来提取二维、三维的涡流特征。Ma等提出了一种基于聚类和特征可见性度量的传递函数交互设计算法 [2]。Lan等将空间连接计算整合进基于二维传递函数的体数据分类中 [3],获得了较好的结构分离效果。Kawamura等设计了一种面向多变量的多维传递函数生成方法 [4],该方法不但能够实现多变量的体数据可视化,还可以兼容面绘制等传统绘制技术。基于传递函数的体数据分类方法仅仅从可视化映射阶段实现了体数据的分类,对于结构化体数据,特别是均匀网格体数据能够得到良好的结果,但当面向空间分布不均匀的非结构化体数据时,会产生诸多绘制失真和错误,并且该类方法不能实现体素的分类。基于统计的体数据分类方法的理论基础为决策理论和概率模型,能够实现体素的分类,被大量应用于数据预分类和离线分类算法。McGivney等通过贝叶斯框架提出一种解决部分容积效应的方法,该方法通过采用迭代算法计算后验概率密度的最大后验估计,得到体素的主要成分,实现体素的分类 [5]。Prilepov等利用体素的混合模型进行二元决策边界的提取,实现混合物质边界的重构和表示 [6]。基于标记的体数据分类方法通过在空间上限制传递函数对体数据的作用,减小了传统方法容易引起的绘制结果失真,可以实现光滑、二元的边界决策。Liang等设计了一种基于标记的交互体绘制方法 [7],用户选择感兴趣的区域后,算法将重新调整传递函数并优化感兴趣区域的绘制质量。然而该类方法没有考虑到边界周围的信号退化问题,因此在面对含有大量不确定性的体数据时,基于标记的体数据分类方法反而会产生更多的失真和错误分类的情况。
本文提出一种基于概率分类模型的体数据分类可视化方法,通过核回归将体素概率分类模型引入体数据重构,然后基于构造的重构有效性,实现重构点的可视化映射,采用光线投射法获得体数据的分类可视化结果。
2. 体素的概率分类模型
设体数据表示为 ,其中 为第i个数据点的空间坐标, 为对应的属性值。由于测量设备和测量环境的限制以及部分容积效应的影响,单一体素可能对应多种特征。为了描述这种情况,定义:
(1)
表示灰度值为y的数据点属于特征类 的概率为 。
灰度直方图能够描述体数据的灰度值分布规律,传递函数定义了从灰度值向颜色、不透明度的映射。本文使用bin宽度为1的灰度直方图结合传递函数的方法构建体素概率分类模型,如图1所示。

Figure 1. Voxel probability classification based on gray histogram
图1. 基于灰度直方图的体素概率分类
其中,红、蓝、绿色梯形为颜色映射,折线为不透明度映射 。本文用不透明度映射定义体数据特征, 分别表示两个特征类,不透明度值可以反映某一灰度值属于某一特征的条件概率,不透明度值大表示该灰度值属于某一特征的条件概率大。为了将条件概率从不透明度映射中分离,定义:
(2)
其中, 为对应第k个特征的最大不透明度。本文采用文献 [8] 的方法,引入“空”特征类,将没有定义传递函数的部分都归入这个特征类里面,从而使概率模型完整。最终,体素的概率分类模型表示为:
(3)
其中, , 即为上述的“空”特征类。
本文采用光线投射法实现体数据的分类可视化。该方法通过从视点向体数据引多条射线,射线在体数据内部进行重构采样,然后将采样值可视化映射为颜色和不透明度,最后将一条射线上的光学属性值进行叠加,形成这条射线最后表示的颜色和不透明度值。光线投射法不受体数据结构的限制,能够得到较好的绘制结果。
3. 面向分类的核回归重构
核回归方法作为一种常用的非参数估计方法,能够很好地适应上述概率分类模型。对任意一点 处的重构可以表示为:
(4)
其中, 为重构结果, 为空间核函数, 为重构的支撑域, 为支撑域内数据点的灰度值。式(4)表示任意一点的灰度值可以由支撑域内数据点灰度值的线性组合得到。定义空间核函数为:
(5)
其中, 表示重构点 与数据点 的距离,一般取 。
为了使核回归方法能够适应概率分类模型,本文定义特征核函数 。将两种核函数组合为最终的重构核,得到面向分类的核回归重构,体数据中任意一点对应特征 的重构灰度值为:
(6)
其中, 体现数据点 对重构点 的影响程度,距离重构点越近的数据点其对应的空间核函数越大,对重构的贡献越大。 体现概率分类模型对重构的影响,面向某一特征类 ,如果数据点属于此类的条件概率越大,则该点对重构的贡献越大。
4. 可视化映射
本文采用了固定支撑域的核回归重构方法,在数据密度不同的区域,重构的准确性是不同的。为了描述某一次重构的有效性,由式(6)中的两种重构核定义:
(7)
可以描述为在特征 的前提下,支撑域 范围内,对位置 重构时的重构有效性。
为了对分类结果进行有效的可视化表达,需要将重构的属性值根据给定的传递函数映射为光学属性。对于任意的空间位置 ,给定K个特征类,则需要对 进行K次重构,得到分别对应每个特征类的重构结果。本文沿用文献 [9] 的方法,采用累加混合的方式得到重构点对应的光学属性值。某一条射线上的重构点,采用从后向前的合成方式:
(8)
其中, 和 为累加的颜色和不透明度, 和 为根据给定的传递函数得到的当前位置的颜色和不透明度。通过在不透明度累加中加入 的权重,实现基于重构有效性的可视化映射。由于 与特征相关,因此式 与重构一样也需要进行K次。
5. 仿真结果及分析
为了验证本文算法的有效性,采用Tooth (数据来自GE Aircraft Engines,Evendale)和Engine (数据来自General Electric)两组数据,对比算法为基于传递函数的分类方法,均采用一维传递函数, 。

Figure 2. The transfer function of Engine dataset
图2. Engine数据的传递函数
Engine数据的传递函数如图2所示,基于传递函数的分类方法采用基本的最小二乘重构,传递函数对应的最大颜色值和不透明度都为1。为了对比在相同的颜色映射下的体数据分类结果,本文算法也采用图2所示的传递函数,其中不透明度映射同时定义了三个特征类。
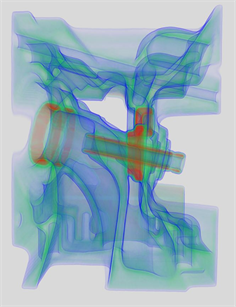
Figure 3. The classification visualization result of Engine dataset
图3. Engine数据分类可视化结果
Engine数据的可视化结果如图3所示。基于传递函数的分类可视化方法(左图)由于无法实现体素的分类,仅仅从可视化映射阶段对体数据定义的特征类进行颜色和不透明度的映射。在重构过程中产生的大量中间灰度值,使分类可视化产生类似平滑滤波的结果,不同特征之间的空间关系被模糊,特征类不能被清晰地可视化表达。本文算法(右图)由于引入了体素的概率分类模型,实现了同质区域内连续,不同物质间分离的重构结果。同时,考虑到体数据空间分布的不均匀性,构造了能够结合体素概率分类模型的重构有效性 。在进行可视化映射时,结合重构有效性进行光学属性的叠加,使最终的可视化结果能够清晰地可视化表达不同特征类。

Figure 4. The transfer function of Tooth dataset
图4. Tooth数据的传递函数
对于Tooth数据,传递函数如图4所示,对应的三种特征类依次映射为红色、绿色和蓝色,相应的不透明度映射与颜色映射的对应位置相同,对于归一化后的颜色和不透明度表示,传递函数对应的最大颜色值和不透明度都为1。其中蓝色部分对应的体数据并不是有效的体数据,但为了验证算法的有效性,依然将其定义为一个特征类,但蓝色和其对应的不透明度的最大值减小为0.7。

Figure 5. The classification visualization result of Tooth dataset
图5. Tooth数据分类可视化结果
Tooth数据的可视化结果如图5所示。与Engine数据的可视化结果类似,基于传递函数的分类可视化结果(左图)出现了特征类结构不清晰的问题,并且可见在牙齿结构表面覆盖的一层蓝色非有效数据出现许多“毛刺”,这是由传统重构方法产生的中间灰度值进入了用户定义的传递函数范围而引起的。本文算法(右图)的绘制结果中,蓝色的物质均匀地覆盖在牙齿结构表面,并且牙齿内部不同的特征类也非常清晰地得以表达。
6. 总结
本文提出了一种基于概率分类模型的体数据分类可视化方法。该方法首先利用灰度直方图中的传递函数定义了体素的概率分类模型。然后将概率分类模型引入到重构阶段中,基于核回归,实现了面向体数据分类的数据重构。最后,构造了重构有效性,并将其引入可视化映射阶段,最终得到了清晰、准确的体数据分类可视化结果。
文章引用
张俊达,汤晓安. 基于概率分类模型的体数据分类可视化
Volume Data Classification Visualization Based on Probabilistic Classification Model[J]. 计算机科学与应用, 2019, 09(11): 1986-1992. https://doi.org/10.12677/CSA.2019.911223
参考文献
- 1. Tian, F., Cheng, L., and Chen, G. (2018) Transfer Function-Based 2d/3d Interactive Spatiotemporal Visualizations of Mesoscale Eddies. International Journal of Digital Earth, No. 11, 1-21. https://doi.org/10.1080/17538947.2018.1543364
- 2. Ma, B. and Entezari, A. (2017) Volumetric Feature-Based Classification and Visibility Analysis for Transfer Function Design. IEEE Transactions on Visualization and Computer Graphics, 24, 3253-3267. https://doi.org/10.1109/TVCG.2017.2776935
- 3. Lan, S.R., Wang, L.S., Song, Y.P., Wang, Y.-P., Yao, L.P., Sun, K., Xia, B. and Xu, Z. (2017) Improving Separability of Structures with Similar Attributes in 2d Transfer Function Design. IEEE Transactions on Visualization and Computer Graphics, 23, 1546-1560. https://doi.org/10.1109/TVCG.2016.2537341
- 4. Kawamura, T., Idomura, Y., Miyamura, H. and Takemiya, H. (2017) Algebraic Design of Multi-Dimensional Transfer Function Using Transfer Function Synthesizer. Journal of Visu-alization, 20, 151-162. https://doi.org/10.1007/s12650-016-0387-1
- 5. Mcgivney, D., Deshmane, A., Jiang, Y., Ma, D., Badve, C., Sloan, A., Gulani, V. and Griswold, M. (2018) Bayesian Estimation of Multicomponent Relaxation Parameters in Magnetic Resonance Fingerprinting. Magnetic Resonance in Medicine, 80, 159-170. https://doi.org/10.1002/mrm.27017
- 6. Iuri, P., Harald, O., Eduard, D., Christoph, G. and Joy, K. I. (2013) Cubic Gradient-Based Material Interfaces. IEEE Transactions on Visualization & Computer Graphics, 19, 1687-1699. https://doi.org/10.1109/TVCG.2013.16
- 7. Liang, Z. and Hansen, C. (2013) Transfer Function Design Based on User Selected Samples for Intuitive Multivariate Volume Exploration. IEEE Pacific Visualization Symposium, 27 Feburary-1 March 2013, 73-80.
- 8. Beaucoup, F. and Carraro, L. (2007) Uncertainty Visualization in Medical Volume Rendering Using Probabilistic Animation. IEEE Transactions on Visualization & Computer Graphics, 13, 1648-1655. https://doi.org/10.1109/TVCG.2007.70518
- 9. Cai, W. and Sakas, G. (2010) Data Intermixing and Multi-Volume Rendering. Computer Graphics Forum, 18, 359-368. https://doi.org/10.1111/1467-8659.00356