Computer Science and Application
Vol.
13
No.
03
(
2023
), Article ID:
62591
,
15
pages
10.12677/CSA.2023.133031
基于两阶段服务与重试空间的故障可修P2P 网络系统分析
张羽康
燕山大学理学院,河北 秦皇岛
收稿日期:2023年2月11日;录用日期:2023年3月8日;发布日期:2023年3月16日

摘要
对于移动P2P网络这样高分布式异构的环境而言,为了较好地实现各终端系统协同合作和资源共享的目标,维护和提高网络的性能,构建一个性能良好的网络拓扑是研究的关键,本文针对这一特性,基于半分布式拓扑与完全分布式拓扑相结合的混合移动网络模型,建立了带有重试空间与工作故障的两阶段排队模型。利用拟生灭过程、矩阵几何解方法和Gauss-Seidel迭代法得到了网络模型稳态下的概率分布,给出了两阶段平均节点数等性能指标的表达式。利用编程软件进行数值试验,分析了参数对各指标的影响,通过构造系统单位时间平均费用函数与社会效用函数,求解最优参数,为移动P2P网络模型提供决策依据。
关键词
P2P网络,M/M/c排队,两阶段服务,矩阵几何解方法,社会效用函数

Analysis of Fault-Repairable P2P Network System Based on Two-Phase Service and Retry Space
Yukang Zhang
School of Science, Yanshan University, Qinhuangdao Hebei
Received: Feb. 11th, 2023; accepted: Mar. 8th, 2023; published: Mar. 16th, 2023

ABSTRACT
For a highly distributed heterogeneous environment such as mobile P2P network, in order to better achieve the goal of cooperation and resource sharing of various terminal systems, maintain and improve the performance of the network, building a network topology with good performance is the key to research, in view of this feature, based on the hybrid mobile network model combining semi-distributed topology and fully distributed topology, a two-stage queuing model with retry space and working fault is established. The probability distribution under steady-state of the network model is obtained by using the mimic-life and extinction process, the matrix geometric solution method and the Gauss-Seidel iterative method, and the expression of performance indicators such as the average number of nodes in the two stages is given. The numerical experiment is carried out by programming software, the influence of parameters on each index is analyzed, and the optimal parameters are solved by constructing the average cost function per unit time and the social utility function of the system, which provides a decision-making basis for the mobile P2P network model.
Keywords:P2P Networks, M/M/C Queue, Two Stage Services, Matrix Geometry Solution Method, Social Utility Function

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1.1. 文献综述
P2P (Peer-to-Peer)网络的分布式架构、匿名性以及开放性使其在互联网中得到快速稳定的发展,现己经成为组成互联网框架必不可少的基础。传统的网络一般使用C/S模型进行信息传送,也就是需要经过服务器获得文件,才能使用客户端进行相关的资源下载,而P2P网络不存在这两种角色的区分,每个节点都既可以是服务器又可以是客户端,且节点间都拥有各自自主的调节能力,相互之间不会依赖,现今P2P技术己在信息通信、资源共享、协同工作以及分布式计算等诸多领域具有广泛的应用。
Saied等 [1] 提出了反转蚁群优化(IACO)算法以改善对等体之间的负载平衡,作为基本蚁群优化(ACO)算法的一个变种,信息素对蚂蚁所选路径的影响是倒置的,蚂蚁从请求者对等体开始穿越图形,每个蚂蚁选择最佳对等体进行移动。Arunachalam等 [2] 提出了一个名为ABRW (地址广播随机行走)的新协议,作为一种轻量级的搜索方法,ABRW设计了底层拓扑的结构来解决P2P在MANETs上表现不佳的限制,用不同的基准搜索技术测量性能,证明其可以更好的适应非结构化体系结构。Luis等 [3] 设计了一个以Chord为顶层的两层层次结构,为分层分布式哈希表提供了一个具有可扩展覆盖管理的通用框架,并提出了一种构建分层分布式哈希表的方法,该方法能够很好地映射到互联网拓扑,并实现短的组内通信延迟。Lv等 [4] 研究了文件副本数量对非结构化P2P网络中搜索性能的影响,发现了当副本数量与文件请求率成正比时,搜索和下载时间都是最优的。Wu等 [5] 提出了一种使用P2P网络虚拟节点方法的动态负载再平衡算法,使静态索引方案更加实用和稳健,实验表明,所提出的分布式相似性索引方案对于高维空间相似性索引的负载平衡是有效和高效的。Zhou等 [6] 提出了一种新型的基于位置的对等体聚类机制和一种时间感知的节点选择方案,该方案采用了拉和推的方法,基于对等体每天经常重复移动的发现,以应对移动P2P城域网中对等体的移动问题。仿真结果表明,该资源搜索方案既可以提高搜索成功率,又可以减少传播的信息。
P2P网络节点共享和获取资源的随意性,使得节点都处于高度自治的状态,主动性很强,但底层网络连接的不可靠性和节点能力的异构性,使得网络中存在着大量的不安全因素,如不可靠服务和欺诈问题的存在。Meng等 [7] 为了提高GeTrust的可用性和防止恶意行为,提出了一种基于Chord的P2P网络信任模型、激励机制与匿名信誉管理策略。在该模型中,一个服务对等体需要为它将要提供的服务选择它的担保对等体,并且它们都需要为该服务保证信誉抵押。Wen等 [8] 为了衡量交易信誉和推荐信誉,引入了一个抵御虚假推荐和恶意节点协作欺骗影响的风险值,目标节点的全局信誉值可以通过使用交易信誉、推荐信誉和风险值的不同部分来计算。Lv等 [9] 通过模拟探索了Gnutella查询算法、数据复制策略和网络拓扑的各种替代方案,并提出了一种基于多次随机游走的查询算法,可以像Gnutella的泛洪方法一样快速地解决查询,同时在许多情况下将网络流量减少了两个数量级。Mohamed等 [10] 为了减少蠕虫的传播,使用了基于文件信任和基于对等信任的混合信任模型,在此模型中,请求节点首先检查所寻找文件的安全性,即文件信任,然后从拥有该文件的节点集合中选择信誉最好的节点,即基于节点的信任,从而进行下载。Meng等 [11] [12] 针对混合P2P网络提出了一种超级对等保证信任模型speedTrust。考虑到服务和反馈的质量是直接影响信任模型可用性的最重要因素,在请求节点和超级节点之间建立了反馈保证关系,并在服务节点和超级节点之间建立了服务保证关系。后又提出了一个用于二层P2P网络的超级节点感知信任模型sureTrust,子网的超级对等体负责计算子网中对等体的信任,并且超级对等体的信任与其子网中对等体的信任相关。仿真结果表明此模型能够提高普通节点的下载成功率,抵御不同类型的攻击。
“搭便车”问题是指节点只索取不付出的行为,也就是只从其他节点获取资源,而不共享自己拥有的资源。搭便车现象造成了诸多不便,P2P之中可进行利用的资源不断缩减,随着用户数量的激增,用户的需求难以得到满足,出现“供不应求”的局面。Murat等 [13] 提出了一个不需要任何永久的对等体标识或安全基础设施的框架,在这个框架中,每个节点监控它的邻居,决定他们是否是搭便车并采取适当的行动。Sanjeev等 [14] 提出了一个基于排名的P2P系统,该系统收集了参与节点共享的数据的统计信息,定义了节点的排名以增加或减少该对等体上传或下载的数据的比率,并且促进节点共享资源以提高等级减少搭便车行为。Bhardwaj等 [15] 提出了基于Shamir的秘密共享(SSS)和使用可信对等体(TPs)的解决方案。在假设恶意节点的数量少于总数的一半的情况下,迫使任何节点将未受污染的内容转发给善意节点,以便不被驱逐。Abdulazeez等 [16] 提供了一个利用P2P网络非法分享受版权保护材料的在线社区“海盗”的案例研究,以研究自治机构在不太有利的条件下的稳健性,强调了自治社区为解决不利条件下的集体行动问题而制定的制度安排的多样性和共同性。
负载平衡是实现资源有效共享,提高系统资源有效使用率的必然要求,是影响系统有效运行与服务质量的重要因素之一,由于P2P网络中各节点相互平等且没有中心存在,传统基于中心服务器调度的负载平衡算法不适用,需根据P2P特性研究负载平衡算法。Colin等 [17] 设计并模拟了一个基于混合P2P和客户服务器两种架构的MMOG的静态和动态兴趣区管理,使用OPNET Modeler18.0来模拟和评估所提出的系统。Duan等 [18] 提出了一个三层的移动混合分层P2P (MHP2P)模型,并提供了一个负载平衡方案,使MHP2P的负载能够随着MEC服务器和查询负载的增加而得到良好的平衡。Dharmendra等 [19] 在P2P网络中开发了基于概率的负载平衡控制和安全增强算法。对等体的概率可以用鸡群优化(CSO)来计算以在P2P网络中选择最佳对等体与实现负载平衡与资源利用。
1.2. 文章概述
现存的排队论研究与应用中,大多与呼叫中心、银行与医院等场景相关,与P2P网络相结合的内容极少,但实际上在移动P2P系统中,大量节点在某一个时间点随机提出资源的搜索请求,在普通节点处形成资源请求队列,如果普通节点在一定时间内不能处理完这些请求,在该节点处就有可能出现请求队列拥塞现象,由于每个用户提出资源请求的行为是一种随机现象,因此运用随机排队理论的知识对这些请求节点队列进行深入分析和管理是很有必要的。本文针对移动P2P网络的特殊性,从移动P2P文件传输系统的服务能力出发,对P2P系统的性能进行建模和研究,利用排队理论研究移动P2P网络的资源传输与网络安全问题。基于混合移动网络拓扑模型,建立一个带有重试空间与工作故障的两阶段排队系统,来进一步优化P2P网络在文件传输过程中的不稳定性和下载拥塞等问题。
2. 移动P2P网络模型描述
移动P2P网络已经成为近年来研究热点领域之一。在移动P2P网络中,由于节点移动频繁,覆盖层无法保持相对持久的稳定性,会导致覆盖层与底层物理网络出现拓扑不匹配的情况,即拓扑匹配问题,这不但会引起资源查找和数据传输效率低下,而且也会导致较高的网络维护开销,浪费宝贵的无线带宽资源,因此,如何解决拓扑匹配问题,建立高效的资源查找策略是移动P2P网络研究的核心内容之一。本文以网关节点为媒介,将常见的完全分布式P2P网络和半分布式的P2P网络相结合 [20] ,如图1所示。
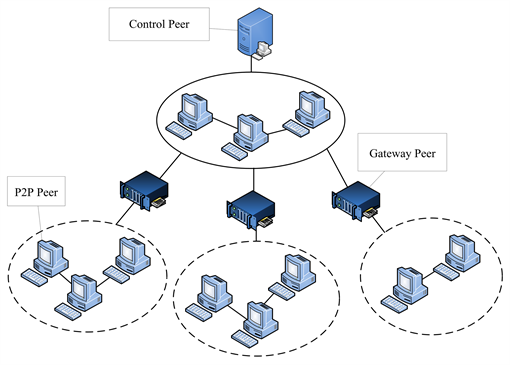
Figure 1. Schematic diagram of the mobile P2P network architecture
图1. 移动P2P网络结构示意图
该网络由控制节点、网关节点与普通节点结合而成,由于网关节点具有连接混合P2P网络与纯P2P网络的功能,因此该混合式网络拓扑可以同时保留纯P2P网络资源传输简单与混合P2P网络高效路由与安全性高的优点,并且弥补纯P2P网络缺乏有效地发现、路由与保护机制的缺点。
节点通过控制节点中的路由发现功能来找到通向目的节点的源路由,当请求节点发出资源请求时,系统首先在纯P2P网络中进行资源查询,若区域中存在该请求资源,请求节点将在纯P2P网络进行资源传输并离开系统,否则进行跨区域查询,并将请求资源的相关信息通过网关节点从控制节点转发至请求节点,该请求节点与之建立连接后进行数据传输。这种方法的一个优点是很容易找到通往目的节点的有效路由,因为控制节点掌握了整个网络的拓扑结构。而这种方法的缺点是缺乏可扩展性和容错性,因为对于大型对等网络来说,控制节点可能过载,并且整个网络将由于控制节点的故障而被破坏。
将请求节点的资源请求过程视为顾客的到达过程,普通节点与网关节点的查询与传输过程视为服务过程。将上述混合式P2P网络视为一个两阶段排队模型,第一阶段与第二阶段的系统中分别有c ( )个与1个服务节点。第一阶段服务系统由纯P2P网络的c个普通节点构成,与之相连的网关节点被视为第二阶段服务系统。当控制节点过载时会导致整个网络发生故障,同时假设修理工随时待机修理故障的服务节点。
1) 请求节点的到达过程为到达率为 ( )的泊松到达。该系统由两阶段服务节点串联组成,两阶段服务节点的服务时间均服从指数分布,服务率分别为 和 ,其中 。请求节点到达系统后进入第一阶段,在第一阶段接受完服务后以概率 ( )进入第二阶段接受服务,以 ( )离开系统。
2) 受控制节点的影响,两阶段的服务节点可能同时发生故障,故障期间第一阶段的服务节点将以低速率 进行服务,第二阶段的服务节点则完全故障。如果节点发生故障,则正在接受服务的节点中断服务,并到队首重新等待接受服务,已经服务过的时间无效。发生故障后立即进行修理,修理时间服从参数为 的指数分布。
3) 第二阶段的请求节点会因等待时间过长而感到不耐烦,设其耐心等待的时间限度服从参数为 的指数分布,当请求节点在第二阶段系统中等待时间超过限度时,将以概率 ( )进入重试空间等待,否则以 ( )离开系统。
4) 假设第一阶段服务系统的空间可以容纳无限个请求节点,第二阶段服务系统的空间最多容纳K个请求节点,当系统中请求节点数达到K时,请求节点则以概率 ( )进0入重试空间等待,否则以 ( )离开系统。
5) 假设重试空间最多容纳M个请求节点,当空间中请求节点数达到M时,将不再允许请求节点进入。重试空间中的每个顾客的重试间隔服从参数为 的指数分布。
6) 假设到达间隔、服务时间、修理时间与重试间隔相互独立,采用先到先服务(FCFS)排队规则。该网络运行机制如图2。
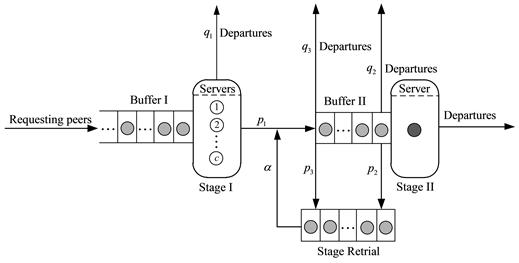
Figure 2. P2P network operation mechanism diagram
图2. P2P网络运行机制图
3. 模型分析
3.1. 状态转移矩阵
令 表示时刻t系统中第一阶段的请求节点数, 表示时刻t系统中第二阶段的请求节点数, 表示时刻t系统中重试空间的请求节点数, 表示时刻t系统中服务台的状态,具体如下:
从上述模型假设的分析,可以得到 为一个Markov过程,其状态空间为:
(1)
将状态按照字典序进行排列,系统的状态转移率矩阵可以写成如下形式:
(2)
并令 , ,其中 , , , 分别表示对应水平间的状态转移率矩阵。为了更简便的书写矩阵,我们定义如下的数学符号。
当 时,
, ,
当 时,
, ,
, .
当 时,
, .
当 时,
, ,
, .
当 时,
, .
为了表示 矩阵的子块矩阵,构造矩阵 、 、 、 并且这些矩阵均为2M + 2维的方阵。为了进一步表示上述方阵,引入 、 、 、 、 、 、 、 ,且这些矩阵均为二维方阵。
,
,
, ,
, , ,
, ,
, ,
,
.
当 时,
,
,
,
, , ,
,
,
, ,
, .
从而 矩阵的子块矩阵可表示如下,
,
当 时,
, ,
.
3.2. 系统稳态分析
由矩阵 的结构可知,Markov过程 是一个拟生灭过程
(quasi-birth-and-death process, QBD)。当Markov过程 正常返时,定义稳
态分布如下
(3)
其中 , 。
.
QBD 正常返的充分必要条件是矩阵方程
(4)
存在一个最小非负解 ,且谱半径 , 维随机阵
(5)
存在左零向量,当QBD是正常返时,稳态分布满足下列方程组
(6)
其中 是维数为 且所有元素均为1的列向量, 是维数为 的单位矩阵。
上述结论分析证明过程运用了矩阵几何解方法,其具体证明过程可参考文献 [21] [22] 。为了显式表示出系统的各项性能指标,需要求解上述矩阵二次方程(3)的最小非负解 的精确表达式,但是由于矩阵 , , 相对复杂并且维数很大,因此需要借助迭代方法获得矩阵二次方程(3)的最小非负解 的近似解,现存的方法中,文献 [22] [23] [24] [25] [26] 中所提到的方法们较经典且常用,包括牛顿迭代法、线性递进算法、修正边界算法与对数约化算法。在对 或其他与 相关的矩阵求解时,为提高收敛速度,一个标准的作法是考虑Newton序列,以很少的迭代次数达到精度尽可能低的要求,因此迭代速度亦优于牛顿,对于其他三种方法,理论上可认为修正边界算法渐近地快于线性递进算法,而对数约化算法的迭代次数等于线性递进算法迭代次数的对数,因此对数约化算法明显地优于线性递进算法,它比修正边界算法逼近得更快,因为后者是线性收敛的。而Gauss-Seidel迭代法大多用于线性方程组的求解,与上述方法相比具有收敛速度快的特点,因此本文采用了Gauss-Seidel迭代方法,获得矩阵二次方程(3)的最小非负解 的近似解,从而得到 的数值结果,详见表1。
Table 1. Gauss-Seidel iterative algorithm
表1. 高斯赛德尔迭代算法
3.3. 性能分析
在移动P2P网络模型稳态分布存在的条件下,通过分析我们可以得到系统的性能指标如下。
1) 系统中第一阶段、第二阶段与重试空间平均请求节点数为
,
,
.
2) 系统中第一阶段、第二阶段处于正常服务状态与故障服务状态的服务节点数为
,
,
.
3) 系统中因空间满离去的概率、因不耐烦离去的概率为
4. 数值例子
根据QBD 正常返的充分必要条件是矩阵二次方程(4)存在一个最小
非负解 ,且谱半径 ,由此可假设该模型的参数。利用编程软件绘图,得到P2P系统性能指标随参数变化的关系图像,进而可以分析得到参数变化对性能指标的影响,从而为该P2P系统节点的调度策略提供依据,建立效用函数,优化系统。
4.1. 参数变化对P2P系统性能指标的影响
根据上述分析得到系统的性能指标,利用数值实验检验系统参数对系统性能指标的影响。假设 , , , , , , , , , , , ,以重试概率 和故障率 为变量,图3描述了 和 与第二阶段系统中平均队长 的关系。当 为定值时, 随 的增大而增大,这是因为 增大时,系统中第二阶段的服务节点无法提供资源传输工作,导致第二阶段中等待的请求节点增多,但随着等待请求节点的增加,由于不耐烦而离开的节点也随之增加,并且由于第一阶段中的服务节点服务率下降,导致第一阶段中接受完服务并进入第二阶段中等待的请求节点也减少,所以 的增长幅度逐渐减小。当 为定值时, 随 的增大先呈增大趋势,这是因为 增大导致从重试空间进入第二阶段等待的请求节点增加,但随着 继续增大, 逐渐减小,这是因为第二阶段中等待的请求节点增多,并且由于第二阶段的缓冲区有限,因此因不耐烦而离开系统或进入重试空间的请求节点也增加, 变小。
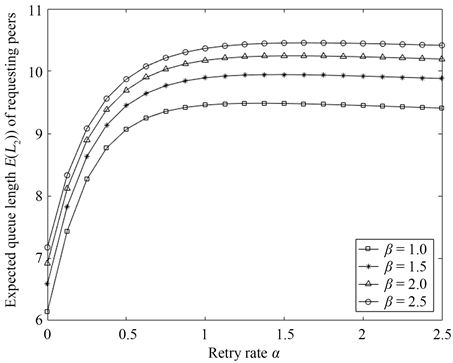
Figure 3. The relationship of with and
图3. 与 和 的关系
在图3的基础上,以修复率 和系统故障率 为变量,图4描述了 和 与重试空间中平均队长 的关系。当 为定值时, 随着 的增大而逐渐减小,这是因为 增大使 增大,第二阶段中等待的请求节点变少,由于缓冲区和不耐烦行为而离去的节点变少,重试空间中的节点也随之变小,但随着 的继续增大,第一阶段中接受完服务进入第二阶段中等待的节点数变多,因此减小的幅度变小。当 为定值时, 随着 的增大而增大,这是因为 增大使 降低,系统出现拥塞的可能性增大,第二阶段中由于不耐烦的节点而进入重试空间的节点变多。

Figure 4. The relationship of with and
图4. 与 和 的关系
在图3的基础上,假设 ,以系统故障率 和重试速率 为变量,图5描述了 和 与因空间满而离去系统的概率 的关系。当 为定值时, 随着 增大而增大,这是因为 增大使第二阶段中等待的服务节点变多,系统出现拥塞的可能性变大,缓冲区满载的概率变大,由于第二阶段缓冲区满载而进入重试空间的节点增多,重试空间中等待的请求节点变多,从而使 也变大,但随着 的继续变大,第一阶段中完成服务而进入第二阶段中等待的节点数变少,并且第二阶段中由于不耐烦离去的节点增多,从而第二阶段缓冲区满载的可能性变小,因此增大幅度变小,甚至出现下降的趋势。当 为定值时, 随着 的增大而减小,这是因为 变大使重试空间中的节点数变少,因重试空间满而离去系统的概率变小,但随着 继续增大,第二阶段中等待的节点数变多,因此因第二阶段缓冲区满而离去的概率增大,因此 减小的幅度由大变小。
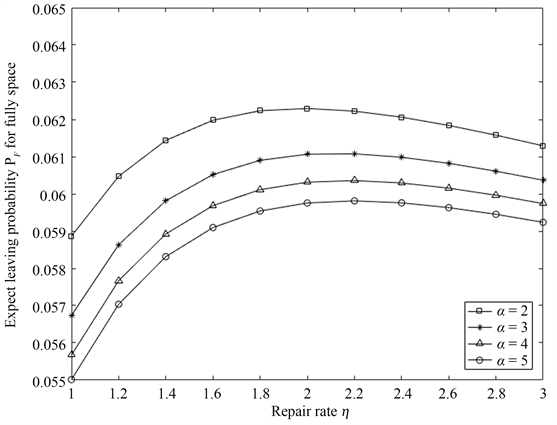
Figure 5. The relationship of with and
图5. 与 和 的关系
4.2. 社会最优策略
由4.1节的数值例子分析,系统的每一个参数都会影响系统的性能指标,利用上述性能指标的定义,建立单位时间内的平均费用函数。引入下列费用参数: 表示单位时间内每个请求节点进入第一阶段系统后由于延迟而等待的费用; 表示单位时间内每个请求节点进入第二阶段系统后由于延迟而等待的费用; 表示单位时间内每个请求节点进入重试空间后由于延迟而等待的费用; 表示单位时间内每个请求节点接受正常服务时的费用; 表示单位时间内每个请求节点接受故障服务的费用; 表示单位时间内每个服务节点处于空闲状态时的费用。
由此可得单位时间的平均费用函数
为了讨论社会最优策略,设r表示每个服务完成的节点获得的效用,则社会效用函数定义为
.
在图3的基础上,假设 , , , , , , 。通过改变第一阶段的服务率 和节点修复率 ,得到系统单位时间内社会收益U的变化情况,通过算法插值拟合得到图6。当 为定值时,U随 的增大而减少,当 为定值时,U随 的增大而增加。这是因为 较大时,系统的服务速率加快,系统单位时间花费的平均费用较少,所以社会效用较大;当 增加时,系统的平均等待的节点数,故障节点的数量减少,导致F减少,因此U变大。从图中可以看出,如果在 与 逐渐变小的情况下,U也将会随之变小,出现零点甚至负值的情况,因此要避免社会效用出现负值的情况。例如当系统中服务节点发生故障时,要适当提高 与 才能确保系统的社会效用更大,并且在假设条件下,社会效用存在最大值。
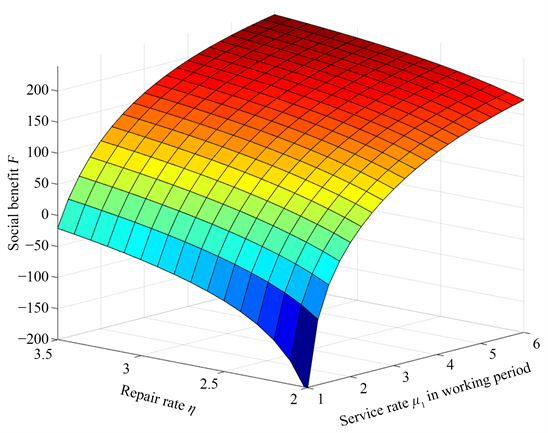
Figure 6. The relationship of U with and
图6. U与 和 的关系
5. 结论
本文在纯P2P网络与混合式P2P网络相结合的混合网络拓扑的基础上,将混合网络视为两阶段服务模型,将P2P系统中节点的资源请求与传输过程抽象为排队系统中的顾客到达与服务台服务过程,同时引入重试空间,加入同步故障与不耐烦顾客策略,建立带有重试空间的两阶段可故障M/M/c排队模型。通过构造四维连续Markov链,利用矩阵几何解方法得到网络模型的稳态分布、各阶段平均请求节点数、平均故障服务节点数与平均延迟等性能指标,通过数值实验,分析了参数对各指标的影响,对构造的平均费用函数与社会效用函数进行实验,在假设的参数条件下得到了最优参数,在此基础上得出了当服务节点发生故障时,适当提高服务率与修复率可以保障社会效用的结论,为网络模型的优化提供了决策依据。
文章引用
张羽康. 基于两阶段服务与重试空间的故障可修P2P网络系统分析
Analysis of Fault-Repairable P2P Network System Based on Two-Phase Service and Retry Space[J]. 计算机科学与应用, 2023, 13(03): 319-333. https://doi.org/10.12677/CSA.2023.133031
参考文献
- 1. Saied, A. and Kianoush, A. (2017) A Reliable Path between Target Users and Clients in Social Networks Using an In-verted Ant Colony Optimization Algorithm. Karbala International Journal of Modern Science, 3, 140-152. https://doi.org/10.1016/j.kijoms.2017.05.004
- 2. Arunachalam, A., Ravi, V., Krichen, M., et al. (2021) Mathe-matical Model Validation of Search Protocols in MP2P Networks. Computers, Materials, & Continua, 8, 1807-1829. https://doi.org/10.32604/cmc.2021.016692
- 3. Luis, G.E., Biersack, E.W., Ross, K.W., et al. (2008) Hierarchical Peer-to-Peer Systems. Performance Evaluation, 13, 643-657. https://doi.org/10.1142/S0129626403001574
- 4. Lv, Q., Cao, P., Cohen, E., et al. (2005) Analysis of Search and Replication in Unstructured Peer-to-Peer Networks. ACM SIGMETRICS Performance Evaluation Review, 33, 404-405. https://doi.org/10.1145/1071690.1064276
- 5. Wu, J.G., Shen, L. and Liu, L.F. (2020) LSH-Based Distributed Similarity Indexing with Load Balancing in High-Dimensional Space. The Journal of Supercomputing, 76, 636-665. https://doi.org/10.1007/s11227-019-03047-6
- 6. Zhou, S. and Meng, X.F. (2020) A Location and Time-Aware Resource Searching Scheme in Mobile P2P Ad Hoc Networks. The Journal of Supercomputing, 76, 6809-6833. https://doi.org/10.1007/s11227-019-03139-3
- 7. Meng, X.F. and Liu, D.X. (2018) GeTrust: A Guarantee-Based Trust Model in Chord-Based P2P Networks. IEEE Transactions on Dependable and Secure Computing, 15, 54-68. https://doi.org/10.1109/TDSC.2016.2530720
- 8. Wu, Y., et al. (2008) History and Recommendation-Based Trust Model in P2P Environment. Application Research of Computers, 25, 915-919.
- 9. Lv, Q., Cao, P., Cohen, E., et al. (2002) Search and Replication in Unstructured Peer-to-Peer Networks. Journal of Information Processing, 30, 258-259. https://doi.org/10.1145/511399.511369
- 10. Mohamed, A.G. and Najem, M. (2018) Hybrid Trust Model for Worm Mitigation in P2P Networks. Journal of Information Security and Applications, 43, 21-36. https://doi.org/10.1016/j.jisa.2018.10.005
- 11. Meng, X. (2018) SpeedTrust: A Super Peer-Guaranteed Trust Model in Hybrid P2P Networks. Journal of Supercomputing, 74, 2553-2580. https://doi.org/10.1007/s11227-018-2286-9
- 12. Meng, X. (2018) SureTrust: A Super Peer-Aware Trust Model for 2-Level P2P Networks. Peer-to-Peer Networking and Applications, 11, 619-631. https://doi.org/10.1007/s12083-017-0577-1
- 13. Murat, K., İbrahim, K. and Özgür, U. (2008) Counteracting Free Riding in Peer-to-Peer Networks. Computer Networks, 52, 675-694. https://doi.org/10.1016/j.comnet.2007.11.002
- 14. Sanjeev, S., Chiranjeev, K. and Prem, N. (2018) Ranking Based System to Reduce Free Riding Behavior in P2P Systems. Advances in Information and Communication Networks, 886, 165-177. https://doi.org/10.1007/978-3-030-03402-3_12
- 15. Bhardwaj, R., Dixit, V.S. and Upadhyay, A.K. (2009) On Mitigating Pollution and Free-Riding Attacks by Shamir’s Secret Sharing in Fully Connected P2P Systems. 2017 13th International Wireless Communications and Mobile Computing Conference, Valencia, 1-7.
- 16. Abdulazeez, S. (2018) Dynamic Load Balancing for Massively Multiplayer Online Games. Doctoral Thesis, Liverpool John Moores University, Merseyside. https://doi.org/10.1007/978-3-030-23712-7_25
- 17. Colin, H. (2017) Institutional Solutions to Free-Riding in Peer-to-Peer Networks: A Case Study of Online Pirate Communities. Computer Communications (Net-works), 1, 17-46.
- 18. Duan, Z., Tian, C., Zhang, N., et al. (2021) A Novel Load Balancing Scheme for Mobile Edge Computing. Journal of Systems and Software, 186, 1-26. https://doi.org/10.1016/j.jss.2021.111195
- 19. Dharmendra, K. and Mayank, P. (2022) An Optimal Load Balancing Strategy for P2P Network Using Chicken Swarm Optimization. Peer-to-Peer Networking and Applications, 15, 1-23. https://doi.org/10.1007/s12083-021-01259-3
- 20. Sumino, H., Ishikawa, N. and Kato, T. (2006) Design and Im-plementation of P2P Protocol for Mobile Phones. 4th Annual IEEE International Conference on Pervasive Computing and Communications Workshops, Pisa, 13-17 March 2006, 55-61. https://doi.org/10.1109/PERCOMW.2006.38
- 21. Tian, N.S. and Yue, D.Q. (2002) The Quasi-Birth-and-Death Process and Matrix-Geometric Solution. Science Press, Beijing. (In Chinese)
- 22. Neuts, M.F. (1981) Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach. Johns Hopkins University Press, Baltimore.
- 23. Neuts, M.F. (1981) Moment Formulas for the Markov Renewal Branching Process Advance Applied Probability. Advances in Applied Probability, 8, 690-711. https://doi.org/10.2307/1425930
- 24. Ramaswami, V. (1988) Nonlinear Matrix Equations in Applied Probability-Solution Techniques and Open Problems. SIAM Review, 30, 256-263. https://doi.org/10.1137/1030046
- 25. Isaacson, E. (1966) Analysis of Numerical Methods. John Wiley, Balti-more.
- 26. Neuts, M.F. (1986) The Caudal Characteristic Curve of Queues. Advances in Applied Probability, 18, 221-254. https://doi.org/10.2307/1427244
