Smart Grid
Vol.05 No.06(2015), Article ID:16521,8
pages
10.12677/SG.2015.56034
Simulation and Analysis of the Perfect Harmonic Cancellation Method for APF
Xin Kong, Baohua Wang
College of Automation, Nanjing University of Science and Technology, Nanjing Jiangsu
Received: Nov. 26th, 2015; accepted: Dec. 8th, 2015; published: Dec. 15th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Harmonic detection is one of the most important control strategies in active power filter (APF). When the grid voltage is under distorted or unbalanced circumstance, the harmonic detection of APF causes error using the conventional harmonic detection methods, and the compensation effect is unsatisfactory. The compensating current equation of the perfect harmonic cancellation (PHC) is derived based on Instantaneous Reactive Power Theory in the paper. The PHC method uses positive sequence components of the grid voltage without the effect of distortion and unbalance while detecting harmonic. It makes for error reduction. Finally, the PHC method is simulated in the paper when the grid voltage is under normal circumstance or distorted and unbalanced circumstance. The simulation results verify that the APF using the PHC method has more satisfied compensation effect when the grid voltage is under distorted and unbalanced circumstance, and it proves that the PHC method is correct and superior.
Keywords:Active Power Filter, Harmonic Detection, Instantaneous Reactive Power Theory, The Perfect Harmonic Cancellation (PHC)

APF中完美谐波消除法的仿真与分析
孔昕,王宝华
南京理工大学自动化学院,江苏 南京

收稿日期:2015年11月26日;录用日期:2015年12月8日;发布日期:2015年12月15日

摘 要
谐波检测是有源电力滤波器(Active Power Filter, APF)的重要控制策略之一,当电网电压不平衡或畸变时,采用传统谐波检测方法会导致APF的谐波检测产生误差,最终的补偿效果变差。本文基于瞬时无功功率理论,推导了完美谐波消除法(Perfect Harmonic Cancellation, PHC)的补偿电流计算公式。PHC法检测谐波时提取了电网电压的正序基波分量,排除电网不平衡和畸变的影响,减小了谐波检测的误差。最后,本文对PHC法进行仿真验证,分别仿真了电网电压正常和电网电压畸变或畸变的情况,并与传统的p-q法和d-q法的补偿效果进行对比,证明了在电网电压不平衡或畸变的情况下,采用PHC法的APF具有更理想的补偿效果,验证了PHC法的正确性和优越性。
关键词 :有源电力滤波器,谐波检测,瞬时无功功率理论,完美谐波消除法

1. 引言
电力技术的发展为现代工业和人民生活带来巨大利益和便利,同时,它的非线性冲击性以及不平衡性给公用电网带来了大量谐波污染和无功问题,使得电能质量产生了明显的恶化。另一方面,由于数量众多的敏感设备接入电网进行使用,例如计算机,用户对公用电网的电能质量有着越来越高的要求。有源电力滤波器(Active Power Filter, APF)的出现能够很好的抑制和补偿谐波电流[1] -[8] 。
APF的控制策略包括以下两个环节:谐波检测和电流控制。谐波检测是解决谐波问题的一个重要手段[9] ,对抑制谐波有着重要的指导作用,是众多国内外学者致力研究的目标。基于此,国内外学者提出了诸多谐波检测的方法,时域中常用的方法包括基于三相瞬时无功功率理论的p-q法 [10] 、同步旋转坐标法(d-q法)和完美谐波消除法(Perfect Harmonic Cancellation, PHC) [11] [12] 等。其中p-q法在电网电压畸变或负载不对称时,无法有效地检测出谐波电流。在电网电压畸变或不对称时,d-q法的检测效果优于p-q法,但是补偿效果仍不理想。PHC法检测谐波时,以电网电压中的正序基波分量为基准,排除了电网电压畸变或者不对称带来的不利影响,补偿效果较好。
本文结合APF的工作原理,在瞬时无功功率理论的基础上推导出PHC法的补偿电流公式,然后搭建Matlab/Simulink仿真模型验证PHC法的优越性。
2. PHC法补偿电流推导
本文并联型APF为例,其结构如图1所示。并联型APF通过采样负载电流 来进行实时地计算,检测并提取出谐波分量
来进行实时地计算,检测并提取出谐波分量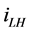 ,然后运用电流控制技术,使输出与谐波大小相同但方向相反的补偿电流
,然后运用电流控制技术,使输出与谐波大小相同但方向相反的补偿电流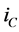 ,由于
,由于 ,其中
,其中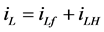 ,使电源电流
,使电源电流 等于负载电流的基波分量
等于负载电流的基波分量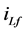 ,这样就可以补偿掉谐波[13] 。
,这样就可以补偿掉谐波[13] 。
谐波检测的目标是提取负载电流中的谐波分量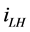 ,传统的谐波检测方法有基于瞬时无功功率理论的p-q法,以及来源于电机控制中dq变换的d-q法,PHC法是对p-q法以及d-q法的改进,它的目标是要消除所有的谐波电流以及基波无功功率,同时补偿不平衡,使得补偿后的电源电流对称正弦。如图2所示为三相并联APF的框图,设该电路中三相电压正序基波分量的瞬时值分别为
,传统的谐波检测方法有基于瞬时无功功率理论的p-q法,以及来源于电机控制中dq变换的d-q法,PHC法是对p-q法以及d-q法的改进,它的目标是要消除所有的谐波电流以及基波无功功率,同时补偿不平衡,使得补偿后的电源电流对称正弦。如图2所示为三相并联APF的框图,设该电路中三相电压正序基波分量的瞬时值分别为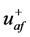 、
、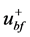 和
和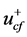 。将三相电网电压的正序基波分量变换到α-β坐标系下可得:
。将三相电网电压的正序基波分量变换到α-β坐标系下可得:
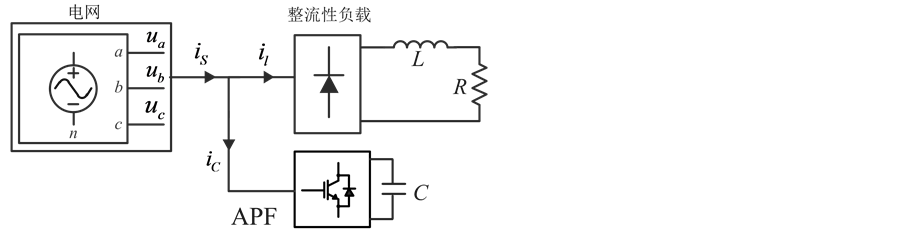
Figure 1. Main circuit of shunt APF
图1. 并联型APF系统结构
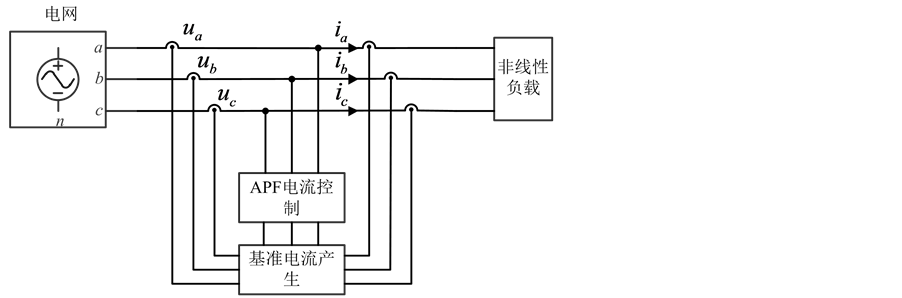
Figure 2. Structure diagram of APF
图2. APF结构框图
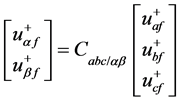 (1)
(1)
其中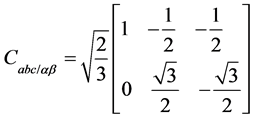 。
。
因此根据瞬时无功功率理论可以得出负载的瞬时有功分量p以及瞬时无功分量q:
 (2)
(2)
其中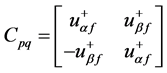 ,
, 、
、 为负载电流在α-β坐标系下的值。p、q可以分别表示为直流分量
为负载电流在α-β坐标系下的值。p、q可以分别表示为直流分量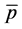 、
、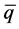 与交流分量
与交流分量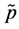 、
、 之和,由此式(2)可化为:
之和,由此式(2)可化为:
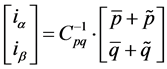 (3)
(3)
根据瞬时无功功率理论,当APF需要同时补偿谐波及无功时,负载侧参考电流为:
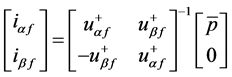 (4)
(4)
因此,PHC法的补偿电流在α-β坐标系的等效值为:
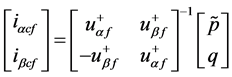 (5)
(5)
观察式(5)可以发现,PHC法的补偿电流采用电网电压的正序基波分量进行计算,当电网电压发生畸变或者不平衡时,正序基波分量保持不变,补偿电流的基准值不受影响。PHC法在电网电压畸变或者不平衡时,有很好的补偿效果。
3. 仿真与分析
3.1. Matlab/Simulink仿真模型
本文使用Matlab/Simulink对三相三线APF的谐波检测方法进行建模,在不同的电网电压和负载条件下进行仿真,将PHC法与d-q法和p-q法的补偿效果进行对比。图3为d-q法仿真模型,图4为PHC法仿真模型,图5为p-q法仿真模型。
3.2. 三相电网电压正弦对称
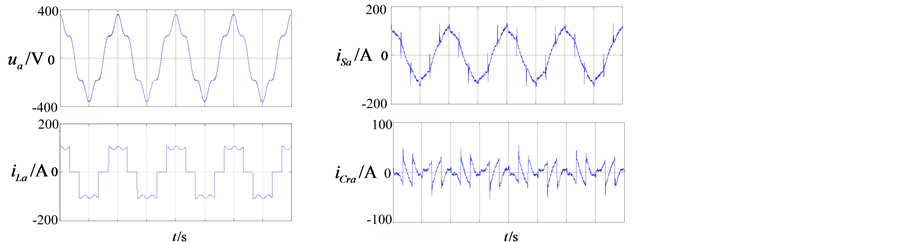
在三相电网电压正弦对称的条件下,补偿前A相电网电压、负载电流的仿真波形如图6(a)所示,图6(b)~(d)为分别使用三种谐波电流检测方法补偿后,电网电流、补偿电流的波形图。
仿真参数如下:三相电网电压为220 V/50 Hz,非线性负载为三相整流之后接2 mH电感和5欧电阻。使用powergui模块中的FFT Tools来测量THD,测得补偿之前负载电流THD为30.57%,使用d-q法、PHC法、p-q法补偿后电网电流的THD分别为9.91%、7.16%、8.42%。
从以上仿真波形和结果可以看出,当电网电压正弦对称时,三种算法均达到了不错的补偿效果。
3.3. 三相电网电压含有谐波对称
在三相电网电压含谐波对称的条件下,补偿前的A相电网电压、负载电流的仿真波形如图7(a)所示,图7(b)~(d)为分别使用三种谐波电流检测方法补偿后,电网电流、补偿电流的波形图。
仿真参数如下:三相电网电压为三相220 V/50 Hz并加入35.4 V/250 Hz的三相谐波,负载为三相整流之后接2 mH电感和5欧电阻。使用powergui模块中的FFT Tools来测量THD,测得补偿前负载电流THD为31.51%,使用d-q法、PHC法、p-q法补偿后电网电流的THD分别为12.61%、7.89%、20.12%。
从以上仿真波形和结果可以看出,当电网电压含有谐波的时候,p-q法的谐波补偿效果很不理想,PHC法比较理想。
3.4. 三相电网电压含有谐波不对称
在三相电网电压含谐波不对称的条件下,补偿前的ABC相电网电压、ABC相负载电流的仿真波形如图8(a)所示,图8(b)~(d)为分别使用三种谐波电流检测方法补偿后,电网电流、ABC三相补偿电流的波形图。
仿真参数如下:三相电网电压为A、C相220 V/50 Hz,B相141 V/50 Hz并加35.4 V/250 Hz三相谐波,非线性负载为三相整流之后接2 mH电感和5欧电阻。使用powergui模块中的FFT Tools来测量THD,测得补偿前负载电流THD为29.00%,使用d-q法、PHC法、p-q法补偿后电网电流的THD分别为11.41%、7.99%、26.22%。
从以上仿真波形和结果可以看出,PHC法效果比较理想;p-q法受电网谐波和不对称的影响很大,补偿效果很差。
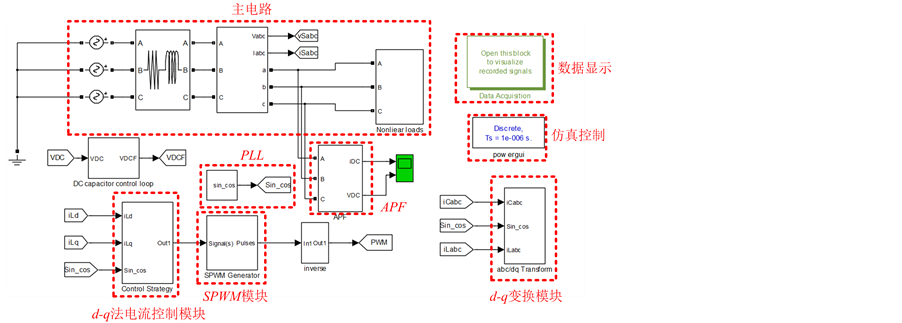
Figure 3. Simulation model of d-q method
图3. d-q法仿真模型
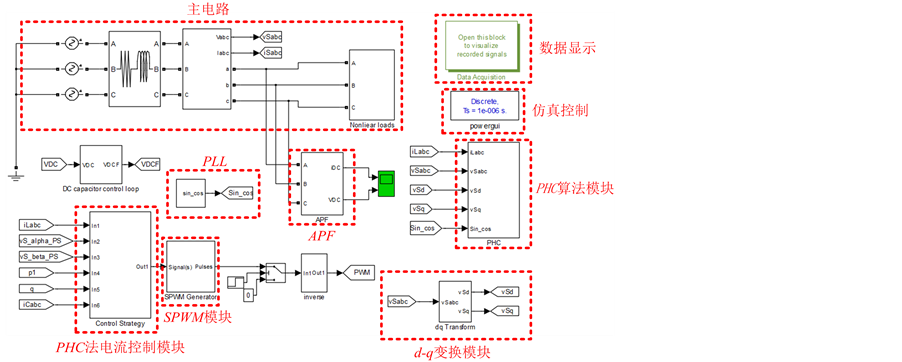
Figure 4. Simulation model of PHC method
图4. PHC法仿真模型
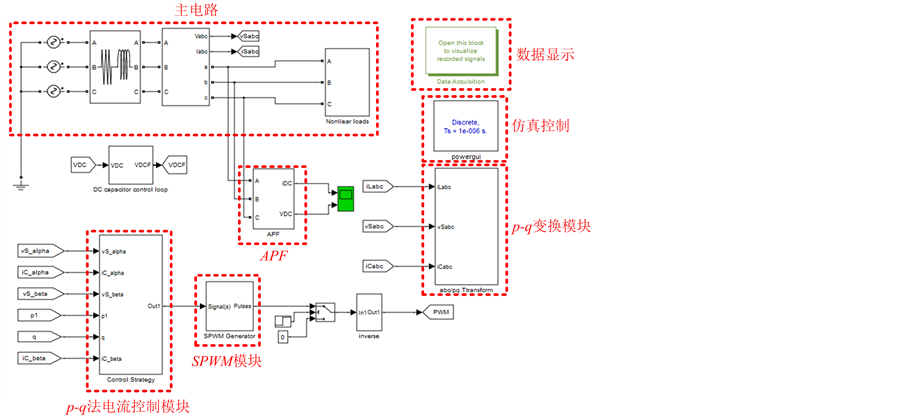
Figure 5. Simulation model of p-q method
图5. p-q法仿真模型
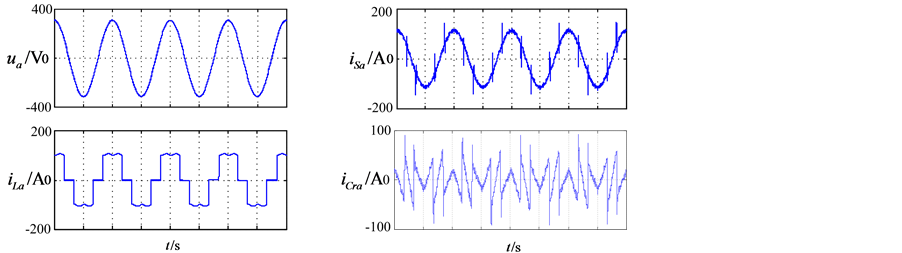 (a) 补偿前的仿真波形 (b) d-q法的仿真波形
(a) 补偿前的仿真波形 (b) d-q法的仿真波形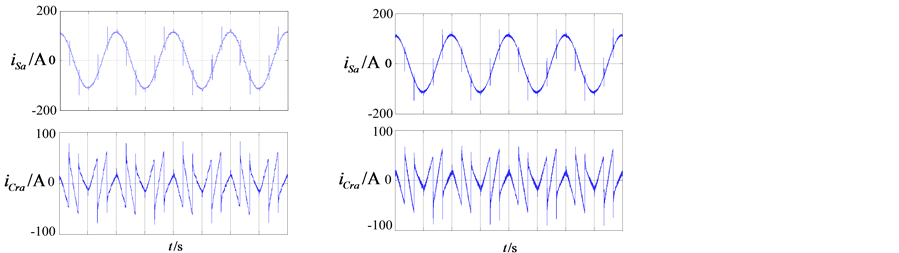 (c) PHC法的仿真波形 (d) p-q法的仿真波形
(c) PHC法的仿真波形 (d) p-q法的仿真波形
Figure 6. Simulation waveforms of the three methods using sinusoidal symmetry voltage
图6. 电网电压正弦对称条件下的三种算法仿真波形图
 (a) 补偿前的仿真波形 (b) d-q法的仿真波形
(a) 补偿前的仿真波形 (b) d-q法的仿真波形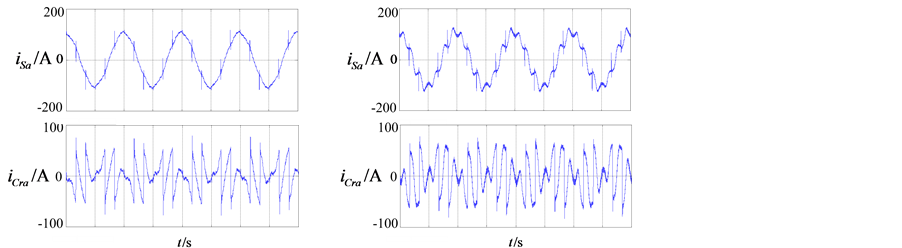 (c) PHC法的仿真波形(d) p-q法的仿真波形
(c) PHC法的仿真波形(d) p-q法的仿真波形
Figure 7. Simulation waveforms of the three methods using non-sinusoidal symmetry voltage
图7. 电网电压含谐波条件下的三种算法仿真波形图
 (a) 补偿前的仿真波形 (b) d-q法的仿真波形
(a) 补偿前的仿真波形 (b) d-q法的仿真波形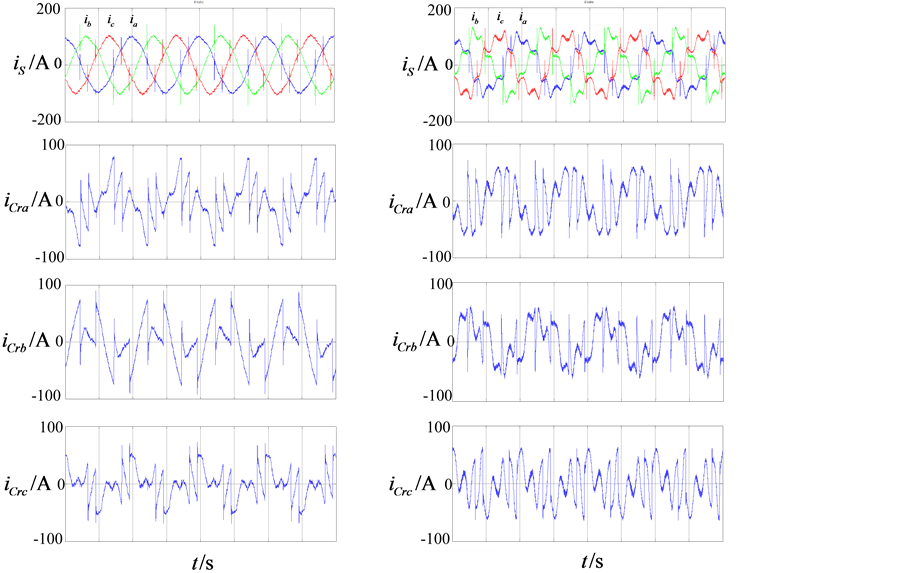 (c) PHC法的仿真波形 (d) p-q法的仿真波形
(c) PHC法的仿真波形 (d) p-q法的仿真波形
Figure 8. Simulation waveforms of the three methods using non-sinusoidal dissymmetry voltage
图8. 电网电压含谐波不对称条件下的三种算法仿真波形图
4. 结论
从以上仿真波形和结果可以看出,当电网电压对称正弦时,三种谐波电流检测方法均可以准确有效地检测出负载电流中所含的谐波电流分量。当电网电压出现非正弦或不对称时,d-q法和PHC法都有一定的补偿效果,由于PHC法考虑电源电压的基波正序分量,因而可以充分补偿掉谐波分量以及部分不对称分量,因此PHC法效果更好。综上所述,在三相非正弦不对称系统的应用场合,PHC法的补偿效果要好于d-q法和p-q法。
文章引用
孔 昕,王宝华. APF中完美谐波消除法的仿真与分析
Simulation and Analysis of the Perfect Harmonic Cancellation Method for APF[J]. 智能电网, 2015, 05(06): 285-292. http://dx.doi.org/10.12677/SG.2015.56034
参考文献 (References)
- 1. 姚杰. 并联型有源电力滤波器的控制算法研究[D]: [硕士学位论文]. 武汉: 华中科技大学, 2009.
- 2. Grady, W.M., Samotyi, M.J. and Noyola, A.H. (1990) Survey of Active Power Line Conditioning Methodologies. IEEE Transactions on PD, 5, 1536-1542. http://dx.doi.org/10.1109/61.57998
- 3. 丁道宏. 电力电子技术[M]. 修订版. 北京: 航空工业出版社, 1999.
- 4. 陈东华. 有源滤波应用于飞机交流电源系统的关键技术研究[D]: [博士学位论文]. 南京: 南京航空航天大学, 2007.
- 5. 石磊. 新型航空并联有源电力滤波器的研究[D]: [硕士学位论文]. 南京: 南京航空航天大学, 2011.
- 6. 李建林, 张仲超. 有源电力滤波器控制策略综述[J]. 电力建设, 2003, 24(6): 44-46.
- 7. 王兆安, 杨君, 等. 谐波抑制和无功功率补偿[M]. 北京: 机械工业出版社, 2005: 220-241.
- 8. Akagi, H., Fujita, H. and Wada, K. (1999) A Shunt Active Filter Based on Voltage Detection for Harmonic Termination of a Radial Power Distribution Line. IEEE Transactions on IA, 35, 638-645. http://dx.doi.org/10.1109/28.767015
- 9. 魏志强. 电力有源滤波器谐波检测方法研究[D]: [硕士学位论文]. 天津: 天津大学, 2007.
- 10. Akagi, H., Kanazava, Y. and Nabae, A. (1984) Instantaneous Reactive Power Compensators Comprising Switching Devices without Energy Storage Component. IEEE Transactions and APPI, 20, 625-630. http://dx.doi.org/10.1109/TIA.1984.4504460
- 11. Montero, M., Cadaval, E. and Gonzalez, F. (2007) Comparison of Control Strategies for Shunt Active Power Filters in Three-Phase Four-Wire System. IEEE Transactions on Power Electronics, 22, 229-236. http://dx.doi.org/10.1109/TPEL.2006.886616
- 12. Rafiei, M.R., Toliyat, H.A., Ghazi, R. and Gopalarathanam, T. (2001) An Optimal and Flexible Control Strategy for Active Filtering and Power Factor Correction under Nonsinusoidal Line Voltages. IEEE Transactions on Power Delivery, 16, 297-305. http://dx.doi.org/10.1109/61.915499
- 13. 卢盈. 应用于飞机交流电源的有源电力滤波器研究[D]: [硕士学位论文]. 南京: 南京航空航天大学, 2009.