Operations Research and Fuzziology
Vol.07 No.01(2017), Article ID:19807,9
pages
10.12677/ORF.2017.71003
An Algorithm to Select Satisfying Alternative for Fuzzy Multiple Attribute Decision Making Problem
Yingying Jiang
School of Mathematics, Yunnan Normal University, Kunming Yunnan

Received: Feb. 7th, 2017; accepted: Feb. 21st, 2017; published: Feb. 24th, 2017

ABSTRACT
In this paper, the decision programming with L-R fuzzy number changed into common decision programming by sorting rule. A multi-attribute decision algorithm is presented to help decision- maker find the best alternative from alternatives set based on nonlinear utility function and outranking relation.
Keywords:Sorting Rule, L-R Fuzzy Number, Nonlinear Utility Function
一种模糊多属性决策选优算法
蒋莹莹
云南师范大学,数学学院,云南 昆明
收稿日期:2017年2月7日;录用日期:2017年2月21日;发布日期:2017年2月24日

摘 要
在属性指标值为L-R模糊数情况下,利用排序准则将含有模糊数的决策规划模型转换成普通决策规划模型。基于非线性效用函数与级别优于关系相结合的方法提出一种多属性决策算法帮助决策者对方案集中方案进行选优。
关键词 :排序准则,L-R模糊数,非线性效用函数

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
多准则决策大体分三类:基于效用函数,基于级别优于关系和基于距离。文献 [1] [2] 是利用各种形式的效用函数研究方案评价问题,绝大部分的文献所用的都是简单的线性效用函数。由于人类知识结构的不完备及对客观事物的认知具有较大的主观性,而实际的决策中经常出现决策信息的模糊性和不确定性。目前不确定性区间数 [3] [4] 、三角模糊数 [5] [6] 的多属性决策问题多有研究其中文献 [4] 给出了误差分析法 [4] 文献 [3] 提出了线性规划法。而本文决策模型的目标函数选用的是非线性的效用函数并且以L-R模糊数来表示模糊抽象的属性指标值。运用模糊理论 [6] 结合Adamo、Yager [7] 和张曾科等其他学者的模糊数排序准则提出一种新的排序准则将模糊规划转化为普通规划,简化决策规划使算法更具合理性。把模糊理论与多属性决策相结合在模糊环境下寻求更为有效的转化方法来帮助决策者对方案集中方案进行选优。
2. 备用知识
2.1. 偏好于效用函数
定义2.1.1:严格序 [8] “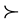 ”:
”: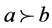 (或记作
(或记作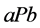 )的含义是“a优于b”(a is preferred to b);
)的含义是“a优于b”(a is preferred to b);
定义2.1.2:无差异 [8] “~”: (或记作
(或记作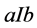 )的含义是“a无差异于b”(a is indifference to b);决策人对选择a或b同样满意。
)的含义是“a无差异于b”(a is indifference to b);决策人对选择a或b同样满意。
定义2.1.3:弱序 [8] “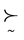 ”:
”: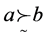 (或记作
(或记作 )的含义是“a补劣于b”,即a优于或无差异于b。
)的含义是“a补劣于b”,即a优于或无差异于b。
定义2.1.4 [8] :在集合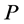 上的实值函数
上的实值函数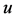 ,若它和
,若它和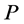 上的优先关系
上的优先关系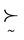 一致,即若
一致,即若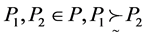 当且仅当
当且仅当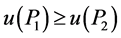 。则称
。则称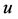 为效用函数。
为效用函数。
(对于完全明确的偏好,若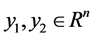 为两个决策方案,
为两个决策方案, 为一效用函数,则有
为一效用函数,则有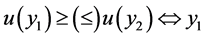 优于或无差异于 [8] (劣于或无差异于)
优于或无差异于 [8] (劣于或无差异于) 。)
。)
2.2. 隶属度
定义2.2.1 [6] :论域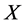 到[0,1]闭区间上的任意映射
到[0,1]闭区间上的任意映射
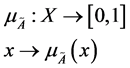
都确定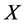 上的一个模糊集
上的一个模糊集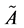 ,
,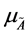 叫做
叫做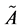 的隶属函数 [6] ,
的隶属函数 [6] ,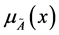 叫做
叫做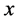 对
对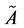 的隶属度,记为
的隶属度,记为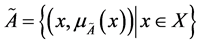 。显然,模糊
。显然,模糊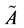 完全由隶属函数
完全由隶属函数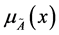 画,当
画,当 时,
时, 退化为
退化为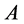 ,
,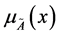 退化为特征函数
退化为特征函数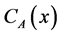 。
。
2.3. L-R模糊数
定义2.3.1 [6] :设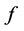 是实数域
是实数域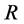 到
到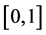 区间的映射
区间的映射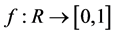 ,如果
,如果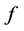 满足以下条件:
满足以下条件:
(1)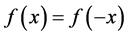 ,
,
(2)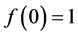 ,
,
(3)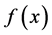 在区间
在区间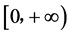 单调递减,则称
单调递减,则称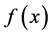 为模糊数的基准函数。
为模糊数的基准函数。
定义2.3.2 [6] :设 分别为模糊数
分别为模糊数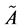 的左右基准函数,如果
的左右基准函数,如果
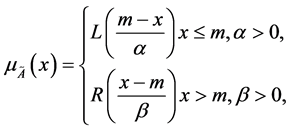
则称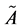 为L-R模糊数,记为
为L-R模糊数,记为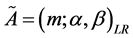 ,其中
,其中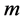 称为
称为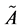 的均值,
的均值, 称为
称为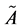 的左、右扩散。当
的左、右扩散。当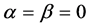 时,L-R模糊数退化为一般的实数,即
时,L-R模糊数退化为一般的实数,即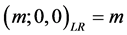 。
。
L-R模糊数运算法则:
定理2.3.1:设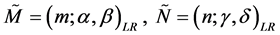 则:
则:
(1)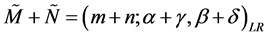 ,
,
(2)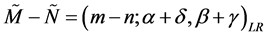 。
。
2.4. 不同类型属性指标值归一化
(1) 收益类模糊指标值的归一化
设有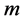 个模糊指标值
个模糊指标值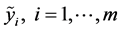 。令
。令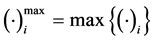 。如果
。如果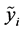 是L-R模糊数,记为
是L-R模糊数,记为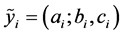 。
。 分别为
分别为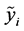 的左右边界值;则归一化 [6] 的模糊指标值
的左右边界值;则归一化 [6] 的模糊指标值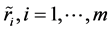 可写为
可写为
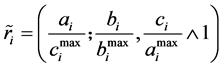 。
。
(2) 成本类模糊指标值的归一化
设有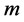 个模糊指标值
个模糊指标值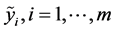 。令
。令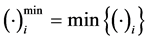 。如果
。如果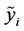 是L-R模糊数,记为
是L-R模糊数,记为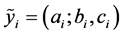 .
.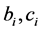 分别为
分别为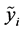 的左右边界值;则归一化的模糊指标值
的左右边界值;则归一化的模糊指标值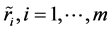 可写为
可写为
 。
。
3. 问题描述与算法
有限方案集合为 ;
;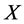 是方案
是方案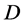 的一组属性指标集,
的一组属性指标集,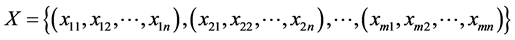 。在属性指标值模糊的情况下,候选方案
。在属性指标值模糊的情况下,候选方案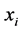 的第
的第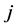 个指标若用L-R模糊数
个指标若用L-R模糊数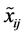 表示,则用L-R模糊数矩阵来表示模糊多属性决策问题,如下形式:
表示,则用L-R模糊数矩阵来表示模糊多属性决策问题,如下形式:
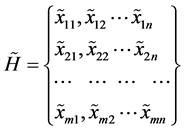
其中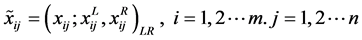 。是由
。是由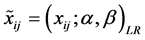 ,转化的L-R模糊数;
,转化的L-R模糊数;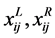 分别是
分别是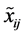 的左、右边界值。
的左、右边界值。
决策者所用的决策模型中的效用函数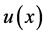 是非线性的 [9] ,即
是非线性的 [9] ,即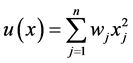 ,
,
其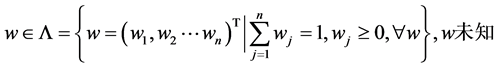 。
。
用来分析判断比较方案间关系的规划其属性指标值若为L-R模糊数。则规划转换如下:
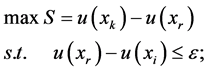 (1)
(1)
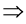
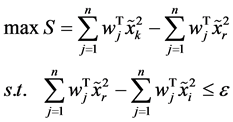 (2)
(2)
和
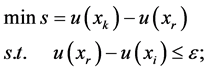 (3)
(3)
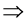
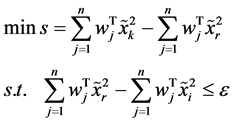 (4)
(4)
其中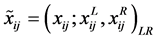 是L-R模糊数,
是L-R模糊数,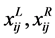 分别是
分别是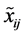 的左、右边界值,而不是左右扩散;则
的左、右边界值,而不是左右扩散;则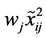 也是L-R模糊数,记为
也是L-R模糊数,记为
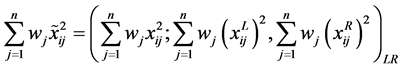
且有:
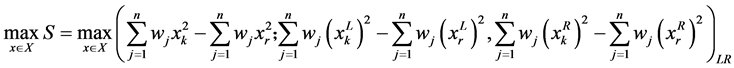 。
。
基于对L-R模糊数排序,张曾科(1977)提出了判断准则:设 ,
,
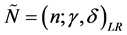 则:
则:
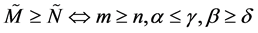 。
。
为避免规划转换的结果不好,现对此准则进行改进得到新的排序准则:
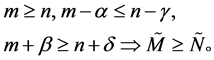
则规划(3)、(4)转化成如下:
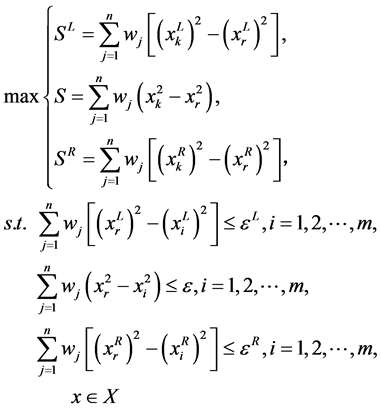 (5)
(5)
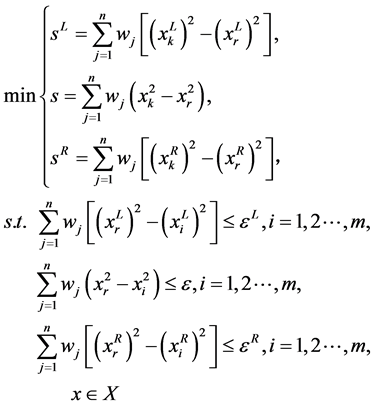 (6)
(6)
此时规划由含有模糊数的规划转化成非模糊的多目标决策规划,利用经典的多目标线性规划方法求解。
由于目标之间的相互制约与矛盾,一般最优解在多目标决策问题中是不存在的。决策者必须通过其他的方法来进行求解。本文采用的是加权的方法将多目标的决策规划转化成单一目标可进行求解的决策规划。
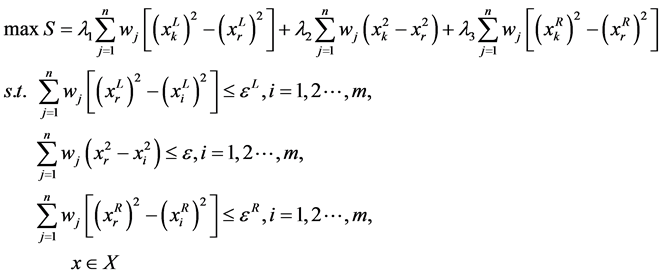 (7)
(7)
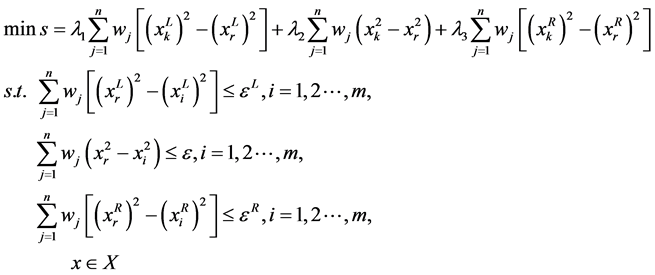 (8)
(8)
其中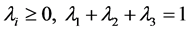 。
。
决策者可根据属性的重要程度赋予不同权重。但本文为了讨论及计算的简便把每个目标的权重看作同等重要,取 。
。
若解规划(7)得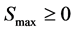 ,即
,即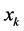 优于或无差异于
优于或无差异于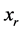 ,将
,将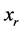 从
从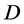 中删除,同时生成约束条件
中删除,同时生成约束条件 ,
, 和
和 。将其加入到规划(7),(8)的约束中;若最优值
。将其加入到规划(7),(8)的约束中;若最优值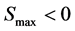 ,在求解规划(8)若其最优值
,在求解规划(8)若其最优值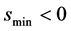 。
。
即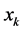 优于或无差异于
优于或无差异于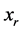 ,互换
,互换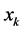 与
与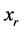 的值,将
的值,将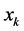 从
从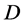 中删除并生成约束条件
中删除并生成约束条件
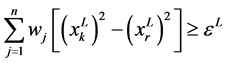 ,
,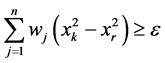 和
和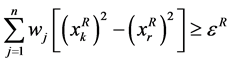 。将其加入到规划(7),(8)的约束中,然后用新的
。将其加入到规划(7),(8)的约束中,然后用新的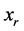 替换规划(7),(8)约束中的
替换规划(7),(8)约束中的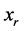 ;否则保留
;否则保留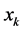 。
。
用此方法依次处理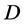 中的其他方案,具体实施步骤如下:
中的其他方案,具体实施步骤如下:
步骤一:任意的选取一组权系数,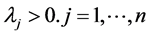 (一般为了便于计算,令
(一般为了便于计算,令 )。从
)。从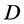 中找出一个能令
中找出一个能令 取值最大的,则此方案即为初始满意方案,记作
取值最大的,则此方案即为初始满意方案,记作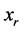 ,令
,令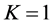 ;
;
步骤二:任取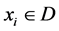 ,将
,将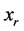 与
与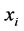 交给决策者进行判断,若结果为
交给决策者进行判断,若结果为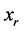 优于或无差异于
优于或无差异于 ,转至步骤三,如果比较的结果为
,转至步骤三,如果比较的结果为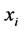 优于或无差异于
优于或无差异于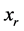 ,转至步骤四。
,转至步骤四。
步骤三:将 从
从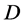 中删除,得到约束条件
中删除,得到约束条件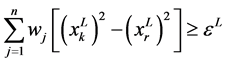 ,
, 和
和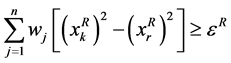 ,如果
,如果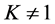 ,那么将此约束加入规划(7)、(8)的约束中,再转至步骤五。
,那么将此约束加入规划(7)、(8)的约束中,再转至步骤五。
步骤四:交换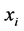 与
与 的值,将
的值,将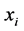 从
从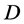 中删除,并得到约束条件
中删除,并得到约束条件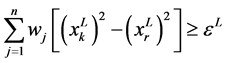 ,
,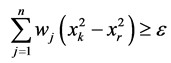 和
和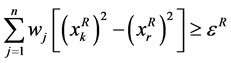 如果
如果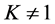 ,那么将此约束加入到规划(7)、(8)的约束中,并以新的
,那么将此约束加入到规划(7)、(8)的约束中,并以新的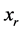 将此约束中原来的
将此约束中原来的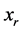 替换掉。
替换掉。
步骤五:任意选取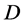 中方案
中方案 ,解规划(7),若(7)的
,解规划(7),若(7)的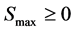 ,那么将
,那么将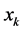 与
与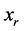 的值互换,并将
的值互换,并将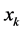 从
从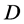 中删除,并把
中删除,并把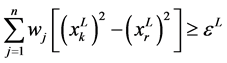 ,
,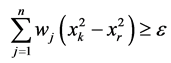 和
和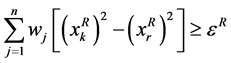 加入规划(7),(8)的约束中然后用新的
加入规划(7),(8)的约束中然后用新的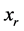 将规划(7),(8)约束中旧的
将规划(7),(8)约束中旧的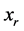 替换掉;如果规划(7)的
替换掉;如果规划(7)的 ,再求解规划(8),若其最优值
,再求解规划(8),若其最优值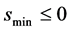 ,那么将
,那么将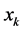 从
从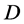 中删除,与此同时生成约束条件
中删除,与此同时生成约束条件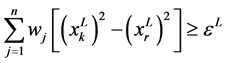 ,
,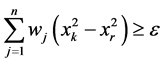 和
和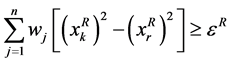 并将此约束加入到(7),(8)的约束中;否则保留
并将此约束加入到(7),(8)的约束中;否则保留 。按此步骤,判断
。按此步骤,判断 中剩余方案,并将保留下来的方案仍记作
中剩余方案,并将保留下来的方案仍记作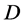 。
。
步骤六:如果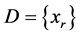 ,则
,则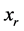 为决策者满意的方案,停止;否则令
为决策者满意的方案,停止;否则令 ,返回步骤二。
,返回步骤二。
4. 算例
为了解学生的身体素质情况对云南师范大学本科学生体育锻炼等级以问卷的形式做详细调查,主要是锻炼行为及归因方式、心境的调查。对学生锻炼情况从外部身体的体能锻炼到内部心境的综合评定判断其等级情况。其中心境量表主要从紧张、愤怒、疲劳、抑郁、精力、慌乱、自尊这七个方面进行考量,现从统计表中抽取部分同学的心境指标值进行心境程度的选优。
现从众多问卷表中抽四人进行心境模拟选优。用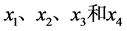 分别代表依次抽到的四位同学。方案集
分别代表依次抽到的四位同学。方案集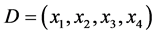 ,用
,用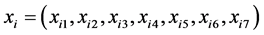 表示第
表示第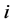 位同学心境的七个属性的指标值。其中紧张、愤怒、疲劳、抑郁、慌乱属于成本类指标,精力和自尊属于收益类指标。由于问卷调查的调查项具有模糊性所以属性指标值用L-R模糊数表示,这四位同学的模糊属性值矩阵如下
位同学心境的七个属性的指标值。其中紧张、愤怒、疲劳、抑郁、慌乱属于成本类指标,精力和自尊属于收益类指标。由于问卷调查的调查项具有模糊性所以属性指标值用L-R模糊数表示,这四位同学的模糊属性值矩阵如下
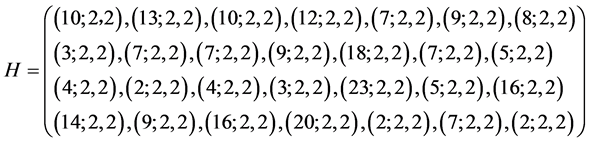 。
。
为便于指标间的比较现把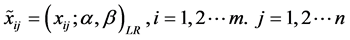 带扩散型的L-R模糊数转化成含边界值的模糊数,如下形式:
带扩散型的L-R模糊数转化成含边界值的模糊数,如下形式:
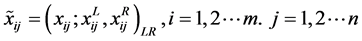 。
。
则上述矩阵变为:
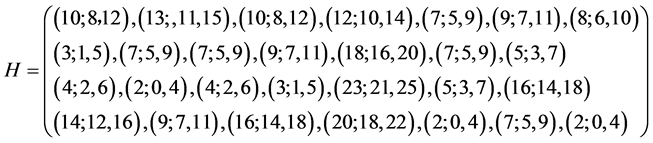 。
。
由于指标的类型不同不便于直接应用决策模型,所以要用备用知识中的2.4不同类型指标值的归一化方法进行归一化处理,处理如下:
 。
。
由决策者的方法取 为初始参照方案,取
为初始参照方案,取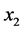 与
与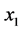 由决策者判断,有
由决策者判断,有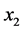 优于
优于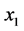 ,把
,把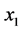 从
从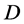 中删除,同时生成约束条件
中删除,同时生成约束条件
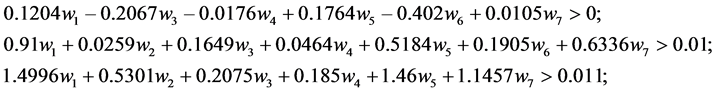
对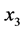 用下面规划进行抉择:
用下面规划进行抉择:
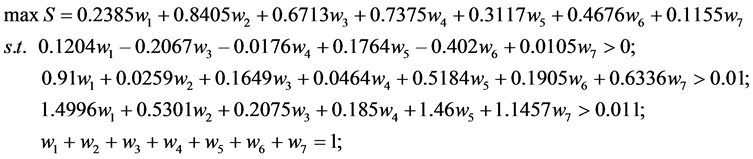 (9)
(9)
得 。则
。则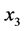 优于
优于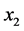 ,则把
,则把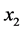 从中删除,生成约束条件
从中删除,生成约束条件
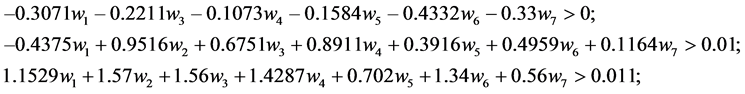
并把此约束加入到规划(9)中。
对于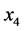 则参考如下规划:
则参考如下规划:
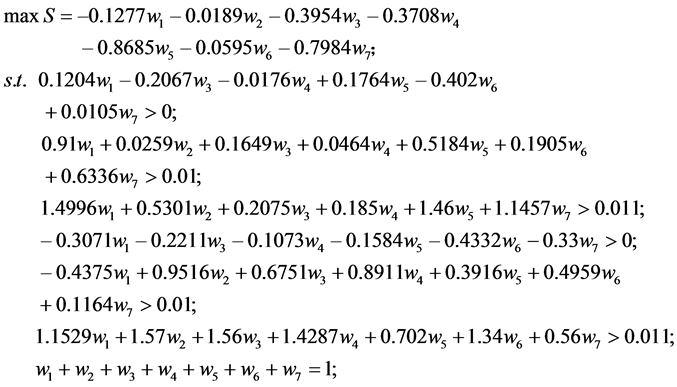 (10)
(10)
解得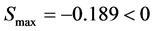 ,在规划(10)的约束下求解:
,在规划(10)的约束下求解:

解得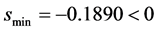 ,即
,即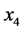 劣于
劣于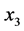 ,把
,把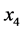 从
从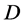 中删除。最后
中删除。最后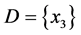 ,即
,即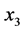 为决策者的最佳方案。
为决策者的最佳方案。
5. 结论
本文提出一种基于非线性效用函数与级别优于关系相结合在L-R模糊数情况下多属性决策选优算法。用模糊数排序准则及模糊理论将复杂的模糊数近似的处理成简单的精确数,简化了决策规划的处理步骤使得算法更为合理有效。最后通过实际例子验证算法的合理性与有效性。
基金项目
云南省自然科学基金(No. 2013FB034)。
文章引用
蒋莹莹. 一种模糊多属性决策选优算法
An Algorithm to Select Satisfying Alternative for Fuzzy Multiple Attribute Decision Making Problem[J]. 运筹与模糊学, 2017, 07(01): 22-30. http://dx.doi.org/10.12677/ORF.2017.71003
参考文献 (References)
- 1. Bous, G., Fortemps, P., Glineur, F., et al. (2010) ACUTA: A Novel Method for Additive Function on Basis of Holistic Preference Statements. European Journal of Operational Research, 206, 435-444. https://doi.org/10.1016/j.ejor.2010.03.009
- 2. Angilella, S., Creco, S. and Matarazzo, B. (2010) Non-Additive Robust Ordinal Regression: A Multiple Criteria Decision Model Based on the Choquet Integra. European Journal of Operational Research, 201, 277-288. https://doi.org/10.1016/j.ejor.2009.02.023
- 3. Yoon, K. (1989) Propagation of Errors in Multiple Attribute Decision Analysis: A Practical Approach. Journal of the Operation Research Society, 40, 681-686. https://doi.org/10.1057/jors.1989.111
- 4. 樊治平, 郭亚军. 误差分析理论在区间数多属性决策问题中的应用[J]. 东北大学学报, 1997, 18(5): 550-560.
- 5. 徐泽水. 不确定多属性决策方法及应用[M]. 北京: 清华大学出版社, 2004.
- 6. 李荣均. 模糊多准则决策理论与应用[M]. 北京: 科学出版社, 2002.
- 7. Yager, R.R. (1988) On Ordered Weighted Averaging Aggregation Operators in Multi-Criteria Decision Making. IEEE Transactions on Systems, Man and Cybemeties, 18, 183-190. https://doi.org/10.1109/21.87068
- 8. 岳超源. 决策理论与方法[M]. 北京: 科学出版社, 2013.
- 9. Chankong, V. and Haimes, Y.Y. (1983) Multiobjective Decision Making: Theory and Methodology. Series Volume 8, Elsevier Science Publishing Co., New York, Amsterdam, Oxford, 67-85.