Operations Research and Fuzziology
Vol.
13
No.
06
(
2023
), Article ID:
76356
,
13
pages
10.12677/ORF.2023.136594
基于改进的傅里叶神经算子数值求解频率域声波方程
潘代英,何清龙
贵州大学,数学与统计学院,贵州 贵阳
收稿日期:2023年8月31日;录用日期:2023年11月22日;发布日期:2023年11月29日

摘要
在许多应用中,频率域声波方程的数值求解发挥着重要作用,如医学成像和地震勘探。传统的频率域声波方程求解方法,如有限差分法、有限元法等,通常具有参数依赖性,导致计算成本高昂。本文提出了一种结合残差网络(ResNet)和傅里叶神经算子(FNO)的神经网络方法(RFNO),以快速求解频域声波方程。RFNO可以学习从速度参数函数空间到波场函数空间的映射。因此,当神经网络经过适当训练后,对于不同的速度可以快速高效给出波动方程的近似解。基于简单分层模型和Marmousi模型数据集进行的数值实验,以验证RFNO的有效性。数值结果表明,RFNO在计算效率方面表现出良好的性能。因此,在反问题求解过程中,RFNO是非常具有竞争力的一种正问题求解器。
关键词
频率域声波方程,傅里叶神经算子,函数空间,Marmousi模型

Numerical Solution of Frequency-Domain Acoustic Wave Equation Based on Improved Fourier Neural Operator
Daiying Pan, Qinglong He
School of Mathematics and Statistics, Guizhou University, Guiyang Guizhou
Received: Aug. 31st, 2023; accepted: Nov. 22nd, 2023; published: Nov. 29th, 2023

ABSTRACT
Frequency-domain numerical solutions of acoustic wave equation play an essential role in many applications, such as the medical imaging, and seismic exploriation. Traditional methods for solving the frequency-domain acoustic wave equation, such as the finite-difference method, the finite-element method and so on, usually are parametric dependence, resulting in high computational cost. In this study, we propose a neural network method that combines the residual networks (ResNet) and Fourier neural operators (FNO) to solve the acoustic wave equation in the frequency domain (RFNO). RFNO can learn the mapping from the velocity parametric function space to the wavefield function space. Therefore, it is very efficient to give the approximate solution for different velocities when the neural network is properly trained. Numerical experiments based on the simple layered model and Marmousi model, are presented. The numerical results show that the RFNO has a good performance in solving acoustic wave equation in terms of the computational efficiency. It thus may be a competitive forward problem solver for the inverse problems.
Keywords:Frequency-Domain Acoustic Wave Equation, Fourier Neural Operators, Function Space, Marmousi Model

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
频率域声波方程的数值求解在许多科学问题中扮演着重要角色,如医学成像、无损检测和地震勘探等等 [1] [2] 。对于这些问题,通常无法得到声波方程的解析解,因此需要使用数值方法进行求解。此外,这类问题往往需要声波方程针对不同的参数模型(如速度、密度)进行多次求解,导致了计算成本大大增加。
有限差分法(FDM)和有限元法(FEM)是求解声波方程的两种主要数值方法 [3] [4] 。这些方法首先对声波方程进行离散化处理,并得到一个依赖于模型参数的线性方程组。然后,通过数值求解这个线性方程组,得到方程的一个近似解。因此,对于不同的模型参数,需要进行独立的有限差分法或有限元法求解,传统数值方法的模型依赖特性极大地限制了其在科学计算问题中的广泛应用。
随着计算能力的提升和神经网络的改进,基于神经网络的深度学习方法在图像处理、语音识别、自然语言处理等许多领域取得了不错的成果 [5] [6] [7] 。根据通用逼近定理,神经网络不仅可以逼近任何Borel可测函数,还可以以预先给定的精度逼近两个有限维空间之间的映射关系 [8] 。此外,神经网络还具拟合从一个函数空间到另一个函数空间的映射的巨大潜力。最近,深度学习方法在基于偏微分方程的正反问题求解中引起了广泛关注 [9] 。
在求解偏微分方程问题中,深度学习方法可以分为两类。第一类方法是有限维算子方法,它将解算子参数化为在有限维欧氏空间中的深度神经网络 [10] [11] 。因此,这些有限维算子方法依赖于网格,并需要针对不同的分辨率和离散化进行网络参数修改和调整,以达到的满足所给的误差水平。换句话说,这些方法具有网络依赖性。另一种方法是基于物理信息的深度学习方法,该类方法将神经网络与物理定律结合,因此具有处理非线性、高维和更复杂的偏微分方程的能力 [12] 。然而,物理信息学习方法的局限性在于,任何物理属性的变化都需要独立进行训练。类似于传统的解法方法,物理信息学习方法的缺点是需要针对新的物理属性重新训练神经网络,这极大地增加了计算成本。
深度神经算子学习可以学习无穷维函数空间之间的映射关系,在处理高维问题方面起着重要作用 [13] 。深度神经算子的最显著优势之一是它是一种免网格方法(grids free),因此可以极大地降低计算成本,并可应用于快速求解反问题 [14] [15] [16] 。傅里叶神经算子(Fourier Neural Operator, FNO)是一种强大的求解偏微分方程和其他数学问题的神经算子方法,它从有限观测的输入与输出对中学习了两个无穷维空间之间的映射关系。RNO学习框架的主要思想是将输入数据转换为频域表示,这使得更好地理解和提取受偏微分方程约束的解算子的内在结构特征 [17] [18] 。傅里叶神经算子广泛用于数值求解涉及偏微分方程的许多问题 [19] [20] [21] 。增强型傅里叶神经算子是傅里叶神经算子的一种推广(UFNO),它用于求解多孔介质中地质碳封存模拟问题 [22] 。傅里叶神经算子还被用于求解具有多个源和频率的地震波方程 [23] [24] 。
本研究主要考虑利用傅里叶神经算子求解多个速度模型、震源和频率的频域声波方程问题。为了提高傅里叶神经网络的泛化能力,本文引入了残差模块,提出了深度残差傅里叶神经算子(RFNO)。RFNO可以减弱误差反向传播过程中梯度消失挑战,从而提高训练的计算效率。此外,不同网络层次之间的残差连接使得RFNO能够有效利用不同层次特征的互补性,从而提高神经网络的泛化能力。基于简单分层模型和Marmousi模型的数值实验,验证了所提出的深度神经方法在重复求解不同物性参数的波动方程上的有效性。
2. 频率域声波方程
声波方程描述了振动在声学介质中的传播规律。时间域和频率域声波方程在许多科学和工程问题中起着重要作用。本研究仅关注频域中的声波方程。在各向同性和非均匀声学介质中,具有恒定密度的二维频域声波方程即为著名的亥姆霍兹方程(Helmholtz equation):
(1)
其中, 表示压力波场, 代表角频率, 表示介质中的波传播速度, 是小波函数, 是有界的开集, 是狄拉克函数。声波方程(1)的解可以形式上写为:
(2)
可以被视为从 到解空间的非线性算子。
3. 改进的傅里叶神经算子
考虑基于傅里叶神经算子对非线性算子 进行近似。为此,设 为 组成的函数空间,假设 为声波方程解的函数空间。因此,非线性算子是一个映射: 。
FNO是一种被广泛应用和研究的神经算子方法之一。FNO采用全连接神经网络将输入 映射到更高维空间中的表示 , 称为初始状态。然后,进行迭代更新T,即 ,再使用另一个全连接神经网络将最后的状态 转化为低维空间 中作为RNO的最终输出。在迭代更新过程中,每一次更新定义为:
(3)
其中,W是一个线性变换(例如,全连接网络、卷积网络), 是一个逐元素作用的非线性激活函数,用于增加神经网络的表示能力,K表示由 参数化的有界线性算子,通常定义为:
(4)
在公式(3)和(4)中,W和 都构成了FNO的可学习参数。
Table 1. Detailed input and output dimensions of the RFNO architecture
表1. RFNO架构的详细输入和输出维度

Figure 1. The architecture of RFNO, where li denotes the Fourier layer and ki denotes the R-Fourier layer.
图1. RFNO的架构RFNO的架构:li为傅里叶层,ki为R-Fourier层
为了加速公式(4)的积分过程,一个合理的核函数的选择是 ,该选择从基本解的角度来看是一个自然的选择,于是公式(4)因此成为了一个被广泛熟知的卷积算子:
(5)
通过应用卷积定理,可以利用傅里叶变换高效地计算公式(5),即
(6)
其中 表示傅里叶变换, 表示逆傅里叶变换。值得注意的是,公式(6)可以通过使用快速傅里叶变换来进行高效计算。为了增强FNO对偏微分方程算子的表示能力,并缓解训练过程中梯度消失的难题,在傅里叶层中的引入残差网络。图1展示了本文的神经网络架构,本文将其称为RFNO。在图1中,RES代表残差网络。RFNO由传统的傅里叶层和RES层交替组成,共有34层,具体的RFNO网络结构如表1所示。RFNO的优势在于傅里叶层将数据集变换到傅里叶域(频率特性),以及残差网络合理运用不同层之间的特征信息。
4. 数值实验
在本节中,主要关注基于二维频域声波方程的RFNO的数值性能。RFNO的输入包括速度、频率和震源位置信息。标签是基于传统高阶有限差分方法得到的声波方程数值解,对应于给定的速度、频率和震源。因此,数据集表示为 ,其中 是 网格上的速度模型, 表示频率信息(考虑频率的幅度, 范围为3到15 Hz), 表示源位置信息, 表示计算域的离散化, 表示频域压力波场的实部, 表示频域压力波场的虚部。当数据输入RFNO时,输入数据有五个通道,第一个通道是速度分布,第四个和五个通道是计算域的离散化,即 。需要注意的是,第二个通道表示频率信息,第三个通道表示震源位置。根据这些输入数据,RFNO的输出数据包含两个通道。其中一个通道是波场的实部,另一个通道是波场的虚部。
本文的数值模拟实验在GPU (GeForce GTX 1080 VTi)上进行。RFNO是基于PyTorch深度学习框架实现。激活函数为GELU函数,损失函数定义为 范数。在训练过程中,使用的优化求解器为 Adam,初始学习率设置为 ,总的训练时间约为1.2小时。
4.1. 简单分层模型
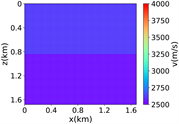
为了评估所提出方法的数值性能,先使用一个简单的数据集来训练RFNO,该数据集仅包含简单的分层模型。数据集包含1000个样本数据,其包括均质速度模型、双层速度模型和四层速度模型。每个模型维度大小为84 × 84,并且 ,速度范围为2500 m/s至4000 m/s。图2中的(i)展示了数据集中的部分简单模型。在这个实验中,使用900个速度模型进行训练,100个速度模型进行测试。RFNO进行了100个epoch的训练,批量大小为20。在训练过程中,使用12个傅立叶模式,傅立叶层的宽度设置为32。
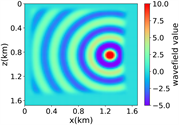
图2中的(ii)到(vi)展示了分层模型下的不同物性参数的波场模拟结果,首先图(ii)为单源单频时RFNO进行的数值性能测试,在这个实验中,频率为8.25 Hz,源位于计算域的中心位置,再结合图(vi)中训练集每次训练迭代的相应损失函数的变化,结果表明RFNO模拟波场结果与实际波场值非常接近,成功地捕捉了波场的细节。其次,在多源单频的情况下,选取5个源的位置:(0.42 km,0.84 km)、(0.84 km,0.42 km)、(0.84 km,0.84 km)、(0.84 km,1.26 km)和(1.26 km,0.84 km),频率为8.25 Hz。图(iii)为RFNO计算的数值结果,从图中可以看出对于简单分层模型下,RFNO的结果还是比较理想的。针对单源多频模拟问题,图(iv)所示单源多频结果,从图中以及结合表2可以得出,随着频率的升高RFNO的模拟精度逐渐降低。最后,在多源多频率的图(v)情况下,低频的训练集和验证集波场模拟结果是非常好,但对于测试集是高频的波场模拟总体效果不错。
(a)(b) (c)
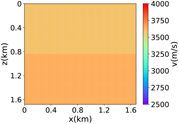

(d) (e) (f)
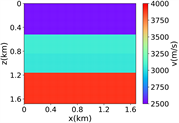
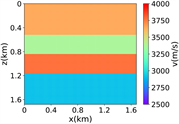

(g)(h) (i)
(i) 简单分层模型
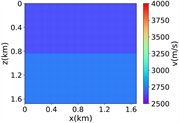
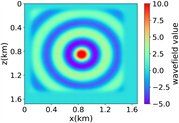
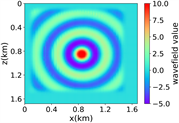
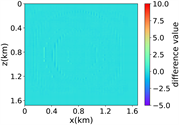
(a)(b) (c) (d)
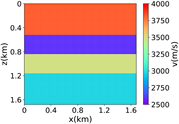
(e)(f) (g) (h)
(i)(j) (k) (l)
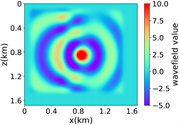
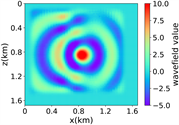
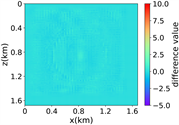
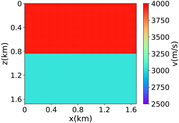
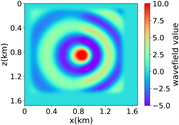
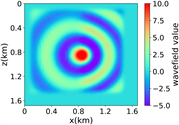
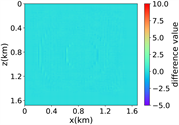
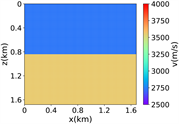
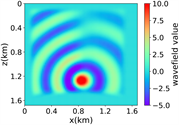
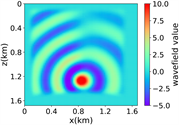
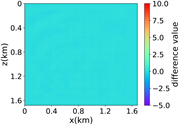
(ii) 简单分层模型下单频单源对应的波场图,震源位置为(0.84 km,0.84 km),频率为8.25 Hz
注:第一行为训练集,第二行为验证集,第三行为测试集;第一列为速度模型,第二列为实际波场,第三列为RFNO模拟的波场,第四列为两者之间的差值。类似的图一样的含义。

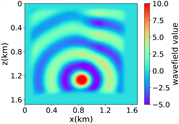
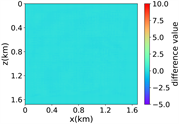
(a) (b) (c) (d)
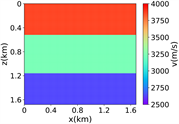


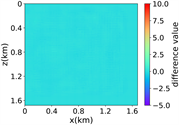
(e) (f) (g) (h)
(i)(j) (k) (l)
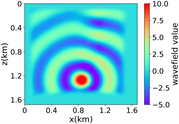
(iii) 简单分层模型下单频多源对应的波场图,震源位置为(0.42 km,0.84 km)、(0.84 km,0.42 km)、 (0.84 km,0.84 km)、(0.84 km,1.26 km)和(1.26 km,0.84 km),频率为8.25 Hz
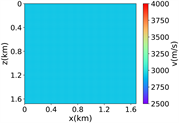
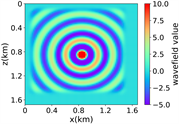
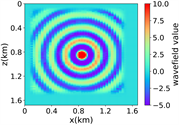
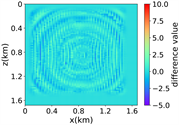
(a) (b) (c) (d)


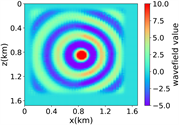
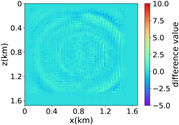
(e) (f) (g) (h)
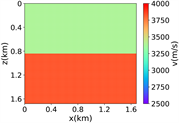
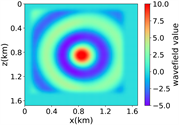

(i)(j) (k) (l)
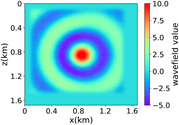
(iv) 简单分层模型下多频单源对应的波场图,震源位置为(0.84 km,0.84 km),且从上至下频率分别为 13.42 Hz,11.14 Hz和7.19 Hz
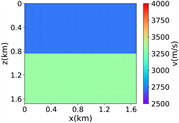
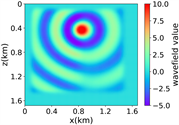
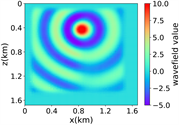

(a) (b) (c) (d)


(e) (f) (g) (h)



 (i)(j) (k) (l)(v) 简单分层速度模型下多频多源对应的波场图,震源位置为(0.42 km,0.84 km)、(0.84 km,0.42 km)、 (0.84 km,0.84 km)、(0.84 km,1.26 km)和(1.26 km,0.84 km),且从上至下频率分别为7.82 Hz,9.59 Hz和4.38 Hz
(i)(j) (k) (l)(v) 简单分层速度模型下多频多源对应的波场图,震源位置为(0.42 km,0.84 km)、(0.84 km,0.42 km)、 (0.84 km,0.84 km)、(0.84 km,1.26 km)和(1.26 km,0.84 km),且从上至下频率分别为7.82 Hz,9.59 Hz和4.38 Hz (vi) 训练集和验证集的损失函数变化曲线
(vi) 训练集和验证集的损失函数变化曲线
Figure 2. Computational results of layered model
图2. 分层模型的计算结果
4.2. Marmousi模型
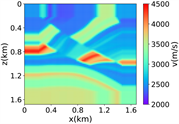
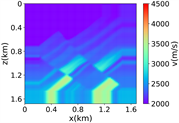
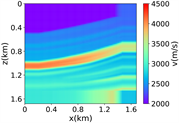
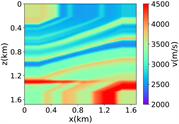
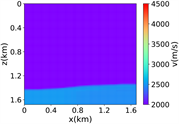
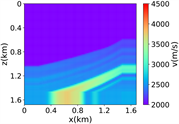
进一步评估RFNO在Marmousi模型中的波场模拟结果, 20米,维度大小为501 × 166,如图3中(i)所示,随机切片选取1000个84 × 84的速度模型作为样本数据,部分随机切片得到数据集如图3中(ii)所示,速度取值范围为1500 m/s至4600 m/s。在这个实验中,其他设置与简单分层模型一致。
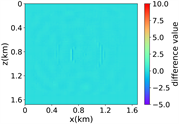
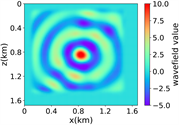
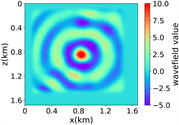
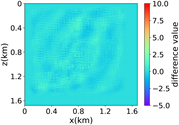
图3中的(iii)到(vii)展示了不同频率、震源位置在Marmousi模型中的实验结果,首先图(iii)为单源单频时RFNO进行的数值性能测试,在这个实验中,频率为8.25 Hz,震源位置为(0.84 km,0.84 km),以及结合图(vii)中训练集的损失函数变化呈不断下降的趋势,结果表明RFNO模型的参数不断优化,与实际波场值之间的误差逐渐减小,说明训练算法的收敛性。其次,在多源单频的情况下,图(iv)展示了在使用新的数据集进行测试时断层引起的散射现象,使得模拟结果与实际波场测试值之间存在一定的差异。针对单源多频模拟问题,从图(v)以及结合表2展示的不同源和频率下的损失函数值来看,频率因素对于模拟结果具有重要影响,特别是在高频情况下,频率的变化会导致波场传播更加复杂,RFNO的模拟结果与实际波场值存在较大差异。最后,在多源多频的图(vi)情况下,低频时可以成功模拟大部分波场,并且模拟结果与实际波场值相符合,然而在高频和与断层相关的情况时,模拟结果对于捕捉细节和快速变化的波场特征变得更加困难和有挑战性,模拟结果还是能够捕捉到波场的主要特征。

(i) 维度为501 × 166的Marmousi模型
(a) (b) (c)
(d) (e) (f)
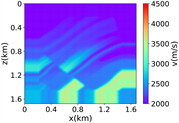
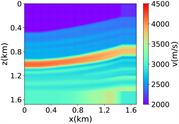
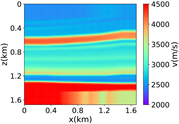
(g)(h) (i)
(ii) 部分随机切片的数据集
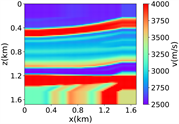
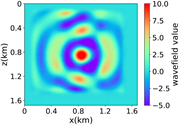

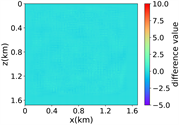
(a) (b) (c) (d)
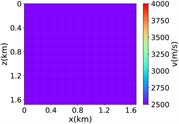

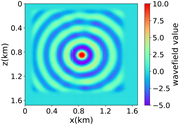
(e) (f) (g) (h)

(i)(j) (k) (l)
(iii) Marmousi速度模型下单频单源对应的波场图,震源位置为(0.84 km,0.84 km), 频率为8.25 Hz


(a) (b) (c) (d)
(e) (f) (g) (h)
(i)(j) (k) (l)
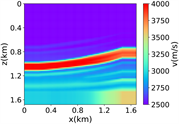
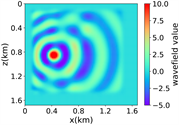
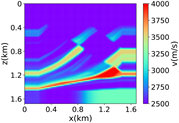
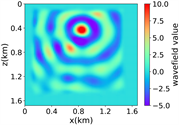
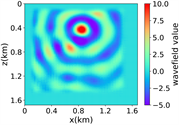
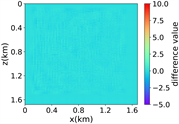
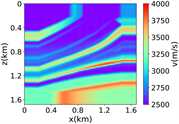
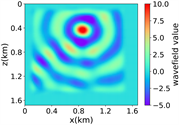
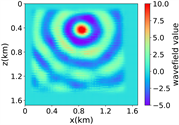
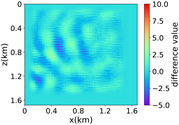
(iv) Marmousi速度模型下单频多源对应的波场图,震源位置为(0.42 km,0.84 km)、(0.84 km,0.42 km)、 (0.84 km,0.84 km)、(0.84 km,1.26 km)和(1.26 km,0.84 km),频率为8.25 Hz
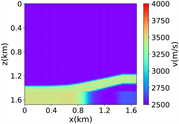
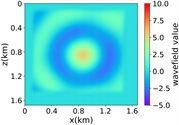

(a) (b) (c) (d)
(e) (f) (g) (h)

(i)(j) (k) (l)
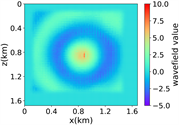
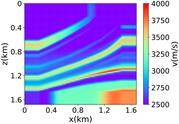
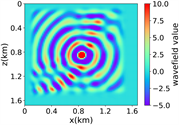
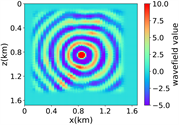
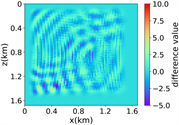
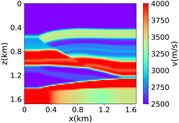
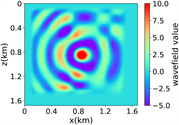
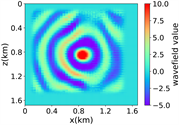
(v) Marmousi速度模型下多频单源对应的波场图,震源位置为(0.84 km,0.84 km),且从上至下频率分别为 3.44 Hz,14.55 Hz和9.84 Hz
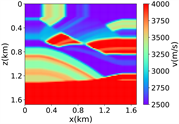
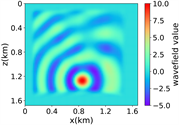
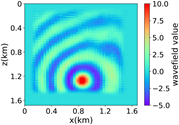
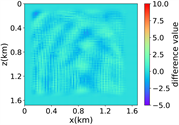
(a) (b) (c) (d)
(e) (f) (g) (h)



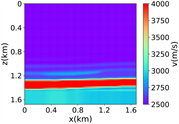
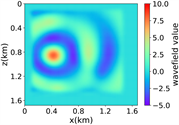
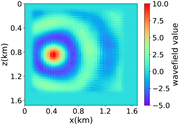
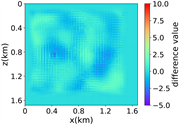
 (i) (j) (k) (l)(vi) Marmousi速度模型下多频多源对应的波场图,震源位置为(0.42 km,0.84 km)、(0.84 km,0.42 km)、 (0.84 km,0.84 km)、(0.84 km,1.26 km)和(1.26 km,0.84 km),且从上至下频率为6.64 Hz,5.78 Hz和6.39 Hz
(i) (j) (k) (l)(vi) Marmousi速度模型下多频多源对应的波场图,震源位置为(0.42 km,0.84 km)、(0.84 km,0.42 km)、 (0.84 km,0.84 km)、(0.84 km,1.26 km)和(1.26 km,0.84 km),且从上至下频率为6.64 Hz,5.78 Hz和6.39 Hz (vii) 训练集和验证集的损失函数变化曲线
(vii) 训练集和验证集的损失函数变化曲线
Figure 3. Computational results of Marmousi model
图3. Marmousi模型的计算结果
Table 2. Loss function values for different sources and frequencies
表2. 不同源和频率下的损失函数值
此外,相比于有限差分方法(FDM),RFNO展现出更快的波场推断速度。在Marmousi模型数据集中,选取100个模型进行波场模拟对比实验,传统的有限差分方法需要40.96秒,而RFNO仅需要2.33秒,是传统差分法的17倍,说明RFNO在波场推断方面具有显著的优势,能够更高效地进行模拟和预测。
5. 总结
频率域波动方程的传统数值求解方法具有模型参数和网格依赖性。本文结合残差网络和傅里叶神经算子提出了一种改进的傅立叶神经算子方法(RFNO)。针对二维频率域声波方程数值求解问题,基于简单分层模型和Marnousi模型进行数值实验,实验结果表明,本文提出的RFNO方法在处理多频率和多源问题时能够获得令人满意的波场模拟和较低的损失函数值结果,特别是在低频问题上表现出色。然而,在Marmousi模型实验中,由于波场较复杂,本实验使用的三个傅里叶层组成的网络不能较好地学习该复杂的波场特征,导致精度较低,可以增加网络的层数来提高网络的表示能力,以提高RFNO模型对复杂波场的建模能力。此外,与传统的数值求解方法相比,经过训练的RFNO模型在波场推理方面对不同物理参数的波场具有高效的推理速度。RFNO方法的高效性使得其可以作为反问题求解过程中的一种正问题求解的方法选择。
文章引用
潘代英,何清龙. 基于改进的傅里叶神经算子数值求解频率域声波方程
Numerical Solution of Frequency-Domain Acoustic Wave Equation Based on Improved Fourier Neural Operator[J]. 运筹与模糊学, 2023, 13(06): 5978-5990. https://doi.org/10.12677/ORF.2023.136594
参考文献
- 1. Elmas, D. and Uzun, B. (2022) Inverse Solution of Thermoacoustic Wave Equation for Cylindrical Layered Media. Frontiers in Physics, 10, Article 736555. https://doi.org/10.3389/fphy.2022.736555
- 2. Shaiban, A., Derid-der, S.A.L. and Curtis, A. (2022) Wavefield Reconstruction and Wave Equation Inversion for Seismic Surface Waves. Geophysical Journal International, 229, 1870-1880. https://doi.org/10.1093/gji/ggac031
- 3. Lee, H. and Liu, Y. (2022) Energy-Preserving Mixed Finite Element Methods for the Elastic Wave Equation. Applied Mathematics and Computation, 422, Article ID: 126963. https://doi.org/10.1016/j.amc.2022.126963
- 4. Gao, G., Han, B. and Tong, S. (2023) A Ghost-Point Based Second Order Accurate Finite Difference Method on Uniform Orthogonal Grids for Electromagnetic Scattering around Curved Perfect Electric Conductors with Corners. Journal of Computational Physics, 490, Article ID: 112314. https://doi.org/10.1016/j.jcp.2023.112314
- 5. Tao, B., Yu, X., Wang, W., Wang, H., Chen, X., Wang, F. and Wu, Y. (2023) A Deep Learning-Based Automatic Segmentation of Zygomatic Bones from Cone-Beam Computed Tomography Images: A Proof of Concept. Journal of Dentistry, 135, Article ID: 104582. https://doi.org/10.1016/j.jdent.2023.104582
- 6. Rossbach, J., Kollmeier, B. and Meyer, B.T. (2022) A Model of Speech Recognition for Hearing-Impaired Listeners Based on Deep Learning. The Journal of the Acoustical Society of America, 151, 1417-1427. https://doi.org/10.1121/10.0009411
- 7. Russo, A.G., Ciarlo, A., Ponticorvo, S., Salle, F.D., Tedeschi, G. and Esposito, F. (2022) Explaining Neural Activity in Human Listeners with Deep Learning via Natural Language Pro-cessing of Narrative Text. Scientific Reports, 12, Article No. 17838. https://doi.org/10.1038/s41598-022-21782-4
- 8. Li, J. and Chen, Y. (2020) Solving Second-Order Nonlinear Evolution Partial Differential Equations Using Deep Learning. Communications in Theoretical Physics, 72, Article ID: 105005. https://doi.org/10.1088/1572-9494/aba243
- 9. Moon, S. (2021) Relu Network with Bounded Width Is a Universal Approximator in View of an Approximate Identity. Applied Sciences, 11, Article 427. https://doi.org/10.3390/app11010427
- 10. Grohs, P., Hornung, F., Jentzen, A. and Zimmermann, P. (2023) Space-Time Error Estimates for Deep Neural Network Approximations for Differential Equations. Advances in Computational Mathematics, 49, Article No. 4. https://doi.org/10.1007/s10444-022-09970-2
- 11. Jiang, X., Jiang, J., Yu, J., Wang, J. and Wang, B. (2023) MSK-UNET: A Modified U-Net Architecture Based on Selective Kernel with Multi-Scale Input for Pavement Crack Detection. Journal of Circuits, Systems and Computers, 32, Article ID: 2350006. https://doi.org/10.1142/S0218126623500068
- 12. Song, C., Alkhalifah, T. and Waheed, U.B. (2022) A Ver-satile Framework to Solve the Helmholtz Equation Using Physics-Informed Neural Networks. Geophysical Journal International, 228, 1750-1762. https://doi.org/10.1093/gji/ggab434
- 13. Yang, Y., Gao, A.F., Castellanos, J.C., Ross, Z.E., Azizzadenesheli, K. and Clayton, R.W. (2021) Seismic Wave Propagation and Inversion with Neural Operators. arXiv: 2108.05421.
- 14. Aleardi, M., Vinciguerra, A., Stucchi, E. and Hojat, A. (2022) Probabilistic Inversions of Elec-trical Resistivity Tomography Data with a Machine Learning-Based forward Operator. Geophysical Prospecting, 70, 938-957. https://doi.org/10.1111/1365-2478.13189
- 15. Mosser, L., Kimman, W., Dramsch, J., Purves, S., Fuente, A.D. and Ganssle, G. (2018) Rapid Seismic Domain Transfer: Seismic Velocity Inversion and Modeling Using Deep Generative Neural Networks. 80th EAGE Conference and Exhibition 2018, 2018, 1-5. https://doi.org/10.3997/2214-4609.201800734
- 16. Li, M.D., Chang, K., Bearce, B., Chang, C.Y., Huang, A.J. and Campbell, J.P. (2020) Siamese Neural Networks for Continuous Disease Severity Evaluation and Change De-tection in Medical Imaging. NPJ Digital Medicine, 3, Article No. 48. https://doi.org/10.1038/s41746-020-0255-1
- 17. Li, Z., Kovachki, N., Azizzadenesheli, K., Liu, B., Bhattacharya, K. and Stuart, A. (2020) Multipole Graph Neural Operator for Parametric Partial Differential Equations. arXiv: 2006.09535.
- 18. Li, Z., Kovachki, N., Azizzadenesheli, K., Liu, B. and Anandkumar, A. (2020) Neural Operator: Graph Kernel Network for Partial Differential Equations. arXiv: 2003.03485.
- 19. Song, C. and Wang, Y. (2022) High-Frequency Wavefield Extrapolation Using the Fourier Neural Operator. Journal of Geophysics and Engineering, 19, 269-282. https://doi.org/10.1093/jge/gxac016
- 20. Siahkoohi, A., Louboutin, M. and Herrmann, F.J. (2022) Velocity Continuation with Fourier Neural Operators for Accelerated Uncertainty Quantifi-cation. arXiv: 2203.14386. https://doi.org/10.1190/image2022-3750475.1
- 21. O’Brien, G.S., Bean, C.J., Meiland, H. and Witte, P. (2023) Imaging and Seismic Modelling Inside Volcanoes Using Machine Learning. Sci-entific Reports, 13, Article No. 630. https://doi.org/10.1038/s41598-023-27738-6
- 22. Wen, G., Li, Z., Az-izzadenesheli, K., Anandkumar, A. and Benson, S.M. (2022) U-FNO—An Enhanced Fourier Neural Operator-Based Deep-Learning Model for Multiphase Flow. Advances in Water Resources, 163, Article ID: 104180. https://doi.org/10.1016/j.advwatres.2022.104180
- 23. Li, Z., Kovachki, N., Azizzadenesheli, K., Liu, B., Bhattacharya, K., Stuart, A. and Anandkumar, A. (2020) Fourier Neural Operator for Parametric Partial Differential Equations. arXiv: 2010.08895.
- 24. Li, M. and Jiang, L. (2021) Deep Learning Nonlinear Multiscale Dynamic Problems Using Koopman Operator. Journal of Computational Physics, 446, Article ID: 110660. https://doi.org/10.1016/j.jcp.2021.110660
