Hans Journal of Wireless Communications
Vol.08 No.01(2018), Article ID:23860,19
pages
10.12677/HJWC.2018.81003
Design and Performance Analysis of Omnidirectional Space-Time Block Code in Massive MIMO Systems
Tianyang Cao
School of Information Science and Engineering, Southeast University, Nanjing Jiangsu

Received: Feb. 11th, 2018; accepted: Feb. 20th, 2018; published: Feb. 27th, 2018

ABSTRACT
Common signals should be transmitted omnidirectionally to guarantee cell-wide coverage in massive MIMO systems under celluar communication units. Space-Time Block Code (STBC) has received widespread application in MIMO systems, in this paper, we focus on the omnidirectional STBC in massive MIMO downlink, which provides a new thinking for reducing the burden of downlink pilot overhead. We firstly design an omnidirectional precoding (OP) matrix for 2*2 Alamouti Code, which guarantees equal receiving power for user terminals in all spatial directions at any instant time as well as equal instantaneous power for each transmitting antenna. To obtain diversity order of four, OP matrices utilizing $4*4$ STBC and OSTBC Code are also proposed, respectively. What’s more, the condition of OP matrices is rewritten considering constant angle domain, and several examples of OP matrices are proposed. We analyse the system performance utilizing omnidirectional STBC in four aspects: bit error rate, peak-to-average ratio (PAPR), channel capacity and outage probability. Simulation results show that one proposed design can 1) reduce bit error bit; 2) maximize channel capacity; 3) preserve the PAPR of transmitted signals.
Keywords:Massive MIMO, Omnidirectional Precoding, Space-Time Block Code, Diversity Order, Zadoff-Chu Sequence, Phase Complementary Sequence
大规模MIMO系统下的全向STBC编码设计 与性能分析
曹天旸
东南大学信息科学与工程学院,江苏 南京
收稿日期:2018年2月11日;录用日期:2018年2月20日;发布日期:2018年2月27日

摘 要
在蜂窝通信单元下的大规模多输入多输出(MIMO)系统中,公用信号应该被全向传输以确保全范围覆盖。空时分组编码(STBC)目前已被广泛地应用于MIMO系统中,本文研究下行同步传输情景下的全向STBC编码,该方案也为有效降低下行链路导频开销提供了新的思路。首先我们在采样后的离散角度域为2*2的Alamouti编码设计了一种全向编码,该方案可以在空间角度域获得恒定的传输功率,同时保证各天线上的瞬时功率相等。随后,为获得4分集阶数,我们针对天线数为4的星座旋转STBC编码,提出了一种全向编码设计,并给出了对应的STBC编码中信息符号的生成方法。同时,我们将该方法推广到了使用复信号OSTBC编码时的情形。然后我们针对连续角度域重新推导了全向传输的等价条件,运用相位互补序列分别构造了Alamouti码和星座旋转STBC码的全向编码。为评估上述编码的性能,我们从误码率,遍历信道容量,峰均比,中断概率四个方面推导了相关表达式。最后我们从上述四个方面对所提出的构造进行了性能仿真,结果证明其中一种编码能有效降低误码率,渐进地达到信道容量上界,并在OFDM系统中保持原信号峰均比。
关键词 :大规模MIMO系统,全向预编码,STBC编码,分集阶数,Zadoff-Chu序列,相位互补序列

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
大规模多输入多输出(MIMO)技术是下一代移动通信的核心技术之一,它通过在发射端和接收端同时使用多个天线,能够充分地利用空间资源,提高频谱利用率,从而改善无线通信质量。MIMO系统的应用,可以在环境信噪比难以改善的情况下提高信道容量 [1] ,因而受到了广泛关注。针对大规模MIMO系统的研究目前已较深入地展开,主要工作包括:文献 [2] [3] 研究了大规模MIMO系统中正交频分复用的应用,并提出了正交扩频序列的设计方法,文献 [4] [5] 研究了MIMO系统下的信道检测与信道估计问题,文献 [6] 利用相位编码优化给出了一种干扰抑制技术,能够稳定地抑制频率选择信道下的信道间干扰,文献 [7] 提出了一些时分双工(TDD) MIMO系统下降低导频开销的有效方法,此外,在当今频带资源紧张的情况下,毫米波频段通信 [8] 也成为了研究热点。
在MIMO系统关键技术的研究中,下行链路的STBC编码传输是一个重要的课题。STBC编码是一种在空间域和时间域同时进行信道编码的方法,由于STBC编码通常采取正交编码方式,因此在接收端使用最大似然算法进行解码十分方便。Alamouti等人首先提出了一种双天线传输方法 [9] ,该方法是双天线模式下唯一可以达到满发送速率的编码方式。由于STBC编码方式下的译码复杂度随天线数成指数关系增长,同时增加传输天线数目又会导致时频资源的浪费 [10] ,因此STBC编码通常以低维形式出现。为解决上述问题,文献 [11] [12] 提出了将传输信号限制在低维子空间中以降低导频开销的方法。在MIMO系统的信号传输中,为提高资源利用率通常在接收端会安排多个用户(UT),因此关于全向传输编码的研究具有十分重要的意义。全向传输条件要求基站(BS)发送的信号在不同的时隙内,在空间各角度上均获得相同的信噪比,以确保不同用户获得同样的接收功率。同时为充分利用发射天线的功放(PA)容量,基站各天线上的传输功率也应保持一致。因此,我们需要设计与信道无关的全向预编码(OP)矩阵来实现上述要求。目前关于MIMO系统中全向预编码方法已有几篇研究工作 [12] [13] ,但上述文献仅从离散采样角度考虑了对单流信号的全向编码,没有考虑连续角度域的设计,且几乎没有分析编码后系统的误码率、信道容量等性能。为此,本文将主要研究采用STBC编码的下行链路传输的全向预编码方法及其编码性能,该模型大幅度降低了等效信道矩阵列数,从而降低信道估计压力。
根据以上分析,本文剩余部分的安排如下:在第2部分,我们给出了MIMO系统模型,并结合相关文献的研究给出了离散角度域STBC编码条件下OP矩阵满足的条件。在3部分,我们首先针对2*2的Alamouti编码,提出了一种符合要求的构造实例,并讨论了其中的参数的取值要求,其次我们针对常用的4*4星座旋转STBC编码和复信号OSTBC编码,利用Hadamard矩阵和ZC序列分别提出了构造,并且指出在该构造方法下STBC编码中的传输符号的设计方法。在第4部分中,我们考虑连续角度域的情况推导了OP矩阵所满足的条件,根据该条件提出了一种Alamouti编码对应的全向编码构造,随后又将其推广得到STBC编码矩阵为4*4型时所需的OP矩阵。在第5部分中,我们对编码后系统误码率,峰均比(PAPR),信道容量,中断概率进行了分析,并说明发射天线数充分大时信道容量达到上界。第6部分中,我们针对所提出的几种OP矩阵的上述四种性能指标进行看仿真。结论在第6部分中给出。
符号约定:我们用 和*分别表示矩阵的Kronecker积和Hadamard积,用 和 分别表示M维单位矩阵和单位列向量,用 分别表示矩阵 的共轭、转置和共轭转置,用 表示以向量 为对角线向量的矩阵,用 、 、 和 分别表示矩阵的行列式值、迹、秩和拉直算子,用 表示向量 的二范数,用 表示数学期望,用记号DFT表示序列的离散傅里叶变换。
2. STBC编码下的MIMO系统模型
考虑一个具有M个发射天线,K个接收天线的通信系统,如图1所示。预编码矩阵为 ,低维STBC矩阵为 ,其中T表示传输符号从T个时隙 发送出去。设第k个接收天

Figure 1. System model of STBC coded massive MIMO systems
图1. 使用全向STBC编码的MIMO系统模型
线所对应的信道向量为 , 符合瑞利衰落分布。信道矩阵可表示为 。设各信道之间是相互独立的,则有第k个接收天线在T个时刻接收到的信号 为
(1)
其中 为经过OP矩阵映射后的发送符号, ,因此导频序列长度只需要不小于N即可,导频开销将显著降低。 为均值为0,方差为 的复加性高斯白噪声。不妨设接收端的K根天线关于基站段有相同的大尺度衰落,用 表示对角线上第k个元素为M,其余所有元素均为0的对角阵,则第k根天线在第t个时隙的接收功率为
(2)
其中 表示M点离散傅里叶变换矩阵, ,对列向量 作DFT变换等效于左乘 。 表示矩阵 的某一列。
我们采用文献 [12] 提出的设计准则,即预编码矩阵 和低维STBC编码矩阵 需要满足以下条件:
·全向传输条件:首先,所设计的OP矩阵需要满足在$M$个离散角度域上具有相同的传输功率,即列向量 的M个分量具有相同的幅值: ,此时容易验证K个接收天线上所接收的信号功率 为定值,符合设计要求。
·PA利用率条件:为达到较高的天线功放利用率,我们考虑保证M个发送天线上的传输信号相等,即对任一时刻t,均有 ,由各发送天线上的瞬时功率与OP矩阵 和STBC矩阵 都有关,因此本文将STBC矩阵中的传输符号与预编码矩阵联合设计。
3. 离散角度下的全向STBC编码设计
3.1. N = 2时的全向STBC编码设计
当 时,我们使用Alamouti码作为低维码,则有 。Alamouti码是一种发射天线数为2,可以提供满分集速率的正交空时码,编码器输出的两个符号在两个时间周期内被发送出去,如下式所示:
(3)
我们提出使用以下构造来设计 :
(4)
其中 为长度为M的ZC恒模序列,其定义为:
(5)
上式中能够 , 是与M互素的正整数。 为k阶循环位移阵,其定义为:
(6)
矩阵 , 需要满足以下三个条件:
① , 。
② 。
③ 矩阵 是规范列正交的。
证明:取发射天线个数M为偶数,即 ,为方便推导不妨令 (若 ,下述推导是完全类似的)。
首先我们有:
(7)
其中:
(8)
(9)
(10)
容易验证上式中对任意给定的 ,当n取遍 , 恰好为 的一个排列,故 可记作 ,其中 是与k无关的复函数。注意到 ,则有:
(11)
(12)
与式(8) (9) (10)中的推导类似,易得 ,其中 。于是由(12)式可得:
上式中 , 表示a模b的余数, 均为 的线性函数。由 的表达式容易验证 当且仅当 ,我们进一步令天线个数为4的倍数,则有:
(16)
上式显然与k无关,由此我们证明了 的M个分量恒模,对 ,证明是完全等价的,于是全向传输条件得到了满足。下面我们证明式(4)中给出的构造满足PA利用率条件:由(11)式给出的 的形式,容易验证:
(17)
(18)
由上两式及所提出的 的设计条件,容易得到当传输符号 满足: 。且 时, 为定值,因此低维传输符号矩阵 需要与OP矩阵 联合设计。文献给出了在Alamouti编码结构下对符号信息 进行单独设计的方法,该方法虽构造简便,但其不能有效降低传输信号的峰均比。本文给出一种满足设计准则的新的构造方法,将 联合设计,虽然该方法在接收端最大似然译码时略显复杂,但在之后的性能分析与仿真结果中,可以看到该方案降低了系统峰均比,如下所示:
(19)
其中T为码元周期。另外我们注意到所提出的编码矩阵 的两列向量是复正交的,这样的构造使得在接收端只需进行简单的相关处理即可将不同时隙发送的符号进行分离。
3.2. N = 4时采用星座旋转编码的全向STBC编码设计
当N = 4时,令 ,我们采用4天线的Jafarkhani码,即每次取4个信息符号 进行编码,其中 取自星座图 ,而 取自星座图 ,即:
(20)
与Alamouti编码类似,上述Jafarkhani码编码也可以达到满发射速率。我们同样采用ZC序列提出一种构造: ,其中:
(21)
上式中 为二阶Hardmard矩阵。
证明:我们首先给出一个简单的引理:
引理1:对任意 ,都存在一个函数集 ,使对任意 , 而 当且仅当 。
引理1的证明:事实上,我们令 为1的D阶单位根,则取
(22)
容易验证上述一系列函数满足要求。
为简便起见我们令 , 的第j行行向量为 ,类似于(13)式的推导我们有:
(23)
注意到:
(24)
于是(23)式又可写作:
容易验证 为定值当且仅当 ,因此我们取 ,则由上式容易证明 为一恒模向量。
另一方面,由Hardmard矩阵的定义容易验证:
(25)
(26)
式(25)中 ,式(26)中 。由上式可知,采用(21)式提出的预编码矩阵,可以使符号组 和 独立设计,即按照(19)中所提出的方法构造,可以满足 且 。
3.3. N = 4时OSTBC编码的全向编码设计
在文献 [10] 中,作者给出了发射信号为复信号情况下的OSTBC编码设计,其可以达到3/4的发射速率,事实上这类矩阵总可以表示为:
(27)
其中 。于是我们可将式(21)中提出的构造进一步推广为
(28)
证明:
将 写作分块对角阵的形式,即:
(29)
并记 。这样,我们有:
(30)
其中 , 或 。这样, 事实上具有与(23)式中的 完全相同的性质,接下来的证明与3.2节中类似。
4. 连续角度下的全向STBC编码设计
当考虑连续角度域的设计时,本文第二部分所述的全向传输条件中的离散角度变量变为连续角度变量,即对 作DTFT变换,并考虑T个时隙 的发送总功率,我们得到修正后的全向传输条件:
(31)
4.1. N = 2时的全向STBC编码设计
当 时,我们仍然利用(3)式中给出的Alamouti编码。为得到(31)式的等效条件,我们将 写出列向量的形式: 。并记对列向量 的DTFT变换分别为 ,即:
(32)
利用(32)式,(31)式又可写作:
(33)
根据(33)式得到的等效表达式,我们得到考虑连续角度时的设计准则:
·全向传输条件:由于 ,为满足各方向用户所接收的总功率相等,只需满足 。
·PA利用率条件:PA利用率的约束条件与离散角度域相同,需要满足 为一恒模向量。
·最大化分集增益:为保证编码后仍能取得最大分集增益,我们希望使 根据上述设计准则,取天线数 ,我们提出一种构造方法:
(34)
其中 和 为一对长度为 的glory互补序列。当 ,glory序列可由递归方法生成:取初始序列 ,根据 , 进行递归生成,则 即为所求的glory互补序列。
证明:首先将 变形为:
(35)
(36)
其中 , 分别为 和 的DTFT变换函数。利用(35) (36)式可得:
(37)
表示取虚部。用 分别表示 和 的自相关函数,根据glory互补序列的性质有 ,我们进一步得到:
(38)
令 ,于是有 ,为与 无关的定值。这就证明了式(34)所提构造符合全向传输条件。另一方面,容易验证 及 ,综上,式(34)中的OP矩阵完全符合设计准则。
4.2. N = 4时的全向STBC编码设计
当 时,我们仍考虑采用式(20)中的星座旋转编码,此时与 时的推导类似,我们可以得到: 。设计准则与 的情况类似,我们给出一种构造方法:
(39)
其中 , , , 。
与(38)式类似,本文可以得到:
(40)
由上式可知,满足全向传输条件的关键是得到一组非循环完全互补序列,满足 ,其中 为长度为 的Kronecker序列。我们利用生成树的方法提出一种完全互补序列组的构造方法:令 ,首先我们得到一组4个长度为8的完全序列集:
(41)
在(41)的基础上进行递推,可以得到一组4个长度为16的互补序列集:
(42)
事实上,据此可以归纳出由 递推得到 的一般方法:首先我们将 分块记为:
(43)
其中 。注意到所提构造以 为基本单位,我们用记号 表示将序列 中的负号左移一次,用记号 表示对序列 取反,例如设 ,则 ,而 。运用上述记号,由 生成 的递推关系可表示为:
(44)
通过上述关系式,我们构造了一组4个长度为任意 的互补序列,该序列组中的任意两序列均为一对glory互补序列。用这四个序列分别作为式(39)中的序列 ,即可得到满足全向传输条件的OP矩阵。与 的情形类似,容易验证 恒模及 ,因此(39)式中的构造方法符合三个设计准则的要求。另外,注意到(39)中矩阵每行只有一个非零元素,根据下文的讨论可以看到,其能够保持传输信号的峰均比。
5. 采用全向STBC预编码的系统性能分析
5.1. 峰均比(PAPR)的分析
在OFDM通信系统中,降低子载波调制后信号的峰均比是一个重要的问题,因此我们至少应保证经过预编码矩阵映射后信号峰均比不会增加。考虑 个信息符号,码元周期为 ,经过 个相互正交的子载波调制后其峰均比可表示为:
(45)
经过预编码后的峰均比可表示为:
(46)
其中 为低维符号矩阵 的某一列向量的第k个分量。下面我们推导经过预编码后PAPR降低的充分条件。一方面由子载波的正交性容易验证:
(47)
(48)
另一方面我们有:
(49)
其中第一个不等号利用了复数域的柯西不等式,第二个不等号利用了复数的三角不等式。注意到 ,同时设 有 个非零元素,结合(29) (30) (33)可得 的一个充分条件为:
(50)
由此易知,为达到不增加PAPR的目的,只需使式(21)所提OP矩阵乘一归一化常数1/4即可,这对全向性能没有任何影响。特别地,若,则由(47) (48)可直接验证 ,显然式(39)中提出的构造能保持峰均比。
5.2. 误码率(BER)的分析
考虑欲发送的符号矩阵为 ,被误判决为 的概率,其中 , 为码本集合。利用文献 [10] 给出的定义,可以得到:
(51)
其中 , , 为高斯补误差函数, 为 的 个特征值, 为其联合概率密度函数。 为 的最小特征值,第一个不等号由 得到,第二个不等号由引理2得出。
引理2:设 为半正定Hermite矩阵, 为Hermite矩阵,则有:
(52)
由(51)式可知,得到误码率上界的关键为求得 的概率密度。我们有:
(53)
其中:
(54)
等式(a)由文献 [14] 给出的引理得到(为简化推导假定 ),且有:
(55)
其中 为第二类不完全欧拉积分。注意到 为 的Hankel矩阵,即该矩阵中任意元素总能表示为 的形式。利用Hankel的性质:其行列式展开中每一项 均满足 ,经计算可得 可展开为:
(56)
其中系数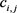 可由下式确定:
可由下式确定:
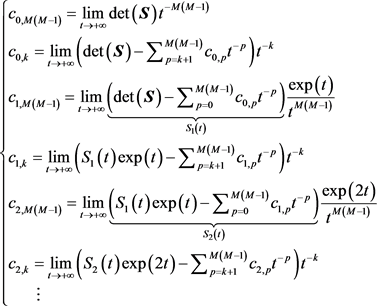 (57)
(57)
将(56)式代入(51)式,经推导可得:
 (58)
(58)
其中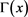 为gamma函数。(58)式给出了采用全向STBC编码的系统误码率上界。容易看到,若STBC编码经过
为gamma函数。(58)式给出了采用全向STBC编码的系统误码率上界。容易看到,若STBC编码经过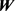 矩阵映射后满足
矩阵映射后满足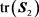 充分大,则系统误码率性能将得到显著改善。
充分大,则系统误码率性能将得到显著改善。
5.3. 遍历化信道容量
利用文献 [15] 的结果,我们给出独立同分布瑞利信道下的信道容量表达式:
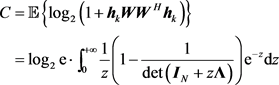 (59)
(59)
其中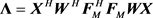 ,注意
,注意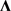 为正定阵,在(45)的基础上运用阿达玛不等式,可进一步得到遍历化信道容量的上界:
为正定阵,在(45)的基础上运用阿达玛不等式,可进一步得到遍历化信道容量的上界:
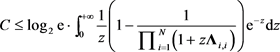 (60)
(60)
上述不等号取等的充要条件是 为对角阵。利用
为对角阵。利用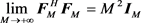 和低维符号矩阵的正交性:
和低维符号矩阵的正交性: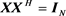 ,
,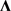 为对角阵等效于
为对角阵等效于 为对角阵。对式(21)提出的构造,经计算可得:
为对角阵。对式(21)提出的构造,经计算可得:
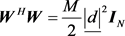 (61)
(61)
其中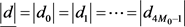 ,
,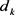 的定义与(23)式中相同。这就证明了(21)式提出的构造在天线数M趋向于无穷时能渐进地达到上界,根据引理4,对式(28)中提出的OP矩阵也有同样的结论。将(61)式代入(60)式,我们有:
的定义与(23)式中相同。这就证明了(21)式提出的构造在天线数M趋向于无穷时能渐进地达到上界,根据引理4,对式(28)中提出的OP矩阵也有同样的结论。将(61)式代入(60)式,我们有:
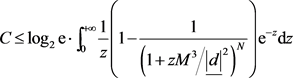 (62)
(62)
根据(48)式,容易看出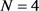 时的STBC全向编码信道容量优于
时的STBC全向编码信道容量优于 时的情形。另一方面,由于
时的情形。另一方面,由于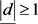 且有
且有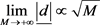 (引理3),显然采用全向编码后将获得信道容量增益,且当天线数较大时尤其明显。
(引理3),显然采用全向编码后将获得信道容量增益,且当天线数较大时尤其明显。
引理3:利用文献 [16] 的结果,对二次高斯和函数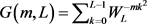 ,有:
,有:
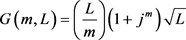 (63)
(63)
其中 ,
,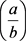 表示勒让德符号,当
表示勒让德符号,当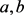 互素,
互素,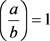 。
。
引理4:式(28)中的构造能够满足遍历互信息量渐进地达到上界。
证明:只需考虑形如 形式的构造,因为
形式的构造,因为
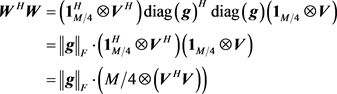 (64)(65)
(64)(65)
其中第二个等号是由于在(28)式中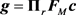 为恒模序列,第三个等号由
为恒模序列,第三个等号由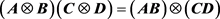 得到。这样,为满足
得到。这样,为满足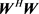 为对角阵,我们只需满足
为对角阵,我们只需满足 为对角阵,而(28)式中的
为对角阵,而(28)式中的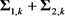 为正交阵,即证。
为正交阵,即证。
5.4. 中断概率
在下行同步传输中,中断概率常被用来考察在一定用户速率要求下信噪比低于门限值的概率。在本文中,我们记门限值为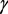 ,则第k(
,则第k( )个用户发生中断的中断概率的表达式为:
)个用户发生中断的中断概率的表达式为:
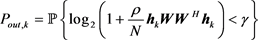 (66)
(66)
其中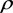 为基站端的发送功率。对(21)式提出的构造,
为基站端的发送功率。对(21)式提出的构造, 为一稀疏矩阵,满足:
为一稀疏矩阵,满足:
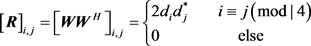 (67)
(67)
而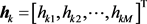 满足:
满足: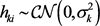 。利用文献 [17] 的结果,我们有:
。利用文献 [17] 的结果,我们有:
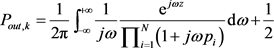 (68)
(68)
其中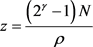 ,
,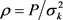 ,P为给定的功率约束常数,
,P为给定的功率约束常数, 。
。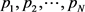 为
为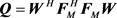 的N个特征值。为计算(68)式,我们给出一个引理:
的N个特征值。为计算(68)式,我们给出一个引理:
引理5:见式(71)。
证明:
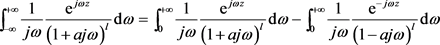 (69)
(69)
其中:
 (70)
(70)
将(70)的结果代入(69),则有:
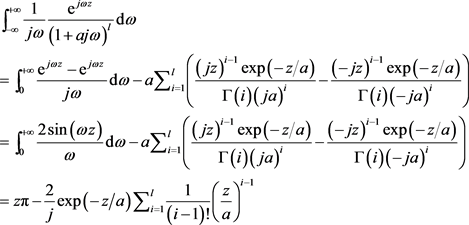 (71)
(71)
应用引理3的结果,首先对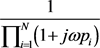 作部分分式分解,设
作部分分式分解,设 中有
中有 个不同的值
个不同的值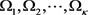 且其代数重数分别为:
且其代数重数分别为: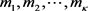 ,则:
,则:
 (72)
(72)
其中:
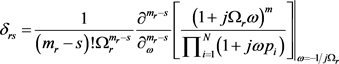 (73)
(73)
由(68) (71) (72)式,可得系统中断概率的闭式表达:
 (74)
(74)
6. 仿真结果
本部分我们将从误码率,遍历互信息量,中断概率,峰均比性能四个方面分析施加预编码矩阵后的系统性能。考虑OFDM系统下的理想扇区天线,每个扇区圆心角为120˚,阵元间隔为 ,其中
,其中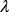 是电磁波波长。基站端的配置为具有
是电磁波波长。基站端的配置为具有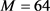 根天线的ULA阵列,由于用户端各用户的接收信号互相独立,我们设
根天线的ULA阵列,由于用户端各用户的接收信号互相独立,我们设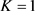 。信道特征为独立同分布信道,各分量均为均值为0,方差为1的循环对称复高斯变量。
。信道特征为独立同分布信道,各分量均为均值为0,方差为1的循环对称复高斯变量。
图2给出了不同信噪比条件下,无预编码、分别使用式(4),式(21),式(34),式(39)所提出的编码情况下的误码率性能。码元速率设为1 bps/HZ。式(4)和(21)中循环位移阵的 ,ZC序列中参数
,ZC序列中参数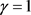 。式(4)中的矩阵
。式(4)中的矩阵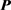 设为:
设为:
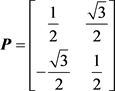 (75)
(75)
由图2可知,在应用所提出的四种全向预编码后,系统的误码率性能均有所改善,其中(21)式OP矩阵能最大限度地降低误码率。
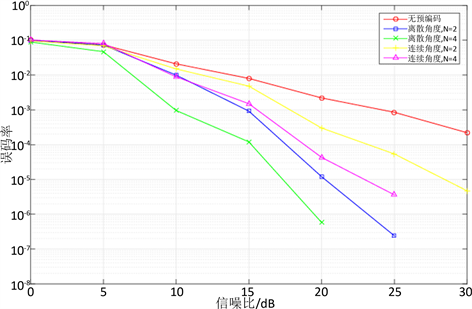
Figure 2. Bit Error Rate (BER) Simulation
图2. 系统误码率仿真
图3给出了四种OP矩阵在天线数目增加时的遍历信道容量变化曲线,信噪比条件设定为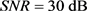 ,根据前述分析,为满足全向传输条件天线数至少应为4的倍数,故我们取
,根据前述分析,为满足全向传输条件天线数至少应为4的倍数,故我们取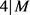 时的数据。由图可知,(21),(34),(39)中的OP矩阵均能在天线个数足够大时渐进地逼近信道容量上界,这与理论分析的结果是一致的。
时的数据。由图可知,(21),(34),(39)中的OP矩阵均能在天线个数足够大时渐进地逼近信道容量上界,这与理论分析的结果是一致的。
为比较所提出编码的峰均比性能,我们引入互补累积分布函数(CCDF),其定义为PAPR超过一定数值PAPR0的概率,即:
 (76)
(76)
分别考察使用4种不同OP矩阵情况下的峰均比,对每种构造,采用本身具有较低峰均比的DFTS-OFDM QPSK调制方式与式(19)中提出的编码方式相对比。由图4可知,使用式(19)提出的调制编码方式对连续角度的OP矩阵PAPR优化较明显,对式(34),(39)中的OP矩阵,其在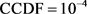 时对应的信噪比门限值较之DFTS-OFDM QPSK调制情况分别减少约0.7 dB和1.2 dB。
时对应的信噪比门限值较之DFTS-OFDM QPSK调制情况分别减少约0.7 dB和1.2 dB。
图5给出了信噪比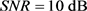 情况下,四种OP矩阵在天线数目变化时的中断概率曲线。式(66)中的门限值设为
情况下,四种OP矩阵在天线数目变化时的中断概率曲线。式(66)中的门限值设为 。由图容易看出
。由图容易看出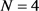 时的系统中断概率明显优于
时的系统中断概率明显优于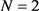 时的情形,且当天线数目增长时四种构造的中断概率均能较快地收敛于下界,而(21)式中提出的编码中断概率性能最优。
时的情形,且当天线数目增长时四种构造的中断概率均能较快地收敛于下界,而(21)式中提出的编码中断概率性能最优。
7. 结论
本文主要研究了大规模MIMO系统下使用联合预编码-STBC编码情况下的下行链路同步传输。我们从离散角度域和连续角度域分别讨论了全向STBC编码的构造,对 ,
,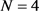 时的常用STBC编码,我们分别提出了全向编码的构造实例,并给出了联合设计低维传输符号的方法,其能够满足:接收端各用户获得相同的传输功率。基站端各天线PA利用率最大化。当
时的常用STBC编码,我们分别提出了全向编码的构造实例,并给出了联合设计低维传输符号的方法,其能够满足:接收端各用户获得相同的传输功率。基站端各天线PA利用率最大化。当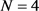 时,所提出的编码能够使4个低维传输符号被分组独立地设计。随后,我们进一步将
时,所提出的编码能够使4个低维传输符号被分组独立地设计。随后,我们进一步将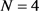 时的构造推广到了复信号的OSTBC编码。在性能分析部分中,我们分别推导了误码率与中断概率的闭式解,同时我们给出了天线数目增加时遍历化信道容量的上界以及为渐进地逼近上界,预编码矩阵所需满足的条件。我们还分析了经过预编码矩阵映射
时的构造推广到了复信号的OSTBC编码。在性能分析部分中,我们分别推导了误码率与中断概率的闭式解,同时我们给出了天线数目增加时遍历化信道容量的上界以及为渐进地逼近上界,预编码矩阵所需满足的条件。我们还分析了经过预编码矩阵映射

Figure 3. Ergodic channel capacity versus the number of antennas for different coding schemes
图3. 天线数量变化时遍历互信息量仿真

Figure 4. Peak-to-average rate (PAPR) for different coding/modulation schemes
图4. 不同编码与调制方式下的峰均比仿真
Figure 5. Comparison of outage probability for different number of antennas
图5. 天线数目变化时系统中断概率仿真
后系统峰均比的变化情况,给出了OFDM系统下保持原发送信号峰均比的预编码矩阵的一个充分条件。在连续角度域,我们从全向传输,最大化PA利用率和保持满分集增益三个方面重新推导了预编码矩阵满足的条件,在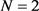 和
和 的情况下,利用相位互补序列分别给出了构造方法。在性能仿真部分,我们从误码率、峰均比、信道容量、中断概率四个方面分别进行了详尽的仿真,结果证明:所提出的四种预编码矩阵均能有效降低误码率。式(21),(61),(66)提出的编码均能渐进地逼近信道容量上界。式(19)中给出的联合设计低维传输符号的方法能有效降低系统的峰均比,且其针对连续角度的编码优化较明显。式(21)中提出的预编码矩阵具有最佳的性能,其在误码率,信道容量,中断概率的仿真中均为最优。最后,本文的研究仍可以进一步拓展,例如使用二维阵列天线(UPA)情形下的预编码矩阵构造,以及使用预编码矩阵后的接收译码方案等仍有待进一步研究。
的情况下,利用相位互补序列分别给出了构造方法。在性能仿真部分,我们从误码率、峰均比、信道容量、中断概率四个方面分别进行了详尽的仿真,结果证明:所提出的四种预编码矩阵均能有效降低误码率。式(21),(61),(66)提出的编码均能渐进地逼近信道容量上界。式(19)中给出的联合设计低维传输符号的方法能有效降低系统的峰均比,且其针对连续角度的编码优化较明显。式(21)中提出的预编码矩阵具有最佳的性能,其在误码率,信道容量,中断概率的仿真中均为最优。最后,本文的研究仍可以进一步拓展,例如使用二维阵列天线(UPA)情形下的预编码矩阵构造,以及使用预编码矩阵后的接收译码方案等仍有待进一步研究。
文章引用
曹天旸. 大规模MIMO系统下的全向STBC编码设计与性能分析
Design and Performance Analysis of Omnidirectional Space-Time Block Code in Massive MIMO Systems[J]. 无线通信, 2018, 08(01): 18-36. http://dx.doi.org/10.12677/HJWC.2018.81003
参考文献 (References)
- 1. 戚晨皓, 黄永明, 金石. 大规模MIMO系统研究进展[J]. 数据采集与处理, 2015, 30(3): 544-551.
- 2. Al-Askery, A.J., Tsimenidis, C.C., Boussakta, S. and Chambers, J.A. (2017) Performance Analysis of Coded Massive MIMO-OFDM Systems Using Effective Matrix Inversion. IEEE Transactions on Communications, 65, 5244-5256. https://doi.org/10.1109/TCOMM.2017.2749370
- 3. Suganya, M. and Gandhiraj, R. (2016) Applicability of MIMO and OFDM Technology to SATCOM. 2016 International Conference on Communication and Signal Processing (ICCSP), Melmaruvathur, 6-8 April 2016, 916-920.
- 4. Yang, L., Zeng, Y. and Zhang, R. (2017) Channel Estimation for Millimeter Wave MIMO Communications with Lens Antenna Arrays. IEEE Transactions on Vehicular Technology, PP(99): 1-1.
- 5. Li, T., Wang, X., Fan, P. and Riihonen, T. (2017) Position-Aided Large-Scale MIMO Channel Estimation for High-Speed Railway Communication Systems. IEEE Transactions on Vehicular Technology, 66, 8964-8978. https://doi.org/10.1109/TVT.2017.2703595
- 6. Yu, Z.H., Li, J., Zhang, Y.H. and Liao, G.S. (2017) Mainlobe Interference Suppression via Transmit Phase Codes Optimisation in MIMO Radar Systems. Electronics Letters, 53, 1427-1429. https://doi.org/10.1049/el.2017.2787
- 7. Komulainen, P., Tolli, A., M. Latva-aho and Juntti, M. (2009) Channel Sounding Pilot Overhead Reduction for TDD Multiuser MIMO Systems. 2009 IEEE Globecom Workshops, Honolulu, HI, 30 November-4 December 2009, 1-6. https://doi.org/10.1109/GLOCOMW.2009.5360756
- 8. Hu, A. and Pan, P. (2017) Concavity Approximation Based Power Allocation in Millimeter-Wave MIMO Systems. IEEE Access, 5, 25731-25740. https://doi.org/10.1109/ACCESS.2017.2773491
- 9. Alamouti, S.M. (1998) A Simple Transmit Diversity Technique for Wireless Communications. IEEE Journal on Selected Areas in Communications, 16, 1451-1458. https://doi.org/10.1109/49.730453
- 10. 李秋萍. MIMO系统中的空时编码技术研究[D]: [硕士学位论文]. 南京: 南京邮电大学, 2010.
- 11. Karlsson, M. and Larsson, E.G. (2014) On the Operation of Massive MIMO with and without Transmitter CSI. IEEE SPAWC, Toronto, ON, 1-5.
- 12. Meng, X., Gao, X.Q. and Xia, X.-G. (2016) Omnidirectional Precoding Based Transmission in Massive MIMO Systems. IEEE Transactions on Communications, 64, 174-186. https://doi.org/10.1109/TCOMM.2015.2498159
- 13. Meng, X., Xia, X.G. and Gao, X. (2014) Constant-Envelope Omni-Directional Transmission with Diversity in Massive MIMO Systems. 2014 IEEE Global Communications Conference, Austin, TX, 3784-3789.
- 14. Dighe, P.A., Mallik, R.K. and Jamuar, S.S. (2003) Analysis of Transmit-Receive Diversity in Rayleigh Fading. IEEE Transactions on Communications, 51, 694-703. https://doi.org/10.1109/TCOMM.2003.810871
- 15. Hamdi, K. (2008) Capacity of MRC on Correlated Rician Fading Channels. IEEE Transactions on Communications, 56, 708-711. https://doi.org/10.1109/TCOMM.2008.060381
- 16. Popovic, B.M. (2010) Efficient DFT of Zadoff-Chu Se-quences. Electronics Letters, 46, 502-503. https://doi.org/10.1049/el.2010.3510
- 17. Jorswieck, E.A. and Boche, H. (2007) Outage Probability in Multiple Antenna Systems. Transactions on Emerging Telecommunications Technologies, 18, 217-233. https://doi.org/10.1002/ett.1135