Hans Journal of Wireless Communications
Vol.
09
No.
06
(
2019
), Article ID:
33689
,
14
pages
10.12677/HJWC.2019.96024
High Precision Soft Clock Synchronization Method Based on TDOA System
Ge Yan, Hongwei Hou, Yifan Luo, Tianhao Fang, Wenjin Wang, Chi Wu
National Mobile Communications Research Laboratory, Southeast University, Nanjing Jiangsu

Received: Dec. 5th, 2019; accepted: Dec. 23rd, 2019; published: Dec. 30th, 2019

ABSTRACT
Based on the clock synchronization problem in TDOA (Time Difference of Arrival) real-time positioning system, a cross-recognition synchronization method is proposed. The soft clock synchronization design of TDOA positioning system is implemented on the DW1000 module provided by Decawave. Considering the transceiver characteristics of the module, only one signal can be transmitted in space at the same time. The method includes the communication protocol between the primary base station, the secondary base station and the user tag. The communication time slots between the modules are arranged to solve the problem of interference. At the same time, the method analyzes the communication process between modules to derive the linear equations that are satisfied between time stamp, clock frequency drift and time axis deviation. The least squares solution is substituted into the TDOA positioning algorithm to complete a clock synchronization and positioning with the user tag. The method proposed in the paper fully considers the requirements of TDOA real-time positioning system, and has the advantages of low delay, simple implementation and easy analysis.
Keywords:Indoor Positioning, TDOA System, Soft Clock Synchronization, Least Squares

基于TDOA系统的高精度软时钟 同步方法
严格,侯宏卫,罗易凡,房天昊,王闻今,吴驰
东南大学移动通信国家重点实验室,江苏 南京

收稿日期:2019年12月5日;录用日期:2019年12月23日;发布日期:2019年12月30日

摘 要
文章基于TDOA (Time Difference of Arrival,到达时间差)实时定位系统中的时钟同步问题,提出了一种交叉互验同步方法,在由Decawave公司提供的DW1000模块上实现TDOA定位系统的软时钟同步设计。考虑到模块的收发特性,同一时刻只能允许一条信号在空间中传输,该方法中包含主基站与从基站和用户标签的通讯协议,对模块之间的通讯时隙进行安排,解决了通讯信号互相干扰的问题。同时,该方法通过对模块间通讯过程进行建模分析,推导出时间戳、时钟频率漂移与时间轴偏差之间满足的线性方程组,将其最小二乘解代入TDOA定位算法,完成一次时钟同步与标签定位。文章提出的方法充分考虑TDOA实时定位系统的需求,具有时延低、实现简单、易于建模分析等优点。
关键词 :室内定位,TDOA系统,软时钟同步,最小二乘法

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
移动定位服务在人们的生活中发挥着越来越重要的作用,如停车场中车辆的定位、医院中患者的定位、火灾现场中受困人员的定位等。其在给人们提供便利的同时,也为定位系统的性能提出了更高的要求。目前,关于移动终端的定位有多种解决方案,包括基于AOA (Angle of Arrival,到达角度)的定位技术 [1] 、基于RSS (Received Signal Strength,接收信号强度)的定位技术等 [2] 、基于TDOA (Time Difference of Arrival,到达时间差)的定位技术 [3] 、基于TOA (Time of Arrival,到达时间)的定位技术 [4]。而在这些解决方案中,基于TDOA的定位技术从实时性、准确性、低功耗性等多方面满足了定位服务的需求,此外,其易于操作,无需对移动终端提出要求,可直接向用户提供定位服务,这一系列优点使TDOA实时定位算法得到了广泛应用。
对于TDOA实时定位系统,基站间的时钟差异会显著影响信号到达时间差的测量,从而影响最终的定位效果。而在实际情况中,由于晶振老化程度、频率特性、温度等因素的不同,不同芯片的时钟频率会产生漂移。并且,芯片上电时间的差异导致芯片内部时间戳计数器的起始点不同,从而使绝对时间轴产生偏差。时钟频率的漂移和时间轴的偏差将会使TDOA实时定位系统解算出的坐标出现错误。所以,需要提出一种可应用于TDOA实时定位系统的时钟同步方法。
最初的时钟同步系统 [5] 为硬布线式结构,包括同步信号和时钟频率生成器,同步信号与基站模块的引脚连接,可强制将片内系统时钟计数器复位为零,使得不同基站间的时间轴差异问题得以解决。而时钟频率生成端为所有基站芯片提供频率一致的时钟,从而防止不同基站模块晶振由于自身老化或周围环境等原因产生的频率漂移。在硬时钟同步系统中,不同基站之间依然会因为中央频率和同步信号的传输过程产生误差,造成时间轴的差异和时钟频率的漂移,并且布线成本高,对系统架构要求严格,不利于实际系统的部署。因此,适用于实际系统的软时钟同步设计引起了研究人员的广泛关注。
在过去的研究中,针对无线网络中的软时钟同步提出了许多方法。其中,可以按照系统是否具有一定拓扑结构将方法分为两类。具有一定拓扑结构的时钟同步方法如 [6] [7],其时钟同步复杂度低,但对同步过程中的错误较为敏感,易产生错误传播。针对此问题,论文 [8] 提出了一种基于对同步信息的周期性泛洪传播和隐式动态拓扑更新完成时钟同步过程的方法,对链路间的时钟同步过程错误有较强适应性。
其它时钟同步方法没有拓扑结构,主要通过多基站间的信息交换完成时钟同步过程。对于同步过程的优化可以按照信息交换协议与参数估计方法进行分类。论文 [9] [10] [11] 均在基站网络中选取一个主基站作为参考基站,该基站周期性地向其它基站发送时钟同步信息或时钟数据校验包,而其它接收基站则根据接收信息完成时钟同步。论文 [12] [13] 则根据基站间的信息交换构建网络全局虚拟主时钟,所有基站的时钟均与全局虚拟主时钟进行同步,其中,论文 [13] 使用自然选择粒子群算法对网络间基站的信息交换进行数据自适应融合,提高全局虚拟主时钟的精度,进而改善时钟同步精度。除此之外,论文 [14] 选取网络中的两个基站作为主基站,主基站之间完成时钟同步信息的交换,而其它基站则通过监听主基站之间的信息交换实现时钟同步。
除信息交换协议外,对时间轴偏差量与时钟频率漂移量的估计方法也影响着系统的性能。论文 [10] [14] [15] 提出了基于极大似然法的参数估计方法,通过基站之间交换的信息解算时间轴偏差量与时钟频率漂移量的极大似然估计解。论文 [11] [13] [16] [17] 则提出了存在测量误差与同步误差场景下基于卡尔曼滤波器的参数估计方法,对实际系统中的误差和噪声表现进行了优化。此外,论文 [18] 将时钟同步问题转化为控制系统问题,通过基于比例积分法的凸优化建立了线性时钟同步机制。
考虑到时钟同步系统对个别基站时间信息的容错性,论文 [7] [12] [15] [19] [20] 提出了分布式时钟同步方法,并通过共识算法完成最终的时钟同步。特别地,论文 [7] 使用JEGA (Joint estimation and gossip-averaging algorithm,联合估计与传播平均算法)对抗同步过程中的噪声,论文 [19] 则采取两个共识算法的级联完成本地信息的平均。
现有的软时钟同步方法对基站端的算法复杂度要求较高,且有些方法要求基站端有较高的功率和较强的并行处理能力,不适用于低成本系统的架构。并且,这些方法中的时钟同步过程与TDOA定位过程冲突,必须交替进行,无法做到实时同步,导致最终定位效果受到影响。针对现有方法存在的问题,本文提出了一种交叉互验时钟同步方法,可在TDOA定位的过程中实现软时钟同步。该方法通过定义基站间的通讯协议,对模块之间的通讯时隙进行安排,解决了通讯信号互相干扰的问题。同时,通过对模块间通讯过程进行建模分析,推导出时间戳、时钟频率漂移与时间轴偏差之间满足的线性方程组,将其最小二乘解代入TDOA定位算法,完成一次时钟同步与标签定位。本文提出的方法在时钟同步的过程中同步完成TDOA定位,解决了前述的“伪同步”问题,并且具有计算复杂度低、易于建模分析等优点,在TDOA实时定位系统中也表现出较优的性能。
2. TDOA定位
TDOA定位原理
实时定位系统通常由一系列已知坐标的基站和一个未知坐标的用户标签组成,TDOA定位通过测量信号飞行时间差估计用户标签与不同基站之间的距离差,从而解算用户标签的坐标 [21]。
定义 为用户标签的坐标, 为基站坐标,其中N为基站数。则用户标签与基站之间信号飞行的真实时间可表示为
(1)
其中,c为光速。
考虑到噪声的影响,在实际系统中用户标签与基站之间信号飞行时间的测量值为
(2)
其中, 表示服从高斯分布的测量噪声,即 。从而,用户标签与第i个基站和第j个基站距离差的测量值可由下式给出
(3)
在TDOA定位过程中,选取基站1作为参考主基站,并且测量用户标签与其它基站和参考主基站之间的距离差。重写公式(1),我们可以得到
(4)
其中 。同时,我们有
(5)
根据公式(4)和公式(5),我们可以得到以下等式
(6)
由于测量过程中不可避免的噪声,定义 ,则公式(6)的误差向量可以表示为
(7)
其中
极大似然估计基于误差向量的协方差进行计算
(8)
其中,协方差矩阵 ,且 。由于协方差矩阵中包含用户标签与基站之间的真实距离,所以我们需要进行迭代求解,从而解算满足一定精确度的估计值。首先,定义 ,并且在第一轮迭代中假定 ,则公式(8)可化简为
(9)
根据公式(9)估计的 计算矩阵
的近似解,并重新带回公式(8),即可求得迭代解。但是只经过一次极大似然估计的值无法满足精确度要求,因此需要进行进一步优化。
计算矩阵
的近似解,并重新带回公式(8),即可求得迭代解。但是只经过一次极大似然估计的值无法满足精确度要求,因此需要进行进一步优化。
定义 ,则 与第一次极大似然估计值 之间的误差向量可以表示为
(10)
其中,
根据极大似然法原理, 的估计解为
(11)
其中,协方差矩阵 。
最终,用户标签的坐标可以表示为 。
3. 交叉验证的时钟同步
3.1. 时钟误差模型
考虑两个基站间的单收单发过程,进而建立时钟误差模型(图1)。
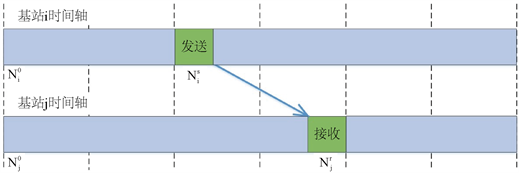
Figure 1. Schematic diagram of single transceiver communication process
图1. 单次收发通讯过程示意图
假定在初始时刻,基站i和基站j的时间戳寄存器值分别为 和 ,则在经过时间t后,时间戳寄存器的值满足
(12)
(13)
其中, 和 分别为基站i和基站j的实际时钟频率,一般情况下,由于芯片晶振的抖动误差, ,从而产生了时钟频率漂移问题。
对于距初始时刻时间t后的一次发送过程,基站 记录下的发送时间戳 与基站j记录下的接收时间戳 满足如下关系
(14)
(15)
其中, 为基站i和基站j之间的距离,c为光速(即信号在空间中传播速度), 为发送与接收时延。为简化分析,假设所有模块的收发时延均相同。
整理后可得
(16)
(17)
其中, 定义为基站i和基站j之间的时钟偏移量。
3.2. 时钟同步过程
根据模块手册,我们可以发现模块在处理完接收到的信号之前,会拒绝其它信号的接收,即同一时间内模块只能接收并处理一条信号。同时,由于模块中的天线为半双工工作模式,模块在某一时刻只能发送一条信号或接收一条信号,无法同时进行。模块的收发特性限制了工作效率,如果按照常用思路进行同步,每个时隙都有绝大多数的模块处于闲置状态,并且时钟同步过程与TDOA定位过程需要设计不同的协议,增加了协议设计的复杂度。此外,若基站数目继续增长,每次时钟同步的周期过长,导致在此时间内用户标签产生了较大的位置变动,影响定位精度。
基于以上特性,交叉互验的时钟同步方法如下。
此方法将时钟同步过程与TDOA定位过程作为整体,每个完整的工作周期包括三种通信任务类型:激活信号、TDOA信号、反馈信号。激活信号由主基站发送,标志一个工作周期的开始,主基站发送激活信号后进入全接收状态。用户标签接收到主基站发送的激活信号后,开始向所有基站发送TDOA信号,此后进入全接收状态,在接收到下一个激活信号之前不对接收到的信号进行任何处理。从基站在接收到主基站发送的激活信号后,等待用户标签发送的TDOA信号,此后进入休眠状态,并按照激活信号中的指令逐一醒来,向主基站和其它未处于休眠状态的从基站发送反馈信号,其数据包中包含TDOA信息与时钟同步信息。
该方法的时序逻辑如图2所示。
在本方法中,主基站决定了整个系统的工作时序,该决定作用主要表现在激活信号的数据包中包含了各个从基站的休眠时长、反馈信号数目及目的地等信息,各从基站在接收到激活信号的数据包后按照其指示开始后续工作,完成整个系统的时钟同步与标签定位功能。
在这种设计下,模块间的丢包情况可以分为两种情况。若丢失了一条从基站之间的反馈信号,根据方法设计,线性方程组的系数矩阵冗余,即方程数目大于未知数数目,所以从基站之间反馈信号的丢包对于结果不产生明显影响。但若从基站丢失了主基站的激活信号,或主基站丢失了最后一个从基站发送的反馈信号,则会使主基站在一次激活信号发送后一直处于全接收状态,造成时序混乱。为此,该方法为主基站设置了接收超时处理机制,将根据理想中的时序安排设定超时时限,若主基站接收超时,则抛弃本轮工作周期接收到的所有信号,重置相关状态,立即进入下一工作周期。由于设计的超时时限将大于工作周期时长,在主基站接收超时后,从基站和用户标签均已处于初始状态,可以直接进入下一工作周期。

Figure 2. Temporal logic
图2. 时序逻辑
3.3. 通信协议设计
该方法与过去软时钟同步的基本思路不同,充分利用了模块的收发特性,提高了整个工作周期的效率。而与此同时,模块间的通讯过程也相较于基本思路复杂了许多。所以,模块间的通讯协议设计就显得尤为重要。
该方法中的通讯协议中主要包含信号基本信息、定位数据与同步数据三部分,其中信号基本信息部分包括本条信号发送模块编号、信号接收模块编号、信号类型、从基站延迟时长及信号发送时间戳;定位数据包括从基站接收到TDOA信号的时间戳,由从基站反馈得到;同步数据则包括方法中反馈信号的发送模块编号、接收模块编号、发送与接收时间戳等信息,用于整个系统的时钟同步。协议所需寄存器的大小与位数视系统大小而定,协议整体内容如图3所示。
其中,协议各字段的说明如表1所述。
每个模块拥有自己的编号,其编号方式需要区分用户标签与定位基站,协议中模块编号字段的长度限制了用户标签和基站个数存在的上限,在系统的实际用户数目超过此上限时,协议字段的长度需要重新设计。在设置接收模块编号时,包括四种接收模式:将全部用户标签作为接收模块、将全部基站作为接收模块、将全部模块作为接收模块、将指定基站作为接收模块。
结合上述通讯协议,本方法可具体描述如下:
主基站将数据包中Rx_Buffer[1]设定为将全部模块作为接收模块,并在Rx_Buffer[2]中设定信号类型为激活信号,同时,为安排整个系统给的工作时序,在Rx_Buffer[3]中设定从基站发送反馈信号的延时时长,最后发送激活信号。
用户标签接收到主基站发送的信号后,从接收信号的Rx_Buffer[2]位读取信号类型,确认为激活信号后,在本地数据包的Rx_Buffer[1]设定为将全部基站作为接收模块,并在Rx_Buffer[2]中设定信号类型为TDOA信号后发送此信号。
从基站在接收到用户的TDOA信号后,将自身的接收时间戳写入数据包的Rx_Buffer[8:11],同时,将本地数据包的Rx_Buffer[1]设定为将全部基站作为接收模块,并在Rx_Buffer[2]中设定信号类型为反馈信号,最后,发送此信号。除此之外,从基站在接收到其它从基站发送的反馈信号后,读取该信号中的发送模块编号与发送时间戳,将本地的接收模块编号与接收时间戳一同写入自身反馈信号数据包,作为时钟同步数据。并且,每当从基站接收到其它从基站发送的反馈信号并记录时,将自身反馈信号数据包中的Rx_Buffer[12]数据增加1,使得最后时钟同步的主基站可以明确数据包中有效数据的数目。
通讯协议中,发送模块编号、接收模块编号、信号类型、信号发送时间戳均由发送模块在发送前完成设定,供接收模块进行相关数据的提取。
需要注意的是,在DW1000芯片中,发送时间戳定义为数据帧内的PHR段被发送的时刻对应的时间戳。因此,只有将信号已经封装好并进行发送之后才能确定本次发送的发送时间戳。也就是说,通讯协议中的信号发送时间戳均为此模块上一次信号的发送时间戳,在实际的数据处理过程中需要进行调整。
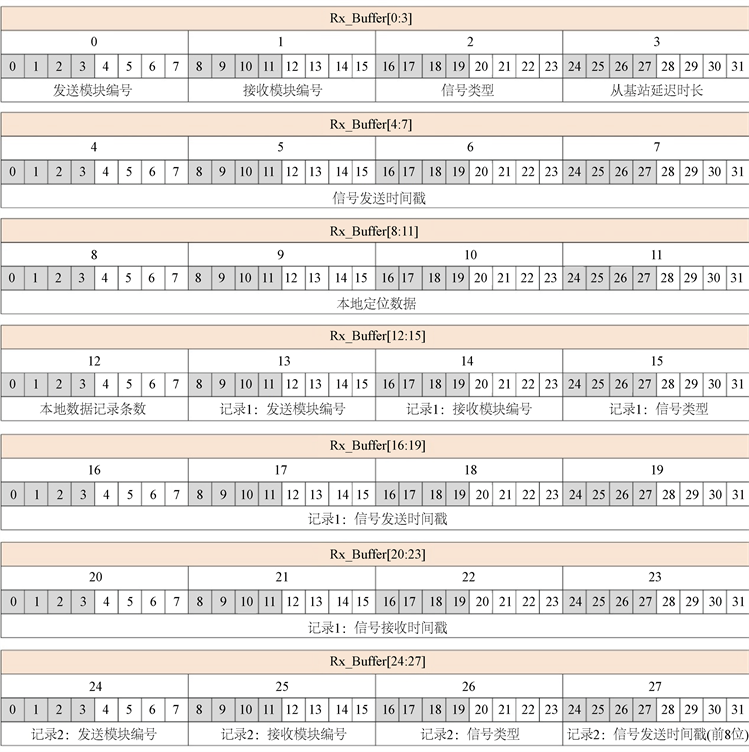
Figure 3. Communication protocol
图3. 通讯协议
Table 1. Description of the protocol field
表1. 协议字段说明
3.4. LS同步
考虑完整的时钟同步方法设计,主基站与其它所有从基站均进行过两次单收单发通讯(激活信号、反馈信号),产生2n条独立方程,其中n为从基站个数。第i个从基站与其它未处于休眠状态的从基站发送反馈信号,此时未处于休眠状态中的从基站数目为 个,即产生 条独立方程。所以,每个工作周期产生的独立方程总数为
(18)
由于时钟频率漂移的影响,每个模块的时钟频率均有差异,即时钟频率产生了 个独立未知量。同时注意到 ,即偏移量仅产生n个独立未知量。由于在模型中,我们假设所有模块的收发时延均相同,所以收发时延产生1个独立未知量。综上所述,独立未知量的个数为
(19)
若要在一个工作周期内计算出全部的独立未知量,则要求 ,解得
n ≥ 3,即至少需要3个从基站。在TDOA定位系统中,若要解算得到用户标签的三维坐标,也至少需要3个从基站。由此可见,该方法可以很好的应用到TDOA实时定位系统中。
,解得
n ≥ 3,即至少需要3个从基站。在TDOA定位系统中,若要解算得到用户标签的三维坐标,也至少需要3个从基站。由此可见,该方法可以很好的应用到TDOA实时定位系统中。
将线性方程组表示为矩阵形式
(20)
其中,矩阵 的行向量 表示基站i和基站j之间的一次单收单发的通讯过程,向量 则表示与矩阵 的行向量对应的通讯基站间的物理距离。
(21)
(22)
该线性方程组的最小二乘解为
(23)
结合用户标签向所有基站发送的TDOA信号过程,可以发现接收TDOA信号的真实时间差满足 ,其中, 和 分别为基站i和基站j接收到TDOA信号的真实时间。基于公式(12)和(13),我们可以得到
(24)
由于 ,因此我们只需要得到 ,根据公式(24),有
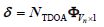 (25)
(25)
其中,与式(21)类似,矩阵 的行向量 表示主基站和基站i收发TDOA信号过程的系数向量
(26)
至此,可以将交叉互验同步方法描述如下。
在每一轮工作周期结束后,通过式(23)解算出时钟同步向量 ,将解算到的时钟同步向量代入式(25),得到各基站接收到TDOA信号的真实时间差向量,最终将真实时间差向量代入前述TDOA算法,解算用户标签的三维坐标。
4. 基于实测数据的仿真验证
4.1. 实物测量
前述部分介绍了一种基于TDOA实时定位系统的软时钟同步方法,现将软时钟同步过程与TDOA定位过程进行整合,并确定系统相关参数,从而对整个系统进行仿真,验证整体方法的可行性。
4.1.1. 定位模块
实际系统中使用Decawave公司生产的DW1000模块作为TDOA定位模块。DW1000是一款高度集成的低功耗CMOS无线收发芯片,其符合IEEE 802.15.4-2011 UWB(Ultra-wideband,超宽带)标准。芯片的主要功能包括发送和接收指定帧格式的无线电信号,并从接受信号中分析信号质量。
芯片内置多种发送与接收方式,均可由使用者自行设定,极大满足了不同系统中相关设定的灵活性与可控性。同时,其设计了可用于监听信号的嗅探模式,在监听信号的同时保证低功耗要求。此外,该芯片成本低廉,可用于实时定位系统的大规模部署 [22]。
4.1.2. 可行性分析
首先,在此方法中,模块在不同收发信号间隔下的丢包率对于工作周期的长度而言尤为重要。若满足丢包率限制的发送频率过低,会导致工作周期过长,用户标签在此周期内的位置变动较大,对系统的精确度和实用性造成影响。
为确定合适的发送频率,对不同发送频率下的丢包率进行测试,结果见表2。
Table 2. Relationship between sending frequency and packet loss rate
表2. 发送频率与丢包率关系
由测试数据可见,当发送频率在200 Hz以下时,丢包率均不大于0.05%,对实际系统的影响可以忽略不计,故系统中发送频率的配置一般设置为200 Hz及以下。
此外,还需要验证模块设置是否能支持本文提出的方法。考虑系统中存在1个主基站和n个从基站的情况。设每次通信发送的数据中,前B个字节用于描述本次通信的信息,本地记录的通信记录共R条,每一条占用L个字节。每次发送的数据量最大为M字节,则有
(27)
根据图3中的通讯协议,前13个字节为每一次信号发送均需要的固定字节长度(Rx_Buffer[0:12]),即 ,且每条记录长度 。而n个从基站中获得其它从基站反馈信号最多的从基站拥有 条时钟同步信号的记录,所以 。同时,每次发送数据包最大的数据承载量为127字节 [23],即 。将上述参数的值代入式(27)可知 。根据论文 [21],解算出用户标签三维坐标的系统至少需要1个主基站和3个从基站,即最终实际系统中的从基站数目n需要满足 。
4.1.3. 噪声测量分析
在实际系统中,模块之间的收发过程存在一定的随机噪声,从而影响时钟同步与实时定位的准确性。因此,为确定随机噪声对实际系统性能的影响,需要对噪声情况进行测量。为简化测量,假定随机噪声对于所有模块的组合均服从相同分布。
将一组DW1000模块置于固定点进行多次单收单发测试,提取每次单收单发过程的时间戳信息进行分析,将接收时间戳与发送时间戳的差值进行归一化后绘制累计概率分布曲线,并与标准高斯分布进行比较。可以发现,随机噪声服从高斯分布,并且其噪声标准差约为7000时间戳单位(最大时间戳约为4.29 × 109)。
4.2. 仿真设置
简单而不失一般性,可以通过计算机仿真对应用时钟同步方法的TDOA实时定位系统进行性能分析,且仿真过程相关参数的选取基于前述对实际系统的测量。
为防止丢包率对系统性能产生较大影响,根据表2的结果,选取信号发送频率为200 Hz;同时,考虑到对系统部署复杂度与定位算法效果的权衡,仿真过程中的系统包含1个主基站与5个从基站。根据论文 [21],TDOA定位算法要求基站不处于同一平面,且尽可能分散。
因此,根据上述考虑,仿真相关参数设置见表3。
Table 3. Simulation parameter setting
表3. 仿真参数设置
在实际系统的设计与计算机仿真过程中,为降低随机噪声对系统性能的影响,采用对数据取平均的方法降低其影响。本次仿真取36000次数据进行平均,对应实际系统约为30分钟。
4.3. 仿真结果与分析
图4显示的是用上述同步方法矫正后的各基站同步参数 各元素的累积误差分布曲线。从图中可以看出,90%分位点的误差均在6 cm以内,这样的误差对于TDOA算法来说是可以容忍的。
将矫正后的TDOA数据 代入TDOA算法,解得定位结果,并与真实坐标对比,计算定位误差的累积分布,可以得到图5中的曲线。从图中可以看出,10000次定位结果的定位误差不超过20 cm。结果说明时钟互验同步方法在TDOA定位系统中的时钟同步和实时定位精度方面均有显著提高。
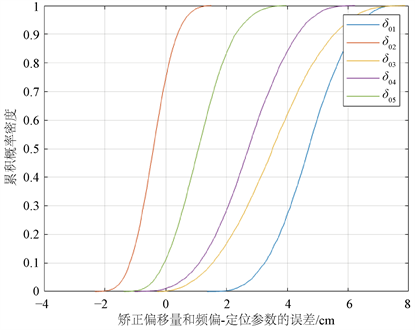
Figure 4. Cumulative probability distribution curve of synchronization parameter error
图4. 同步参数误差累计概率分布曲线
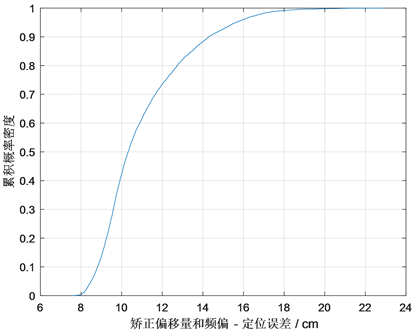
Figure 5. Cumulative probability distribution curve of TDOA positioning errors
图5. TDOA定位误差累计分布曲线
5. 结论
本文提出了一种可应用于TDOA实时定位系统的交叉互验同步方法,该方法充分利用模块收发特性,在时钟同步的过程中完成TDOA定位,从而提升了工作效率和定位精度。同时,本文通过对整体方法的数学建模分析,将复杂的同步算法与定位算法简化为基本矩阵运算,具有运算简单、易于实现、可与定位同步进行等优点。此外,该方法考虑到了现有时钟同步方法中存在未利用的冗余信号问题,通过最小二乘法将所有冗余信号加以利用,通过最小化定位误差的平方和寻找最佳定位结果,在仿真分析中可以得到较优的性能。
文章引用
严 格,侯宏卫,罗易凡,房天昊,王闻今,吴 驰. 基于TDOA系统的高精度软时钟同步方法
High Precision Soft Clock Synchronization Method Based on TDOA System[J]. 无线通信, 2019, 09(06): 185-198. https://doi.org/10.12677/HJWC.2019.96024
参考文献
- 1. Bergen, M.H., Jin, X., Guerrero, D., Chaves, H.A.L.F., Fredeen, N.V. and Holzman, J.F. (2017) Design and Implementation of an Optical Receiver for Angle-of-Arrival-Based Positioning. Journal of Lightwave Technology, 35, 3877-3885.
https://doi.org/10.1109/JLT.2017.2723978 - 2. Cui, W., Zhang, L., Li, B., Guo, J., Meng, W., Wang, H. and Xie, L. (2018) Received Signal Strength Based Indoor Positioning Using a Random Vector Functional Link Network. IEEE Transactions on Industrial Informatics, 14, 1846-1855.
https://doi.org/10.1109/TII.2017.2760915 - 3. Yuan, Y., Hou, S. and Zhao, Q. (2017) An Improved TDOA Localization Algorithm Based on Wavelet Transform. 2017 7th IEEE International Conference on Electronics Information and Emergency Communication (ICEIEC), Macau, 21-23 July 2017, 111-114.
https://doi.org/10.1109/ICEIEC.2017.8076523 - 4. Xu, A.Y.Z., Au, E.K.S., Wong, A.K.S. and Wang, Q. (2009) A Novel Threshold-Based Coherent TOA Estimation for IR-UWB Systems. IEEE Transactions on Vehicular Technology, 58, 4675-4681.
https://doi.org/10.1109/TVT.2009.2020990 - 5. DecaWave (2014) Wired Synchronization of Anchor Nodes in A TDOA Real Time Location System.
- 6. 刘克难. CTC时钟同步方案研究与设计[J]. 铁路通信信号工程技术, 2018(6): 39-43.
- 7. Marechal, N., Pierrot, J.-B. and Gorce, J.-M. (2008) Fine Synchronization for Wireless Sensor Networks Using Gossip Averaging Algorithms. 2008 IEEE International Conference on Communications, Beijing, China, 19-23 May 2008, 4963-4967.
- 8. Maróti, M., Kusy, B., Simon, G., et al. (2004) The Flooding Time Synchronization Protocol. Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems, Baltimore, MD, 3-5 November 2004, 39-49.
https://doi.org/10.1145/1031495.1031501 - 9. Elson, J., Girod, L. and Estrin, D. (2002) Fine-Grained Network Time Synchronization Using Reference Broadcasts. ACM SIGOPS Operating Systems Review, 36, 147-163.
https://doi.org/10.1145/844128.844143 - 10. 陈辉. 基于TDOA的无线传感器网络时钟同步与定位技术研究[D]: [硕士学位论文]. 长沙: 国防科学技术大学, 2015.
- 11. 罗勃, 沈重, 朱雨豪. 无线时钟同步算法在UWB定位技术中的研究与应用[J]. 现代电子技术, 2017, 40(6): 31-34+39.
- 12. Liao, C. and Barooah, P. (2014) Accurate Distributed Time Synchronization in Mobile Wireless Sensor Networks from Noisy Difference Measurements. arXiv preprint arXiv:1412.7888.
- 13. 蒋伊琳, 张芳园. 基于自然选择粒子群的时钟同步算法[J]. 西南交通大学学报, 2017, 52(3): 593-599.
- 14. Qaraqe, K., Chaudhari, Q.M. and Serpedin, E. (2010) Some Improved and Generalized Estimation Schemes for Clock Synchronization of Listening Nodes in Wireless Sensor Networks. IEEE Transactions on Communications, 58, 63-67. ttps://doi.org/10.1109/TCOMM.2010.01.080226
- 15. Solis, R., Borkar, V.S. and Kumar, P.R. (2006) A New Distributed Time Synchronization Protocol for Multihop Wireless Networks. IEEE Conference on Decision and Control (CDC), San Diego, CA, 13-15 December 2006, 2734-2739.
https://doi.org/10.1109/CDC.2006.377675 - 16. 游路瑶, 黄庆卿, 段斯静. 基于卡尔曼滤波估计的一致性时钟同步算法[J]. 计算机应用, 2017, 37(8): 2177-2183.
- 17. Freris, N.M., Borkar, V.S. and Kumar, P.R. (2009) A Model-Based Approach to Clock Synchronization. Proceedings of the 48th IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, 15-18 December 2009, 5744-5749.
https://doi.org/10.1109/CDC.2009.5399516 - 18. Carli, R., Chiuso, A., Schenato, L. and Zampieri, S. (2008) A PI Consensus Controller for Networked Clocks Synchronization. Proceedings of the 17th World Congress The International Federation of Automatic Control, Seoul, Korea, 6-11 July 2008, 10289-10294.
- 19. Schenato, L. and Fiorentin, F. (2011) Average Time Synch: A Consensus-Based Protocol for Clock Synchronization in Wireless Sensor Networks. Automatica, 47, 1878-1886.
https://doi.org/10.1016/j.automatica.2011.06.012 - 20. Carli, R. and Zampieri, S. (2014) Network Clock Synchronization Based on the Second-Order Linear Consensus Algorithm. IEEE Transactions on Automatic Control, 59, 409-422.
https://doi.org/10.1109/TAC.2013.2283742 - 21. Wu, C., Hou, H., Wang, W., Huang, Q. and Gao, X. (2018) TDOA Based Indoor Positioning with NLOS Identification by Machine Learning. 2018 10th International Conference on Wireless Communications and Signal Processing, Hangzhou, 18-20 October 2018, 1-6.
https://doi.org/10.1109/WCSP.2018.8555654 - 22. Decawave (2015) DW1000 Datasheet.
- 23. Decawave (2017) DW1000 User Manual.
