Advances in Geosciences
Vol.
12
No.
12
(
2022
), Article ID:
59274
,
9
pages
10.12677/AG.2022.1212153
基于有限差分法的射频大地电磁二维正演模拟
张艺冰1,童孝忠1,2*,钱文圣1
1中南大学地球科学与信息物理学院,湖南 长沙
2中南大学“有色资源与地质灾害探查”湖南省重点实验室,湖南 长沙
收稿日期:2022年11月7日;录用日期:2022年12月7日;发布日期:2022年12月20日

摘要
在大多数二维地电模型中,考虑到射频大地电磁响应不存在解析解,本文建立了均匀网格有限差分正演模拟算法。首先,从电磁场满足的变系数亥姆霍兹方程边值问题出发,导出了有限差分法控制方程的离散表达式,并对边界条件近似处理后求解线性方程组得到射频大地电磁场数值解。其次,对均匀半空间模型进行模拟计算,且与解析法计算结果对比,验证了射频大地电磁有限差分正演算法的正确性和稳定性。最后,模拟计算了射频大地电磁典型二维地电模型的响应,总结了异常响应规律,为实测数据的定性解释提供指导。
关键词
射频大地电磁,二维,正演模拟,有限差分法,均匀网格

Forward Modeling for Two-Dimensional Radio-Magnetotelluric Based on Finite Difference Method
Yibing Zhang1, Xiaozhong Tong1,2*, Wensheng Qian1
1School of Geosciences and Info-Physics, Central South University, Changsha Hunan
2Key Laboratory of Non-Ferrous Resource and Geological of Hunan Province, Central South University, Changsha Hunan
Received: Nov. 7th, 2022; accepted: Dec. 7th, 2022; published: Dec. 20th, 2022

ABSTRACT
In the most two-dimensional geo-electric model, there are no analytical solutions for radio-magnetotelluric responses, so the uniform-meshes finite difference algorithm was developed for numerical results in this paper. Firstly, from the boundary value problem of variable coefficient Helmholtz equation for electric field and magnetic field, the discrete expressions of governing equation are derived from finite difference method. The numerical solutions of electric field and magnetic field are calculated after the approximate treatment on the boundary conditions. Secondly, through the simulation of homogeneous half-space model and compared with the analytical results, the correctness and stability of the finite difference forward algorithm are verified. Lastly, by the numerical simulation for a two-dimensional model, radio-magnetotelluric responses were summarized, which can provide for qualitative interpretation of field data.
Keywords:Radio-Magnetotelluric, Two-Dimensional/2D, Forward Modeling, Finite Difference Method, Uniform Meshes

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
射频大地电磁(Radio-magnetotelluric,简称RMT)是新兴的浅地表地球物理勘探方法,其工作频段(10 kHz~1 MHz)处于音频大地电磁(Audio-frequency magnetotelluric,简称AMT)与探地雷达(Ground-penetrating radar,简称GPR)之间 [1]。相较于音频大地电磁测深,射频大地电磁测深对百米内的地下介质具有更好的分辨率,在地质灾害预警预报、环境工程勘察 [2] [3] 和地质构造勘探等领域有着广泛应用 [4] [5]。
为了利用射频大地电磁勘探方法查明地下构造及岩体的空间展布特征,需要将电磁信号转换为勘探地质体所对应的电性变化,其中包含了实测数据预处理、反演成像、定性定量解释。射频大地电磁正反演解释的前提是电磁信号因地质体的电性变化而产生差异,故可根据实测数据和实际需要开展针对性的一维、二维和三维地电模型的正反演解释。对于射频大地电磁法,我们通常会用有限单元法和有限差分法对二维地电模型数值模拟,三维模型用积分方程法,当前,射频大地电磁勘探方法的一维、二维正反演技术是实际资料处理和解释的主要技术手段 [6] [7]。有限差分法(Finite difference method)作为一种经典的数值模拟方法,其数值计算的基本原理是采用差商来代替微商或偏微商,将偏微分方程定解问题转变为适定的线性方程组来求解,具有直观、无需构建形函数、不存在单元分析和整体分析的优点,其数学建模简便,易于编程,易于并行。这能为地下电性结构提供良好的近似 [8] [9] [10] [11] [12]。因此在本文中,我们选用有限差分法来实现射频大地电磁二维正演模拟。
本文从大地电磁场所满足的变系数亥姆霍兹方程边值问题出发,建立了射频大地电磁二维正演模拟的均匀网格型有限差分算法,这为后续的射频大地电磁二维反演计算提供了数值计算工具。通过试算存在解析解的均匀半空间地电模型,验证了有限差分正演算法的准确性和稳定性。利用有限差分数值算法进一步计算了典型二维地电模型的射频大地电磁响应,分析了勘探方法的异常响应特点,可以定性判别出异常体构造的电阻率分布特征和空间展布特征,这能为实测数据的定性解释提供指导作用。
2. 边值问题
对于二维地电模型,若地下介质的电性参数沿走向x不发生变化,即 ,即 和 。这时,电场 与磁场 满足的变系数亥姆霍兹方程分别为 [13]:
(1)
(2)
式中, 为角频率,且 (f为频率); 为介质的电导率(电阻率的倒数),其单位为S/m,空气中的电导率取为 ; 为磁导率,其单位为H/m,真空中的磁导率取为4π × 10−7 H/m; 为介质的介电常数,其单位为F/m,真空中的介电常数取为8.85 × 10−12 F/m。
式(1)和式(2)可统一表示成
(3)
对于TE极化模式,有
,, (4)
而对于TM极化模式,有
,, (5)
为了求解变系数亥姆霍兹方程,还必须给出相应的边界条件(见图1),进而得到射频大地电磁二维正演计算的边值问题。
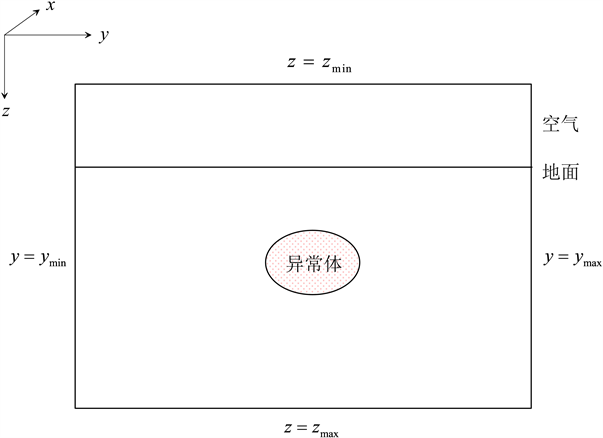
Figure 1. Schematic diagram of boundary conditions for 2D radio-magnetotelluric forward modeling
图1. 射频大地电磁二维正演计算的边界示意图
下面,给出射频大地电磁二维正演计算的边界条件:
1) 矩形计算区域的上边界条件为第一类非齐次边界,取 离地面足够远的空气中(TE与TM极化模式均要空气层),使异常体产生的场在此边界上为零,通过归一化处理后可取该边界处的场值为常数1,即
(6)
2) 矩形计算区域的下边界 为第三类齐次边界条件,即
(7)
这里: , 是 以下岩石的电导率。
3) 矩形计算区域的左、右边界为第二类齐次边界条件,电磁场在 、 上的边界条件可写成
, (8)
3. 有限差分正演算法
3.1. 控制方程离散
采用均匀矩形网格将二维地电模型离散化,如图2所示。下面以求解射频大地电磁的TE极化模式为例,详细推导有限差分正演算法。令
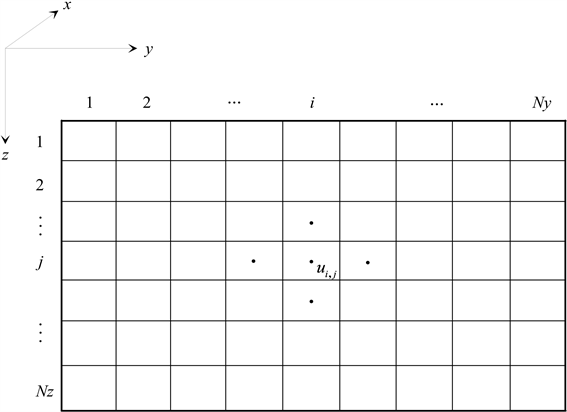
Figure 2. Discretization for 2D geo-electric model with uniform meshes
图2. 二维地电模型非均匀网格离散化
对于研究区域的内部节点,在单元 中心处,采用有限差分近似计算偏导数:
(9)
和
(10)
将式(9)和式(10)代入到式(3),可得
即
(11)
3.2. 边界条件处理
上边界节点为第一类非齐次边界条件,于是有
(12)
下边界节点满足第三类齐次边界条件,则有
(13)
左、右边界节点满足第二类齐次边界条件,可得
(14)
将所有内部节点和边界节点进行有限差分法处理,最终导出射频大地电磁二维正演计算的复系数线性方程组:
(15)
求解该线性方程组即可得到各单元中心处的电场值或磁场值,从而可以进一步计算射频大地电磁的视电阻率和阻抗相位 [14]。
3.3. 射频大地电磁响应计算
当利用有限差分法计算出离散的 值(电场或磁场)后,需要求出辅助场值( ,即 或 ),方能进一步计算射频大地电磁响应(包括视电阻率和阻抗相位) [15]。对于TE极化模式,有
(16)
对于TM极化模式,有
(17)
取近地表的4个等距节点上的u值,利用差商公式将偏导数项转化为代数项,进而实现电场或磁场的偏导数数值计算 [16]:
(18)
这样做提高了射频大地电磁辅助场值的计算精度,其中L是离散节点①至离散节点④的距离。
4. 正演算法测试与模型试算分析
4.1. 算法测试
通过以上对二维射频大地电磁响应均匀网格有限差分法的正演计算,我们使用MATLAB工具编写了计算程序来验证这一算法的正确性和稳定性。首先选用均匀半空间模型,其电导率值为0.0001 S/m、相对介电常数为5,采用均匀网格有限差分法进行计算,取计算区域的横向长度为16 km、纵向宽度为2 km,且横向与纵向剖分网格单元长度分别设置为100 m和10 m。为了显示位移电流的影响,我们选用的频率范围为10 kHz~250 kHz。
图3为TE极化模式下得视电阻率和相位响应,一维解析解与二维有限差分数值解曲线吻合,视电阻率平均相对误差为0.02%,相位平均相对误差为0.01%,这说明本文建立的二维正演算法在模拟精度上可以满足实用要求。当频率超过30 kHz后,由于位移电流的影响视电阻率值大幅度下降,而相位则从10 kHz开始就明显下降。
 (a) 视电阻率曲线(b) 相位曲线
(a) 视电阻率曲线(b) 相位曲线
Figure 3. Comparison of 2D Finite difference solution with 1D analytical solution for a homogeneous half-space model
图3. 均匀半空间模型的二维有限差分解与一维解析解对比
4.2. 二维模型试算分析
构造的二维地电模型如图4所示,在电阻率为10000 Ω∙m的围岩中,存在电阻率为1000 Ω∙m的低阻异常体,且异常体的相对介电常数取为5,异常体距离顶部20 m。
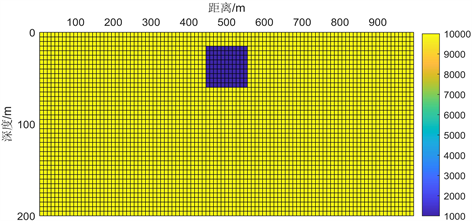
Figure 4. Asimple 2D geo-electric model
图4. 简单二维地电构造模型
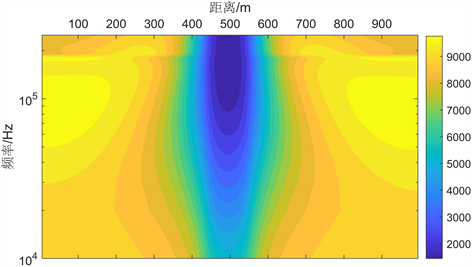 (a) 频率–视电阻率拟断面图
(a) 频率–视电阻率拟断面图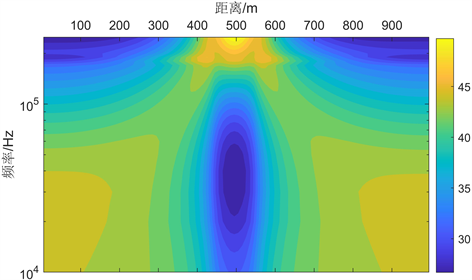 (b) 频率–相位拟断面图
(b) 频率–相位拟断面图
Figure 5. Pseudo-section map of radio-magnetotelluric responses for a simple 2D model in TE mode
图5. TE极化模式下简单二维模型的射频大地电磁响应拟断面图
采用有限差分法计算TE极化模式的射频大地电磁响应,横向左右边界外延1000 m,横向网格单元取 ,纵向网格单元分别取 。模拟测点数设置为100个(点距10 m),选用80个记录频点(10~250 kHz)。图5给出了TE极化模式下二维模型的有限差分数值模拟结果(包括视电阻率和阻抗相位曲线),通过定性分析可以从拟断面图判别出异常体构造的分布位置以及大概的电阻率值。
5. 结语
1) 从射频大地电磁场所满足的变系数亥姆霍兹方程定解问题出发,详细推导了二维正演数值模拟的均匀网格型有限差分算法。采用有限差分格式,实现了偏微分方程转化为代数方程,再通过第一类非齐次边界、第二类齐次边界和第三类齐次边界的差分近似处理,导出了射频大地电磁正演计算的复系数线性方程组,并编写了有限差分正演计算程序。
2) 通过模拟计算均匀半空间模型结果与理论解析结果对比,验证了射频大地电磁均匀网格有限差分正演算法的准确性。本文考虑到位移电流的影响,射频大地电磁的视电阻率值和相位值在高频段会出现大幅度下降,在数值模拟过程中,本文构建的模型在频率超过30 kHz后,视电阻率值大幅下降,相位从10 kHz开始就明显下降。
3) 通过计算TE极化模式下简单二维地电模型的视电阻率和阻抗相位响应,验证了均匀网格有限差分正演算法的有效性,同时定性分析了二维模型的射频大地电磁响应。本文建立的有限差分正演算法不仅能对目前射频大地电磁数值模拟形成有益补充,提高资料处理和解释水平,而且由于方法的通用性,对于类似地球物理正演问题具有同样的实用价值。
文章引用
张艺冰,童孝忠,钱文圣. 基于有限差分法的射频大地电磁二维正演模拟
Forward Modeling for Two-Dimensional Radio-Magnetotelluric Based on Finite Difference Method[J]. 地球科学前沿, 2022, 12(12): 1577-1585. https://doi.org/10.12677/AG.2022.1212153
参考文献
- 1. Shan, C.L., Bastani, M., Malehmir, A., et al. (2016) Integration of Controlled-Source and Radio-Magnetotellurics, Electric Resistivity Tomography, and Reflection Seismics to Delineate 3D Structures of a Quick-Clay Landslide Site in Southwest of Sweden. Geophysics, 81, 13-29. https://doi.org/10.1190/geo2014-0386.1
- 2. Wang, S.G., Malehmir, A., Bastani, M., et al. (2016) Geophysical Characterization of Areas Prone to Quick-Clay Landslides Using Radio-Magnetotelluric and Seismic Methods. Tectonophysics, 577-578, 248-260. https://doi.org/10.1016/j.tecto.2016.04.020
- 3. Tezkan, B., Hördt, A. and Gobashy, M. (2000) Two-Dimensional Radio-Magnetotelluric Investigation of Industrial and Domestic Waste Sites in Germany. Journal of Applied Geophysics, 44, 237-256. https://doi.org/10.1016/S0926-9851(99)00014-2
- 4. Mehta, S., Bastani, M., Malehmir, A., et al. (2017) Resolution and Sensitivity of Boat-Towed RMT Data to Delineate Fracture Zones—Example of the Stockholm Bypass Multi-Lane Tunnel. Journal of Applied Geophysics, 139, 131-143. https://doi.org/10.1016/j.jappgeo.2017.02.012
- 5. Linde, N. and Pedersen, L.B. (2004) Characterization of a Fractured Granite Using Radio Magnetotelluric (RMT) Data. Geophysics, 69, 1155-1165. https://doi.org/10.1190/1.1801933
- 6. 易柯, 张志勇, 李曼, 等. 基于FCM聚类算法的二维RMT电阻率与介电常数联合反演[J]. 地球物理学报, 2022, 65(6): 2340-2350.
- 7. 原源, 汤井田, 任政勇, 等. 基于非结构化网格的任意复杂2DRMT有限元模拟[J]. 地球物理学报, 2015, 58(12): 4686-4695.
- 8. Pek, J. and Verner, T. (1997) Finite-Difference Modelling of Magnetotelluric Fields in Two-Dimensional Anisotropic Media. Geophysical Journal International, 128, 505-521. https://doi.org/10.1111/j.1365-246X.1997.tb05314.x
- 9. De Groot-Hedlin, C. (2006) Finite-Difference Modelling of Magnetotelluric Fields: Error Estimates for Uniform and Nonuniform Grids. Geophysics, 71, 97-106. https://doi.org/10.1190/1.2195991
- 10. 薛帅, 白登海, 唐静, 等. 耦合PML边界条件的三维大地电磁二次场有限差分法[J]. 地球物理学报, 2017, 60(1): 337-348.
- 11. 童孝忠, 吴思洋, 谢维. 基于有限差分法的大地电磁二维倾子响应计算[J]. 工程地球物理学报, 2018, 15(4): 485-491.
- 12. 童孝忠, 吴思洋, 谢维. 利用非均匀网格有限差分法模拟二维大地电磁响应[J]. 工程地球物理学报, 2018, 15(3): 338-346.
- 13. Kalscheuer, T., Pedersen, L.B. and Siripunvaraporn, W. (2008) Radiomagnetotelluric Two-Dimensional Forward and Inverse Modelling Accounting for Displacement Currents. Geophysical Journal International, 175, 486-514. https://doi.org/10.1111/j.1365-246X.2008.03902.x
- 14. 周武, 罗威, 蓝星, 简兴祥. 大地电磁交错采样有限差分二维正反演研究[J]. 物探与化探, 2021, 45(2): 458-465.
- 15. 陈斌. 大地电磁测深TM模式二维有限差分正演研究[J]. 能源与环境, 2016(4): 17+21.
- 16. 徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994.