Optoelectronics
Vol.05 No.02(2015), Article ID:15504,6
pages
10.12677/OE.2015.52005
Numerical Calculation for Mueller Matrix of a Single Particle Based on Jones Vectors
Chaowei Zhou, Qinghua Wang*, Zhenhua Li
School of Science, Nanjing University of Science and Technology, Nanjing Jiangsu
*通讯作者。
Email: *qhwang@mail.njust.edu.cn
Received: Jun. 6th, 2015; accepted: Jun. 22nd, 2015; published: Jun. 25th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The formulae of a single particle’s scattering based on Jones vectors are derived. Then, the scattering Jones vectors of the single particle for the typical polarization states can be calculated. Further, the Stokes parameters can be obtained according to the scattering Jones vectors. The proper linear combination of the typical scattering Stokes parameters will provide the elements of Mueller matrix. The simulations for the single particle show that the subgraphs of the 2D Mueller matrix are symmetrical about the diagonal. The values for m41, m42, m43, m14, m24, m34 are all zeros. Only five subgraphs for the nonzero elements are independent and the others can be gained by rotation.
Keywords:Jones Vector, Stokes Parameters, Mueller Matrix, Scattering

基于Jones矢量的单粒子散射Mueller矩阵的数值计算
周超伟,王清华*,李振华
南京理工大学理学院,江苏 南京
Email: *qhwang@mail.njust.edu.cn
收稿日期:2015年6月6日;录用日期:2015年6月22日;发布日期:2015年6月25日

摘 要
本文推导了基于Jones矢量的单粒子散射的数学表达式;根据Jones矢量与Stokes参量的内在联系,给出了由典型偏振态的Jones矢量出发,计算Mueller矩阵的具体步骤。通过数值模拟得出单粒子对称系统中:二维Mueller矩阵4行4列共16个子图关于对角线对称;m41,m42,m43,m14,m24,m34数值为零;二维Mueller矩阵中非零元素子图中仅5幅独立,其余可通过旋转变换得到。
关键词 :Jones矢量,Stokes参量,Mueller矩阵,散射

1. 引言
当用Stokes参量来表示入射光的偏振状态时,各种光学转换器件的作用可以看作使入射光的Stokes参量发生改变,其变换矩阵用的Mueller矩阵来表示。Mueller矩阵的16个元素完整的反映了光学器件或被测介质的结构和功能信息,因此Mueller矩阵被称为被测介质的光学指纹。目前,研究生物组织等浑浊介质的偏振特性的普遍做法是通过其Mueller矩阵来分析介质对偏振光源的响应[1] 。获取Mueller矩阵的手段主要有实验测试和Monte Carlo方法。Mueller矩阵测试上,研究者主要在测量的简易性和精度上不断努力,例如:Hielscher等人 [2] 通过转动起偏器、1/4波片和检偏器的方向,测量光强49次,并通过计算得到Mueller矩阵;Espinosa-Luna [3] 在Hielscher的基础上改进测试装置,测量光强36次,计算出Mueller矩阵值;在Monte Carlo方法上,研究者在模拟的通用性上不断扩展,例如:Ramella-Roman等发表了Mueller矩阵值模拟的三种常用方法[4] [5] ;Wang等开发了时域Monte Carlo算法 [6] 。实验测试Mueller矩阵的误差不可避免,Monte Carlo方法也必须在模拟光子数目和模拟时间上进行折中 [7] 。本文基于入射光的Jones矢量,直接计算经过球形粒子散射后Stokes参量,再通过不同Stokes参量线性组合得到Mueller矩阵的相关列,为分析浑浊介质二维Mueller矩阵的模式提供了清晰的物理图景。
2. 偏振态的描述与转换矩阵
2.1. 基于Jones矢量的粒子散射模型
1941年Jones用在X,Y轴上互为正交的两个振动分量的合成来表示偏振光电矢量 [8] :
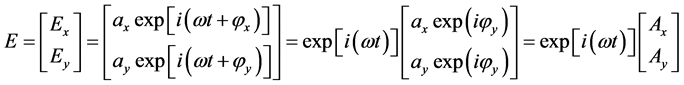 (1)
(1)
式中 ,
,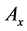 ,
,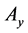 为复振幅。
为复振幅。
波的绝对位相不常用,重要的是相对位相差。省略(1)式中的光频项,采用位相差 ,并对各分量的振幅归一化,可得:
,并对各分量的振幅归一化,可得:
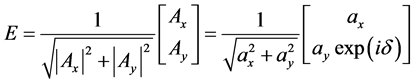 (2)
(2)
依照(2)式,水平直线偏振光,垂直直线偏振光,45˚直线偏振光,右旋偏振光的归一化Jones矢量分别为:
 ,
,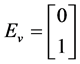 ,
,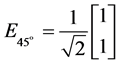 ,
,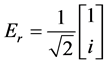
图1为光束遇到粒子散射的示意图。入射光可以正交分解成2个偏振分量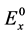 (水平)和
(水平)和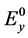 (垂直)。遇到粒子,入射光发生散射。散射后,光束传播方向变化角度
(垂直)。遇到粒子,入射光发生散射。散射后,光束传播方向变化角度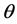 。粒子激发的散射电场为
。粒子激发的散射电场为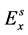 和
和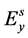 ,
,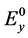 和
和 互相平行,
互相平行,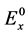 和
和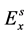 呈
呈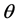 角。则经过粒子散射后的Jones矢量为:
角。则经过粒子散射后的Jones矢量为:
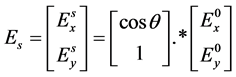 (3)
(3)
式中.*表示列向量的对应元素相乘。
事实上,全面描述粒子的散射除了散射角 外,还需要方位角
外,还需要方位角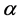 。方位角
。方位角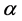 的取值范围为
的取值范围为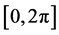 相同的散射角的散射光构成一锥形光束。为了说明方便,把光入射方向和散射方向确定的平面成为散射面。通常,总是让散射电场分量
相同的散射角的散射光构成一锥形光束。为了说明方便,把光入射方向和散射方向确定的平面成为散射面。通常,总是让散射电场分量 垂直于散射面,
垂直于散射面,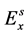 在散射面内。图1绘制入射光时,选取入射光的电场分量
在散射面内。图1绘制入射光时,选取入射光的电场分量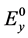 也垂直于散射面,这是为了得出比较简化的(3)式的一种特殊的选取方式。若(3)式中入射光对应坐标系
也垂直于散射面,这是为了得出比较简化的(3)式的一种特殊的选取方式。若(3)式中入射光对应坐标系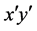 ,而更一般的入射光对应图2的坐标系xy。因此需要首先通过旋转矩阵把xy坐标系下的Jones矢量转换成
,而更一般的入射光对应图2的坐标系xy。因此需要首先通过旋转矩阵把xy坐标系下的Jones矢量转换成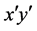 坐标系下的Jones矢量 [9] ,再运用(3)式计算散射后的Jones矢量,最后通过反向旋转矩阵把
坐标系下的Jones矢量 [9] ,再运用(3)式计算散射后的Jones矢量,最后通过反向旋转矩阵把 坐标系下的Jones矢量变回xy坐标系下的Jones矢量,整个转换过程如(4)式:
坐标系下的Jones矢量变回xy坐标系下的Jones矢量,整个转换过程如(4)式:
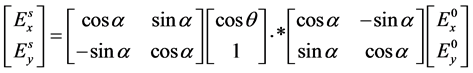 (4)
(4)
如图2所示,设散射粒子到平面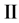 距离为h,探测器上的点A的坐标为
距离为h,探测器上的点A的坐标为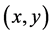 ,(4)式中的散射角
,(4)式中的散射角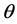 为:
为:
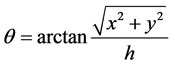 (5)
(5)
(4)式中的旋转角(方位角) 为:
为:
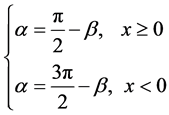 (6)
(6)
(6)式中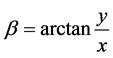 ,
, 。
。
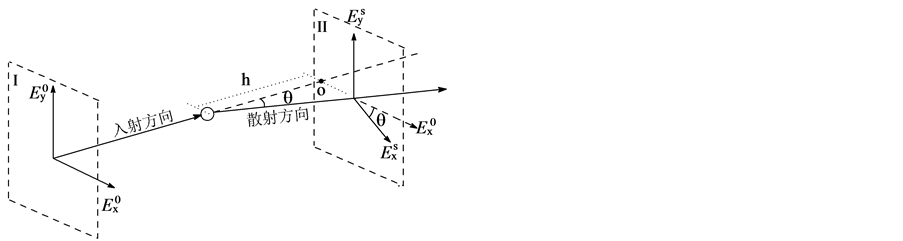
Figure 1. Schematic of particle scattering
图1. 粒子散射示意图

Figure 2. Schematic of rotating coordinate system
图2. 坐标系旋转示意图
2.2. Stokes参量与Mueller矩阵
早在1852年Stokes就使用一组都有由光强量纲的参量组成是Stokes参量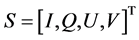 表征光的偏振态 [10] :
表征光的偏振态 [10] :
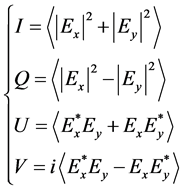 (7)
(7)
依照(7)式,水平直线偏振光,垂直直线偏振光,45˚直线偏振光,右旋偏振光的归一化Stokes参量分别为:
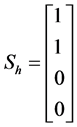 ,
, ,
, ,
,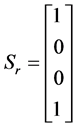
用Stokes参量表示入射光的偏振态,16个元素的Mueller矩阵M可表征被测系统对光的偏振态的改变:
 (8)
(8)
(8)式中S和S'分别为入射光和出射光的Stokes参量,M为系统的Mueller矩阵。Mueller矩阵含有16个元素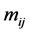 ,也可看成有4个列向量
,也可看成有4个列向量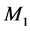 ,
, ,
, ,
,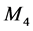 组成,如(9)式:
组成,如(9)式:
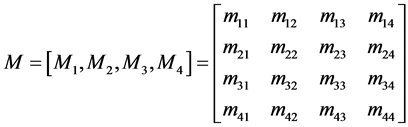 (9)
(9)
若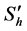 ,
,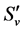 ,
,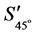 ,
,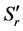 分别表示水平直线偏振光,垂直直线偏振光,45˚直线偏振光,右旋偏振光经过系统作用后的Stokes参量,则有:
分别表示水平直线偏振光,垂直直线偏振光,45˚直线偏振光,右旋偏振光经过系统作用后的Stokes参量,则有:
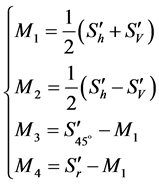 (10)
(10)
基于Jones矢量的Mueller矩阵计算的具体步骤为:1) 将典型偏振状态的Jones矢量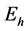 ,
,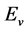 ,
,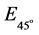 ,
,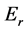 代入(4)式,得到散射后的Jones矢量
代入(4)式,得到散射后的Jones矢量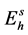 ,
, ,
,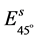 ,
,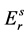 ;2) 根据(7)式得到散射后的Stokes参量
;2) 根据(7)式得到散射后的Stokes参量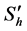 ,
, ,
,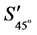 ,
,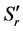 ;3) 根据(10)式计算出组成Mueller矩阵的4个列向量,从而得到Mueller矩阵的16个元素值。
;3) 根据(10)式计算出组成Mueller矩阵的4个列向量,从而得到Mueller矩阵的16个元素值。
3. 二维Mueller矩阵的数值模拟
随机介质界面的每点对应于一个Mueller矩阵等效为Mueller矩阵的每个元素在界面上呈现二维分布。图3给出了基于Jones矢量的单粒子二维Mueller矩阵的数值模拟图。模拟时,设定散射粒子到探测平面的距离为h为1 cm。图3中每幅子图代表Mueller矩阵16个元素在20 cm ´ 20 cm区域上的分布。从图3看出:对于探测器正下方的单粒子对称系统,二维Mueller矩阵关于对角线对称,即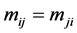 ;二维Mueller矩阵的第四行或者第四列的元素(除了
;二维Mueller矩阵的第四行或者第四列的元素(除了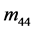 外)数值为零;非零元素仅仅有5幅(
外)数值为零;非零元素仅仅有5幅(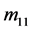 ,
,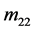 ,
, ,
,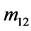 ,
, )是独立的,其余5幅通过对称、旋转变换可得到。这与文献报道的实验和理论分析分析吻合[11] 。需要指出的是,文献中的二维Mueller矩阵的
)是独立的,其余5幅通过对称、旋转变换可得到。这与文献报道的实验和理论分析分析吻合[11] 。需要指出的是,文献中的二维Mueller矩阵的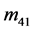 ,
,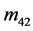 ,
,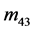 ,
,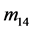 ,
,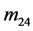 ,
,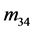 不全为0,似乎在这些元素上还有花样分布。但是在这些文献中
不全为0,似乎在这些元素上还有花样分布。但是在这些文献中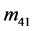 ,
,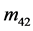 ,
,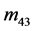 ,
,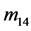 ,
, ,
,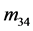 的花样分布与其它元素相比已经十分微弱。我们认为,导致文献中的与
的花样分布与其它元素相比已经十分微弱。我们认为,导致文献中的与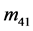 ,
,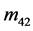 ,
, ,
,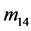 ,
,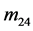 ,
,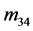 不严格为0的因素主要来源于两个方面:多个粒子的复散射和测量误差。
不严格为0的因素主要来源于两个方面:多个粒子的复散射和测量误差。
图4进一步绘制了散射粒子到探测平面的距离为h为5 cm的二维Mueller矩阵模拟图。图4中每幅子图仍然代表Mueller矩阵16个元素在10 cm ´ 10 cm区域上的分布。不难发现图3和图4的形状相似、对称关系一致。图3、图4中的环形以及辐射状子图数值的绝对值从中心点向四周随距离增大而衰减。图4的各子图花样可看作图3的各个子图的径向膨胀。图5绘出m11元素数值随径向距离的变化曲线。从图5看出,随着散射粒子距离h的增大,m11曲线变得平缓,当散射粒子距离h足够大时,考察区域的二维Mueller矩阵的花样将趋于消失,因为此时可以忽略散射粒子对探测器的影响。
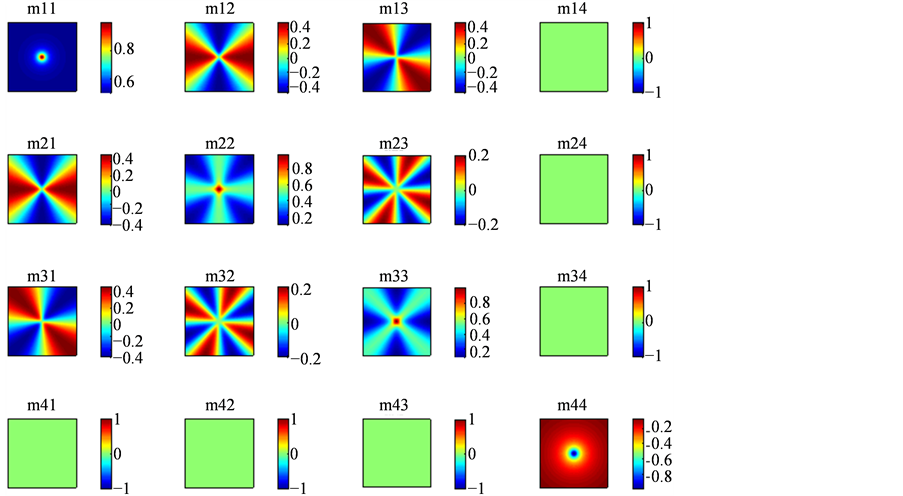
Figure 3. Simulation diagram of two-dimensional Mueller matrix (distance h from scattering particles to detecting plane is 1 cm)
图3. 二维Mueller矩阵模拟图(散射粒子到探测平面的距离h为1 cm)
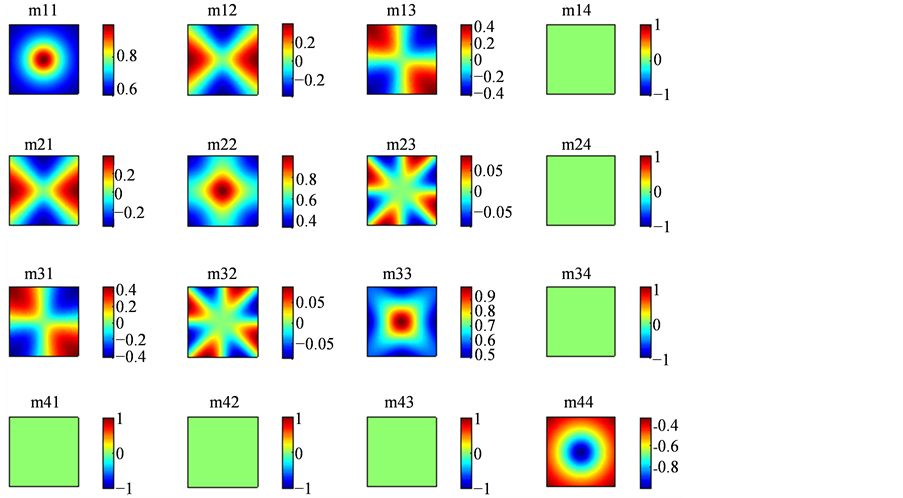
Figure 4. Simulation diagram of two-dimensional Mueller matrix (Distance h from scattering particles to detecting plane is 5 cm)
图4. 二维Mueller矩阵模拟图(散射粒子到探测平面的距离为h为5 cm)

Figure 5. Curve: value of m11 element with radial length
图5. m11元素数值随径向距离的变化曲线
4. 结论
Jones矢量和Stokes参量是两种表示光的偏振态的有效手段。本文推导了基于Jones矢量的单粒子散射模型,从而能够方便的获取水平直线偏振光、垂直直线偏振光、45˚直线偏振光、右旋偏振光经过单粒子散射后的Jones矢量。再根据Stokes参量定义,将单粒子散射后的Jones矢量换算成Stokes参量,最后通过不同Stokes参量的线性组合得到Mueller矩阵的各个列向量。本文提出的计算步骤,计算机上容易实现。通过数值模拟清晰的展示了单粒子对称系统中16个子图的特点,为分析随机介质的二维Mueller矩阵提供了一种简单有效的数值模拟手段。
文章引用
周超伟,王清华,李振华, (2015) 基于Jones矢量的单粒子散射Mueller矩阵的数值计算
Numerical Calculation for Mueller Matrix of a Single Particle Based on Jones Vectors. 光电子,02,26-32. doi: 10.12677/OE.2015.52005
参考文献 (References)
- 1. Ossikovski, R. and De Martino, A. (2015) Mueller matrix of a depolarizing homogeneous medium and its relation to the Mueller matrix logarithm. Journal of the Optical Society of America A, 32, 343-348.
- 2. Hielscher, A.H., Eick, A.A., Mourant, J.R., et al. (1997) Diffuse backscattering Mueller matrices of highly scattering media. Optics Express, 1, 441-453.
- 3. Espinosa-Luna, R. (2002) Scattering by rough surfaces in a conical configuration: Experimental Mueller matrix. Optics Letters, 27, 1510-1512.
- 4. Ramella-Roman, J.C., Prahl, S.A. and Jacques, S.L. (2005) Three Monte Carlo programs of polarized light transport into scattering media: Part I. Optics Express, 13, 4420-4438.
- 5. Ramella-Roman, J.C., Prahl, S.A. and Jacques, S.L. (2005) Three Monte Carlo programs of polarized light transport into scattering media: Part II. Optics Express, 13, 10392-10405.
- 6. Wang, X., Wang, L.V., Sun, C.W., et al. (2003) Polarized light propagation through scattering media: Time-resolved Monte Carlo simulations and experiments. Journal of Biomedical Optics, 8, 608-617.
- 7. 王清华, 李振华, 来建成, 贺安之 (2007) 随机介质背散射二维Mueller矩阵的数值模拟与分析. 光学与光电技术, 5, 1-4.
- 8. Jones, R.C. (1941) A new calculus for the treatment of optical systems. Journal of the Optical Society of America, 31, 500-503.
- 9. 阿查姆, R.M.A., 巴夏拉, N.M., (梁民基, 尹树百, 张福初, 等, 译) (1986) 椭圆偏振测量术和偏振光(中译版). 科学出版社, 北京, 51.
- 10. McMaster, W.H. (1954) Polarization and the Stokes parameters. American Journal of Physics, 22, 351-362.
- 11. Cameron, B.D. (1998) Measurement and calculation of the two-dimensional backscattering Mueller matrix of a turbid medium. Optics Letters, 23, 485-487.