E-Commerce Letters
Vol.07 No.03(2018), Article ID:26564,9
pages
10.12677/ECL.2018.73006
Campus Delivery Scheme Based on Dijkstra Algorithm
Jiakang Du1, Bohan Zhang2, Haodong Chen1, Qingjun Ren1, Hongchun Sun1
1School of Mathematics and Statistics, Linyi University, Linyi Shandong
2School of Information Science and Engineering, Jinan University, Jinan Shandong

Received: Aug. 2nd, 2018; accepted: Aug. 16th, 2018; published: Aug. 23rd, 2018

ABSTRACT
In recent years, with the development of science and technology and the improvement of people’s living standards, the emerging industry of take-out is developing rapidly, among which the fastest development is campus take-out. In this paper, by solving the problem of the shortest route of campus take-out, the problem of the delivery of campus take-out is equivalent to the shortest route problem. Dijkstra algorithm was used to obtain the best delivery scheme of campus take-out, and MATLAB program was compiled to determine the shortest route of campus take-out delivery. Finally, the validity and feasibility of the proposed algorithm are verified by an experimental example.
Keywords:Campus Takeout, The Shortest Circuit Problem, Dijkstra Algorithm
基于Dijkstra算法的校园外卖配送方案
杜家康1,张博瀚2,陈昊东1,任庆军1,孙洪春1
1临沂大学数学与统计学院,山东 临沂
2济南大学信息科学与工程学院,山东 济南

收稿日期:2018年8月2日;录用日期:2018年8月16日;发布日期:2018年8月23日

摘 要
近几年,随着科技的发展以及人们的生活水平提高,外卖这个新兴行业正在蓬勃发展,其中发展最快的莫过于是校园外卖。本文通过对校园外卖最短路线问题的优化求解,将校园内的外卖配送问题等效转化为最短路线问题,并运用Dijkstra算法求得校园外卖的最佳配送方案,编制了MATLAB程序,确定了校园外卖派送的最短路线。最后,通过实验算例验证了本文算法的有效性和可行性。
关键词 :校园外卖,最短路问题,Dijkstra算法

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近两年,随着电子商务的兴起以及送货上门服务的发展 [1] ,电子商务已经渗透到了我们生活的方方面面,校园外卖的迅速崛起就是最好的证明。由于恶劣天气、课业繁重、睡眠不足等等原因,越来越多的同学不想起身去餐厅吃饭,他们通常会选择订外卖的方式来节约时间。对饥饿的同学来说,最希望的就是外卖能够准时到达,但是由于商家配送外卖的数量多、宿舍楼分布错乱等问题,外卖常常不能够按时送达。所以,合理规划外卖路线是十分重要的,这样不仅可以为商家留住客户,更可以为商家送出更多的外卖,节省了运输成本,使商家获得更多的利润。我们通过对最短路线的研究,将外卖配送路线问题转化为最短路线问题进行研究。目前,国内外的专家学者对最短路线的问题也进行了较为深入的研究。比如,王树西等 [2] 分析了多邻接点问题与多条最短路径问题的成因对Dijkstra算法进行了改进;周康等 [3] 给出了固定端点的最短路问题闭环DNA算法;赵礼峰等 [4] 通过迭代矩阵和下标标注法对Floyd算法进行了改进,改进后的算法能快速地计算出网络中任意两节点之间的最短路长值;冯树民等 [5] 为了简化多目标最短路算法的问题,利用理想点法的优点,探索出一种多目标最短路问题的简便算法;丁秋雷,胡祥培等 [6] 针对干扰事件导致物流配送难以顺利实施这一难题,提出基于前景理论的扰动度量方法进行求解。本文根据Dijkstra算法的思想并在此基础上做出了改进,Dijkstra算法是保证源点到各个顶点之间的路程最短的求解最短路线的方法,而改进后的算法是在保证经过所有顶点的前提下,使得总的路线最短,这样就对外卖配送路线问题给出了优化设计方案,给出了算法步骤,并编制出了MATLAB程序。
2. 模型建立
在校园外卖配送过程中,按时到达是一件非常重要的事。而按时到达,取决于骑手配送外卖的速度。当外卖骑手最大速度一定的情况下,路线越短,配送的速度就越快。
由于校园外卖有如下几个特点:
1) 区域密集性。学生宿舍一般是聚集在某个区域内,宿舍楼在区域内密集分布。
2) 时间确定性。订餐时间一般在从午九点到下午一点、下午五点到七点。
3) 路线复杂性。各宿舍楼之间的连通的路线繁复。。
这就意味着,外卖骑手需要在一个固定的时间、一块密集的宿舍楼区域、一段曲折蜿蜒、岔路丛生的路上配送尽可能多的外卖。倘若走错了一个路口,那很可能需要绕一圈路才能到达目的地。
由此带来的不仅是顾客的不满、骑手的金钱损失、甚至于商家的信誉损失。所以给出一条从商家到客户的最短路线是十分重要的。
现给出一个以起点(1)为起始点的有向图图G,如图1所示。
其中,在有向图图G中,存在n个连接点与m条连接各点的路径,在图一的所有路径中,不同路径有不同的权值,寻找以起点(1)为起始点,连接其余 个点的最短路径。
本文根据两种不同情况下提出求解最短路径的方法:
1) 单条路径最短路线求解,在图1中寻找一条路径经过其中所有的连接点,使得求得最短路径的权值和最小。
2) 多条路径最短路线求解,在图1中寻找多条路径经过其中所有的连接点,使得求得最短路径的权值和最小。
2.1. 单条路径最短路线求解(附录1)
已知起始点的位置是固定的,由起始点开始由一条最短路径连接剩下的连接点.在已知相互各点之间的权值的情况下,找出与起始点权值最小的连接点 ,然后再以 点为起始点找出与它相连的权值最小的连接点,以上述规则进行迭代,每次都选取最小的权值,最终所形成的路径的权值也会是最小的,即最短路线.下面利用矩阵的形式表示上述方案:
Step 1:将各点之间的权值在矩阵中表示出来, 为 点与 点之间的权值,由此建立一个 的矩阵 。
其中,矩阵 中当 时表示的为自身之间的距离,为避免对结果造成影响,故设为无穷大数,即 。
Step 2:比较矩阵 的第一列,得出第一列的最小值 ,即与起始点相连的点中, 点与起始点之间的权值最小。
Step 3:再以 点为起点,找与 点之间权值最小的点。在矩阵 的第 行,比较 行中各个元素的大小,可得第 行中最小的元素为 ,其含义为 点与 点之间的权值最小。输出点 ,将元素 所在的列上所有的元素都变为无穷大值,得到矩阵 。
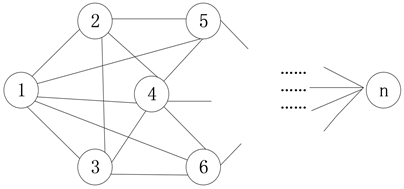
Figure 1. Directed graph with starting point (1) as the starting point
图1. 以起点(1)为起始点的有向图图G
Step 4:以点m为起点,依照第三步的步骤进行迭代,直至路线经历所有点。根据依次输出的值的列序号就能得出单条路径情况下的最短路线。
本方案是基于迭代思想并且运用矩阵给出的算最短路径的方法,该方法简单易懂,过程相对简单,不过对于计算机要求较高,运算起来较为麻烦,对前期数据要求较为具体,但是也从迭代的方面提出了最短路径的算法。
2.2. 多条路径最短路线求解(附录2)
对于该问题的求解,我们给出两种成熟且稳定的算法:
1) 枚举法
枚举法是指找出连接上述 个点的所有路径,分别求出每条路径的权值,最后比较各条路径的权值
大小,从而找出最短路径。但是连接各点路径最多将会有 条,当 很大时,利用枚举法将会耗费大量的时间和精力。
2) Dijkstra法
Dijkstra法是一种基于矩阵和集合的思想来求最短路径的方法,具体步骤如下:
Step 1:创立两个集合 ,其中 集合存放源点,指路径出发的点, 集合存放待定点,指路径到达的终点。
Step 2:比较各源点与待定点之间的权值,将权值最小的两点连线,将此待定点加入源点集合 。
Step 3:重复第二步,直到待定点全部加入源点集合 。待定点加入源点集合的顺序即路径行走的顺序。
接下来我们通过矩阵形式来表示上述过程:
首先,我们先提出两个假设:
①假设不存在孤立点,各连接点至少由一条路径与其他连接点相连;
②自身与自身相连表示权值为无穷,两点之间不相连表示权值为无穷。
根据假设,图1可用矩阵表示为
其中 , , 表示为 两点之间的权值。
①在矩阵 中找到源点所对应的行向量 。如以点1为源点,源点矩阵 。
②在源点矩阵 寻找权值最小的 ,其中 为源点, 为待定点。
③将 点对应的行向量加入源点矩阵 , ,在其中以无穷大替换步骤②找出的最
小值 。
对源点矩阵 循环实行②③步,直至源点矩阵 的维数与矩阵 相同。待定点加入源点矩阵的顺序即路径行走的顺序。
2.3. 算法比较
枚举法与迪杰斯特拉法相比,过程清晰,结果精确度高,原理简单明了,可一旦连接点的个数变多,运算过程就会变得冗杂、繁复、实际应用时问题很大。Dijkstra法的好处在于不需要数据运算,只需要进行简单的比较就能得出结果,并且能够剔除已知的结果,使得下一步过程进一步简化。由此可知,在面对实际应用时,Dijkstra法能够快速的找到最佳的多条路径最短路线方案。
3. 数值算例
某学校有五座宿舍楼,外卖商家与五座宿舍楼不在一处。已经给出五座宿舍楼之间的距离和五座宿舍楼与商家的距离,如表1所示。假设骑手的配送速度固定,现要求给出两种方案,一种是当只有一个外卖骑手配送外卖时的最短路线;另一种是由多位外卖骑手共同配送外卖时的最短路线。上述两种方案中,要求骑手经过所有宿舍楼且配送外卖的时间最短。
已知骑手的速度 一定,要求找出最佳方案,使得骑手配送外卖的时间 最短。再由简单的物理知识
路程(s) = 时间(t) × 速率(v)可知:“ ”,即配送路线距离越小,配送外卖所用的时间越短。由此,
将最短时间问题转化为最短路线问题。
假设外卖骑手的配送速度为 ,配送时间为 ,配送路线距离为 ,其中配送速度已知。由于
,故求出最短路线的距离 即可。
Step 1:作出路线图
Table 1. The distance between any two points
表1. 任意两地点之间的距离
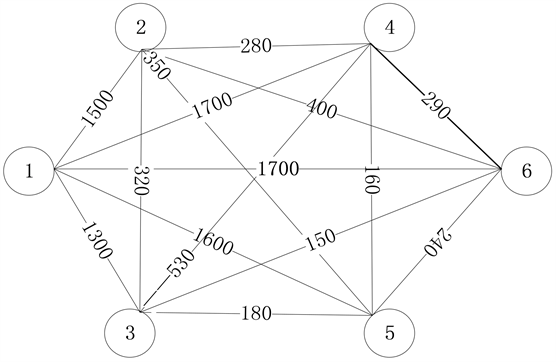
Figure 2. A road map from known data
图2. 由已知数据得出的路线图
Step 2:将表1使用矩阵的形式表述
为了使得运算过程简单方便,在此采取两个小技巧,规定自己本身相连的距离为无穷 ;若两座宿舍楼不直接相连,规定它们之间的距离为无穷,矩阵变为:
Step 3:最短路线求解
①单人配送外卖方案
通过单条最短路径求解中求解原理编译的MATLAB程序
可直接解得
, ,
其中,矩阵 储存每一步迭代过程取出的最小值;矩阵 储存每步迭代取出的连接点,并且连接点的顺序就是最短路径的顺序; 为最短路径的长度。
具体路线图如图3所示
②多人配送外卖方案
通过多条最短路径求解中Dijkstra法的求解原理编译的MATLAB程序
可直接解得
, ,
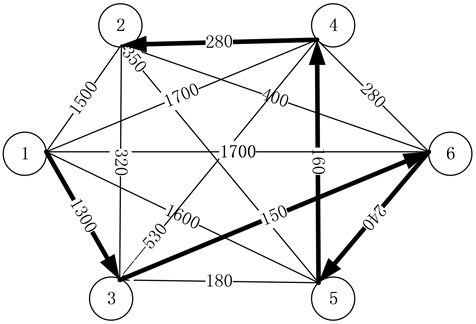
Figure 3. The shortest route to deliver take-out by one person
图3. 单人配送外卖的最短路线方案
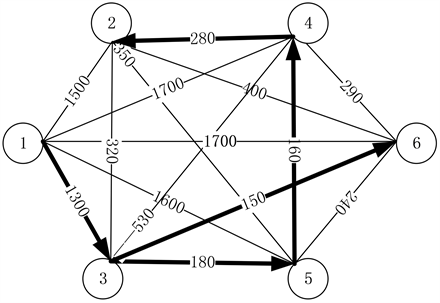
Figure 4. The shortest route to delivery take-out by many people
图4. 多人配送外卖的最短路线方案
其中,矩阵 储存每一步迭代过程取出的最小值;矩阵 储存每步迭代取出的连接点,并且连接点的顺序就是最短路径的顺序; 为最短路径的长度。
具体路线图如图4所示。
文章引用
杜家康,张博瀚,陈昊东,任庆军,孙洪春. 基于Dijkstra算法的校园外卖配送方案
Campus Delivery Scheme Based on Dijkstra Algorithm[J]. 电子商务评论, 2018, 07(03): 38-46. https://doi.org/10.12677/ECL.2018.73006
参考文献
- 1. 邓佩, 苏翔. 时间约束下的运输网络最短路径研究[J]. 机电产品开发与创新, 2006, 19(1): 18-20.
- 2. 王树西, 李安渝. Dijkstra算法中的多邻接点与多条最短路径问题[J]. 计算机科学, 2014, 41(6): 217-224.
- 3. 周康, 同小军, 刘文斌, 等. 最短路问题的闭环DNA算法[J]. 系统工程与电子技术, 2008, 30(3): 556-560.
- 4. 赵礼峰, 梁娟. 最短路问题的Floyd改进算法[J]. 计算机技术与发展, 2014(8): 31-34.
- 5. 冯树民, 吴海月, 王弟鑫. 基于理想点法的多目标最短路求解算法研究[J]. 公路交通科技, 2016, 33(3): 97-101.
- 6. 丁秋雷, 胡祥培, 姜洋. 基于前景理论的物流配送干扰管理模型研究[J]. 管理科学学报, 2014, 17(11): 1-9.
附录
附录1:单人配送外卖方案MATLAB程序
function [U,V,d]=lcxz(A)
b=inf;
[m,n]=size(A);
B=A;
U=zeros(1,n);
V=ones(1,n);
R=b*ones(1,n);
L=b*ones(m,1);
a=A(1,:);
[u,v]=min(a);%计算与初始点相连的第一个点
B(1,:)=R;
B(:,1)=L;
t=1;
U(1,2)=u;
V(1,2)=v;
for i=2:n-1%循环计算经过路径
s=v;
f=B(v,:);
t=i+t;
[u,v]=min(f);
U(1,i+1)=u;
V(1,i+1)=v;
B(s,:)=R;
B(:,s)=L;
i=i+1;
end
U;%存储最短两点之间的权值
V;%存储最短路线经过的节点
d=sum(U);%最短路线的总距离
附录2:多人配送外卖方案MATLAB程序
function [U,V,d]=ndjtsl(A)
b=inf;
[m,n]=size(A);
C=inf*ones(n);
B=A;
U=zeros(1,n);
V=ones(1,n);
rep=b;
a=B(1,:);
[u,v]=min(a);%计算与初始点相连的第一个点
B(1,v)=rep;
B(v,1)=rep;
U(1,2)=u;
V(1,2)=v;
f=B(1,:);
for i=3:n %循环计算经过路径
r=v;
F=[f;B(v,:)];
[u,v]=min(F,[],2);
rv=v;
[u,v]=min(u);
U(1,i)=u;
x=v;
s=V(x);
y=rv(v);
v=y;
V(1,i)=y;
B(r,y)=rep;
B(y,r)=rep;
B(s,y)=rep;
B(y,s)=rep;
f=[f;B(r,:)];
f(x,y)=rep;
i=i+1;
end
U;%存储最短两点之间的权值
V;%存储最短路线经过的节点
d=sum(U);%最短路线的总距离
