Modeling and Simulation
Vol.07 No.03(2018), Article ID:26268,7
pages
10.12677/MOS.2018.73016
Research on Pipeline Leakage Detection Model Based on Finite Volume Method Godunov Scheme
Yue Zhao1, Ling Zhou1*, Lianwei Gao2, Yanxiu Dai2, Deyou Liu1, Yun Cao1, Tianwen Pan1
1College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing Jiangsu
2State Grid Xinyuan Company LTD Baishan Pumped Storage Power Station, Jilin Jilin

Received: Jul. 9th, 2018; accepted: Jul. 26th, 2018; published: Aug. 6th, 2018

ABSTRACT
Finite volume method with first order and second order Godunov schemes is presented to simulate and analyze the pipeline leakage problem. The water hammer equation is discrete by Riemann, and the MUSCL-Hancock method is used to reconstruct the two-order precision Godunov format. In order to avoid the false oscillation, the MINMOD slope limiter is introduced, and the leakage detection model is established by combining the leakage boundary conditions. The two-order Godunov scheme is consistent with the result of the characteristic line method, thus verifying the correctness of the model. The calculation analysis shows that the pressure curve of the leakage pipe is attenuated and deformed, while the pressure curve of the whole pipe does not attenuate and deform; the leakage flux affects the attenuation amplitude of the curve, and the greater the leakage flow, the greater the attenuation amplitude of the curve; the number of leakage points determines the number of inflection points at the peak curve, and the location of the leakage point determines the curve. According to the pressure curve of the leakage pipe, the leakage, the number of leakage points and the location of the leakage can be judged by the time of the inflection point of the shape and the first wave peak. This has important theoretical significance and practical guidance value for pipeline leakage monitoring.
Keywords:Finite Volume Method, Godunov Scheme, Leakage Detection
基于有限体积法Godunov格式的管道泄漏检测模型研究
赵越1,周领1*,高连伟2,戴彦秀2,刘德有1,曹云1,潘天文1
1河海大学水利水电学院,江苏 南京
2国网新源控股有限公司白山抽水蓄能电站,吉林 吉林

收稿日期:2018年7月9日;录用日期:2018年7月26日;发布日期:2018年8月6日

摘 要
针对管道泄漏问题,采用有限体积法Godunov格式对其进行数值建模和计算分析。通过Riemann对水锤方程进行离散,采用MUSCL-Hancock方法进行重构得到二阶精度的Godunov格式,为了避免虚假振荡引入MINMOD斜率限制器,结合泄漏边界条件建立泄漏检测模型。二阶Godunov格式与特征线法的计算结果一致,从而验证了所建模型的正确性。计算分析表明,泄漏管道的压力曲线发生衰减和变形,完整管道的压力曲线不发生衰减和变形;泄漏流量影响曲线的衰减幅度,泄漏流量越大曲线衰减幅度越大;泄漏点的数量决定曲线峰值处拐点数量;泄漏点位置决定曲线的形状和第一个波峰发生拐点的时间,从而可以根据泄漏管道的压力曲线,判断管道是否发生泄漏、泄漏点的数量、泄漏发生位置。这对管道泄漏监测具有重要理论意义和实际指导价值。
关键词 :有限体积法,Godunov格式,泄漏检测

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在供水管道中经常发生泄漏事故,这不仅对水资源造成浪费同时也对经济造成严重的损失。因此,为了减少泄漏管道对人类生产生活以及经济造成的损失,及时并准确的检测管道中泄漏点的位置至关重要。近年来,基于瞬变流进行泄漏检测的方法也被国内外学者广泛应用。Chaudhry等 [1] 基于瞬变流反问题分析提出了频率响应的管道泄漏检测技术,同时用特征线法计算并与实验结果比较。Tahvaei等 [2] 通过瞬间关闭阀门引起的压力波的反射,用子波滤波数据,然后用倒谱来提取反射点从而检测到泄漏位置。Krohn等 [3] 提出了一种利用频率响应检测管道泄漏的新技术并能够预测泄漏的位置和放电。Hamid等 [4] 介绍了一种基于逆瞬态分析的管道泄漏检测新方法,并将反问题应用到泄漏检测中。郭新蕾等 [5] [6] [7] 基于瞬变流的全频域法、遗传算法和瞬变压力波法对泄漏管道进行泄漏检测。伍悦滨等 [8] 采用反问题瞬变分析对给水管道的漏失进行数值模拟。孙良等 [9] 基于特征线法以及管道泄漏的瞬变过程,来获取泄漏的信号并对其在管道中的传播进行研究。李若珊 [10] 建立了长输燃气管道的泄漏瞬变模型,并进行大量仿真计算。王通等 [11] 通过瞬变压力值的谐波分析,来对输油管道的泄漏进行检测,并且通过频域响应模型描述了瞬变流的解决方法。可以看出,国内外学者大多采用基于瞬变反问题分析的模型和基于瞬变流的频域响应模型进行泄漏检测,其中基于瞬变反问题分析的模型对数学模型的精度要求非常高,需要前几周期模拟的数值结果较为准确,并且模拟过程较为复杂。此外,大多数学者都是基于特征线法对泄漏管道进行模拟。Ming等 [12] 指出在达到相同精度的情况下,二阶Godunov格式比MOC方法效率更高。本文为提高计算效率采用二阶Godunov格式对管道泄漏模型进行数学建模,并通过算例分析验证二阶Godunov格式对于模拟泄漏检测模型的准确性以及泄漏流量、泄漏点数量和泄漏位置对曲线的影响,从而检测出泄漏点的具体位置并有效阻止泄漏损失进一步扩大。
2. 数学模型
2.1. 基本控制方程
将描述管道水流状态的运动方程和连续性方程 [13] 写成以下矩阵的形式:
(1)
其中, ; ; 。
式中,x为沿管轴线方向的距离;t为时间;H为测压管水头;V为管道内水流流速;a为波速;g为重力加速度;f为恒定摩阻系数;D为管道直径。
(2)
式中,fi −1/2为i − 1/2界面数值通量;fi + 1/2为i + 1/2界面数值通量。
(3)
式中: 为n时刻u在 界面左侧的平均值, 为n时刻u在 界面右侧的平均值, , 。
2.2. 二阶Godunov格式
用MUSCL-Hancock [14] 方法进行线性重构得到二阶Godunov格式的步骤如下:
第一步:数据重构
(4)
(5)
其中:上角标L表示 且 ;上角标R表示 且 ; , 。
第二步:推进时间计算
(6)
(7)
第三步:Riemann问题的近似求解
(8)
将式(8)代入式(3)中即可得到二阶Godunov格式在 时刻所有控制体界面 的通量值。
2.3. 泄漏边界条件
如图1所示泄漏发生在管道第i个单元处,然后根据流量连续方程可得:
 (9)
(9)
其中,Vleak泄漏处流速; 、 分别为泄漏单元左侧和右侧界面的流速。
不考虑泄漏处的局部水头损失,即假设泄漏处压力水头与泄漏单元左、右界面的压力水头相同:
(10)
其中,Hleak为泄漏处的压强水头; , 分别为泄漏单元左右界面的测压管水头。
对于泄漏单元左侧界面,根据正向特征线可得:
(11)
对于泄漏单元右侧界面,根据负向特征线可得:
(12)
根据孔口出流公式,可得泄漏处流量:
(13)
式中,CdAg为泄漏系数;Hout为管道外部压力;A1为管道的横截面积。
联立方程(9)~(13)即可得到泄漏单元的水头及流量。
3. 算例分析
本文采用上游水库-管道-下游阀门的简化模型,管道长为1000 m,波速为a为1000 m/s,上游水库Hr为50 m,管道直径为0.2 m,初始流量为0.02 m3/s,重力加速度g为9.806 m/s2,计算时间为4.0 s,下游阀门瞬间关闭,本文在数值模拟过程中假定:1) 即使低于水体汽化压力,也不发生液柱分离现象;2) 管
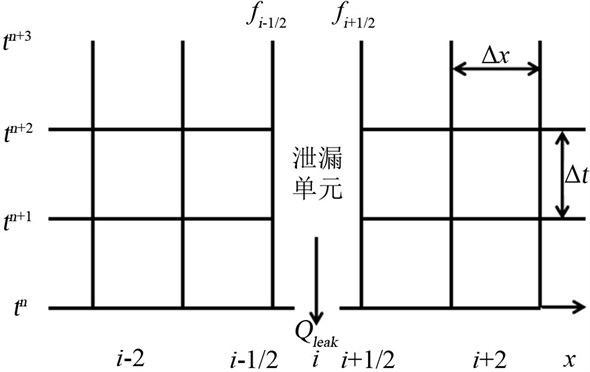
Figure 1. The schematic diagram of leakage unit
图1. 泄漏单元示意图
道为无摩阻管道,则压力计算结果衰减均为数值计算耗散(误差)引起。
3.1. 完整管道与泄漏管道对比
方案1:基于MOC方法对完整管道和泄漏管道进行数值模拟并计算阀前的压力水头;基于二阶Godunov格式对泄漏管道进行数值模拟并计算阀前的压力水头。其中,泄漏位置位于管道中心,泄漏流量为0.001 m3/s。如图2(a)所示,对于泄漏管道,Godunov的二阶格式与MOC方法的曲线完全重合,说明对于无摩阻的泄漏管道,Godunov的二阶格式与MOC方法计算结果一致,验证了在模拟泄漏管道方面Godunov的二阶格式具有准确性。
如图2(a)所示,观察曲线变化情况,可知当管道不发生泄漏时,曲线没有衰减现象。当管道发生泄漏时,曲线出现大幅度的衰减并产生明显的变形。由于管道为无摩阻管道,所以曲线的衰减完全由能量的耗散产生,即管道产生的泄漏流量是导致曲线衰减的根本原因。观察曲线的拐点,可知当水锤波传递到泄漏点时会发生反射,反射的降压波会使阀前的压力水头降低,由于水锤波不断反射,所以压力曲线会产生多个拐点。综上所述,管道存在泄漏点会导致曲线发生衰减和拐点,从而可根据压力曲线的衰减情况和是否发生变形来判断管道有无泄漏点。
3.2. 泄漏参数对曲线的影响
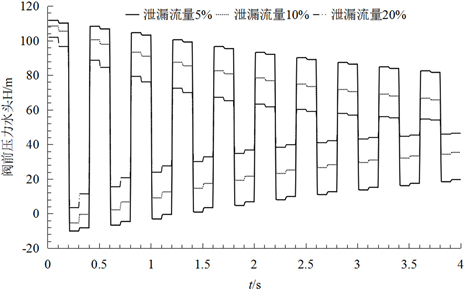
方案2:基于二阶Godunov格式计算泄漏位置为管道中心且泄漏流量分别为0.001 m3/s、0.002 m3/s和0.004 m3/s (分别为初始流量的5%、10%和20%)的阀前压力水头。如图2(b)所示,三种泄漏流量情况
 (a) 方案1
(a) 方案1
 (b) 方案2
(b) 方案2
 (c) 方案3
(c) 方案3
 (d) 方案4
(d) 方案4
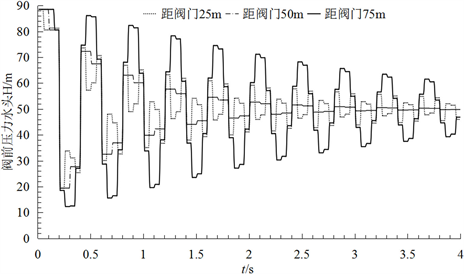
Figure 2. Pressure head traces at valve
图2. 阀前压力水头值
下的曲线均出现衰减,且泄漏流量越大衰减幅度越大,说明发生泄漏的位置相同时泄漏流量越大,能量消耗越快。同时,三种泄漏流量情况下发生变形的位置相同,说明管道泄漏点的位置相同,曲线发生变形的位置相同。由此说明,泄漏流量影响曲线衰减幅度,泄漏位置影响曲线发生变形的情况。
方案3:基于二阶Godunov格式计算泄漏流量为0.001 m3/s,泄漏点的数量分别为1个、2个和3个时阀前的压力水头。如图2(c)所示,曲线峰值处的拐点个数分别为1个、2个和3个,与泄漏点的个数完全相同,并且泄漏点越多曲线衰减越剧烈。由此说明,泄漏点的个数与曲线峰值处拐点个数相同。
方案4:基于二阶Godunov格式计算泄漏流量为0.004 m3/s且泄漏位置分别为距下游阀门25 m、50 m、和75 m (相应1/4、1/2和3/4)的阀前压力水头。如图2(d)所示,当发生泄漏的位置与阀门距离占管道总长比例大于的1/2时,曲线呈现“凸”形。当发生泄漏的位置与阀门距离占管道总长比例小于的1/2时,曲线呈现“凹”形,并且相同泄漏流量情况下,关于中点对称的泄漏点位置的曲线凹凸程度基本相同,而中点凹凸程度相比于其他泄漏点大幅度减小,说明泄漏位置不仅影响曲线的形状,同时影响曲线的凹凸程度。综上所述,可以根据曲线的形状判断发生泄漏的大概位置,(即管段前半部分、管段中心和管段后半部分)。
如图2(d)所示,泄漏发生位置不同时,波峰发生的拐点位置不相同,并且通过计算得到三种情况下第一个波峰产生拐点的时间分别为0.05 s、0.1 s、和0.15 s,而水锤波在管道中传递的半个周期所需时间为2 L/a = 0.2 s,由此可知,产生拐点的时间分别为水锤波在管道中传递半个周期所需时间的1/4、1/2和3/4,与发生泄漏的位置占管道总长的比例相同,此外,第二个波峰发生拐点的时间分别为0.45 s、0.5 s和0.55 s,分别减去水锤波传递一个周期所需的时间则仍为0.05 s、0.1 s、和0.15 s,与第一个波峰处相同,所以第二波峰处发生拐点的时间依然与泄漏位置有关。由于第一波峰发生拐点时间计算泄漏发生的位置更为简便,因此本文根据第一个波峰拐点发生的时间来得到泄漏发生的具体位置。
4. 结论
1) 二阶Godunov格式与MOC方法对于无摩阻的泄漏管道数值模拟结果完全一致,从而验证二阶Godunov格式模拟管道泄漏是准确可行的。
2) 管道是否发生泄漏对压力曲线的影响差别较大,管道发生泄漏会令曲线产生衰减,其中泄漏流量影响曲线的衰减幅度,即泄漏流量越大曲线衰减幅度越大。
3) 管道发生泄漏会令曲线产生变形,其中可从峰值处产生的拐点个数判断管道存在的泄漏点数量,然后从曲线向内呈现“凹”形或者向外呈现“凸”形来判断泄漏的大概位置,最后根据第一波峰发生拐点的时间确定管道发生泄漏的具体位置。
基金项目
国家电网公司科技项目资助(合同号:SGBXSJJS1700007);国家自然科学基金项目资助(编号:51679066)。
文章引用
赵越,周领,高连伟,戴彦秀,刘德有,曹云,潘天文. 基于有限体积法Godunov格式的管道泄漏检测模型研究
Research on Pipeline Leakage Detection Model Based on Finite Volume Method Godunov Scheme[J]. 建模与仿真, 2018, 07(03): 129-135. https://doi.org/10.12677/MOS.2018.73016
参考文献
- 1. Lee, P.J., VTkovsk, J.P., Simpson, A.R., et al. (2002) Leak Detection in Pipes by Frequency Response Method Using a Step Excita-tion. Journal of Hydraulic Research, 41, 221-223. https://doi.org/10.1080/00221680309499965
- 2. Taghvaei, M., Beck, S.B.M. and Boxall, J.B. (2010) Leak Detection in Pipes Using Induced Water Hammer Pulses and Cepstrum Analysis. International Journal of Comadem, 13, 19-25.
- 3. Krohn, N. and Busse, G. (2002) Leak Detection in Pipelines Using the Damping of Fluid Transients. Journal of Hydraulic Engineering, 128, 697-711. https://doi.org/10.1061/(ASCE)0733-9429(2002)128:7(697)
- 4. Hamid Shamloo, A. and Candidate, A.H. (2009) Leak Detection in Pipelines by Inverse Backward Transient Analysis. Journal of Hydraulic Research, 47, 311-318. https://doi.org/10.1080/00221686.2009.9522002
- 5. 郭新蕾, 杨开林. 管道泄漏检测的水力瞬变全频域数学模型[J]. 水利学报, 2008, 39(10): 1264-1271.
- 6. 郭新蕾, 杨开林. 管道系统泄漏检测的瞬变水击压力波法[J]. 应用基础与工程科学学报, 2011, 19(1): 20-28.
- 7. 郭新蕾, 杨开林, 郭永鑫. 管道泄漏检测全频域法试验验证及抗噪性研究[J]. 水利学报, 2011, 39(6): 713-720.
- 8. 伍悦滨, 刘天顺. 基于瞬变反问题分析的给水管网漏失数值模拟[J]. 哈尔滨工业大学学报, 2005, 37(11): 1483-1485.
- 9. 孙良, 王建林. 基于泄漏瞬变模型的管道泄漏检测与定位方法[J]. 应用基础与工程科学学报, 2012, 20(1): 159-168.
- 10. 李若珊. 基于瞬态模拟的长输燃气管道泄漏检测方法研究[D]: [硕士学位论文]. 哈尔滨: 哈尔滨工业大学, 2005.
- 11. 王通, 阎祥安, 李伟华. 基于谐波分析的输油管道泄漏检测机理研究[J]. 化工自动化及仪表, 2005, 32(1): 51-54.
- 12. Zhao, M. and Ghidaoui, M.S. (2004) Godunov-Type Solutions for Water Hammer Flows. Journal of Hydraulic Engi-neering-Asce, 130, 341-348. https://doi.org/10.1061/(ASCE)0733-9429(2004)130:4(341)
- 13. Wylie, E.B. and Suo, V.L.S. (1993) Fluid Transients. McGraw-Hill, New York, 1-40.
- 14. Toro, E.F. (2009) Riemann Solvers and Numberical Methods for Fluid Dynamics. Verlag Berlin Heidelberg, Berlin, 115-125. https://doi.org/10.1007/b79761_4