Modeling and Simulation
Vol.
09
No.
01
(
2020
), Article ID:
33495
,
10
pages
10.12677/MOS.2020.91003
Aerodynamic Characteristic Analysis of Box Girder Section in TSI Gusty Wind
Fei Huang, Lin Huang*, Junji Zhou
School of Civil Engineering, Architecture and Environment, Xihua University, Chengdu Sichuan

Received: Nov. 27th, 2019; accepted: Dec. 10th, 2019; published: Dec. 17th, 2019

ABSTRACT
The aerodynamic forces on box girder section and flow field are simulated by CFD (computational fluid dynamics) method in TSI (Technical Specifications for Interoperability) gusty wind at the angles of attack from −5˚ to +5˚. Reynolds-averaged Navier-Stokes (RANS) equations for 2D incompressible unsteady flow are integrated with RNG (Renormalized Group) k-ε turbulence model in this research. The time histories of the aerodynamic forces on the box girder section in TSI gusty wind slowly fluctuate around the reference values based on the quasi-steady assumption, but the oscillation amplitudes at high angles of attack are relatively large. The sudden change of drag coefficient, the change of lift coefficient lagging the wind speed of the TSI gust, and the favorable and adverse pressure gradients are observed and analyzed.
Keywords:TSI Gusty Wind, Box Girder Section, Aerodynamic Characteristic, Numerical Simulation

TSI阵风作用下箱梁断面的气动特性分析
黄菲,黄林*,周俊吉
西华大学土木建筑与环境学院,四川 成都

收稿日期:2019年11月27日;录用日期:2019年12月10日;发布日期:2019年12月17日

摘 要
采用二维非定常不可压缩雷诺平均N-S方程结合RNG k-ε湍流模型,模拟分析了TSI (Technical Specifications for Interoperability)阵风以−5˚~+5˚攻角作用下箱梁断面的气动力及流场特性。TSI阵风作用过程中,箱梁断面的气动力总体上围绕准定常假设的气动力做小幅波动,但较大风攻角时箱梁断面的气动力波动幅度较大。分析探讨了箱梁断面的阻力系数跳跃现象、升力系数变化滞后于TSI阵风风速变化、流场静压分布的顺压和逆压梯度特性等。
关键词 :TSI阵风,箱梁断面,气动特性,数值模拟

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
非定常风速的模拟通常有以下3种方法:1) 阵风系数法将非定常风速简化为定常风速,采用风速峰值计算风荷载。对于动力响应不敏感的刚性桥梁结构可采用该方法。如,公路桥梁抗风设计中采用静阵风系数计算±3˚风攻角内桥梁主梁的横向最大静阵风荷载 [1] [2]。2) 频域方法基于风谱表达非定常的风速,然后在时域进行动力响应分析。该方法能够充分考虑结构与动力响应间的相关性 [3]。3) 理想阵风法采用时间相关确定阵风时程,采用积分法计算系统的动力响应。该方法可以快速获得系统的最大响应,不需要进行复杂的分析计算。TSI (Technical Specifications for Interoperability)阵风模型 [4] 就是其中一种,可以有效近似风速最大值邻域的随机过程,常用于横向风作用下列车的脱轨分析 [5] [6]、带风屏障的高架桥上的高速列车的气动特性分析 [7]。在这些应用研究中,均基于准定常假设,直接应用静力三分力系数计算TSI阵风作用下列车的气动力。本文基于冻结湍流假设(frozen turbulence hypothesis) [8] [9],应用FLUENT软件,采用CFD (Computational Fluid Dynamics)方法研究TSI阵风作用过程中箱梁断面的气动力及流场特性。
2. 物理模型
2.1. 阵风模型
本文采用仅考虑确定性阵风部分TSI阵风模型 [4] [7]。阵风风速 定义:
(1)
式中,U为相应的均匀来流风速,取 ; 为考虑阵风效应的系数:
(2)
式中,A为静阵风风速振幅,根据文献 [4] [7] 取1.7。
2.2. 箱梁模型及计算域
参考文献 [10] 中的桥梁模型,箱梁断面如图1所示。风攻角采用 。CFD计算时取缩尺比1:40。为了防止箱梁断面附近的分离旋涡由外边界反射回流场、外边界附近的流场参数分布与外边界条件不相容,计算域(如图2)取20B × 30B的矩形区域(B为箱梁断面的计算宽度,B = 0.30 m),以确保计算结果收敛。其中,入口及上/下侧边界距离箱梁断面形心10B、出口边界距离箱梁断面形心20B。计算域边界定义:入口边界为速度入口(velocity-inlet)、上下边界为对称边界(symmetry)、出口边界为压力出口(pressure-outlet)、箱梁表面为无滑移壁面(wall)。自定义函数确定入口TSI阵风风速。
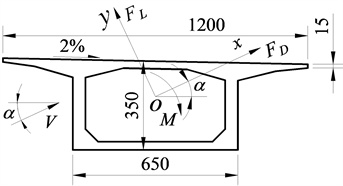
Figure 1. The section of box girder (unit: cm)
图1. 箱梁断面(单位:cm)

Figure 2. Numerical simulation domain
图2. 数值模拟计算域
2.3. 气动力
定义风轴坐标系下均匀来流风速U以风攻角 作用时的箱梁断面的阻力系数 、升力系数 和力矩系数 :
(3a)
(3b)
(3c)
式中,B为箱梁断面的计算宽度,取 ;L为箱梁的节段长度,此处为二维断面,取 ; 为空气密度,取 ; 、 和 分别为风轴坐标系下作用在箱梁断面上的阻力、升力和力矩(箱梁断面形心为扭转中心) (如图1),均取非定常计算结果的平均值。
定义风轴坐标系下TSI阵风以风攻角 作用时箱梁断面的阻力系数 、升力系数 和力矩系数 :
(4a)
(4b)
(4c)
式中, 、 和 分别为t时刻箱梁断面的阻力、升力和力矩,其正方向同图1所示的均匀来流作用下的静力三分力。
根据准定常假设,TSI阵风作用下箱梁断面的阻力系数、升力系数和力矩系数的参考值 、 和 与均匀来流作用下的静力三分力系数存在如下关系:
(5a)
(5b)
(5c)
3. 数学模型
3.1. 控制方程
采用有限体积法求解基于Boussineq涡黏性模型的二维非定常不可压缩雷诺平均N-S方程:
(6a)
(6b)
(6c)
式中, 为空气密度,取 ;u和v分别为流体沿x和y坐标轴方向的速度;t为计算时间; ,p为空气静压,k为湍流动能; , 为空气的动力黏性系数,取 , 为空气的湍流黏性系数。
k和 由RNG k-ε湍流模型的运输方程 [11] 确定:
(7a)
(7c)
式中, 和 分别代表k和 的逆有效Prandtl常数; 代表平均应变率对湍流耗散率 的影响; 、 和 的详细定义参见文献 [11] [12]。高雷诺数( )下, 。本文采用的湍流模型常数:
, , , , , , 。
3.2. 计算网格及时间步长
以风攻角 为例,由图3所示的3种网格计算均匀来流风速 作用下箱梁断面的静力三分力系数,对比分析计算结果后确定TSI阵风分析的计算网格。采用四边形结构化网格对计算域进行网格划分,其中贴体网格高度根据文献 [12] [13] 确定。网格1的总网格数量为62,828,贴体网格高度为1.0 mm,计算得到 。网格2在网格1基础上对尾流区域进行了网格加密,总网格数量为64,351。网格3进一步将贴体网格高度减小到0.5 mm,并对箱梁表面附近区域进行了网格加密,总网格数量为109,060。采用迭代时间步长0.0001 s计算得到的3种网格下的箱梁断面的静力三分力系数差别不大,与风洞试验结果 [10] 对比如表1所示。网格1可以满足计算精度要求。因此,采用网格1的方式对其余风攻角下的计算域进行网格划分。
 (a) Grid 1
(a) Grid 1
 (b) Grid 2
(b) Grid 2
 (c) Grid 3
(c) Grid 3
Figure 3. Local meshes of three gird schemes
图3. 3种网格局部图
Table 1. Comparison of the CFD results and wind tunnel test data of static coefficients of aerodynamic forces
表1. CFD静力三分力系数与风洞试验结果对比
进一步采用网格1,分别以迭代时间步长0.00005 s和0.0005 s计算箱梁断面的静力三分力系数。计算结果及相对于风洞试验结果的误差如表2所示。可以看到,将迭代时间步长增大到0.0005 s后,CFD数值计算的精度并没有受到明显的影响。因此,本文的CFD计算均采用迭代时间步长0.0005 s。
Table 2. Numerical results of static coefficients of aerodynamic forces at different iteration time steps
表2. 不同迭代时间步长的静力三分力系数计算结果
4. 箱梁断面的静力三分力系数验证
均匀来流风速 以风攻角 作用,计算得到箱梁断面的静力三分力系数总体上大于风洞试验结果 [10],相对误差20%左右,如表3所示。计算误差可能来源于箱梁表面附近的气流分离和再附,以及旋涡的脱落使得流场比较复杂,影响了CFD数值计算的精度。RNG k-ε湍流模型及计算条件也限制了计算精度。CFD计算结果总体上满足箱梁断面气动力的分析要求。
Table 3. Comparison of CFD results and wind tunnel data of static coefficients of aerodynamic forces
表3. CFD计算的静力三分力系数与风洞试验结果的对比
5. TSI阵风作用下箱梁断面的气动力及流场特性
5.1. 箱梁断面的气动力特性
当TSI阵风以风攻角
作用时,CFD计算得到的阻力系数
、升力系数
和力矩系数
总体上分别围绕参考值
、
和
小幅波动,但较大风攻角时三分力系数的波动幅度较大。以
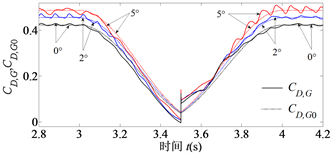
风攻角为例,CFD计算得到的阻力系数、升力系数和力矩系数时程曲线分别如图4~6所示。TSI阵风作用下箱梁断面的气动力有以下基本特性。1) TSI阵风作用下的阻力与准定常假设的阻力基本一致,但负攻角较大时阻力系数波动幅度较大,如图4(c)所示。在风速的峰/谷值时刻
后,阻力系数时程曲线
存在明显的跳跃现象,如图4所示。其原因在于
时刻风速的导数
的理论值不存在。理论上,CFD迭代计算的时间步长越小,这种跳跃现象越明显。当风速
且风速减小到风速谷值附近时,存在轻微的负阻力现象,如图4(b)和图4(d)所示。2) 正/负风攻角较大时,阻力和升力系数时程的波动幅度较大。在风速
的区段,即
,攻角
的阻力系数
和攻角
的升力系数 的波动幅度较大。但在风速
的波动幅度较大。但在风速 的区段,即
的区段,即 ,三分力系数时程曲线在风速谷值附近均有波动幅度减小趋势。3) TSI阵风作用下升力系数
,三分力系数时程曲线在风速谷值附近均有波动幅度减小趋势。3) TSI阵风作用下升力系数 变化滞后于阵风风速变化。在
变化滞后于阵风风速变化。在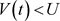 的区段,风速由谷值逐步增大的初始阶段,升力系数
的区段,风速由谷值逐步增大的初始阶段,升力系数 明显小于
明显小于 ;在风速上升的末段,升力系数
;在风速上升的末段,升力系数 相对于
相对于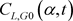 有一定程度的偏离,如图5(b)、图5(d)。4) 风攻角较小时,在风速
有一定程度的偏离,如图5(b)、图5(d)。4) 风攻角较小时,在风速 区段的风速上升末段力矩系数
区段的风速上升末段力矩系数 明显大于
明显大于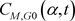 ,如图6(b)、图6(d)。
,如图6(b)、图6(d)。
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
(a) 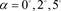 and
and 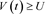
(b) 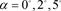 and
and 
(c) 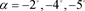 and
and 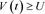
(d)  and
and 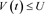
Figure 4. Time history of the coefficient of drag in TSI gusty wind
图4. TSI阵风作用下的阻力系数时程曲线
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
(a) 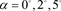 and
and 
(b)  and
and 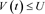
(c)  and
and 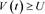
(d)  and
and 
Figure 5. Time history of the coefficient of lift in TSI gusty wind
图5. TSI阵风作用下的升力系数时程曲线
5.2. 箱梁断面的绕流流场特性
以风攻角 为例,TSI阵风作用下计算得到的流场静压分布如图7 (仅显示箱梁附近计算区域
为例,TSI阵风作用下计算得到的流场静压分布如图7 (仅显示箱梁附近计算区域
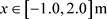 ,
,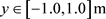 )所示。箱梁断面的气动力计算仅考虑箱梁表面的静压的相对值,故流
)所示。箱梁断面的气动力计算仅考虑箱梁表面的静压的相对值,故流
场入口的初始静压设置为零,出口设置为压力出口并且固定静压为0 Pa。在风速大于均匀来流的时段
( ),箱梁表面的远场静压随计算时间增大而增大。当入口风速由10 m/s逐步增大到最大值17 m/s时(
),箱梁表面的远场静压随计算时间增大而增大。当入口风速由10 m/s逐步增大到最大值17 m/s时( ),CFD计算得到的入口静压由0 Pa逐渐增大到约245 Pa。当入口风速达到最大值
),CFD计算得到的入口静压由0 Pa逐渐增大到约245 Pa。当入口风速达到最大值
17 m/s后,再计算1个迭代时间步,入口静压急剧下跌到约−480 Pa;然后,入口风速逐步减小到10 m/s
时(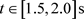 ),入口静压由约−238 Pa逐步增大到0 Pa。入口静压的跳跃正是前述箱梁断面的阻力系数在
),入口静压由约−238 Pa逐步增大到0 Pa。入口静压的跳跃正是前述箱梁断面的阻力系数在 跳跃的原因。在阵风风速小于均匀来流的时段(
跳跃的原因。在阵风风速小于均匀来流的时段(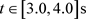 ),箱梁表面的远场静压随计算时
),箱梁表面的远场静压随计算时
间增大而减小。当入口风速由10 m/s逐步减小到最小值3 m/s时,CFD计算得到的入口静压由0 Pa逐渐减小到约−242 Pa。当入口风速达到最小值 3 m/s后,再计算1个迭代时间步,入口静压急剧增加到约482 Pa;
然后,入口风速由最小值3 m/s逐步增大到10 m/s时( )时,入口静压由约242 Pa逐步减小到
)时,入口静压由约242 Pa逐步减小到
0 Pa。此处的入口静压跳跃也是前述箱梁断面的阻力系数在 跳跃的原因。
跳跃的原因。
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
(a) 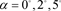 and
and 
(b)  and
and 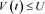
(c) 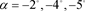 and
and 
(d) 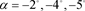 and
and 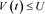
Figure 6. Time history of the coefficient of moment in TSI gusty wind
图6. TSI阵风作用下的力矩系数曲线
 (a)
(a)
 (b)
(b)
 (c)
(c)
 (d)
(d)
 (e)
(e)
 (f)
(f)
(a) (b)
(b) 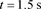 (c)
(c) (d)
(d)  (e)
(e)  (f)
(f) 
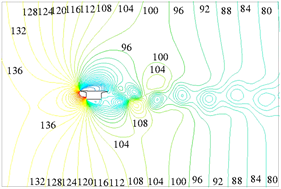
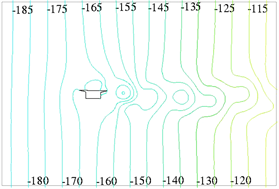
Figure 7. Static pressure distribution at angle of attack of 0˚ (unit: Pa)
图7. 0˚风攻角静压分布(单位:Pa)
在风速增大时段(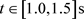 ,
, ),从入口到出口的流场静压整体上由正压逐渐减少到0 Pa,形成顺压梯度
),从入口到出口的流场静压整体上由正压逐渐减少到0 Pa,形成顺压梯度 ,造成箱梁表面的阻力增加;在风速减小时段(
,造成箱梁表面的阻力增加;在风速减小时段( ,
, ),
),
从入口到出口的流场静压整体上由负压逐渐增加0 Pa,形成逆压梯度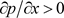 ,造成箱梁表面的阻力减小。流场静压的总体特点与N-S方程的分析结果一致,但入口静压在TSI阵风风速峰/谷值时刻发生跳跃
,造成箱梁表面的阻力减小。流场静压的总体特点与N-S方程的分析结果一致,但入口静压在TSI阵风风速峰/谷值时刻发生跳跃
可能不真实。在风速大于均匀来流风速的时段(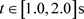 ),TSI阵风使得箱梁的尾流旋涡增强了;而在阵风风速小于均匀来流风速的时段(
),TSI阵风使得箱梁的尾流旋涡增强了;而在阵风风速小于均匀来流风速的时段(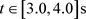 ),TSI阵风使得箱梁的尾流旋涡减弱了。其余风攻角
),TSI阵风使得箱梁的尾流旋涡减弱了。其余风攻角
下的静压分布的计算结果类似,除风攻角绝对值较大时,箱梁的尾流旋涡更强外。
箱梁尾流旋涡分布特点可以进一步从图8所示的0˚和+5˚风攻角下的速度分布对比图中看到。
 (a)
(a)
 (b)
(b)
(a) (b)
(b) 
Figure 8. Comparison of velocity distribution at angles of attack of 0˚ and +5˚ at (unit: m/s)
(unit: m/s)
图8. 0˚和+5˚攻角在  时的速度分布对比(单位:m/s)
时的速度分布对比(单位:m/s)
6. 结论
本文采用RNG k-ε湍流模型模拟分析了TSI阵风以不同风攻角作用过程中箱梁断面的气动力及流场特性。分析得到以下主要结论:1) TSI阵风作用过程中箱梁断面的气动力总体上围绕准定常假设的气动力作小幅波动,但风攻角较大时气动力波动幅度较大。2) CFD计算得到的TSI阵风作用过程中箱梁断面的阻力系数在TSI阵风风速峰/谷值时刻存在跳跃、升力系数变化滞后于TSI阵风风速变化、流场整体静压存在顺压和逆压梯度等。TSI阵风模型应用于箱梁的气动力数值模拟存在局限性,将在后续的CFD数值模拟中改进。
基金项目
四川省教育厅重点项目(立项编号:17ZA0367)、西华大学校重点项目(项目编号:Z1520610)、国家自然科学基金面上项目(项目编号:51378442)资助。
文章引用
黄 菲,黄 林,周俊吉. TSI阵风作用下箱梁断面的气动特性分析
Aerodynamic Characteristic Analysis of Box Girder Section in TSI Gusty Wind[J]. 建模与仿真, 2020, 09(01): 19-28. https://doi.org/10.12677/MOS.2020.91003
参考文献
- 1. 同济大学. JTG/T 3360-01-2018公路桥梁抗风设计规范[S]. 北京: 人民交通出版社股份有限公司, 2018.
- 2. 陈艾荣, 黄鹏, 项海帆. 桥梁阵风风速系数研究[J]. 同济大学学报, 1998, 26(3): 241-244.
- 3. Xu, Y.L. and Ding Q.S. (2006) Interaction of Railway Vehicles with Track in Cross-Winds. Journal of Fluids and Structures, 22, 295-314. https://doi.org/10.1016/j.jfluidstructs.2005.11.003
- 4. BSI Standards Limited (2018) BS EN 14067-6 Railway Applications-Aerodynamics, Part 6: Requirements and Test Procedures for Cross Wind Assessment.
- 5. Proppe, C. and Wetzel, C. (2010) A Probabilisitic Approach for Assessing the Crosswind Stability of Ground Vehicles. Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 48, 411-428. https://doi.org/10.1080/00423114.2010.482158
- 6. 曹亚博, 凌亮, 邓永权, 等. 强阵风环境下高速列车运行安全性研究[J]. 机械工程学报, 2013, 49(18): 30-37.
- 7. 吴超, 杜礼明. 瞬态风场下带风屏障的高架桥上高速列车气动特性[J]. 大连交通大学学报, 2017, 38(2): 21-26.
- 8. Taylor, G.I. (1938) The Spectrum of Turbulence. Pro-ceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 164, 476-490. https://www.jstor.org/stable/97077 https://doi.org/10.1098/rspa.1938.0032
- 9. Carrarini, A. (2006) Relia-bility Based Analysis of the Crosswind Stability of Railway Vehicles. Ph.D. Thesis, Technical University of Berlin, Berlin.
- 10. 刘钥, 陈政清, 张志田. 箱梁断面静风力系数的CFD数值模拟[J]. 振动与冲击, 2010, 29(1): 133-137.
- 11. Yakhot, V. and Orszag, S.A. (1986) Renormalization Group Analysis of Turbulence I. Basic Theory. Journal of Scientific Computing, 1, 3-51. https://doi.org/10.1007/BF01061452
- 12. 黄林. 计算流体力学在桥梁风工程中的应用研究[M]. 成都: 西南交通大学出版社, 2017.
- 13. Huang, L., Liao, H.L., Wang, B., et al. (2009) Numerical Simulation for Aerodynamic Derivatives of Bridge Deck. Simulation Modelling Practice and Theory, 17, 719-729. https://doi.org/10.1016/j.simpat.2008.12.004
NOTES
*通讯作者。
