Statistical and Application
Vol.3 No.04(2014), Article ID:14463,6 pages
DOI:10.12677/SA.2014.34019
Generalized Skew t Distribution of Log-Return Rate in Stock Market
Department of Mathematics, Guilin University of Aerospace Technology, Guilin
Email: xinyang_emily@sina.cn
Copyright © 2014 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Sep. 12th, 2014; revised: Oct. 11th, 2014; accepted: Oct. 20th, 2014
ABSTRACT
The main aim of this paper is to study the distribution characteristics of log-return rate in stock market. The closing data of a year trading day of the 6 indexes (the Shanghai composite index, Shenzhen stock index, industrial index, real estate index, consumer services index, and food and beverage index), are done with the empirical analysis by using the statistical methods. Results show that the log-return rates of the stock indexes do not obey the normal distribution, with the characteristics of high peak, heavy tail and skew distribution. And results also show that the log-return rates are with high probability to be accepted as obeying the generalized skew t distribution. So the generalized skewed t distribution is a reasonable distribution to research the log-return rate of stock market.
Keywords:Stock Index, Log-Return Rate, Generalized Skewed t Distribution

证券市场对数收益率的
广义偏斜t分布
杨 昕
桂林航天工业学院,数理部,桂林
Email: xinyang_emily@sina.cn
收稿日期:2014年9月12日;修回日期:2014年10月11日;录用日期:2014年10月20日

摘 要
本文的主要问题是研究证券市场中对数收益率的分布特征。对上证指数、深证成指、工业指数、地产指数、消费服务和食品饮料等6个指数一个年度的交易日的收盘数据,利用统计检验方法进行实证分析,分析结果表明:证券指数的对数收益率不服从正态分布,具有尖峰、厚尾、偏斜等特征,它们均以较大的概率被接受为服从广义偏斜t分布,所以广义偏斜t分布是研究证券市场对数收益率的合理分布。
关键词
证券指数,对数收益率,广义偏斜t分布

1. 引言
对数收益率是研究证券市场中一个重要变量,用它可以研究证券投资组合和相应的投资风险管理。例如,马柯维茨的均值-方差投资组合理论,威廉·夏普(William F Sharpe)的资本资产定价模型CAPM,都是建立在证券对数收益率的基础上。又如,在证券风险管理中利用证券投资组合的对数收益率的风险在值VaR (Value at Risk),条件风险在值CVaR(Conditional Value at Risk),都是用来刻画投资风险。
为了这些研究和相应理论的需要,人们通常假设对数收益率服从正态分布(Duffie and Pan [1] 1997)。然而,有许多实际数据说明证券市场的对数收益率不服从正态分布(Mandelbrot
[2] 1963, Fama [3] 1965,Blattberg and Gonedes [4] 1974, Cont [5] 2001),其分布通常具有尖峰、厚尾、偏斜和非对称等特点。因此,人们假设或检验对数收益率服从其它非正态分布,并以此研究证券市场的各种问题。可选择的分布有: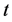 分布(Seneta [6] 2004, Lin et al. [7] 2006, Fergusson and
Platen [8] 2006),幂律分布(Wu [9] 2006, Klass [10] 2007, Plerou and Stanley [11] 2008),Laplace分布(刘建元和刘琼荪[12]
2007,宋丽娟和杨虎[13] 2008,陈晔等人[14] 2010),等等。
分布(Seneta [6] 2004, Lin et al. [7] 2006, Fergusson and
Platen [8] 2006),幂律分布(Wu [9] 2006, Klass [10] 2007, Plerou and Stanley [11] 2008),Laplace分布(刘建元和刘琼荪[12]
2007,宋丽娟和杨虎[13] 2008,陈晔等人[14] 2010),等等。
大家知道,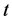 分布是尖峰厚尾对称分布,幂律分布是厚尾非对称分布,Laplace分布的厚尾性是处在正态分布与
分布是尖峰厚尾对称分布,幂律分布是厚尾非对称分布,Laplace分布的厚尾性是处在正态分布与 分布之间的尖峰厚尾对称分布。我们注意到偏斜
分布之间的尖峰厚尾对称分布。我们注意到偏斜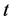 分布同时具有尖峰、厚尾、偏斜和非对称等特点,因此本文重点研究偏斜
分布同时具有尖峰、厚尾、偏斜和非对称等特点,因此本文重点研究偏斜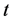 分布,在Azzalini [15] (1985)、Nadarajah
and Kotz [16] (2007)和Nadarajah [17] (2009)等人对标准偏斜
分布,在Azzalini [15] (1985)、Nadarajah
and Kotz [16] (2007)和Nadarajah [17] (2009)等人对标准偏斜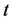 分布定义的基础上,我们考虑一种广义偏斜t分布(见文中定义2),对上证指数、深证成指、工业指数、地产指数、消费服务、食品饮料等6个指数的实际数据,利用极大似然方法估计分布参数,检验这些指数数据的分布,研究证实这6个指数的对数收益率都服从广义偏斜
分布定义的基础上,我们考虑一种广义偏斜t分布(见文中定义2),对上证指数、深证成指、工业指数、地产指数、消费服务、食品饮料等6个指数的实际数据,利用极大似然方法估计分布参数,检验这些指数数据的分布,研究证实这6个指数的对数收益率都服从广义偏斜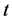 分布。
分布。
2. 广义偏斜t分布的定义
Azzalini [15] (1985)首先提出偏斜正态分布(skew-normal distribution)的概念,其理论依据是如下引理。
引理1 设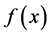 是关于原点对称的密度函数,
是关于原点对称的密度函数, 是绝对连续分布函数,其导数
是绝对连续分布函数,其导数 关于原点对称,则对于任意的实数
关于原点对称,则对于任意的实数![]() ,函数
,函数
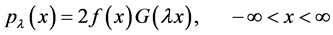 (1)
(1)
是一个密度函数。
利用引理1可以定义各种偏斜分布(Azzalini [15] 1985,Nadarajah和Kotz [16] 2007,Nadarajah [17] 2009),如偏斜正态分布、偏斜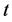 分布、偏斜柯西分布、偏斜Logistic分布、偏斜Laplace分布,等等。其中偏斜
分布、偏斜柯西分布、偏斜Logistic分布、偏斜Laplace分布,等等。其中偏斜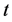 分布定义如下:
分布定义如下:
定义1 设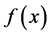 是自由度为
是自由度为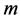 的
的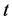 分布的密度函数,即
分布的密度函数,即
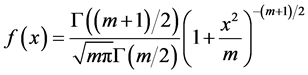 ,(2)
,(2)
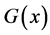 是
是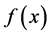 相应的分布函数,则由(1)式确定的密度函数的分布称为偏斜
相应的分布函数,则由(1)式确定的密度函数的分布称为偏斜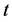 分布(skew t distribution),其自由度为
分布(skew t distribution),其自由度为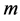 ,偏斜参数为
,偏斜参数为![]() ,并记为
,并记为 。
。
Nadarajah和Kotz [16] (2007)研究了偏斜 分布
分布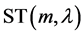 的密度函数的表示,以及矩的计算公式。
的密度函数的表示,以及矩的计算公式。
在偏斜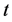 分布
分布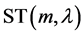 中,自由度参数
中,自由度参数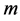 是反映分布的厚尾特征,自由度
是反映分布的厚尾特征,自由度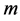 愈小分布的尾部愈厚,自由度
愈小分布的尾部愈厚,自由度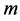 愈大分布的尾部愈轻;参数
愈大分布的尾部愈轻;参数![]() 是反映分布的偏斜方向和偏斜程度,当
是反映分布的偏斜方向和偏斜程度,当![]() 时分布重心偏右,当
时分布重心偏右,当![]() 时分布重心偏左,
时分布重心偏左,![]() 的绝对值愈大偏斜程度愈大。显然,这个分布还缺少两个参数,一个是位置参数
的绝对值愈大偏斜程度愈大。显然,这个分布还缺少两个参数,一个是位置参数![]() ,另一个尺度参数
,另一个尺度参数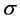 ,这会影响它在实际应用中的适应性。因此,本文考虑使用如下广义的偏斜
,这会影响它在实际应用中的适应性。因此,本文考虑使用如下广义的偏斜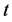 分布。
分布。
定义2 设随机变量![]() 服从定义1所定义的偏斜
服从定义1所定义的偏斜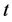 分布
分布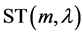 ,令
,令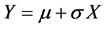 ,称随机变量
,称随机变量 服从广义偏斜
服从广义偏斜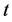 分布,记为
分布,记为 ,其中位置参数
,其中位置参数![]() ,尺度参数
,尺度参数![]() 。
。
广义偏斜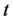 分布
分布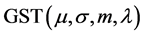 的密度函数为
的密度函数为
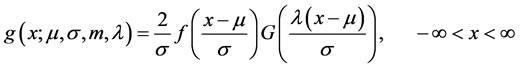 (3)
(3)
其中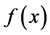 和
和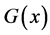 分别是自由度为
分别是自由度为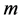 的
的 分布
分布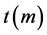 的密度函数和分布函数。显然,广义偏斜
的密度函数和分布函数。显然,广义偏斜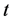 分布具有如下基本性质。
分布具有如下基本性质。
性质1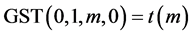 。
。
性质2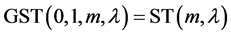 。
。
3. 广义偏斜t分布的参数估计
广义偏斜 分布
分布 有四个参数,可以利用极大似然估计方法估计,其似然函数为
有四个参数,可以利用极大似然估计方法估计,其似然函数为
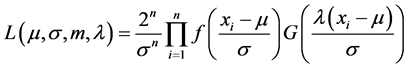 , (4)
, (4)
其中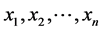 是样本数据。相应的对数似然函数为
是样本数据。相应的对数似然函数为
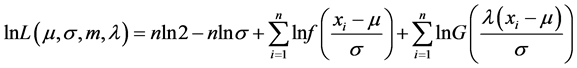 . (5)
. (5)
通过极大化对数似然函数(5)式可以计算出参数的估计值,在具体计算中我们是利用R软件中的非线性极小化nlm函数(Non-Linear Minimization)。注意对数似然函数极大化等价于对负的对数似然函数极小化,所以这个函数nlm可以对极小化和极大化进行求解。
4. 证券指数对数收益率的分布检验
4.1. 证券指数的样本数据
本文选择上证指数、深证成指、工业指数、地产指数、消费服务、食品饮料等6个指数作为研究对象,对这些指数收集从2012年7月至2013年6月完整一年时间共239个交易日的收盘价数据。设 表示某证券指数在第
表示某证券指数在第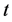 日的收盘指数,则
日的收盘指数,则 就是该指数在第t日的对数收益率,下面将讨论这些对数收益率的分布特征。
就是该指数在第t日的对数收益率,下面将讨论这些对数收益率的分布特征。
4.2. 对数收益率的正态性检验
正态性检验有多种方法,这里考虑利用偏度(Skewness)检验、峰度(Kurtosis)检验和夏皮洛-威尔克(Shapiro-Wilk)检验,计算结果见表1。从偏度检验看,深证成指、工业指数和地产指数等3个指数的偏度检验P值都小于0.05,说明有显著的偏度;而上证指数、消费服务和食品饮料等3个指数的偏度检验P值都大于0.05,说明没有显著的偏度。从峰度检验看,6个指数的峰度检验P值都远远小于0.01,注意表1中的峰度值(kurtosis)是减了3的,所以这些指数的对数收益率的分布的峰值显著高于正态分布。图1是正态分布拟合曲线图,它更直观地看出这些指数的对数收益率的直方图分布的峰值显著高于正态分布。另外,从Shapiro-Wilk正态性检验看,所有指数的检验P值也都远远小于0.01,这说明它们与正态分布有非常显著的差异。这些统计检验事实表明:这6个证券指数的对数收益率在研究时间段内不服从正态分布。
表1. 偏度检验、峰度检验与Shapiro-Wilk正态性检验
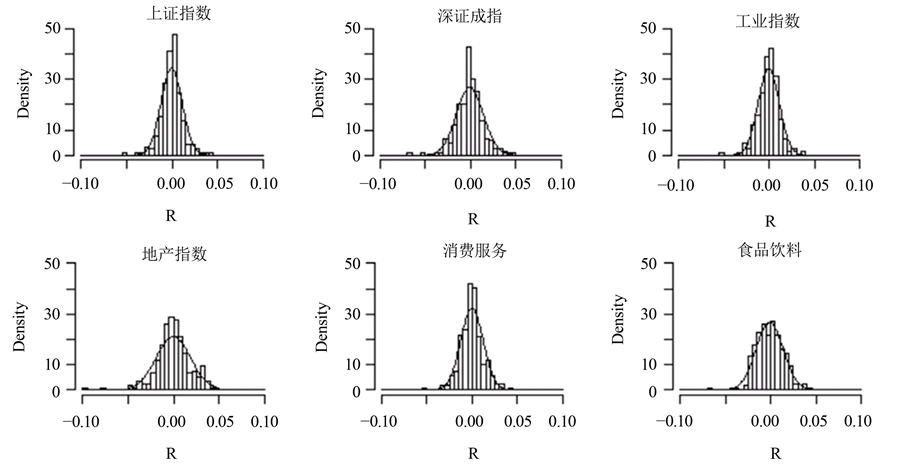
Figure 1. Fitting curve of normal distribution
图1. 正态分布拟合曲线
4.3. 对数收益率的广义偏斜t分布检验
从前面的检验结果和图1知,证券指数的对数收益率具有尖峰、偏斜的特点,所以我们考虑检验它们是否与广义偏斜 分布有较好的拟合,为此做广义偏斜
分布有较好的拟合,为此做广义偏斜 分布的K-S检验。在做检验前,首先要利用极大似然方法估计广义偏斜
分布的K-S检验。在做检验前,首先要利用极大似然方法估计广义偏斜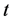 分布的四个参数,然后再计算相应的K-S检验,具体结果见表2。
分布的四个参数,然后再计算相应的K-S检验,具体结果见表2。
从广义偏斜t分布的K-S检验的结果(表2)看,我们有如下结论:
1) P值:所有指数的K-S检验的P值都非常大,前面5个指数(上证指数、深证成指、工业指数、地产指数和消费服务)的P值都大于0.8,最后一个指数食品饮料的P值也接近0.7,这远远大于0.05的概率水平,所以这些指数的对数收益率的分布与广义偏斜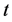 分布没有显著差异,并以较大的概率水平可以接受它们是服从广义偏斜
分布没有显著差异,并以较大的概率水平可以接受它们是服从广义偏斜 分布。
分布。
2)![]() 值:位置参数
值:位置参数![]() 的值都比较小,几乎为零,说明对数收益率是以0为中心左右波动。
的值都比较小,几乎为零,说明对数收益率是以0为中心左右波动。
3) 值:注意到只有当
值:注意到只有当 和
和![]() 时,广义偏斜
时,广义偏斜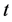 分布才等于标准偏斜
分布才等于标准偏斜 分布,即
分布,即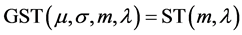 。由于表2中尺度参数
。由于表2中尺度参数 的值远远小于1,所以说明只能用广义偏斜
的值远远小于1,所以说明只能用广义偏斜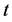 分布
分布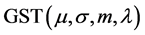 ,而不能用标准偏斜
,而不能用标准偏斜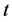 分布
分布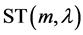 来拟合这些指数的分布。
来拟合这些指数的分布。
4)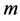 值:前面5个指数(上证指数、深证成指、工业指数、地产指数和消费服务)的自由度都在4左右,自由度比较小,说明它们确实具有比较厚尾的特征。最后一个指数食品饮料的自由度为13.266127,这个自由度稍微大一些,说明该指数的尾部分布与正态分布没有显著差异,并且其峰度值1.029707(见表1)也是这6个指数中最小一个,所以该指数的分布稍微接近正态分布。
值:前面5个指数(上证指数、深证成指、工业指数、地产指数和消费服务)的自由度都在4左右,自由度比较小,说明它们确实具有比较厚尾的特征。最后一个指数食品饮料的自由度为13.266127,这个自由度稍微大一些,说明该指数的尾部分布与正态分布没有显著差异,并且其峰度值1.029707(见表1)也是这6个指数中最小一个,所以该指数的分布稍微接近正态分布。
5)![]() 值:上证指数、工业指数和地产指数的偏斜参数是负值,它们的分布向左偏斜,向左偏斜最大的是工业指数的分布。深证成指、消费服务和食品饮料的偏斜参数是正值,它们的分布向右偏斜,其中消费服务和食品饮料的分布向右偏斜较大。
值:上证指数、工业指数和地产指数的偏斜参数是负值,它们的分布向左偏斜,向左偏斜最大的是工业指数的分布。深证成指、消费服务和食品饮料的偏斜参数是正值,它们的分布向右偏斜,其中消费服务和食品饮料的分布向右偏斜较大。
我们将相应的广义偏斜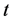 分布的密度展示在图2中,图中直观显示了广义偏斜
分布的密度展示在图2中,图中直观显示了广义偏斜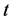 分布比正态曲线更好拟合数据的直方图分布。
分布比正态曲线更好拟合数据的直方图分布。
我们注意到:除了偏斜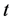 分布外,常见的偏斜分布还有偏斜正态分布、偏斜Logistic分布、偏斜Laplace分布、Pareto分布、指数分布等。关于偏斜正态分布、偏斜Logistic分布和偏斜Laplace分布,这三个分布的两边尾部都是以不低于指数衰减速度
分布外,常见的偏斜分布还有偏斜正态分布、偏斜Logistic分布、偏斜Laplace分布、Pareto分布、指数分布等。关于偏斜正态分布、偏斜Logistic分布和偏斜Laplace分布,这三个分布的两边尾部都是以不低于指数衰减速度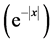 趋于0,均属于轻尾分布,所以这三个分布不太适合于反映对数收益率的尖峰厚尾特征。Pareto分布和指数分布都是属于下方受限分布(即分布的左边尾部是被截尾的分布),这些与对数收益率的两边尾部无限是不相符,也不太适合描述对数收益率的分布。
趋于0,均属于轻尾分布,所以这三个分布不太适合于反映对数收益率的尖峰厚尾特征。Pareto分布和指数分布都是属于下方受限分布(即分布的左边尾部是被截尾的分布),这些与对数收益率的两边尾部无限是不相符,也不太适合描述对数收益率的分布。
广义偏斜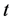 分布具有尖峰、厚尾、偏斜等特征,其尾部是以幂率速度衰减,并且能通过自由度
分布具有尖峰、厚尾、偏斜等特征,其尾部是以幂率速度衰减,并且能通过自由度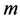 的
的
表2. 广义偏斜t分布的K-S检验
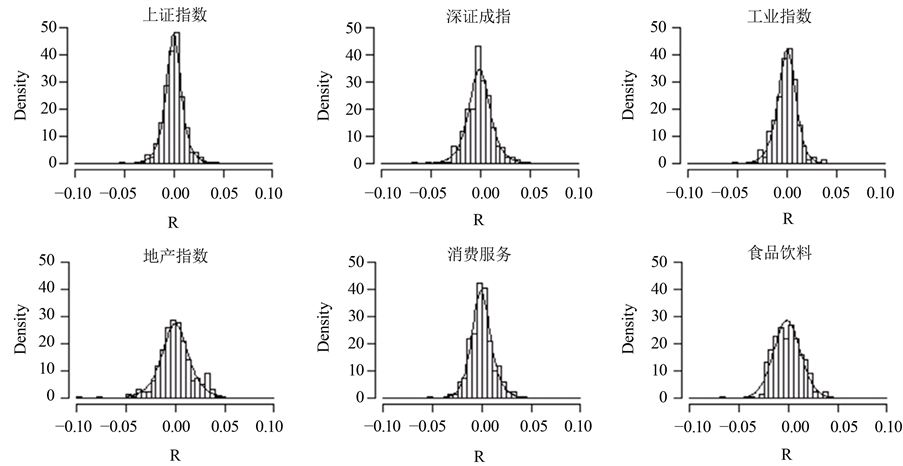
Figure 2. Fitting curve of generalized skewed t distribution
图2. 广义偏斜t分布拟合曲线
大小调节尾部的厚薄程度。另外,通过广义偏斜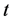 分布的参数
分布的参数![]() ,
,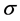 ,
,![]() 可以调节分布的位置、尺度、偏度,从而使其适应更广泛的分布。在实际中,不同的指数可能有不同的分布,广义偏斜
可以调节分布的位置、尺度、偏度,从而使其适应更广泛的分布。在实际中,不同的指数可能有不同的分布,广义偏斜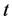 分布能更好地适应这种变化。
分布能更好地适应这种变化。
综合上述讨论,我们认为广义偏斜 分布是拟合这些指数对数收益率分布的合理分布。
分布是拟合这些指数对数收益率分布的合理分布。
5. 结论
本文对上证指数、深证成指、工业指数、地产指数、消费服务和食品饮料等6个指数进行实证分析,利用偏度(Skewness)检验、峰度(Kurtosis)检验和夏皮洛-威尔克(Shapiro-Wilk)检验等方法进行正态性检验,结果表明:证券指数的对数收益率不服从正态分布,具有尖峰、厚尾、偏斜等特征。基于这些特点,我们选择广义偏斜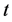 分布
分布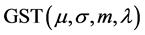 进行拟合对数收益率的分布,通过极大似然估计法和K-S检验法对证券指数对数收益率分布进行拟合与检验,结果表明:这些指数的对数收益率都服从广义偏斜
进行拟合对数收益率的分布,通过极大似然估计法和K-S检验法对证券指数对数收益率分布进行拟合与检验,结果表明:这些指数的对数收益率都服从广义偏斜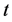 分布,并且接受的概率都很大,这说明广义偏斜
分布,并且接受的概率都很大,这说明广义偏斜 分布是研究证券市场对数收益率的合理分布。
分布是研究证券市场对数收益率的合理分布。
致 谢
非常感谢审稿人和编辑提出修改意见,这些修改意见使本文的内容更加完整和充实。
基金项目
国家自然科学基金项目(11461009),广西自然科学基金项目(2011GXNSFA018133)。
参考文献 (References)
- [1] Duffie, D. and Pan, J. (1997) An overview of value-at-risk. The Journal of Derivatives, 7, 7-49.
- [2] Mandelbrot, B. (1963) The variation of certain speculative pricings. Journal of Business, 36, 394-419.
- [3] Fama, E.F. (1965) The behavior of stock market prices. Journal of Business, 38, 34-105.
- [4] Blattberg, R. and Gonedes, N. (1974) A comparison of stable and student distributions as statistical models for stock prices. Journal of Business, 47, 244-280.
- [5] Cont, R. (2001) Empirical properties of asset returns: Stylized facts and statistical issues. Quantitative Finance, 1, 223- 236.
- [6] Seneta, E.(2004) Fitting the variance-gamma model to financial data. Journal of Applied Probability, 1A, 177-187.
- [7] Lin, S.K., Wang, R.H. and Fuh, C.D. 2006) Risk management for linear and non-linear assets: A Bootstrap method with importance resampling to evaluate Value-at-Risk. Asia-Pacific Finan Markets, 3, 261-295.
- [8] Fergusson, K. and Platen, E. (2006) On the distributional characterization of daily log returns of a world stock index. Applied Mathematical Finance, 13, 19-38.
- [9] Wu, L. (2006) Dampened power law: Reconciling the tail behavior of financial security returns. The Journal of Business, 79, 1445-1473.
- [10] Klass1, O.S., Biham, O., Levy, M., Malcai, O. and Solomon1, S. (2007) The Forbes 400, the Pareto power-law and efficient markets. The European Physical Journal B, 55, 143-147.
- [11] Plerou, V. and Stanley, H.E. (2008) Stock return distributions: tests of scaling and universality from three distinct stock markets. Physical Review E, 77, 037101.1-037101.4.
- [12] 刘建元, 刘琼荪 (2007) 基于非对称Laplace分布研究VaR. 统计与决策, 18, 33-35.
- [13] 宋丽娟, 杨虎 (2008) 基于APARCH-Laplace模型的VaR和CVaR方法. 统计与决策, 14, 16-19.
- [14] 陈晔, 晏小兵, 王跃恒 (2010) 股票投资组合的实证研究. 数学理论与应用, 1, 110-115.
- [15] Azzalini, A. (1985) A class of distributions which includes the normal ones. Scandinavian Journal of Statistics, 12, 171-178.
- [16] Nadarajah, S. and Kotz, S. (2007) Skew models I. Acta Applicandae Mathematicae, 98, 1-28.
- [17] Nadarajah, S. (2009) The skew logistic distribution. AStA—Advances in Statistical Analysis, 93, 187-203.
