Statistical and Application
Vol.04 No.02(2015), Article ID:15509,8
pages
10.12677/SA.2015.42007
The Effects of Different Response Values in Linear Regression Model on Binary Classification
Xiaoying Wang, Yanli Yang, Changlong Chen
School of Mathematics and Physics, North China Electrical Power University, Beijing
Email: yangyanlibang@163.com
Received: Jun. 5th, 2015; accepted: Jun. 20th, 2015; published: Jun. 25th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
We use the multiple linear regression model to deal with the classification problem of two populations. Firstly, we assign the response variables and some corresponding values with certain rules, and then construct discriminant function and criterion via least square method. On this basis, we discuss the effects of different response values on classification for balanced and unbalanced data in linear model. In addition, we compare the mentioned discriminant method above with classic discriminant methods including the classical Mahalanobis distance discriminant and Bayes discriminant. At last, we find the inner relation between these methods as well as their advantages and disadvantages.
Keywords:Binary Classification, Response Values, Discriminant Analysis, Linear Regression Model, Least Square
线性回归模型中响应值的选取 对二分类问题的影响
王小英,杨岩丽,陈常龙
华北电力大学数理学院,北京
Email: yangyanlibang@163.com
收稿日期:2015年6月5日;录用日期:2015年6月20日;发布日期:2015年6月25日

摘 要
我们利用多元线性回归模型处理两个总体的分类问题,首先对响应变量按一定的规则赋值,并在最小二乘法的基础上构建判别函数及判别准则,进而论证了响应值的选取对平衡及不平衡数据二分类问题的影响。此外,我们将此判别方法与经典判别分析方法如:经典马氏距离判别法、Bayes判别法进行比较,并得到它们之间的内在联系及优缺点。
关键词 :二分类问题,响应值选取,判别分析,线性回归模型,最小二乘法

1. 引言
考虑二总体的分类问题,已知有两个总体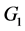 和
和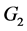 ,且假定
,且假定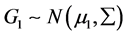 ,
,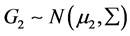 。每个个体有
。每个个体有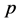 种观测指标,如果进行了
种观测指标,如果进行了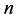 次观测得到的观测矩阵
次观测得到的观测矩阵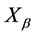 满足:
满足: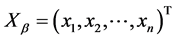 ,这里
,这里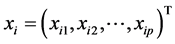 ,
,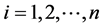 。其中观测矩阵的前
。其中观测矩阵的前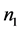 行观测值来自第一个总体
行观测值来自第一个总体 ,第
,第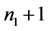 行到第
行到第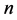 行观测值来自第二个总体
行观测值来自第二个总体 ,且
,且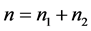 。如今给定一个新的样品,判别分析的目的是根据观测矩阵
。如今给定一个新的样品,判别分析的目的是根据观测矩阵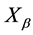 判定此新样品属于两类中的哪一类。
判定此新样品属于两类中的哪一类。
对上述判别分类问题,已有了一些经典的方法,如:距离判别,Bayes判别等。经典马氏距离判别的思想是:新样品距离哪个总体近就判给哪个总体。而Bayes判别的原理是考虑错判损失,依据使总平均损失最小来进行分类判别。其判别准则如下:
当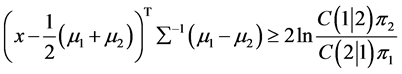 时,
时,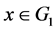 ;否则,
;否则, 。
。
其中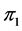 、
、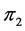 为总体
为总体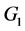 、
、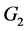 的先验概率;
的先验概率;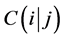 即把本属于总体
即把本属于总体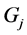 的样品错判给
的样品错判给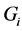 时造成的损失。然而通常情况下,总体参数
时造成的损失。然而通常情况下,总体参数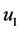 ,
, ,
,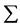 未知,需要由样本数据来估计未知参数。这里我们记:
未知,需要由样本数据来估计未知参数。这里我们记:
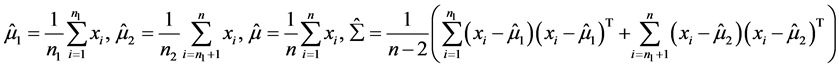
将求得的参数估计值代入判别函数中,可用相应的判别准则对新样品判别归类。当两正态总体协方差阵相等时,我们可根据距离判别和Bayes判别准则导出两个线性判别函数。由判别函数的线性特性及判别函数中指标的多元性,我们考虑多元线性回归模型:
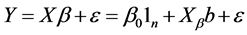 (1.1)
(1.1)
其中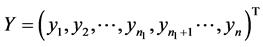 。这里我们按如下规则对响应变量y赋值:
。这里我们按如下规则对响应变量y赋值:
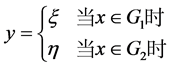 (1.2)
(1.2)
我们不妨令: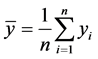 ,
, ,
,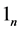 是一个
是一个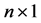 的列向量,其元素全为1。
的列向量,其元素全为1。
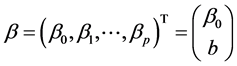 ,
,
张尧庭等[1] 通过讨论回归分析与判别分析的关系指出:可以用回归分析方法来处理判别分析问题,并指出Fishe线性判别函数与线性回归方程(除常数项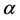 以外)在形式上是一样的;Trevor等[2] 提出了分类的线性方法,并认为最小二乘回归系数与LDA (linear discriminant analysis)中的判别系数成比例;Qing 和Hui [3] 由LDA中的最小二乘公式推导并提出Lassoed判别分析。Jianqing Fan [4] 在A ROAD to Classification in High Dimensional Space中提出了Regularized Optimal Affine Discriminant的判别方法。以上方法都是用线性回归的方法做判别,这涉及到对响应变量y的值的选取问题。张尧庭等[1] 在多元统计分析引论中提出:为了使各类响应值的均值0,不妨令下(1.2)式中的
以外)在形式上是一样的;Trevor等[2] 提出了分类的线性方法,并认为最小二乘回归系数与LDA (linear discriminant analysis)中的判别系数成比例;Qing 和Hui [3] 由LDA中的最小二乘公式推导并提出Lassoed判别分析。Jianqing Fan [4] 在A ROAD to Classification in High Dimensional Space中提出了Regularized Optimal Affine Discriminant的判别方法。以上方法都是用线性回归的方法做判别,这涉及到对响应变量y的值的选取问题。张尧庭等[1] 在多元统计分析引论中提出:为了使各类响应值的均值0,不妨令下(1.2)式中的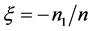 ,
,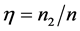 。Trevor等[2] 在文章中令
。Trevor等[2] 在文章中令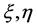 分别为−1,1;而Qing和Hui [3] 则令
分别为−1,1;而Qing和Hui [3] 则令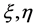 分别为
分别为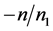 ,
,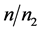 。我们将在前人研究的基础上,进一步讨论回归分析中不同响应值的选取对判别结果的影响。
。我们将在前人研究的基础上,进一步讨论回归分析中不同响应值的选取对判别结果的影响。
2. 用线性回归方法做判别
这里我们将用回归分析的方法来处理判别问题。首先我们对观测数据做中心化处理,如邰淑彩等[5] 中的: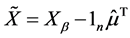 ,
,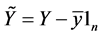 ,得到(1.1)式的一个新的矩阵表达形式:
,得到(1.1)式的一个新的矩阵表达形式:
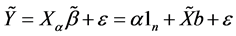 (2.1)
(2.1)
其中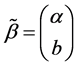 ,
,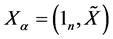 。由多元线性回归模型中系数的最小二乘估计法知:
。由多元线性回归模型中系数的最小二乘估计法知:
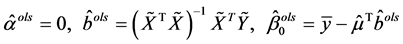 (2.2)
(2.2)
其中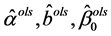 分别是
分别是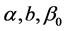 的最小二乘估计。
的最小二乘估计。
Theorem 2.1:在多元线性回归方程(2.1)中,参数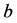 的最小二乘估计
的最小二乘估计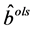 满足式子:
满足式子:
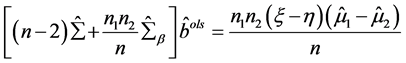 (2.3)
(2.3)
其中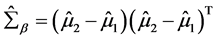 ,特别的,当
,特别的,当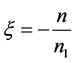 ,
,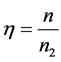 时,
时,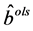 满足如下式子:
满足如下式子:
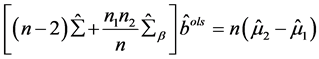
由(2.2)式和(2.3)式,我们将系数的最小二乘估计代入判别函数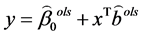 ,并设定判别准则如下(2.4)式,我们用此判别函数及准则对新样本判别归类时能得到下面的定理。
,并设定判别准则如下(2.4)式,我们用此判别函数及准则对新样本判别归类时能得到下面的定理。
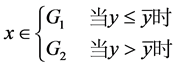 (2.4)
(2.4)
Theorem 2.2:(1) 若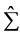 正定,则判别结果只与
正定,则判别结果只与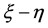 的符号有关,而与
的符号有关,而与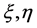 的取值无关。即只要
的取值无关。即只要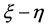 的符号
的符号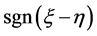 相同,用该方法判别得到的结果就相同,且无论
相同,用该方法判别得到的结果就相同,且无论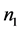 和
和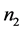 相等与否,该结论都成立。
相等与否,该结论都成立。
(2) 当 且
且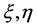 满足
满足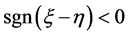 时,用该判别方法与用距离判别法对新样品分类时得到的判别函数及判别结果相同。
时,用该判别方法与用距离判别法对新样品分类时得到的判别函数及判别结果相同。
3. 模拟
3.1. 平衡数据模拟
我们通过数据模拟来验证我们的结论。我们随机生成了两类数据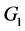 ,
,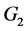 。它们均服从
。它们均服从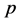 元正态分布,其中
元正态分布,其中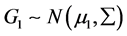 ,
,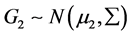 。这里我们取
。这里我们取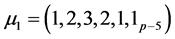 ,
,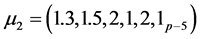 ,
,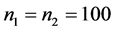 ,
,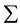 满足:
满足: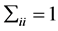 ,
,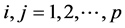
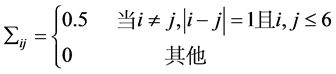 (3.1)
(3.1)
我们采用五折交叉验证的方法,此方法被Breiman等[6] 提议并广泛应用于实际,取数据集的4/5作训练集,剩下的1/5作测试集。然后用训练集拟合判别函数,用测试集评估分类性能。我们分别在 的八种情况下,用距离判别、判别I-III这四种方法对测试集样本判别归类。其中,判别I-III即在Theorem 2.2提出的判别方法中分别取:
的八种情况下,用距离判别、判别I-III这四种方法对测试集样本判别归类。其中,判别I-III即在Theorem 2.2提出的判别方法中分别取: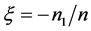 ,
,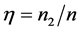 ;
;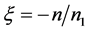 ,
,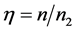 ;
; ,
,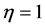 得到的三种判别方法。我们重复模拟试验1000次,最终得到各自的平均错判率如表1。
得到的三种判别方法。我们重复模拟试验1000次,最终得到各自的平均错判率如表1。
显然,在判别I-III中: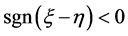 且
且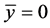 。由表1可知:用判别I-III三种方法判别时的模拟错判率相等,这与Theorem 2.2 (1)相符。此外,当
。由表1可知:用判别I-III三种方法判别时的模拟错判率相等,这与Theorem 2.2 (1)相符。此外,当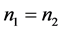 时,用距离判别与用判别I-III这三种方法判别时的模拟错判率相等,满足Theorem 2.2 (2)。此外,我们还可从表格中看出:用以上四种方法对平衡数据
时,用距离判别与用判别I-III这三种方法判别时的模拟错判率相等,满足Theorem 2.2 (2)。此外,我们还可从表格中看出:用以上四种方法对平衡数据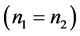 进行判别时,模拟得到的错判率随着维数
进行判别时,模拟得到的错判率随着维数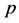 的增加而增加,即判别效果随之降低。
的增加而增加,即判别效果随之降低。
3.2. 不平衡数据模拟
基于上3.1中提到的两类数据,我们分别取p = 10,50,100,并分别在这三种情况下取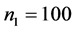 ,
,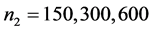 。之后分别用距离判别,Bayes判别,判别I-III这五种方法对前面9种情况做判别,我们重复模拟试验1000次并取平均值,模拟结果如表2。
。之后分别用距离判别,Bayes判别,判别I-III这五种方法对前面9种情况做判别,我们重复模拟试验1000次并取平均值,模拟结果如表2。
这里我们将用一些特定的评价标准评估不同判别方法的分类性能。当数据不平衡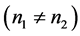 时,Weiss [7] 指出:为提高分类准确率,分类器往往倾向于将新样品预测为多数类而导致少数类样本的识别率较低,所以错判率不能很好的反映判别方法对不平衡数据集的判别效果。因此我们采用不平衡数据集分类中常用的评价标准:F-value [8] 和G-mean [9] 来衡量不同方法判别效果的好坏。这里记:
时,Weiss [7] 指出:为提高分类准确率,分类器往往倾向于将新样品预测为多数类而导致少数类样本的识别率较低,所以错判率不能很好的反映判别方法对不平衡数据集的判别效果。因此我们采用不平衡数据集分类中常用的评价标准:F-value [8] 和G-mean [9] 来衡量不同方法判别效果的好坏。这里记:
 (3.2)
(3.2)
Table 1. The misclassification rate of four discriminant methods
表1. 四种判别方法的错判率比较
Table 2. The discriminant outcome comparison of unbalanced data
表2. 不平衡数据的判别结果比较
其中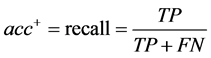 ,
,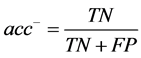 ,
,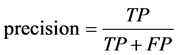 。P:正类(少数类),N:负类(多数
。P:正类(少数类),N:负类(多数
类)。TP与TN分别表示被正确分类的正类和负类样本的数目;FN表示真实类标是正类却被误分为负类的数目,FP表示真实类标是负类而被误分为正类的数目。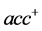 :少数类的查全率,
:少数类的查全率,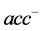 :多数类的查全率,
:多数类的查全率,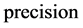 :查准率。陶新民等 [10] 指出:F-Value既考虑了查全率又考虑了查准率,只有在查全率和查准率的值都大时,F-value才会大。同样,只有少数类和多数类样本的查全率同时都大时,G-mean值才会大。因此,F-value和G-mean能综合考虑少数类和多数类两类样本的分类性能,是对不平衡数据分类性能的两个较好的评测指标。
:查准率。陶新民等 [10] 指出:F-Value既考虑了查全率又考虑了查准率,只有在查全率和查准率的值都大时,F-value才会大。同样,只有少数类和多数类样本的查全率同时都大时,G-mean值才会大。因此,F-value和G-mean能综合考虑少数类和多数类两类样本的分类性能,是对不平衡数据分类性能的两个较好的评测指标。
由表2最后三列知:就错判率及不平衡数据的评价标准:F-Value,G-Mean而言,当数据不平衡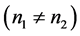 时,判别I-III的判别结果相同且
时,判别I-III的判别结果相同且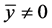 ,此时用距离判别与用判别I-III判别得到的结果不同。
,此时用距离判别与用判别I-III判别得到的结果不同。
此外,当数据的维数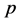 固定不变时,随着数据不平衡程度
固定不变时,随着数据不平衡程度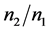 的增加,距离判别及Bayes判别的错判率、F-value和G-mean值变化相对较小,即受不平衡程度的影响较小,判别效果较好;当数据不平衡程度
的增加,距离判别及Bayes判别的错判率、F-value和G-mean值变化相对较小,即受不平衡程度的影响较小,判别效果较好;当数据不平衡程度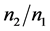 固定不变时,随着维数p的增加,距离判别及Bayes判别得的错判率较低且F-value,G-Mean值较高,判别效果较好;然而我们可以结合线性模型的变量选择方法如:Tibshirani [11] 提出的LASSO (Least Absolute Shrinkage and Selection Operator)、Fan和Li [12] 提出的SCAD (Smoothly Clipped Absolute Deviation)、AIC、BIC及Fan和Lv [13] [14] 提出的SIS (Sure Independence Screening)等方法选择重要变量对数据降维,与此同时,用线性回归的方法对新样品判别归类。用这种方法,我们在降维的同时对数据做判别,可能会使得判别I-III的判别效果得到提高,然而这还有待我们以后做进一步研究。
固定不变时,随着维数p的增加,距离判别及Bayes判别得的错判率较低且F-value,G-Mean值较高,判别效果较好;然而我们可以结合线性模型的变量选择方法如:Tibshirani [11] 提出的LASSO (Least Absolute Shrinkage and Selection Operator)、Fan和Li [12] 提出的SCAD (Smoothly Clipped Absolute Deviation)、AIC、BIC及Fan和Lv [13] [14] 提出的SIS (Sure Independence Screening)等方法选择重要变量对数据降维,与此同时,用线性回归的方法对新样品判别归类。用这种方法,我们在降维的同时对数据做判别,可能会使得判别I-III的判别效果得到提高,然而这还有待我们以后做进一步研究。
3.3. 实例分析
此外,我们对“Wisconsin Diagnostic Breast Cancer (WDBC)”中的真实数据进行了分析。本文采用的数据来源于http://www.datatang.com/data/515。
该数据集包含了关于人体细胞核的30个相关指标(如:细胞核面积、周长、平滑度等)的大量数据,我们从第一类(未患乳腺癌)和第二类(患乳腺癌)的观测样本中各取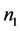 、
、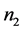 个样品,用五折交叉验证的方法,并分别用距离判别、Bayes判别、判别I-III这五种方法对这
个样品,用五折交叉验证的方法,并分别用距离判别、Bayes判别、判别I-III这五种方法对这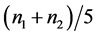 个样品“是否患有乳腺癌”进行分析判别,并得到各自的模拟结果如表3。
个样品“是否患有乳腺癌”进行分析判别,并得到各自的模拟结果如表3。
Table 3. WDBC discriminant result comparison
表3. WDBC判别结果比较
由表3知:由于判别I-III中的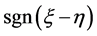 相等,用判别I-III三种方法模拟的判别结果相等。当
相等,用判别I-III三种方法模拟的判别结果相等。当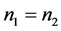 时,距离判别与判别I-III的判别结果相同;当
时,距离判别与判别I-III的判别结果相同;当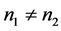 时,它们的判别结果不同。而且,随着不平衡程度
时,它们的判别结果不同。而且,随着不平衡程度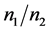 的增加,距离判别及Bayes判别的错判率较低,F-value值较高,受不平衡程度的影响较小,判别效果较好。
的增加,距离判别及Bayes判别的错判率较低,F-value值较高,受不平衡程度的影响较小,判别效果较好。
4. 总结
本文主要研究了线性回归模型中响应值的选取对二分类问题的影响。首先,我们对响应变量按一定的规则赋值,然后用最小二乘法拟合,建立判别函数及判别准则,进而得到以下两个结论:1) 该判别方法下的判别结果只与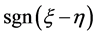 有关,即只要
有关,即只要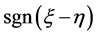 相同,用此判别方法判别的结果就相同。2) 当
相同,用此判别方法判别的结果就相同。2) 当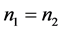 且
且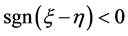 时,用该判别方法得的判别结果与距离判别结果相同。此外,我们用r语言[15] 分别对平衡数据、不平衡数据及真实数据WDBC进行了模拟,得到了与前面两个结论相符的模拟结果。
时,用该判别方法得的判别结果与距离判别结果相同。此外,我们用r语言[15] 分别对平衡数据、不平衡数据及真实数据WDBC进行了模拟,得到了与前面两个结论相符的模拟结果。
基金项目
中央高校基本科研业务费专项资金;北京高等学校青年英才计划项目。
文章引用
王小英,杨岩丽,陈常龙, (2015) 线性回归模型中响应值的选取对二分类问题的影响
The Effects of Different Response Values in Linear Regression Model on Binary Classification. 统计学与应用,02,47-55. doi: 10.12677/SA.2015.42007
参考文献 (References)
- 1. 张尧庭, 方开泰 (1988) 多元统计分析引论. 科学出版社, 北京.
- 2. Hastie, T., Tibshirani, R. and Friedman, J. (2009) Elements of statistical learning: data mining, inference and prediction. 2nd Edition, Springer, Berlin.
- 3. Mai, Q. and Zou, H. (2012) A direct approach to sparse discriminant analysis in ultra-high dimensions. Biometrika, 99, 29-42.
- 4. Fan, J.Q., Feng, Y. and Tong, X. (2012) A road to classification in high dimensional space. Journal of the Royal Statistical Society, Series B, Statistical Methodology, 74, 745-771.
- 5. 邰淑彩, 孙韫玉, 何娟娟 (2005) 应用数理统计(第二版). 武汉大学出版社, 武汉.
- 6. Breiman, L. and Spector, P. (1992) Submodel selection and evaluation in regression: the x-random case. International Statistical Review, 60, 291-319.
- 7. Weiss, G.M. and Provost, F. (2003) Learning when training data are costly: The effect of class distribution on tree induction. Journal of Artificial Intelligence Research, 19, 315-354.
- 8. Kubat, M., Holte, R. and Matwin, S. (1998) Machine learning for the detection of oil spills in satellite radar images. Machine Learning, 30, 195-215.
- 9. Lewis, D. and Gale, W. (1994) Training text classifiers by uncertainty sampling. Proceedings of ACM-SIGIR Conference on Information Retrieval, New York, 73-79.
- 10. 陶新民, 郝思媛, 张冬雪, 徐鹏 (2013) 不均衡数据分类算法的综述. 重庆邮电大学学报(自然科学版), 1, 106- 108.
- 11. Tibshirani, R.J. (1996) Regression shrinkage and selection via the LASSO. Journal of the Royal Statistical Society, Series B, 58, 267-288.
- 12. Fan, J. and Li, R. (2001) Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American Statistical Association, 96, 1348-1360.
- 13. Fan, J. and Lv, J. (2008) Sure independence screening for ultrahigh dimensional feature space (with discussion). Journal of the Royal Statistical Society, Series B, 70, 849-911.
- 14. Fan, J. and Lv, J. (2010) A selective overview of variable selection in high dimensional feature space. Statistica Sinica, 20, 101-148.
- 15. 薛毅, 陈立萍 (2007) 统计建模与R软件. 清华大学出版社, 北京.
附录
Theorem 2.1的证明:由上(2.2)式知: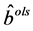 满足式子
满足式子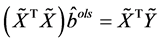 ,即满足
,即满足
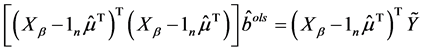 (A.1)
(A.1)
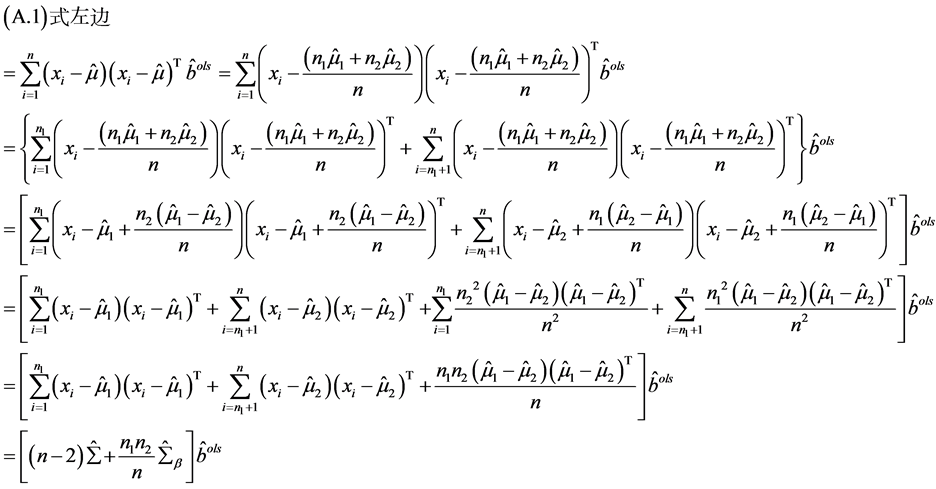
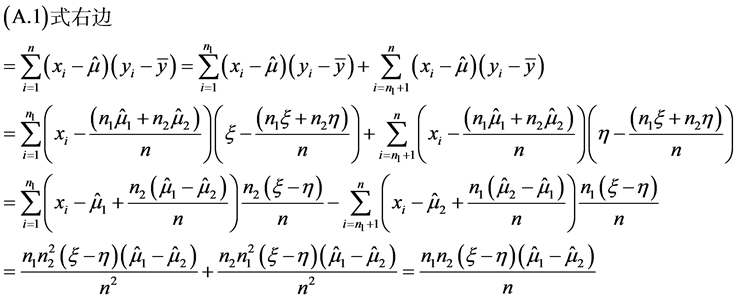
由(A.1)知:左边 = 右边,所以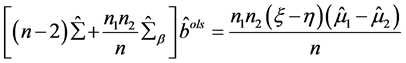 。当
。当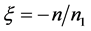 ,
,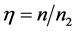 ,
,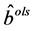 满足式子
满足式子 。
。
Theorem 2.2 (1)的证明:由(2.3)式知:
 (A.2)
(A.2)
此处不妨令
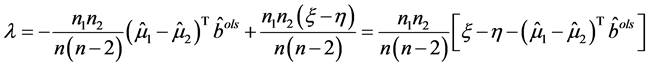 (A.3)
(A.3)
则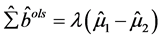 。当
。当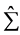 正定时:
正定时: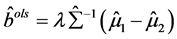 。代入(A.3)式得:
。代入(A.3)式得:
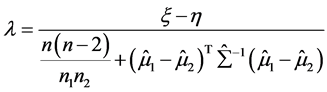 (A.4)
(A.4)
又因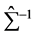 正定,所以
正定,所以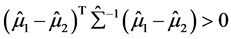 ,因此
,因此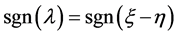 。而且由
。而且由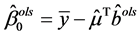 ,
,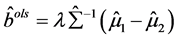 得:
得:
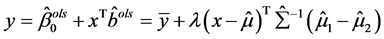 (A.5)
(A.5)
这里令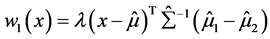 ,则(2.4)式等价于:
,则(2.4)式等价于:
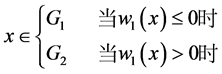 (A.6)
(A.6)
因此,无论 和
和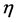 取何值,只要
取何值,只要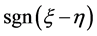 相同,则判别函数相同,用上述方法得到的判别结果相同。Theorem 2.2 (1)得证。
相同,则判别函数相同,用上述方法得到的判别结果相同。Theorem 2.2 (1)得证。
Theorem 2.2 (2)的证明:距离判别的判别函数为:
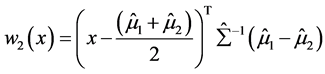 (A.7)
(A.7)
距离判别的判别准则:
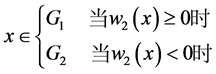 (A.8)
(A.8)
当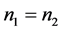 时,
时,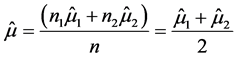 ,即
,即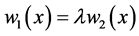 ,且我们前面已证
,且我们前面已证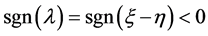 ,所以(A.6)式等价于(A.8)式。因此,当
,所以(A.6)式等价于(A.8)式。因此,当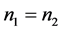 时,用距离判别与用线性回归做判别得到的判别结果相同。
时,用距离判别与用线性回归做判别得到的判别结果相同。
当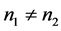 时,
时,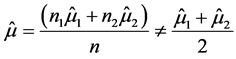 ,此时
,此时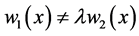 ,用距离判别与用线性回归做判别得到的判别结果不同。Theorem 2.2 (2)得证。
,用距离判别与用线性回归做判别得到的判别结果不同。Theorem 2.2 (2)得证。
