Statistics and Application
Vol.07 No.03(2018), Article ID:25489,8
pages
10.12677/SA.2018.73035
Determination of Cost of Pipe Material in Water Supply and Drainage Pipework
Jiakang Du, Yuqing Li, Hongchun Sun, Qingjun Ren
School of Mathematics and Statistics, Linyi University, Linyi Shandong

Received: May 21st, 2018; accepted: Jun. 7th, 2018; published: Jun. 20th, 2018

ABSTRACT
The relationship between cost of pipe material and pipe size in water supply and drainage pipework is studied in this paper. In order to determine the cost formula of pipe material, we established a liner regression and one-dimensional polynomial regression model and fitted the coefficient of model function by least squares. The effectiveness of the algorithm is verified by numerical experiments.
Keywords:Cost of Pipe Material, Regression Model, Least Squares
给排水管道工程中管材造价的确定
杜家康,李玉卿,孙洪春,任庆军
临沂大学数学与统计学院,山东 临沂

收稿日期:2018年5月21日;录用日期:2018年6月7日;发布日期:2018年6月20日

摘 要
本文通过研究给排水工程中管材造价与管径大小的关系,建立了一元线性回归模型与一元多项式回归模型,利用最小二乘法对模型的系数进行拟合,确定了管材造价与管径大小的公式,最后通过数值实验验证了算法的有效性。
关键词 :管材造价,回归模型,最小二乘法

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
给排水管道工程是与工业生产、社会生活密切相关的工程之一,其工程投资占整个给排水工程投资的较大比重。在施工过程中,不同阶段的水流量大小不同,导致各管段采用的管材口径的大小不同。此外,由于不同口径的管材制作工艺不同,所以同材质的管材造价与管径的关系并不是一个确定的值。特别是随着科学技术的进步,各种新型特种管材纷纷被开发出来 [1]。如何确定管材造价与管径的关系便成为一个非常重要的问题。吴亚群 [2] 利用线性回归模型给出了球墨铸铁管造价公式,不过其中的管材材质,制作工艺都被限制,使得求出的一元线性公式,没办法进一步推广,难以有效的解决实际问题。刘瑞,姚青云,李铁军等人 [3] 管道承压来计算管道造价,给出了一种计算PVC管造价的新方法,但数据搜集相对麻烦,在实际应用时,有很大的弊端。本文利用工程中易于获取到的管径大小与单位长度的管材造价数据,基于实际应用问题,改进线性回归模型,提出利用多项式模型来拟合管径大小与单位长度管径造价的关系函数。最后,通过数据实验算例,证明了此方法的可行性。
2. 求解模型建立
在工程施工过程中,进行造价估算是一件非常重要的事。造价估算对原材料购买,施工队的人数,工程质量把握等都有着举足轻重的参考价值。
假设已知某给排水工程中所用的某种材质的管材的单位造价( )与管材口径的大小( )的价格表以及对应的不同口径的需求量( ),具体信息见表1。施工方已知不同口径管材的需求量( ),要估算本工程中这种管材消耗的资金。假设管材供应商所提供的价格表并不全面,管径大于 的管材造价数据并未给出。问如何利用现有的数据推断出这种管材所消耗的资金M (元)。
首先,已知消耗的资金应该是这种管材不同口径所需资金的总和,目标函数应为:
其次,由于管径大于 的单位管材造价数据未知,所以 未知。不过根据表1中数据,可以
Table 1. Price list of unit cost and diameter of pipe material
表1. 管材的单位造价与管材口径的大小的价格表
假设管材的口径和管材造价之间存在某种隐藏函数关系 。如果这种函数关系存在,目标函数为 。
最后,求出管材口径大小与单位长度管材造价的隐藏的函数关系 ,就能得到总资金M。
2.1. 一元线性回归模型
要考察的一元线形回归模型为
其中x是管材口径大小,y是管材的单位长度造价, 是两个未知参数, 为其他随机因素对y的影响,并且 是不可观察的、均值为0的随机变量。在该模型下,第i组观测值记为 ,是一元线性回归方程的实验值,利用实验值对 作估值。
设有n组观测值: 。将上述观测值代入一元线性回归模型:
使用最小二乘法计算模型中的未知数 。
设函数Q是二元函数。 为偏离真实直线的偏差平方和。记
(1)
求 的估计值 ,使得
(2)
然后(2)式分别对变量 求偏导数,得到这个函数的驻点,用 取代 :
(3)
由(3)式可解得
(4)
其中 。
用上述方法求出得估计值 称为 的最小二乘估计。回归方程为:
其中, 为拟合直线的斜率, 为拟合直线在 的截距,实验值 的几何重心 落在拟合直线上。
2.2. 一元多项式回归
对于已给出的实验值 ,可以构造出m次多项式 [4]
(5)
求多项式的系数 ,使得 的平方和最小,设多项式函数P:
(6)
分别对多元函数P中的每个自变量 求偏导数:
(7)
求多元函数P的驻点,即令 的偏导数都为0:
(8)
对(8)式化简得到:
(9)
可以将(9)式写成矩阵的乘积 [5] :
(10)
(11)
设 , , ,(10)式可以表示为: 。解出多项式回归的系数 就能够得到拟合函数关系:
其中x为不同管径的取值, 为不同管径下的管材造价。
2.3. 模型比较
一元线性回归模型简单易操作,相比多项式而言,所求的变量更少,并且解决方法更加直观,更好理解。但是在拟合的精确度方面,一元线性回归模型不能与多项式模型相比,特别是在比例系数发生变化的情况下,一元线性回归模型只能建立出一个粗略的函数模型。一元多项式回归模型
,
拟合的精度高,能够表示的函数种类多。当 时多项式模型就化为 ,所以可以使用多项式回归模型来表示一元线性回归模型。多项式回归模型的缺点是计算量太大,但利用计算机软件求解,过程将会大大简化,缺点比较容易克服。综上所述,一元多项式回归模型要优于一元线性回归模型。
3. 数值算例
某给排水工程中所用的石墨铸铁管材的单位造价与管材口径的大小的价格和不同口径的需求量均已给出,具体信息见表2。现在施工方已经确定了不同口径的管材的需求量,需要估算工程中这种管材所消耗的资金,但管材供应商所提供的价格表并不全面,管径大于500 mm的单位管材造价数据并未给出。要求利用现有的数据推断出这种管材所消耗的资金 [6]。
首先建立求解消耗资金的目标函数,然后利用回归模型建立单位长度管材造价与管材口径大小的函数关系,将原问题的自变量由管材造价转换为管材口径的大小,最后求解目标函数。
3.1. 具体求解过程
假设管材的口径和管材造价之间存在某种隐藏函数关系 ,可以把目标函数写为 的形式,求出单位管材造价与管材口径的函数关系 即可。
1) 做出散点图
为了简便,计算时以50 mm为一个单位。首先确定回归模型,求出单位管材造价与管材口径的函数关系,利用MATLAB软件作图;如图1所示。
2) 确定数学模型
从散点图我们可以看出,数据近似线性函数,可以选择一元线性回归模型,多项式回归模型。
① 一元线性回归模型。首先设 再设
然后经过(2)~(4)式,求解:
Table 2. Price list of unit cost and diameter of pipe for graphite cast iron pipes
表2. 石墨铸铁管材的单位造价与管材口径的大小的价格表
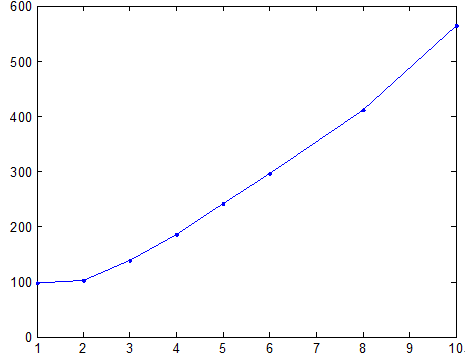
Figure 1. The scatter point diagram of pipe cost and pipe diameter
图1. 管材造价与管材口径的散点连线图
其中 解得
所以一元线性回归模型为
② 多项式回归模型
由于图1近似线性函数,所以多项式回归模型的最高次数为二次即可。设 记 由(6)~(11)式的计算过程,我们可以得到计算的主要数据如下:
,
通过MATLAB软件求解,可得
因此
故 拟合的函数为
3.2. 误差对比分析
利用MATLAB软件做出两种模型分别拟合的函数值与原数据对比图,如图2所示,左边是线性回

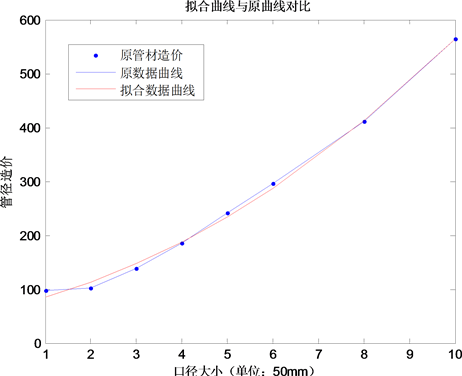
Figure 2. Comparison of two kinds of fitting function values with original data
图2. 两种拟合函数值与原数据对比图

Figure 3. Numerical error contrast diagram of two models
图3. 两种模型的数值误差对比图
归模型拟合的函数值,右边是多项式回归拟合的函数值。
从图2可以看出,线性回归所拟合的函数值与原数据误差一直处于忽大忽小的状态,而多项式回归所拟合的函数值与原数据的误差越来越小,接近于0。通过图3对比两种回归模型对原数据的误差,很直观的看出在本算例中多项式回归模型的误差是远远小于线性回归模型的,这就说明,多项式回归是比线性回归更能拟合出管材口径大小和管材造价所隐藏的函数关系。因此本题采用多项式拟合的结果进行求解。
3.3. 模型代入求解
将拟合的函数为 代入 中,可得
。
通过上面求出的数学模型,施工方只需要知道管径大小(单位:50 mm)以及各自的需求量就能求出这种管材所需要的总资金。
基金项目
大学生创新创业训练计划项目(2018)。
文章引用
杜家康,李玉卿,孙洪春,任庆军. 给排水管道工程中管材造价的确定
Determination of Cost of Pipe Material in Water Supply and Drainage Pipework[J]. 统计学与应用, 2018, 07(03): 297-304. https://doi.org/10.12677/SA.2018.73035
参考文献
- 1. 陈健. 新型塑料给排水管材的特点及应用前景[J]. 山西建筑, 2007, 33(32): 168-170.
- 2. 吴亚群. 树状给水管网的优化设计研究[D]: [硕士学位论文]. 西安: 长安大学, 2014.
- 3. 刘瑞, 姚青云, 李铁军. U-PVC管材造价数值预测模型的研究[J]. 宁夏工程技术, 2011, 10(2): 164-166.
- 4. 赵静, 但琦. 数学建模与数学实验[M]. 北京: 高等教育出版社, 2003: 260-285.
- 5. 余亚冰, 罗磊, 于波. 大型净水厂自动投药系统的建模与研究[J]. 甘肃科学学报, 2012, 24(2): 120-123.
- 6. 白丹. 给水输配水管网系统优化设计研究[D]: [博士学位论文]. 西安: 西安理工大学, 2003.
