Statistics and Application
Vol.
07
No.
05
(
2018
), Article ID:
27182
,
10
pages
10.12677/SA.2018.75058
Research on Robust Optimal Investment and Excess-of-Loss Reinsurance under CEV Model
Bing Li, Caixia Geng
Hebei University of Technology, Tianjin

Received: Sep. 30th, 2018; accepted: Oct. 12th, 2018; published: Oct. 19th, 2018

ABSTRACT
In this paper, we investigate an optimal investment and excess-of-loss reinsurance strategy for an ambiguity-averse insurer (AAI). The financial market consists of one risk-free asset and one risky asset whose price is modeled by a constant elasticity of variance (CEV) model. The insurer can purchase excess-of-loss reinsurance and invest in the financial market. The surplus process of the insurer is approximated by a Brownian motion with drift. The objective is to maximize the minimal expected exponential utility function of the insurer's terminal wealth. By using the dynamic programming approach, we solve the Hamilton-Jacobi-Bellman (HJB) equation and derive the closed form expression of the optimal strategy and the corresponding value function for exponential utility function. Finally, we present numerical examples to illustrate the effects of model parameters on the optimal investment and reinsurance strategies.
Keywords:Robust Control, Excess-of-Loss Reinsurance, Expected Exponential Utility, HJB Equation
CEV模型下鲁棒最优投资和超额损失再保险问题研究
李冰,耿彩霞
河北工业大学,天津

收稿日期:2018年9月30日;录用日期:2018年10月12日;发布日期:2018年10月19日

摘 要
本文研究了一个模糊厌恶保险公司的最优投资和超额损失再保险策略问题。金融市场包含一个无风险资产和一个有风险资产,其中有风险的资产价格服从CEV模型,保险公司可以购买超额损失再保险,并将其盈余投资到金融市场中,且保险公司的盈余过程近似为带漂移的布朗运动。这篇文章的目标是最大化最小最终财富的指数效用函数的期望。通过使用动态规划方法,我们解决了HJB方程并且得到了最优策略以及值函数的表达式。最后,我们用数值例子来说明模型参数对最优策略的影响。
关键词 :鲁棒控制,超额损失再保险,期望指数效用,HIB方程

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
再保险和投资是保险行业的两个核心问题。现如今,保险公司的投资和再保险问题在文献中得到了广泛的研究。例如,Browne [1] 研究了保险公司具有扩散风险模型的最优投资问题,目标是最大化终端财富的效用函数同时最小化破产概率。同Browne [1] 研究的问题相似,Yang和Zhang [2] 研究的是跳扩散风险模型。
据我们所知,风险资产的价格过程一般遵循几何布朗运动,这意味着风险资产价格的波动率是常数的或确定性的函数。而随机波动率是资产模型中的一个重要特征,许多经验也表明风险资产价格的波动率是随机的。近年来,Dias和Nunes [3] 研究了常系数弹性方差扩散下的期权定价。Gu等 [4] ,Gu等 [5] 和Wang等 [6] 研究了在CEV模型下的再保险和投资问题。
我们知道在实践中并不能确定使用哪种模型。因此,模型不确定性成为资产定价和投资组合选择中的一个重要问题。模型的不确定性由一系列概率测度来描述,解决这类问题的一种可行方法是使用鲁棒方法,这导致了许多学者对鲁棒模型的研究。Zhang和Siu [7] 研究了模型不确定的保险公司的最优投资和再保险问题。Branger和Larsen [8] 研究了具有跳跃和扩散风险不确定性的鲁棒投资组合选择。Wang和Li [9] 研究的是随机利率和随机波动率下的鲁棒最优投资策略问题。
与Zheng等 [10] 研究的不同,我们对超额赔款再保险更感兴趣,在大多数情况下,它优于比例再保险。Gu等 [4] 就是研究的超额损失再保险和投资问题,但是没有考虑模型的不确定性。在本文中,保险公司通过购买超额损失再保险和在金融市场中的投资来最大化最小最终财富的指数效用函数的期望。我们假设保险公司的盈余过程近似于具有漂移的布朗运动,金融市场是由一个无风险资产和一个风险资产组成,其中风险资产的价格服从CEV模型。利用随机控制理论,我们建立了HJB方程,并得到了最优策略和最优值函数的表达式。
2. 模型介绍
让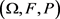 是满足通常条件的完备概率空间,
表示概率空间到时刻t的域流,其中
为给定的正的有限投资时间;
代表到时间t的可用信息。下面介绍的所有随机过程都是这个空间中的适应过程。
是满足通常条件的完备概率空间,
表示概率空间到时刻t的域流,其中
为给定的正的有限投资时间;
代表到时间t的可用信息。下面介绍的所有随机过程都是这个空间中的适应过程。
保险公司的盈余过程描述为C-L模型
其中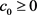 为初始余额;c为保费率;
代表时间t之前的总索赔额,
为具有强度
的齐次泊松过程,并且
是一列正的独立同分布的随机变量,且分布函数为
;索赔的一阶矩和二阶矩分别为
和
。在这里,对于
,
,
,并且对于
,
,其中
为最大索赔额。假设保费收入率c用期望值原则来计算,即,
,其中
为保险公司的安全负荷。
为初始余额;c为保费率;
代表时间t之前的总索赔额,
为具有强度
的齐次泊松过程,并且
是一列正的独立同分布的随机变量,且分布函数为
;索赔的一阶矩和二阶矩分别为
和
。在这里,对于
,
,
,并且对于
,
,其中
为最大索赔额。假设保费收入率c用期望值原则来计算,即,
,其中
为保险公司的安全负荷。
保险公司可以通过购买超额损失再保险来减少索赔带来的风险。让a是保险者的超额损失自留水平, 是保险公司自留的索赔额。经过再保险之后,保险公司的盈余过程变为
其中保费收入率为
为再保险公司的安全负荷,并且 。为了方便,盈余过程 可近似为扩散模型
这里 是一维的标准布朗运动,并且
其中 。
。
假设保险公司可以将财富投资到包含无风险资产和风险资产的金融市场中。无风险资产价格过程满足
其中 是无风险资产的利率。风险资产的价格过程满足CEV模型
其中
是风险资产的预期收益率;
是正的常数;
是弹性系数并且假设
;
是瞬时波动率;
是一维的标准布朗运动,且 与相互独立。
与相互独立。
表示t时刻保险公司的财富, 表示t时刻的超额损失自留水平, 表示投资到风险资产中的数额。 表示一个交易策略。在策略 下,财富过程 表示为
(1)
并且具有初始条件 。
3. 效用函数下的鲁棒问题
假设保险公司具有指数效用函数
(2)
其中 为保险公司的绝对风险厌恶系数。传统上,假设保险公司的模糊-中性目标函数为
(30
然而,在本文中,我们将模型不确定性考虑到最优投资和再保险问题中。由于考虑到模型的模糊性,保险公司使用模型(1)作为它的参考模型,保险公司并不完全信任参考模型,它可以考虑一个替代模型来获得稳健的最优策略。我们采用概率测度Q来表示备选模型,且Q与P是等价的。 定义为概率测度集,即, 。
定义过程
使得
,其中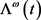 有下面的形式
有下面的形式
(4)
根据Girsanov’s定理,在备选测度Q下,上面提到的布朗运动可写为
(5)
CEV模型描述为
 (6)
(6)
并且财富过程描述为
(7)
定义1:
交易策略 定义为可行策略,如果它满足如下条件:
1) 是可测的;
2) , , ;
3) ,SDE (7)有唯一(强)解 且 , 是描述最坏情况下的备选模型。
对任意的初始条件 ,所有的可行策略组成的集合记为 。
我们假设保险公司确定一个稳健投资组合策略,这个策略是在一些最坏情况模型下的最好选择。为了解决问题(3),我们定义值函数为
 (8)
(8)
其中 ,(8)的第二项表示备选测度与参考测度下的偏离, 表示模型不确定性的偏好系数。我们用相对熵来描述参考测度P和备选测度Q之间的偏差,相对熵从t到 的增量为
为了方便,我们根据参考文献Maenhout [11] 假设 是非负状态相依的,并且有下面的形式
(9)
其中 是关于扩散风险的模糊厌恶系数。
根据动态规划原理,由Maenhout [11] ,鲁棒HJB方程可描述为
(10)
并且具有边界条件 , 是无穷小生成元有如下形式
(11)
假设
是HJB方程(10)的一个解且满足
和 。根据(2),我们猜想V有下面的形式
。根据(2),我们猜想V有下面的形式
(12)
由边界条件 ,我们有 和 。经过简单计算得到V的偏导数如下
(13)
将(13)代入到方程(10)中,固定点 和a,由一阶条件可求得最小值点
(14)
将(14)代入到(10)且由一阶条件容易得到最大值点
(15)
类似地,我们可得到最大值点 满足
(16)
如果 ,则 且有
(17)
由假设 ,我们得到 。下面我们在两种情形下讨论最优问题:
情形1:如果 ,我们有 。则对于 , 。将(14),(15)和(17)代入(10)中可得
(18)
考虑边界条件 ,我们得到
(19)
其中
对于式子(18),我们猜想其中一个解有如下形式
(20)
并且具有 , 。把(20)代入(18)得到
(21)
考虑边界条件,可得
(22)
情形2:如果 ,我们有 。对于 , ,与情形1类似,有
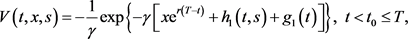
和
 (23)
(23)
(24)
其中 和 会在下面给出。
对于 , 。则 。同时, , 。类似地,我们可以假设方程的解为
并且具有边界条件 和 。则我们得到
(25)
由于 在 点是连续的,则有
我们可以得到
定理1: 是HJB方程(10)的一个解,在CEV模型下具有扩散风险的保险公司的鲁棒最优超额损失再保险和投资策略为
1) 如果 ,
(26)
其中 , 和 由(20),(19)和(22)给出。
2) 如果 ,
(27)
其中 , , 和 由(20),(23),(25)和(22)给出。
定理2:如果存在函数 和控制策略 并且满足HJB方程(10)。则 是一个最优策略且 是相对应的值函数。
证明:由于情形2的证明与情形1是类似的,在这里我们只证明情形1。根据参考文献Kraft [12] 中的推论1.2,若上面的定理成立,则需值函数 和最优策略 满足下面的性质:
(1) 是可行策略;
(2) ;
(3) 。
下面,我们分别验证性质(1)-(3)。
对于性质(1),我们需要验证策略 满足定义1中的条件(1)~(3)。明显地,我们知道定义1中的条件(1)是满足的。定义1中的条件(2)和(3)能够从下面的性质(2)的证明中得到。
对于性质(2)。把 代入(7)中,得
(28)
再把(28)代入(26)中,我们得到
(29)
其中 和 。
由于
,
和
是确定的并且在
上有界,所以(29)中的第一个不等式成立。第二个等式成立是由于
,
,
和 是确定的并且在
上有界。
是确定的并且在
上有界。
下面我们考虑积分 和
,
和
,
(30)
(30)中的第一部分是一个常数,第二部分是鞅。所以 。根据参考文献Zheng等 [10] 中的Lemma 3.6,我们知道 。因此,
(31)
对于性质(3)。把(9)代入性质(3)的式子中,得
(32)
证毕。
4. 总结
在文章中,我们研究了AAI的鲁棒投资和超额损失再保险问题。AAI可以将盈余投资到包含一个无风险资产和一个服从CEV模型的风险资产中。采用动态规划方法,我们得到最优策略和最优值函数的表达式。此外,我们还对该问题的最优再保险和投资策略进行了敏感性分析,得到的结果如下:1) 风险资产的参数对最优再保险策略没有影响;2) 保险业务的参数对最优投资策略没有影响;3) 最优投资策略与股票价格和弹性系数有关。
在未来AAI的鲁棒最优再保险和投资问题的研究中,将我们的分析扩展到更一般的模型是有意义的。此外,我们可以使用其他准则,如均值–方差准则。在这种情况下,计算起来可能会比较复杂。因此,应该考虑更加实际的方法来处理鲁棒最优投资和超额损失再保险问题。
文章引用
李 冰,耿彩霞. CEV模型下鲁棒最优投资和超额损失再保险问题研究
Research on Robust Optimal Investment and Excess-of-Loss Reinsurance under CEV Model[J]. 统计学与应用, 2018, 07(05): 495-504. https://doi.org/10.12677/SA.2018.75058
参考文献
- 1. Browne, S. (1995) Optimal Investment Policies for a Firm with Random Risk Process: Exponential Utility and Minimizing the Probability of Ruin. Mathematics of Operations Research, 20, 937-958. https://doi.org/10.1287/moor.20.4.937
- 2. Yang, H.L. and Zhang, L.H. (2005) Optimal Investment for Insurer with Jump-Diffusion Risk Process. Insurance Mathematics and Economics, 37, 615-634. https://doi.org/10.1016/j.insmatheco.2005.06.009
- 3. Dias, J.C. and Nunes, J.P. (2011) Pricing Real Options under the Constant Elasticity of Variance Diffusion. Journal of Futures Markets, 3, 230-250. https://doi.org/10.1002/fut.20468
- 4. Gu, A.L., Guo, X.P., Li, Z.F. and Zeng, Y. (2012) Optimal Control of Excess-of-Loss Reinsurance and Investment for Insurers under a CEV Model. Insurance Mathematics and Economics, 51, 674-684. https://doi.org/10.1016/j.insmatheco.2012.09.003
- 5. Gu, M.D., Yang, Y.P., Li, S.D. and Zhang, J.Y. (2010) Constant Elasticity of Variance Model for Proportional Reinsurance and Investment Strategies. Insurance Mathematics and Economics, 46, 580-587. https://doi.org/10.1016/j.insmatheco.2010.03.001
- 6. Wang, Y.J., Rong, X.M. and Zhao, H. (2018) Optimal Investment Strat-egies for an Insurer and a Reinsurer with a Jump Diffusion Risk Process under the CEV Model. Journal of Computational and Applied Mathematics, 328, 414-431. https://doi.org/10.1016/j.cam.2017.08.001
- 7. Zhang, X. and Siu, T.K. (2009) Optimal Investment and Reinsurance of an Insurer with Model Uncertainty. Insurance Mathematics and Economics, 45, 81-88. https://doi.org/10.1016/j.insmatheco.2009.04.001
- 8. Branger, N. and Larsen, L.S. (2013) Robust Portfolio Choice with Un-certainty about Jump and Diffusion Risk. Journal of Banking and Finance, 37, 5036-5047. https://doi.org/10.1016/j.jbankfin.2013.08.023
- 9. Wang, P. and Li, Z.F. (2018) Robust Optimal Investment Strategy for an AAM of DC Pension Plans with Stochastic Interest Rate and Stochastic Volatility. Insurance Mathematics and Economics, 80, 67-83. https://doi.org/10.1016/j.insmatheco.2018.03.003
- 10. Zheng, X.X., Zhou, J.M. and Sun, Z.Y. (2016) Robust Optimal Portfolio and Proportional Reinsurance for an Insurer under a CEV Model. Insurance Mathematics and Economics, 67, 77-87. https://doi.org/10.1016/j.insmatheco.2015.12.008
- 11. Maenhout, P.J. (2006) Robust Portfolio Rules and Detection-Error Probabilities for a Mean-Reverting Risk Premium. Journal of Economic Theory, 128, 136-163. https://doi.org/10.1016/j.jet.2005.12.012
- 12. Kraft, H. (2004) Optimal Portfolios with Stochastic Interest Rates and Defaultable Assets. Springer-Verlag, Berlin. https://doi.org/10.1007/978-3-642-17041-6