Statistics and Application
Vol.
12
No.
04
(
2023
), Article ID:
70075
,
10
pages
10.12677/SA.2023.124085
基于F. E. Smith食物有限模型的中国人口数量预测
郑加乐,郑锦楠
广州大学数学与信息科学学院,广东 广州
收稿日期:2023年7月3日;录用日期:2023年7月24日;发布日期:2023年8月3日

摘要
本文提出了一类基于F. E. Smith修正后的食物模型,用于中国人口预测。通过对传统的logistic人口预测模型和Smith模型进行定性研究和定量预测,对比发现,通过选取适当的质量替换率参数,可以使得食物有限模型的预测效果比logistic模型的预测效果更加精准,从而更好地预测中长期的人口数量变化。
关键词
Smith模型,人口预测,食物有限

Chinese Population Size Prediction Based on F. E. Smith’s Food Finite Model
Jiale Zheng, Jinnan Zheng
School of Mathematics and Information Science, Guangzhou University, Guangzhou Guangdong
Received: Jul. 3rd, 2023; accepted: Jul. 24th, 2023; published: Aug. 3rd, 2023

ABSTRACT
In this paper, a modified food model based on F. E. Smith is proposed for population forecasting in China. Through qualitative research and quantitative prediction on the traditional logistic population prediction model and Smith model, it is found that by selecting appropriate quality replacement rate parameters, the prediction effect of the food-limited model can be more accurate than that of the logistic model, so as to better predict the medium and long-term population change.
Keywords:Smith Model, Population Projections, Limited Food

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
自改革开放以后,中国人口总数就一直在增长,而人口是一个地区的基本情况的重要指标。我们既不希望人口增长太快导致冲破环境容纳量,也不希望人口呈现负增长状态或是出现老龄化等问题。因此,人口预测一直是很多研究者的重点研究对象。如果能够较为精准地预测出未来几年甚至几十年、几百年的中国人口数量大致数值或者演变情况,这对于市场调控、社会发展将有一定的指导性。
2. 经典的函数拟合预测
在文章的开始,我们先介绍经典的函数拟合预测,它是不带任何模型、不考虑任何现实的人口增长规律而直接以MATLAB的工具箱进行预测的。当然,它也是最简单的预测法。
2.1. 拟合函数
函数拟合主要是通过已有数据出发,不考虑其背后人口增长规律而直接拟合出函数,之后根据函数本身对以后的年份进行人口预测,可以大致预测出未来的人口数量。本文先把年份设为x自变量,以中国人口数量设为y因变量,通过《中国统计年鉴》获取到1982~2015年中国总人口数量,运用MATLAB中的cftool工具箱进行多个函数的拟合,如下:
1) 指数函数预测

Figure 1. Exponential function fitting prediction
图1. 指数函数拟合预测
指数函数拟合的R方为0.9563,可见拟合效果不错。然而,按照实际情况来说,食物、环境等资源是有限的,因此不可能总是按指数函数的递增规律发展下去(见图1,展现了指数函数拟合预测效果)。
2) 傅里叶函数预测
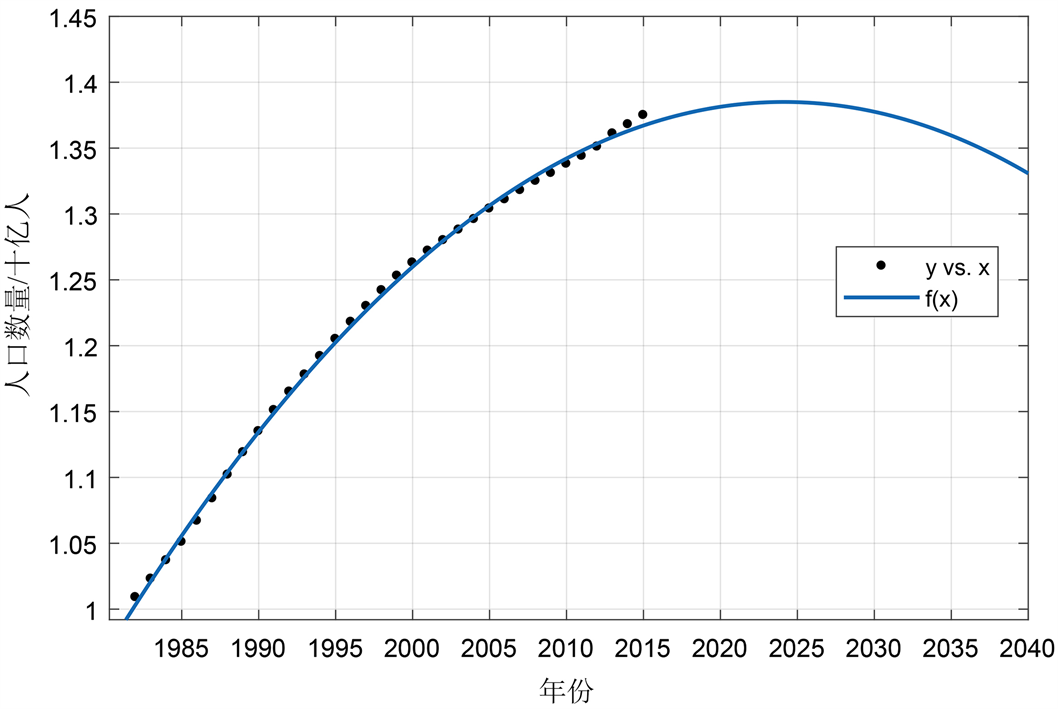
Figure 2. Fourier function fitting prediction
图2. 傅里叶函数拟合预测
傅里叶函数预测的R方为0.999,拟合效果极佳。可以看到,拟合出来的函数曲线,在2025年之前,在保证人口数量增长的前提下,增长速率逐渐趋于平缓,这比较符合人口增长的期望。但在2025年以后,却显示出人口数量直接单调下降的情况,这不符合显示情形。因而,可以说傅里叶函数的短期预测效果好,但中长期预测效果不好(见图2,展现了傅里叶函数拟合预测效果)。
3) 多项式函数预测
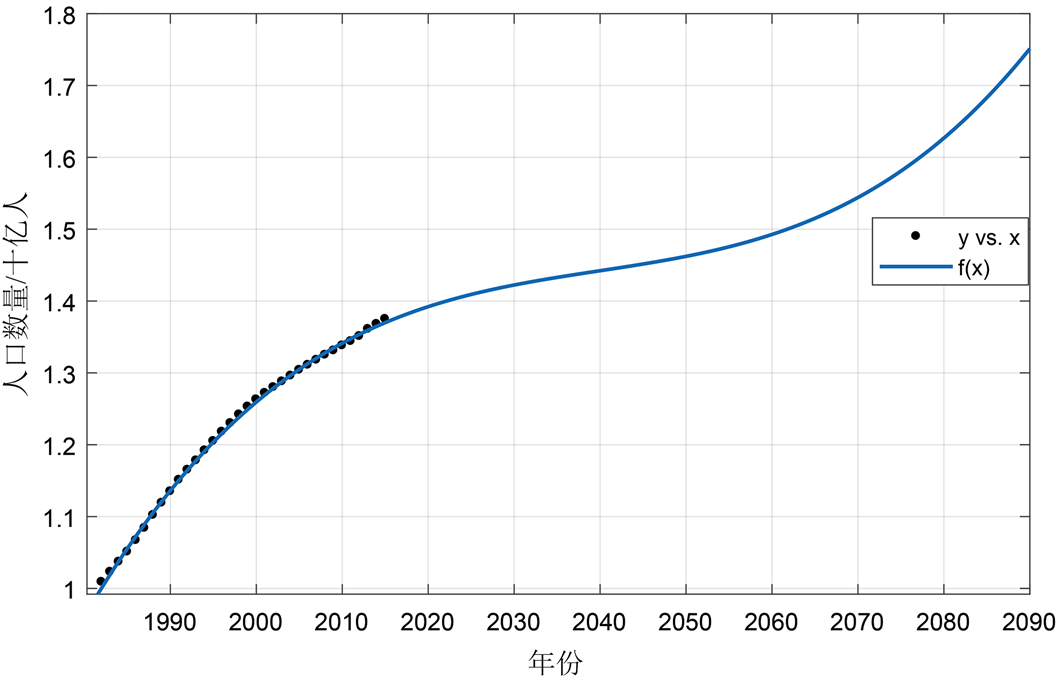
Figure 3. Fitting prediction of cubic polynomial function
图3. 三次多项式函数拟合预测
多项式函数形式较为简单,方便用于快速预测。通过探究,我们发现,一次多项式函数预测极为不妥,二次多项式函数预测情况与傅里叶函数预测情况极为相似,而三次多项式函数预测,R方为0.9991,拟合效果非常好(见图3,展现了三次多项式函数的拟合预测效果)。
可见,其函数图像也是可以用来预测短期人口数量,但无法预测长期人口数量,否则在2060年以后,人口不断上升,增长率也变大,这显然不合理。
2.2. 预测结果
通过2.1节的分析,我们最终选取三次多项式函数进行人口数量的短期预测,拟合之后,其函数表达式如下:
其中,
Table 1. Prediction effect of cubic polynomial function
表1. 三次多项式函数预测效果
依照上面的函数,我们可以预测出人口数量并与真实值对比(见表1)。
3. Logistic人口预测模型
第一部分中的函数拟合由于只考虑人口数据本身,而没有考虑到人口增长过程中的种群增长规则,诸如内禀增长率、环境容纳量等,所以预测效果欠妥,只能预测短期而不能预测长期。事实上,人口的增长大体上是服从一定的方程规律的,尤其是常微分方程经常被用来预测人口数量,如刘 [1] 、宋 [2] 、唐 [3] 、欧阳 [4] 和张 [5] 等人就用了常微分方程模型去预测了人口数量。在本文中,我们先介绍logistic人口预测常微分方程模型——一个多次被运用和修改于人口预测的模型。
3.1. 模型建立
为了预测长期的人口数量的变化,我们需要寻找人口增长的内在规律。如沈 [6] 等人的文章中提到Malthus的人口增长模型,设人口数量为 ,则t时刻人口的增长率为 ,则在假设中国没有环境容纳量的情况下, 应与 成正比,设该比例系数为r,谓之为内禀增长率,即出生率减去死亡率。据此,依文献 [6] 可以建立以下Malthus模型来预测人口数量(其中, 为初始值):
(1)
但鉴于Malthus模型没有考虑当地的最大环境容纳量,实现了无止尽的指数型递增的情形,现实中环境容纳量总是存在的,是不可能出现无止尽的暴增的情况的。基于上述分析,我们假设迁入迁出对中国人口影响忽略不计,中国的环境容纳量固定为K,则在Malthus模型的基础上,可以建立以下Logistic人口增长模型,如文献 [7] 也对此进行了应用。该模型不再呈现指数递增趋势,会有更好的预测效果。
(2)
3.2. 定性研究
根据常微分方程定性理论的相关知识 [8] ,模型(2)的平衡点为 , 。设 ,则:
.
在某一点 处可展开为:
显而易见地 , , , 。那么 在 的泰勒展开为: , 在 的泰勒展开为: 。则: 为不稳定平衡点, 为稳定
平衡点。这意味着,当 , 。即当 , ;当 , 。下面,我们画出方程(2)的相平面图,诸如,我们假定 , (十亿),则方程(2)的相平面如下。

Figure 4. Logistic model phase plane
图4. Logistic模型相平面
由上图4,我们回到人口数量的讨论上,这意味着,我们在中国这个区域中,有一定的环境容纳量,这个环境容纳量被预计在1.6 (单位为十亿)左右。即当人口到达1.6 (单位为十亿),中国的人口将由于环境容纳量的原因,无法再承载更多的人,如果人口超过1.6 (单位为十亿),将会有人吃不饱、穿不暖,导致死亡率上升,最终慢慢的人口会降低回到1.6 (单位为十亿)。反之,当人口低于1.6 (单位为十亿),则环境允许人口继续增长。则上图中的蓝色线的变化趋势,反映出人口增长率下降但人口依旧增长,这非常符合中国人口数量变化。
3.3. 定量预测
3.2中给出了在logistic模型下中国人口变化的定性情况,可以帮助我们掌握模型的定性规律,但它却没有给出定量的变化情况,这里通过求解logistic常微分方程的解,得到:
选取K = 1.6 (十亿), , (十亿),即为2015年人口总数。则有:
通过MATLAB数值模拟,最终得到2016~2050年的人口数量的图像如图5:
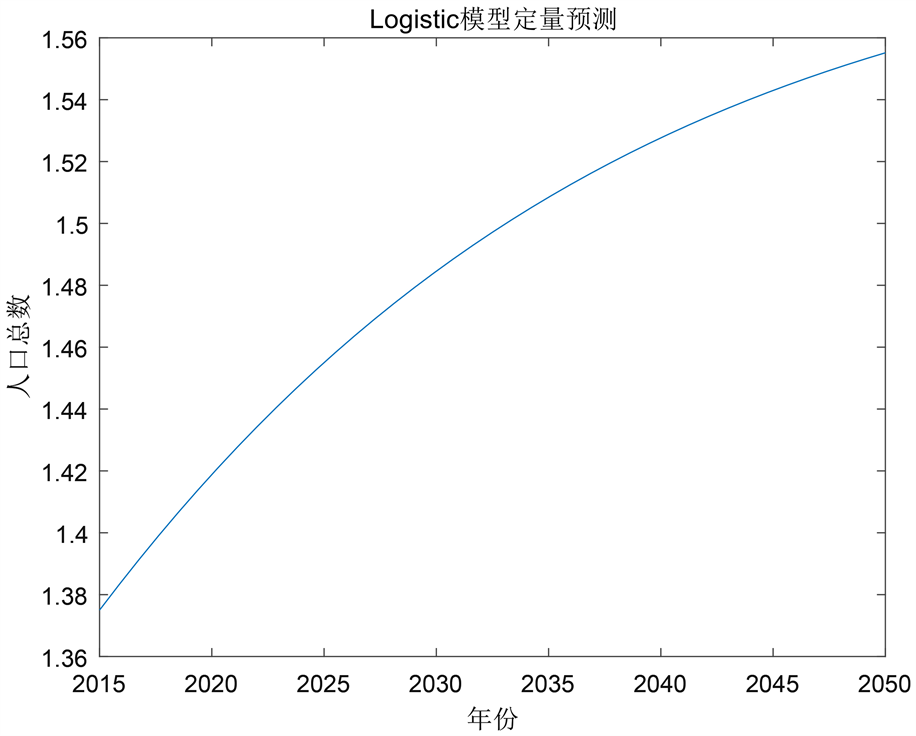
Figure 5. Logistic model quantitative prediction diagram
图5. Logistic模型定量预测图
4. Smith修正的食物有限模型
4.1. 模型建立
对于现在的中国来说,虽然短期内大概率不会发生大面积的食物匮乏的情况,但应该说食物总量也是有限的,尤其是当人口一直增长下去,又或者当发生自然灾难或者人为战争,就有可能导致食物匮乏现象。在食物有限的情况下,F. E. Smith研究了食物有限的情况下水蚤的生长情况,见文章 [9] ,他发现
了 不满足logistic线性关系 ,于是通过研究与实验检测,他提出了如下的食物有限模型:
(3)
其中,c为种群中每单位质量每单位时间的质量替换率,显然地,当 时,方程(3)变为方程(2)。其他参数与方程(2)的意义一致。对于Smith模型,我们发现有许多国内外著名学者也关注到了该模型,如外文文献 [10] [11] [12] 等。在本文中,我们基于食物有限的事实,研究在此情况下的人口增长情况。
4.2. 定性研究
再次根据常微分方程定性理论的相关知识 [8] ,模型(3)的平衡点为 , 。设 ,则:
由泰勒展开理论, 在某一点 处可展开为:
显而易见地,我们有:
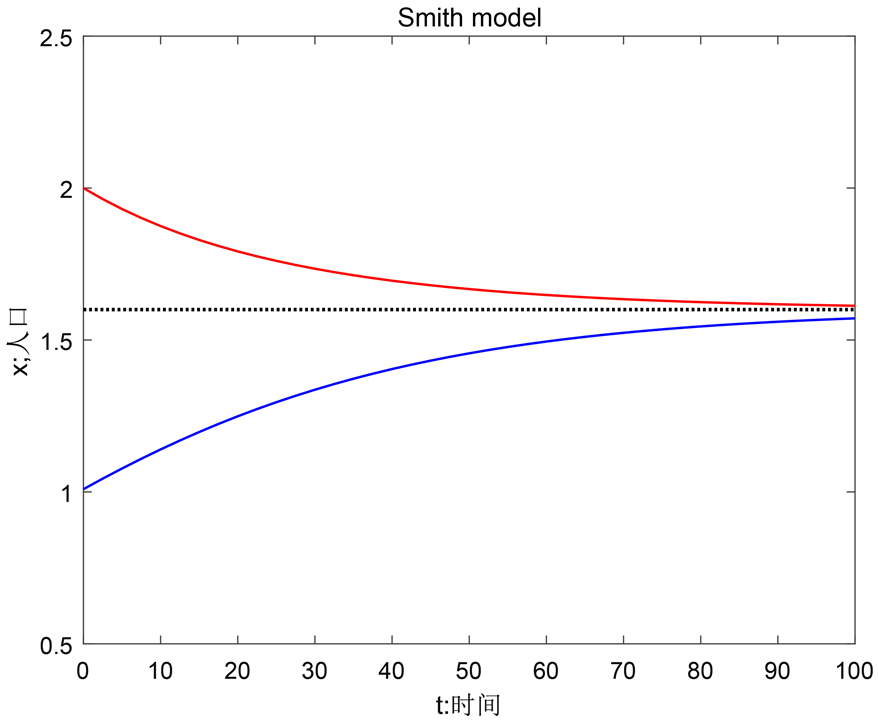
Figure 6. Smith model phase plane
图6. Smith模型相平面
则: 为不稳定平衡点, 为稳定平衡点。这意味着,当 , 。即当 ,
;当 , 。下面,利用MATLAB画出方程(3)的相平面图,仿照(2)的数值模拟情况,我们假定 , (十亿), ,则方程(3)的相平面如图6。
4.3. 定量预测
同样地,为了得到精准的人口数量预测效果,我们设 , (十亿), ,通过MATLAB数值模拟,最终得到2016~2050年的人口数量的图像如图7。
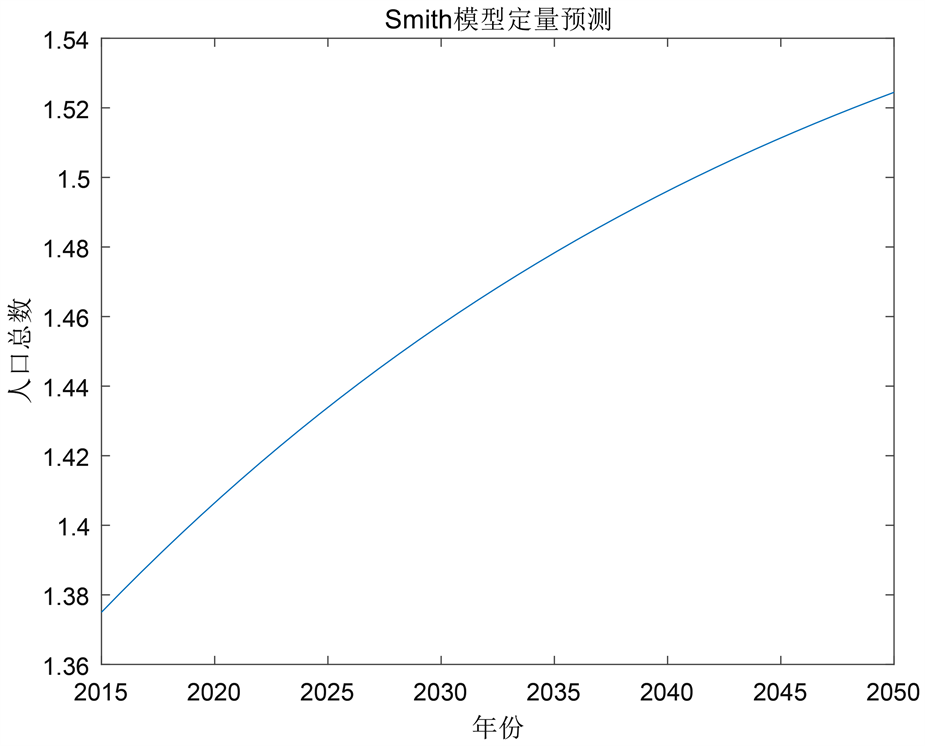
Figure 7. Quantitative prediction diagram of Smith model
图7. Smith模型定量预测图
4.4. 对比讨论
通过对2016~2022年两模型的预测效果和真实人口进行对比,如下表2,我们得到Ligistic模型和Smith模型在2016~2022年对人口的预测值。将这些数据与真实值作差,得到表3。显而易见地,我们发现当选择适当的质量替换率参数之后,Smith模型对比Logistic模型的确会有更好的预测效果,它更加贴近真实值了。
Table 2. Comparison of population predicted values between logistic model and Smith model (unit: billion)
表2. Logistic模型与Smith模型人口预测值对比(单位:十亿)
Table 3. Difference between the predicted population and the true value of the logistic model and the Smith model for each year (unit: billion)
表3. 各年份logistic模型与Smith模型预测人口与真实值差值(单位:十亿)
5. 总结与展望
本文主要研究了logistic及其食物有限修正模型——Smith模型在中国人口预测中的应用,并得到了这两种模型下2016~2050年中国人口数量预测效果。从理论上分析知道,经典的函数预测在短期预测效果极佳,但对于长期预测来说就不准确了,因人口增长是服从生物规律的,不能仅仅只从先前的数据来拟合出函数去预测长期人口变化。而具有实际意义的logistic模型用来预测长期人口变化则比经典的函数预测要更让人信服,另一方面,具有Smith模型的预测是在logistic模型的基础上增加了食物有限的情况,该模型从理论上来说会比logistic更加符合现实情况,也会预测得更加准确,尤其是在发生自然灾害和战争等因素而导致食物匮乏之后。
食物有限的情况在现实生活中是绝对存在的,本文提出的Smith模型较之logistic模型有更好的预测中国人口数量变化的效果。当然,在现实世界中,还有很多因素干扰着人口的变化,诸如新冠疫情等突发病情,再如“时间滞后”等现实因素,因此,人口预测模型依然是个值得挖掘的问题,未来也将会有源源不断的更加贴近现实的预测模型产生。
文章引用
郑加乐,郑锦楠. 基于F. E. Smith食物有限模型的中国人口数量预测
Chinese Population Size Prediction Based on F. E. Smith’s Food Finite Model[J]. 统计学与应用, 2023, 12(04): 814-823. https://doi.org/10.12677/SA.2023.124085
参考文献
- 1. 刘庆山, 胡学平, 来江涛. 基于修正人口发展方程对安徽省人口的预测分析[J]. 高师理科学刊, 2022, 42(1): 1-6.
- 2. 宋晓敏, 周海燕, 王静, 卢秋月. 微分方程在成都市人口预测中的应用[J]. 内江科技, 2022, 43(1): 59-61.
- 3. 唐贤芳, 刘小刚, 张如. 微分方程在西安市人口预测中的应用[J]. 西安文理学院学报(自然科学版), 2017, 20(2): 15-19.
- 4. 欧阳瑞, 张丽娟. 基于常微分方程的周口市人口增长预测[J]. 周口师范学院学报, 2014(5): 25-27.
https://doi.org/10.13450/j.cnki.jzknu.2014.05.008 - 5. 张红芹. 微分方程在人口预测中应用[J]. 吉林省教育学院学报(学科版), 2011, 27(10): 60-61.
- 6. 沈小凤, 蔡果兰, 刘晓娜. Malthus模型在民族地区人口预测中的有效性分析——以青海省民族自治州为例[J]. 硅谷, 2011(10): 121-122.
- 7. 熊波. 人口增长的Logistic模型分析及其应用[J]. 商业时代, 2008(27): 6-7.
- 8. 马知恩. 常微分方程定性与稳定性方法[M]. 北京: 科学出版社, 2015: 6.
- 9. Smith, F.E. (1963) Population Dynamics in Daphnia Magna and a New Model for Population Growth. Ecology, 44, 651-663.
https://doi.org/10.2307/1933011 - 10. Hallam, T.G. and Deluna, J.T. (1984) Effects of Toxicants on Populations: A Qualitative Approach III. Journal of Theoretical Biology, 109, 411-429.
https://doi.org/10.1016/S0022-5193(84)80090-9 - 11. Gopalsamy, K., Kulenovic, M.R.S. and Ladas, G. (1990) Environmental Periodicity and Time Delays in a “Food-Limited” Population Model. Journal of Mathematical Analysis and Applications, 147, 545-555.
https://doi.org/10.1016/0022-247X(90)90369-Q - 12. Hallam, T.G. and Deluna, J.T. (1984) Effects of Toxicants on Populations: A Qualitative: Approach III. Environmental and Food Chain Pathways. Journal of Theoretical Biology, 109, 411-429.
https://doi.org/10.1016/S0022-5193(84)80090-9
