Advances in Applied Mathematics
Vol.04 No.03(2015), Article ID:15826,8
pages
10.12677/AAM.2015.43029
Generalized Inverse Eigenvalue Problem and Model Updating for Discrete Beam
Zhenwei Sun, Ruru Ma, Zhigang Jia
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou Jiangsu
Email: sunzhenwei1990@163.com, maruru7271@126.com, jiazhigang1980@126.com
Received: Jul. 16th, 2015; accepted: Aug. 3rd, 2015; published: Aug. 10th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we study the generalized inverse eigenvalue problem and the optimal model updating problem according to two given eigenpairs, while the total mass of beam is unknown. We present the general solution of the inverse generalized eigenvalue problem. Aiming at the beam model updating problem, we use the least squares method to compute the optimal quality parameter to minimize the distance between the physical parameters of the new beam system and those of the original one.
Keywords:Generalized Inverse Eigenvalue Problem, Least Squares, Matrix Norm, Model Updating, Optimal Solution
梁的广义特征值反问题及离散模型修正
孙振威,马茹茹,贾志刚
江苏师范大学数学与统计学院,江苏 徐州
Email: sunzhenwei1990@163.com, maruru7271@126.com, jiazhigang1980@126.com
收稿日期:2015年7月16日;录用日期:2015年8月3日;发布日期:2015年8月10日

摘 要
本文研究当梁的总质量未知时给定两个特征对的广义特征值反问题与梁的最佳模型修正问题,给出了广义特征值反问题的通解表达式。针对梁的模型修正问题,利用最小二乘方法选取最优参数,使得新梁的物理参数与原梁物理参数的误差达到最小。
关键词 :广义特征值反问题,最小二乘,矩阵范数,模型修正,最优解

1. 引言
在科学与工程计算问题中,梁是一种不可或缺的工程构件,其离散形式为弹簧–质点–刚杆模型[1] 。梁的广义特征值反问题是指由频率(广义特征值)和对应的模态(广义特征向量)来确定梁的各项物理参数,比如梁的横截面积、弹性模量、惯性矩、密度等参数[1] -[3] 。Ram [4] 在给定步长的条件下,利用一个特征值和两个特征向量来构造梁的有限差分模型的质量和刚度;田和戴[5] 利用两个特征对及总质量构造离散梁的刚度及质量,并给出问题有唯一解的充要条件。本文将研究离散梁的广义特征值反问题,利用梁的两个广义特征对构造离散梁的系统参数,即质量和刚度;并且进一步研究如何根据任意给定的两个广义特征对选取最佳总质量使得构造的新系统逼近原系统,即使得模型的修正量达到最小。
横向自由振动梁的偏微分方程模型[1] -[3] 为:

其中 表示梁的横截面积,
表示梁的横截面积, 是梁的弹性模量,
是梁的弹性模量, 是梁的密度,
是梁的密度, 是梁关于中性轴的二次惯性矩,常数L表示梁的长度。在梁的一端固定而另一端自由振动的条件下,求解上述微分方程等价于求解广义特征值问题
是梁关于中性轴的二次惯性矩,常数L表示梁的长度。在梁的一端固定而另一端自由振动的条件下,求解上述微分方程等价于求解广义特征值问题
 (1)
(1)
其中 是广义特征值,
是广义特征值, 为对角线元素大于零的质量矩阵,
为对角线元素大于零的质量矩阵, ,
, ,K为对称五对角刚度矩阵,
,K为对称五对角刚度矩阵,

 ,
, ,
,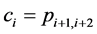 ,
, ,
, ,
, 并且
并且 (
( ),步长
),步长 ,梁的总长度为
,梁的总长度为 。
。
令

则广义特征值问题即公式(1)可变化标准特征值问题
 (2)
(2)
梁的广义特征值反问题与最佳模型修正问题的数学描述如下:
问题1 (广义特征值问题):构造具有两个给定的广义特征对 和
和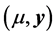 的悬臂梁系统
的悬臂梁系统 。
。
问题2 (模型修正问题):设原梁的系统参数为 和
和 ,记
,记 ,
, ,
,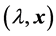 和
和 为两个给定的广义特征对。在问题1有解的条件下选取最佳的悬臂梁系统
为两个给定的广义特征对。在问题1有解的条件下选取最佳的悬臂梁系统 ,使得
,使得 达到最小值。
达到最小值。
文献[5] 中的问题BIMP要求系统的总质量是确定的,而在本文的问题1中并没有限制系统的总质量。与文献 [5] 给出问题BIMP存在唯一解的充要条件类似,我们将给出问题1有解的充要条件和带参数的通解表达式。进一步,问题2描述了如何在问题1的通解中构造与原系统参数相比修正量最小的新系统。
2. 广义特征值问题和模型修正问题
问题1是一类特殊的广义特征值反问题,我们首先给出其有解的充要条件和含参数的通解表达式。然后在该问题有解的条件下,利用最小二乘算法求解问题2的最佳逼近解。
在给出问题1有解判别定理之前,我们需要引入如下记号、定义和引理。不失一般性,按照等步长情形来讨论(类似可以讨论非等步长的情形)。设两个给定的广义特征对为 和
和 ,其中
,其中 ,
, 。令
。令 。定义如下记号
。定义如下记号


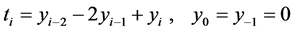






2.1. 广义特征值问题
定义1 [1] :如果一个矩阵非奇异,完全非负的且具有正的拟对角元,则该矩阵为振荡矩阵。
定义2 [1] :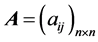 的符号逆转矩阵
的符号逆转矩阵 是指其元素具有关系:
是指其元素具有关系: 。
。
定义3 [1] :如果一个矩阵的符号逆转矩阵为振荡矩阵,则称该矩阵为符号振荡矩阵。
引理1 [2] :梁的离散模型的刚度矩阵K以及矩阵B都是符号振荡矩阵。
引理2 [3] :符号振荡矩阵的特征值为互异的正实数。
下面给出问题1的有解判别定理。
定理1:问题1有解的充要条件是:
(1)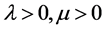 ;
;
(2) 的相邻的两个分量不同时为零,若某个
的相邻的两个分量不同时为零,若某个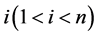 使得
使得 或者
或者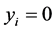 ,则
,则 或者
或者 ;
;
(3)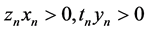 ,
, ;
;
(4) ,且
,且 同号
同号 。
。
证明:先证明必要性。假设已经存在质量参数和刚度参数 和
和 使得一个离散的系统具有两个特征对
使得一个离散的系统具有两个特征对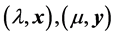 。下面证明特征对
。下面证明特征对 满足定理中的四个条件。
满足定理中的四个条件。
由定义1,定义2和引理1知,k是符号振荡矩阵和M是正定矩阵。在标准特征值问题即公式(2)中,矩阵B也是符号振荡矩阵。根据引理2,B的特征值皆为正实数,即有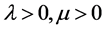 ,条件(1)得证;根据文献[6] 可知条件(2)成立;下证条件(3)与(4)。
,条件(1)得证;根据文献[6] 可知条件(2)成立;下证条件(3)与(4)。
由于 都是广义特征值问题的解,则有
都是广义特征值问题的解,则有
 (3)
(3)
根据上述定义的记号,从公式(3)的第 个分量可得
个分量可得


将上式中的 等各个参数的表达式带入上式并整理得
等各个参数的表达式带入上式并整理得
 ,
,
 ,
,
上式记成矩阵的符号,即
 (4)
(4)
其中 。
。
从公式(4)的第 个分量可以得到
个分量可以得到
 (5)
(5)
由于 是系统的参数,故有
是系统的参数,故有 ,再将公式(5)中的两式相比可得
,再将公式(5)中的两式相比可得

即条件(3)得证。
由公式(4)的第 个分量并结合公式(5)可得
个分量并结合公式(5)可得
 (6)
(6)
将公式(6)式看作关于未知数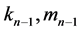 的一个方程组,消元,可得
的一个方程组,消元,可得
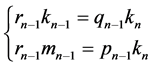 (7)
(7)
因为 是由
是由 确定的,所以
确定的,所以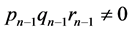 且
且 同号。根据同样的方法讨论当
同号。根据同样的方法讨论当 的时候,将公式(4)的第
的时候,将公式(4)的第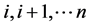 个分量相加在一起,得
个分量相加在一起,得
 (8)
(8)
于是
 (9)
(9)
由于 是系统参数,故
是系统参数,故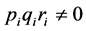 且
且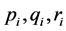 同号即条件(4)得证。
同号即条件(4)得证。
下证充分性。假设特征对 符合定理中的(1)、(2)、(3)、(4)条件,根据公式(5),不妨令
符合定理中的(1)、(2)、(3)、(4)条件,根据公式(5),不妨令
 (10)
(10)
同时取 ,那么必有
,那么必有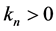 ,根据必要性的证明可知,
,根据必要性的证明可知,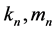 必然符合公式(5)。
必然符合公式(5)。
另外当 时,令
时,令
 (11)
(11)
可以验证 同时符合公式(6)和(8),因此
同时符合公式(6)和(8),因此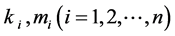 满足公式(4)。下求
满足公式(4)。下求 ,由于总质量
,由于总质量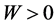 ,即
,即
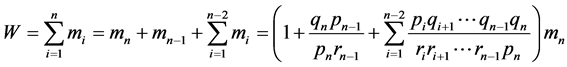 (12)
(12)
故
 (13)
(13)
综上,如果给定的两个特征对 满足定理中的条件(1)~(4),即可构造一组新的与悬臂梁的总质量有关的系统,即问题1有解且通解的表达式为(10),(11)和(13)。
满足定理中的条件(1)~(4),即可构造一组新的与悬臂梁的总质量有关的系统,即问题1有解且通解的表达式为(10),(11)和(13)。
在定理1的证明中,我们给出问题1的通解表达式,其中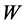 为质量参数,下给出问题1的算法。
为质量参数,下给出问题1的算法。
算法1:已知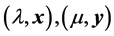 求问题1中新系统的参数
求问题1中新系统的参数 。
。
(1) 由给定的系统物理参数 生成质量矩阵
生成质量矩阵 ,刚度矩阵
,刚度矩阵 及
及 ;
;
(2) 用 计算原系统的特征值与特征向量,任意取出两个特征对
计算原系统的特征值与特征向量,任意取出两个特征对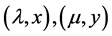 计算
计算 ,
, ;
;
(3) 如果 ,
,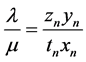 ,
, ,且
,且 同号
同号 ;则由上述公式(10),(11)和(13)计算新的系统参数
;则由上述公式(10),(11)和(13)计算新的系统参数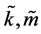 。
。
2.2. 模型修正问题
在问题1的基础上,本节讨论如何选取悬臂梁的总质量 ,使得所求出的参数
,使得所求出的参数 与系统原参数
与系统原参数 误差最小。由于悬臂梁的参数
误差最小。由于悬臂梁的参数 是与总质量
是与总质量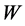 有关的函数,不妨记
有关的函数,不妨记

其中

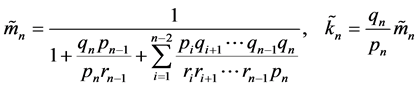
现分析如何选取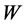 使得
使得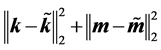 达到最小值。
达到最小值。
问题2等价于求解如下最小二乘问题:

其中

下面利用正交化算法求解该最小二乘问题。
设 ,根据
,根据 分解定理[7] 知
分解定理[7] 知 有如下分解:
有如下分解:
 ,
,
其中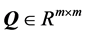 是正交矩阵,
是正交矩阵, 是具有非负对角元的上三角阵。将
是具有非负对角元的上三角阵。将 分块
分块
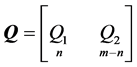 ,
,
并且令

则有
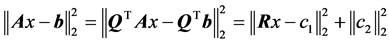 ,
,
于是 是
是 的解当且仅当
的解当且仅当 是
是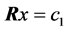 的解。于是最小二乘问题的解可以通过求解上三角矩阵方程组
的解。于是最小二乘问题的解可以通过求解上三角矩阵方程组 得到。
得到。
综合以上讨论,可得到正交化求解最小二乘问题的算法:
算法2:输入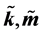 与
与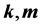 ,
,
(1) 根据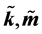 与
与 与计算
与计算 ;
;
(2) 计算 的
的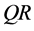 分解;
分解;
(3) 计算 ;
;
(4) 求解方程组 可以得到
可以得到 。
。
3. 数值算例
例1:现有一个悬臂梁,它的总长度为 ,它的单元长度为
,它的单元长度为 ,
, ,
,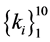 分别表示离散梁的质量与刚度参数:
分别表示离散梁的质量与刚度参数:


(1) 在总质量 未知的条件下,生成新的质量和刚度参数
未知的条件下,生成新的质量和刚度参数 。
。
(2) 选取合适的总质量 使得新系统的物理参数
使得新系统的物理参数 与原物理参数
与原物理参数 的误差最小。
的误差最小。
解:
(1) 根据梁的模型可以得到刚度矩阵和质量矩阵分别为


第7阶频率对应的特征值为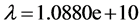 ,对应的模态为
,对应的模态为

第8阶频率对应的特征值为 ,对应的模态为
,对应的模态为

利用这两个特征对构造新的悬臂梁系统.根据算法1,可得

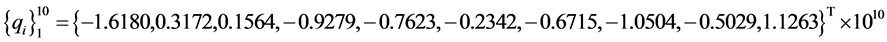

经验证,满足定理1所需条件,可求得系统物理参数为:


该结果与原系统参数完全一致。
(2) 根据算法2,利用最小二乘算法,计算出悬臂梁的总质量为
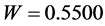
例2:已知某系统的质量与刚度参数为


任取例1中悬臂梁系统的两个广义特征对 与
与 ,其中
,其中

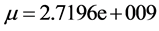


利用这两个特征对去逼近原系统,生成一个新系统的物理参数为

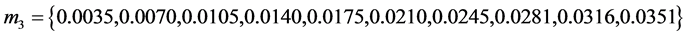
并且求得的最佳总质量为 ,此时新系统与原系统的误差达到最小。
,此时新系统与原系统的误差达到最小。
4. 结论
本文以悬臂梁为背景,给出一类广义特征值反问题有解的充要条件和通解表达式;提出最佳模型修正问题,并利用最小二乘算法求出最佳模型的质量参数。通过算例验证了算法的可行性。所得结论对解决实际工程问题具有一定的指导意义。
致谢
感谢审稿人和编辑的建议与评论。
基金项目
江苏师范大学研究生科研创新项目。
文章引用
孙振威,马茹茹,贾志刚. 梁的广义特征值反问题及离散模型修正
Generalized Inverse Eigenvalue Problem and Model Updating for Discrete Beam[J]. 应用数学进展, 2015, 04(03): 230-237. http://dx.doi.org/10.12677/AAM.2015.43029
参考文献 (References)
- 1. Gladwell, G.M.L. (1986) Inverse Problems in Vibration. Martinus Nijhoff Publishers, Dordrecht, 59-119. http://dx.doi.org/10.1007/978-94-015-1178-0
- 2. Gladwell, G.M.L. (1984) Inverse Problems for the Vibrating Beam. Proceedings of the Royal Society of London A, 393, 277-295. http://dx.doi.org/10.1098/rspa.1984.0058
- 3. Gladwell, G.M.L. (1986) The Inverse Problems for the Eu-ler-Bernoulli Beam. Proceedings of the Royal Society of London A, 407, 199-218. http://dx.doi.org/10.1098/rspa.1986.0093
- 4. Ram, Y.M. (1994) Inverse Mode Problems for the Discrete Model of a Vibrating Beam. Journal of Sound and Vibration, 169, 239-252. http://dx.doi.org/10.1006/jsvi.1994.1016
- 5. 田霞, 戴华 (2005) 梁的离散模型的模态反问题. 振动与冲击, 6, 29-31.
- 6. 戴华 (1994) Jacobi矩阵特征值反问题. 计算物理, 4, 451-456.
- 7. 徐树方, 高立, 张平文 (2013) 数值线性代数. 第二版, 北京大学出版社, 北京, 90-96.