Advances in Applied Mathematics
Vol.05 No.04(2016), Article ID:18925,7
pages
10.12677/AAM.2016.54068
Conditional Uniqueness for an Inverse Source Problem in the Two Dimensional Convection-Diffusion Equations
Qian Liu, Zhendong Wang, Gongsheng Li*
School of Sciences, Shandong University of Technology, Zibo Shandong

Received: Oct. 19th, 2016; accepted: Nov. 7th, 2016; published: Nov. 11th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This article deals with an inverse problem of determining a continuous linear source term in the two dimensional convection-diffusion equation by using the variational adjoint method. A variational identity connecting the known data with the unknown is established based on an adjoint problem, and the conditional uniqueness to the inverse source problem is proved by the approximate controllability to the adjoint problem under the condition that the inverse solution can keep orders locally.
Keywords:Convection-Diffusion Equation, Inverse Source Problem, Adjoint Problem, Variational Identity, Conditional Uniqueness

一个二维对流扩散方程源项反问题的条件 唯一性
刘倩,王桢东,李功胜*
山东理工大学理学院,山东 淄博

收稿日期:2016年10月19日;录用日期:2016年11月7日;发布日期:2016年11月11日

摘 要
本文应用变分伴随方法研究二维对流扩散方程中确定线性连续源项的一个反问题,并基于正问题的伴随问题,建立了一个联系已知数据与未知边界流量的变分恒等式,进而利用对伴随问题的近似控制,在反问题的解满足局部保序性的条件下,证明反问题解的唯一性。
关键词 :对流扩散方程,源项反问题,伴随问题,变分恒等式,条件唯一性

1. 引言
近年来,大气污染及雾霾问题成为社会关注的焦点。对于大气污染物组分构成、积聚过程与运移规律的研究具有重要的科学意义。运用对流扩散模型模拟和分析主要污染物的迁移扩散行为是一种有效的研究方法。对于实际的对流扩散问题,模型中往往有一些未知且不易直接测量得到的物理参数,如扩散的初始分布、扩散系数、以及反映物理/化学规律的源项系数等。这时,利用部分观测数据,形成一个合理的反演问题,则有可能以较小的代价,准确地确定那些未知的模型参数。这是一类抛物型方程的系数反问题 [1] [2] 。
上世纪70年代始,数学物理反问题研究蓬勃发展,基于算子半群理论、Sobolev空间理论与Green函数的不动点方法是研究反问题解的存在唯一性的主要方法。此外,以极值原理、Carleman估计等为理论基础的分析方法也是构建反问题条件适定性的有效方法 [3] [4] [5] [6] [7] 。另一方面,通过引入正问题的伴随问题建立已知数据变化与未知函数改变的变分恒等式,进而探讨反问题的条件适定性的方法逐渐受到关注 [8] - [13] 。这类研究方法不依赖于正问题解的表达式,也不需要进行复杂的估计,而是主要利用变分恒等式与伴随问题的近似可控性理论,被称之为变分伴随方法。文 [14] 对于一般抛物型方程系数反问题的唯一识别问题,介绍了这种研究方法的应用过程。文 [15] 应用这类方法讨论了一维对流弥散方程的源项系数反问题,但其中关于反演解的唯一性证明有纰漏。
本文考虑矩形域上一个二维对流扩散方程的源项反问题。这里的源项反问题是指,当源项具有时空变量分离的线性连续形式时,利用部分边界观测数据确定空间依赖的源项系数。文中将应用变分伴随方法,建立联系已知数据与未知源项系数的变分恒等式,进而利用对伴随问题的近似控制,在反问题的解满足局部保序性的条件下,证明其具有条件唯一性。
2. 正问题与反问题
2.1. 正问题
对于给定的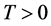 及
及 ,记
,记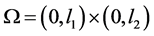 及
及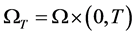 为研究区域,且
为研究区域,且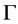 为
为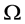 的边界。考虑二维对流扩散方程:
的边界。考虑二维对流扩散方程:
 , (2.1)
, (2.1)
其中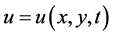 表示污染物的时空浓度,
表示污染物的时空浓度,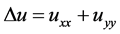 ,
,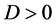 是扩散系数,
是扩散系数,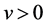 是污染物沿着
是污染物沿着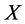 轴方向的对流速度,
轴方向的对流速度,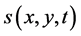 是线性源/汇项。通常情况下,该源项具有变量分离的形式
是线性源/汇项。通常情况下,该源项具有变量分离的形式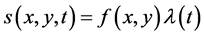 ,其中
,其中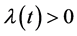 为时间依赖的衰减因子,
为时间依赖的衰减因子,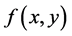 为空间依赖的源强度。
为空间依赖的源强度。
初边值条件给定为
 , (2.2)
, (2.2)
及
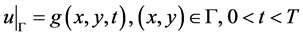 。 (2.3)
。 (2.3)
对于上述初边值问题(2.1)~(2.3),如果所有的模型参数及初边值条件等都是已知的且满足相容性条件,则根据抛物型方程的正则理论,它是一个适定的定解问题,且在 上存在唯一解。这里我们忽略关于正问题(2.1)~(2.3)的有关结论,主要考虑确定空间依赖的源项强度
上存在唯一解。这里我们忽略关于正问题(2.1)~(2.3)的有关结论,主要考虑确定空间依赖的源项强度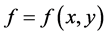 的反问题。
的反问题。
2.2. 反问题
假设区域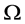 中出现了某种持续性污染现象,且污染物主要由区域内的连续源项产生,而其强度未知。
中出现了某种持续性污染现象,且污染物主要由区域内的连续源项产生,而其强度未知。
不妨设区域的左边界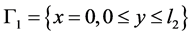 为可观测边界,且可测量通过该边界的污染物流量,即有附加数据:
为可观测边界,且可测量通过该边界的污染物流量,即有附加数据:
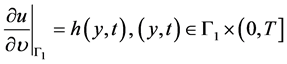 , (2.4)
, (2.4)
其中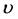 表示边界
表示边界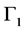 上的单位外法向量,则由(2.4)联合(2.1)-(2.3)形成一个确定源项强度函数
上的单位外法向量,则由(2.4)联合(2.1)-(2.3)形成一个确定源项强度函数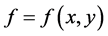 的反问题。
的反问题。
记 。设
。设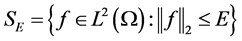 为源项强度函数的容许集,其中
为源项强度函数的容许集,其中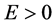 为一个正常数。则对于任意
为一个正常数。则对于任意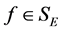 ,正问题有唯一解,记为
,正问题有唯一解,记为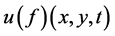 。联系到附加数据条件,定义映射
。联系到附加数据条件,定义映射 :
:
 。(2.5)
。(2.5)
据此,反问题(2.1)~(2.4)可以化为算子方程(2.5)的求解问题。从数值求解的角度,该反问题又可转化为如下带正则化的极小问题
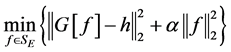 ,(2.6)
,(2.6)
其中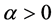 是正则参数。本文主要考虑该反问题解的唯一性问题,数值求解模拟研究结果将另文再表。
是正则参数。本文主要考虑该反问题解的唯一性问题,数值求解模拟研究结果将另文再表。
为此,下述关于齐次热传导方程的边界可控性结论是有用的。
引理1 [16] 设 为有界开区域,其边界
为有界开区域,其边界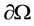 分片光滑。令
分片光滑。令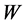 为所有允许的边界函数
为所有允许的边界函数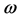 :
: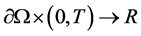 的集合,
的集合,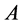 为
为 的任意非空子集。对于
的任意非空子集。对于 ,记
,记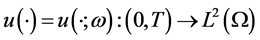 是下述初边值问题的解:
是下述初边值问题的解:
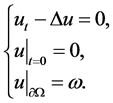 (2.7)
(2.7)
则对于给定的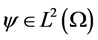 及
及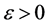 ,存在一个支集在
,存在一个支集在 中的控制函数
中的控制函数 使得
使得
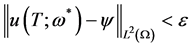 。
。
成立。
引理1的结论对于一般的抛物型方程也是成立的。该引理说明对于一个齐次的线性热传导过程,终值时刻的分布可以由边界值近似控制。
3. 反问题解的唯一性
3.1. 变分恒等式
下面,先建立一个联系已知数据函数和未知函数的变分恒等式。
定理1设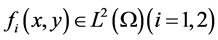 ,且
,且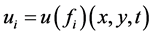 是对应于
是对应于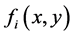 的正问题(2.1)~(2.3)的解,而
的正问题(2.1)~(2.3)的解,而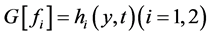 是
是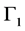 上的流量观测数据,则有变分恒等式
上的流量观测数据,则有变分恒等式
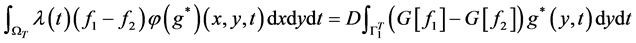 , (3.1)
, (3.1)
其中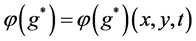 满足下述伴随问题
满足下述伴随问题
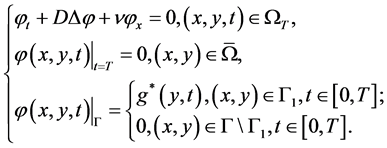 (3.2)
(3.2)
且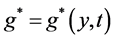 为可控制的边界输入函数。
为可控制的边界输入函数。
证明记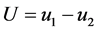 ,则有
,则有
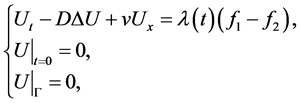 (3.3)
(3.3)
及附加数据
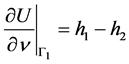 。 (3.4)
。 (3.4)
取试验函数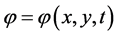 ,分别乘以(3.3)的第一个方程的两边,并在
,分别乘以(3.3)的第一个方程的两边,并在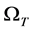 上积分,有
上积分,有
 。
。
对上式左边各项分部积分,利用(3.3)中的零初边值条件,可得
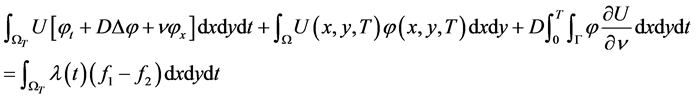 。 (3.5)
。 (3.5)
令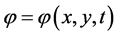 是伴随问题(3.2)的解,则联系到条件(3.4)式,由(3.5)式即得(3.1)式。由于伴随问题(3.2) 的解由边值函数
是伴随问题(3.2)的解,则联系到条件(3.4)式,由(3.5)式即得(3.1)式。由于伴随问题(3.2) 的解由边值函数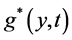 所确定,其解记为
所确定,其解记为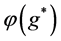 。定理证毕。
。定理证毕。
3.2. 条件唯一性
唯一性是反问题理论研究的重要方面,更是反问题研究中的一个关键问题。对于所考虑的反问题,借助变分恒等式(3.1)及引理1,本节证明若未知的源强度函数在某个小区域内具有严格的保序性,则该反问题的解必是唯一的。这就是所谓的条件唯一性。
定理2 在定理1的条件下,设(A1):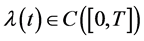 且
且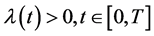 ;(A2):存在
;(A2):存在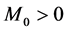 及某个子区域
及某个子区域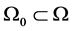 ,使得
,使得 成立,则必有
成立,则必有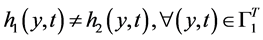 。
。
证明 反证法。假设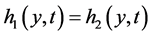 ,
,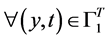 ,即
,即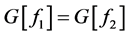 。则由恒等式(3.1)可知
。则由恒等式(3.1)可知
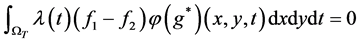 。 (3.6)
。 (3.6)
记
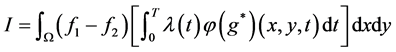 。 (3.7)
。 (3.7)
取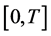 的一个剖分
的一个剖分
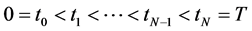 ,
,
并记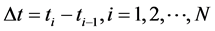 ,则有
,则有
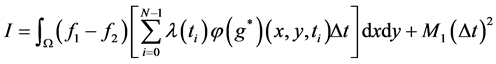 , (3.8)
, (3.8)
其中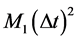 表示截断误差,
表示截断误差, 是正常数。注意到条件
是正常数。注意到条件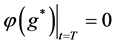 ,这里略去了
,这里略去了 时的项。
时的项。
由定理条件(A2)可知,存在 上的非负可积函数
上的非负可积函数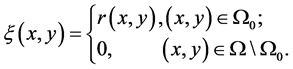 ,其中
,其中 是
是 上的严格非负光滑函数。于是得到
上的严格非负光滑函数。于是得到
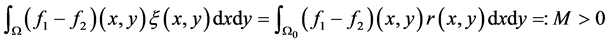 。 (3.9)
。 (3.9)
再由定理条件(A1),可构造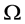 的
的 可积函数序列
可积函数序列
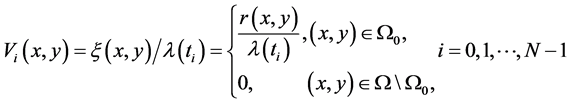 。
。
注意到伴随问题(3.2)是倒向的适定问题,由引理1可知,通过适当选取边界函数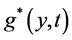 ,伴随问题在
,伴随问题在 时的解
时的解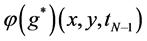 可与目标函数
可与目标函数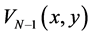 任意接近。以此类推,在每一个子区间
任意接近。以此类推,在每一个子区间 上都有可控的边界输入,使得对任意的
上都有可控的边界输入,使得对任意的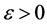 ,有
,有
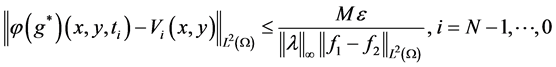 。 (3.10)
。 (3.10)
基于(3.8)式及(3.9)式,利用基本不等式及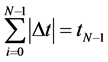 ,可得
,可得
 。 (3.11)
。 (3.11)
注意到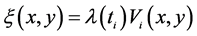 ,对上式右端中间项,利用(3.10)式及Cauthy-Schwartz不等式,成立估计
,对上式右端中间项,利用(3.10)式及Cauthy-Schwartz不等式,成立估计
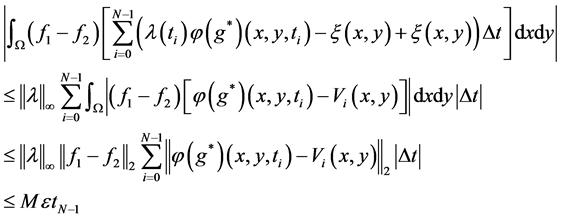 。 (3.12)
。 (3.12)
即有
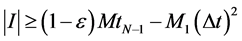 。 (3.13)
。 (3.13)
可知,只要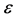 及
及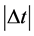 充分小,则必有
充分小,则必有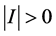 。这与(3.6)式矛盾。定理证毕。
。这与(3.6)式矛盾。定理证毕。
4. 结论
本文对于二维对流扩散方程由部分边界测量数据确定空间依赖源项的反问题,在源函数满足局部保序性的条件下,应用变分伴随方法证明了源项解的唯一性。这种方法的核心是利用伴随问题建立一个联系已知数据与未知函数的变分恒等式,进而通过对伴随问题解的控制进行分析证明。
文中结果对于一般高维有界区域也是成立的,同时也可以应用这种方法建立这类反问题的条件稳定性,这是下一步要考虑的一个主要工作。
基金项目
国家自然科学基金资助项目(Nos. 11371231, 11071148)。
文章引用
刘倩,王桢东,李功胜. 一个二维对流扩散方程源项反问题的条件唯一性
Conditional Uniqueness for an Inverse Source Problem in the Two Dimensional Convection-Diffusion Equations[J]. 应用数学进展, 2016, 05(04): 591-597. http://dx.doi.org/10.12677/AAM.2016.54068
参考文献 (References)
- 1. Isakov, V. (1998) Inverse Problems for Partial Differential Equations. Spring-Verlag, New York. http://dx.doi.org/10.1007/978-1-4899-0030-2
- 2. 李功胜, 姚德. 扩散模型的源项反演及其应用[M]. 北京: 科学出版社, 2014.
- 3. Isakov, V. (1991) Inverse Parabolic Problems with the Final Overdetermination. Communications on Pure and Applied Mathematics, 54, 185-209.
- 4. Yamamoto, M. (1993) Conditional Stability in Determination of Force Terms of Heat Equations in a Rectangle. Mathematical and Computer Modelling, 18, 79-88.
- 5. Isakov, V. (1995) Global Uniqueness for Inverse Parabolic Problems with Final Observation. Inverse Problems, 11, L11-L16. http://dx.doi.org/10.1088/0266-5611/11/4/001
- 6. Isakov, V. (1999) Some Inverse Problems for the Diffusion Equation. Inverse Problems, 15, 3-10. http://dx.doi.org/10.1088/0266-5611/15/1/004
- 7. Choulli, M. and Yamamoto, M. (2004) Conditional Stability in Determining a Heat Source. Journal of Inverse and Ill-Posed Problems, 12, 233-244. http://dx.doi.org/10.1515/1569394042215856
- 8. DuChateau, P. and Rundell, W. (1985) Unicity in an Inverse Problem for an Unknown Term in a Reaction Diffusion Equation. Journal of Differential Equations, 59, 155-164. http://dx.doi.org/10.1016/0022-0396(85)90152-4
- 9. DuChateau, P. (1995) Monotomicity and invertibility of Coefficient to Data Mapping for Parabolic Inverse Problems. SIAM Journal on Mathematical Analysis, 26, 1473-1487. http://dx.doi.org/10.1137/S0036141093259257
- 10. DuChateau, P. (1997) An Inverse Problem for the Hydraulic Properties of Porous Media. SIAM Journal on Mathematical Analysis, 28, 611-632. http://dx.doi.org/10.1137/S0036141095285673
- 11. DuChateau, P., Thelwell, R. and Butters, M. (2004) Analysis of an Adjoint Problem Approach to the Identification of an Unknown Diffusion Coefficient. Inverse Problems, 20, 601-625. http://dx.doi.org/10.1088/0266-5611/20/2/019
- 12. Hasanov, A., DuChateau, P. and Petkas, B. (2006) An Adjoint Problem Approach and Coarsefine Mesh Method for Identification of the Diffusion in a Linear Parabolic Equation. Journal of Inverse and Ill-Posed Problems, 14, 435-463. http://dx.doi.org/10.1515/156939406778247615
- 13. Li, G.S. and Yamamoto, M. (2006) Stability Analysis for Determining a Source Term in a 1-D Advection-Dispersion Equation. Journal of Inverse and Ill-Posed Problems, 14, 147-155.http://dx.doi.org/10.1515/156939406777571067
- 14. DuChateau, P. (2013) An Adjoint Method for Proving Identifiability of Coefficients in Parabolic Equations. Journal of Inverse and Ill-Posed Problems, 21, 639-663. http://dx.doi.org/10.1515/156939406777571067
- 15. 李功胜, 贾现正, 孙春龙, 杜殿虎. 对流弥散方程线性源项系数反演的变分伴随方法[J]. 应用数学学报, 2015, 38(6): 1001-1015.
- 16. McCamy, R.C., Mizel, V.J. and Seidman, T.I. (1968) Approximate Boundary Controllability of the Heat Equation. Journal of Mathematical Analysis and Applications, 23, 699-703. http://dx.doi.org/10.1016/0022-247X(68)90148-0
*通讯作者。