Advances in Applied Mathematics
Vol.06 No.03(2017), Article ID:20587,5
pages
10.12677/AAM.2017.63028
Research on Mutual Application of Advanced Algebra and Mathematical Analysis Theory
Liu Yang, Chengxin Luo
College of Mathematics and System Science, Shenyang Normal University, Shenyang Liaoning

Received: Apr. 28th, 2017; accepted: May 13th, 2017; published: May 22nd, 2017

ABSTRACT
Theory in mathematical analysis is different from that in advanced algebra and related problems in higher algebra. The problems discussed and the methods to solve the problems are different, but there is a close relationship between them. This paper illustrates the mutual penetration and integration of mathematical analysis and related problems in higher algebra by some examples, we present a method to solve algebra problem by functional analysis theory.
Keywords:Symmetric Matrix, Orthogonal Transformation, Compression Mapping Principle, System of Linear Equations
高等代数与数学分析相互渗透溶合应用研究
杨柳,罗成新
沈阳师范大学 数学与系统科学学院,辽宁 沈阳
收稿日期:2017年4月28日;录用日期:2017年5月13日;发布日期:2017年5月22日

摘 要
数学分析与高等代数中的理论及相关问题是不同的,所讨论的问题以及解决方法不尽相同,但二者之间又有着密切的联系。本文通过实例论述数学分析与高等代数有关问题的相互渗透和融合,给出一个用泛函分析方法处理线性代数问题的实例。
关键词 :对称矩阵,正交变换,压缩映射原理,线性方程组

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
数学分析与高等代数是数学专业的两门主干基础课程。从某种意义上说,任何高深的数学方法都是把复杂的数学对象转化为数学分析和高等代数的内容加以研究和处理。虽然这两门课解题方法有些差异,但是有很多密切的联系,在很多方面有内在的渗透与融合。本文的目的是分析高等代数与数学分析一些典型的问题,就其解法上的相互交叉使用及渗透进行探讨,从而提高高等代与数学分析的教学与研究水平,提高综合解题的能力。
2. 预备知识
首先列举数学分析和泛函分析理论中一些重要结论,这些理论在后面讨论中是必要的。
引理1 [1] 椭球体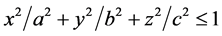 的体积为
的体积为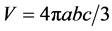 。
。
定义1 [2] 设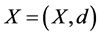 是度量空间,
是度量空间, 是
是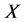 到
到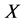 中的映射,如果存在实数
中的映射,如果存在实数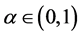 ,使得对所有的
,使得对所有的 ,均有
,均有 ,则称
,则称 是压缩映射。
是压缩映射。
定义2 [2] 设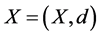 是度量空间,
是度量空间,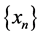 是
是 的点列,如果对任意给定的正数
的点列,如果对任意给定的正数 ,存在正整数
,存在正整数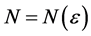 ,使得当
,使得当 时,必有
时,必有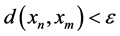 ,则称
,则称 是
是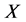 中的柯西列。如果度量空间
中的柯西列。如果度量空间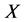 中每个柯西列都在
中每个柯西列都在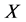 中收敛,那么称
中收敛,那么称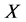 是完备的度量空间。
是完备的度量空间。
引理2 [2] (压缩映射原理)设 是完备的度量空间,
是完备的度量空间,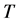 是
是 上的压缩映射,那么
上的压缩映射,那么 有且仅有一个不动点,即存在唯一的
有且仅有一个不动点,即存在唯一的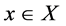 使
使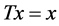 。
。
3. 用高等代数方法解决数学分析问题
本节利用代数方法处理分析问题。
例1设 是实对称正定矩阵,
是实对称正定矩阵,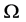 是椭球体:
是椭球体: ,求
,求 的体积。
的体积。
解法一记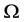 为椭球体
为椭球体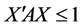 ,其中
,其中 。因为
。因为 是正定矩阵,所以存在正交矩阵
是正定矩阵,所以存在正交矩阵 使得
使得
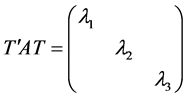
其中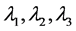 是
是 的特征值,从而均为正数。作正交线性变换
的特征值,从而均为正数。作正交线性变换 ,则
,则
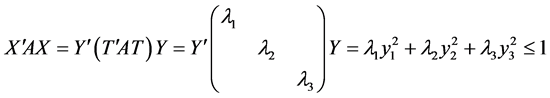
于是体积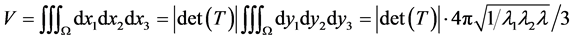 ,
,
其中 为椭球体
为椭球体 。由正交矩阵的性质知
。由正交矩阵的性质知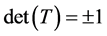 ,所以
,所以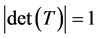 ,而
,而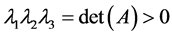 ,所以
,所以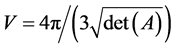 。
。
解法二根据正定矩阵合同于单位矩阵的相关知识,存在可逆矩阵 使
使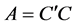 。做另外一种非退化线性替换
。做另外一种非退化线性替换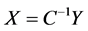 ,这样就把椭球体形状的积分区域变换成了单位球体积分区域,而
,这样就把椭球体形状的积分区域变换成了单位球体积分区域,而
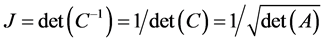 ,从而,
,从而,
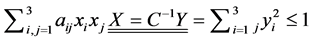
 .
.
例2 [3] 计算三重积分 ,其中
,其中 是不全为0的常数,
是不全为0的常数,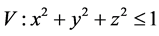 。
。
解将向量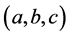 单位化得
单位化得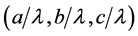 ,其中
,其中 。再将其扩充为三维空间的一个标准正交基:
。再将其扩充为三维空间的一个标准正交基: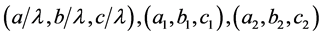 ,作正交变换
,作正交变换
 ,
,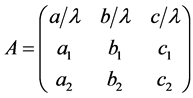 (1)
(1)
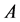 为正交矩阵,
为正交矩阵, ,则
,则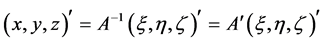 ,两边转置得
,两边转置得
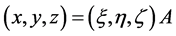 ,
, ,而
,而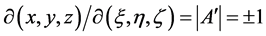 。
。
由(1)得 ,于是由三重积分变量替换公式得
,于是由三重积分变量替换公式得

解完。
由此可见正交变换兼顾了积分区域和被积分函数的特点,比用其它变换来计算更简便。更重要的是此方法具有一般性,它在重积分、广义重积分、曲面积分等中均有应用。
4. 用数学分析方法解决高等代数问题
本节利用分析方法处理代数问题。
例3 设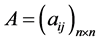 是
是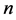 阶实对称矩阵,证明:(1) 若
阶实对称矩阵,证明:(1) 若 ,则
,则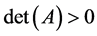 ;(2) 若
;(2) 若 正定,则
正定,则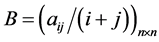 也正定。
也正定。
分析 这是一个纯代数问题,我们用分析方法来证明。数学分析中的一个典型无穷积分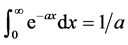 应用于本题中有
应用于本题中有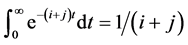 。
。
证明(1) 设 ,已知
,已知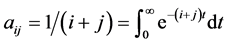 ,则
,则
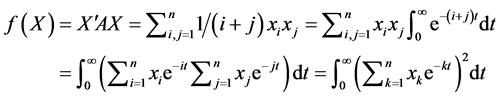
对于一切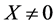 ,被积函数都大于零,所以,积分值大于零,即对于任意
,被积函数都大于零,所以,积分值大于零,即对于任意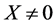 ,都使
,都使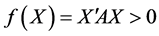 ,因此,
,因此, 是正定二次型,
是正定二次型, 为正定矩阵,所以,
为正定矩阵,所以,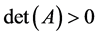 。
。
(2)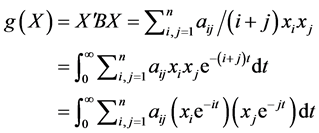
令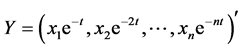 ,则上面的广义积分中被积函数等于
,则上面的广义积分中被积函数等于 。对于任意不为零的向量
。对于任意不为零的向量 亦不为零。而
亦不为零。而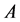 为正定矩阵,故二次型
为正定矩阵,故二次型 正定,即对于任意
正定,即对于任意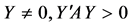 恒成立。综上所述,任意
恒成立。综上所述,任意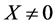 都有
都有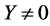 ,则
,则 ,被积函数大于零,积分值一定大于零。所以
,被积函数大于零,积分值一定大于零。所以 为正定二次型,
为正定二次型,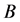 为正定矩阵,证完。
为正定矩阵,证完。
5. 数学分析与高等代数相结合解决问题
本节给出一个用分析方法与代数方法交替使用的实例。
例4设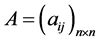 是
是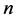 阶实对称矩阵,求二次型
阶实对称矩阵,求二次型
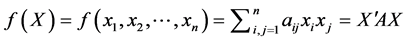
在单位球面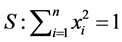 上的最大值、最小值。
上的最大值、最小值。
解(分析法) 函数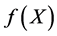 与
与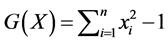 均在
均在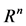 上连续可微,当然
上连续可微,当然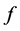 在单位球面
在单位球面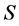 上连续,从而必在此球面(它是有界闭集)某点
上连续,从而必在此球面(它是有界闭集)某点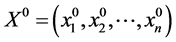 达到最大(小)值。又单位球面无所谓边界点,因此,最大(最小)值点
达到最大(小)值。又单位球面无所谓边界点,因此,最大(最小)值点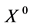 必是稳定点,即有常数
必是稳定点,即有常数 ,使
,使 点满足如下拉格朗日方程
点满足如下拉格朗日方程
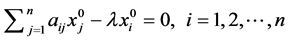
即单位向量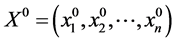 是齐次线性方程组
是齐次线性方程组
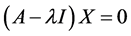 (2)
(2)
的非零解。由(2)知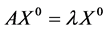 ,因此,
,因此,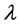 是矩阵
是矩阵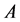 的一个特征值,
的一个特征值,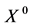 是对应的单位特征向量。在方程组(2)中令
是对应的单位特征向量。在方程组(2)中令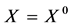 ,再与
,再与 作內积,得
作內积,得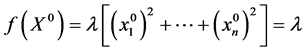 。这表明,
。这表明,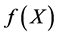 的最大值和最小值都是
的最大值和最小值都是 的特征值。另一方面,设
的特征值。另一方面,设 是实对称矩阵
是实对称矩阵 的任一特征值(它必是实数),与
的任一特征值(它必是实数),与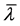 相应的单位特征向量为
相应的单位特征向量为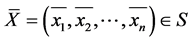 ,则
,则 。
。
再与向量 作内积,便有
作内积,便有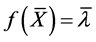 ,这又说明,
,这又说明,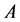 的任一特征值
的任一特征值 等于
等于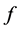 在单位球面某点处的值。解完。
在单位球面某点处的值。解完。
(代数法) 令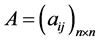 ,
,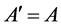 ,设
,设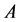 的
的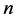 个特征值
个特征值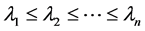 ,
, ,令
,令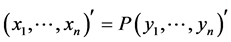 ,即
,即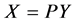 ,其中
,其中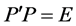 ,
,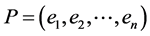 ,
, 是
是 的属于
的属于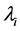 的正交单位向量;
的正交单位向量;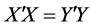 ,则
,则 ,显然
,显然
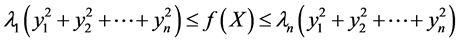 ,
,
可得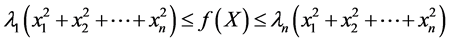 ,即
,即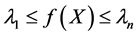 。
。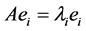 ,
,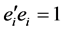 。所以
。所以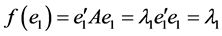 ,
,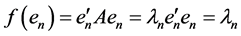 。故
。故 使
使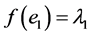 ,
, ,
, 的最大、最小值分别是矩阵
的最大、最小值分别是矩阵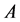 的最大、最小特征值。解完。
的最大、最小特征值。解完。
注 根据上述的推导可知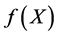 在单位球面上的最大、最小值分别是矩阵
在单位球面上的最大、最小值分别是矩阵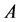 的最大、最小特征值,因此,我们可以通过求对称矩阵
的最大、最小特征值,因此,我们可以通过求对称矩阵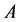 的特征值得到
的特征值得到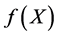 的最大、最小值。反之,也可以通过求
的最大、最小值。反之,也可以通过求 的最大、最小值而得到矩阵
的最大、最小值而得到矩阵 的最大、最小特征值。
的最大、最小特征值。
6. 用泛函分析法处理代数问题
本节用泛函分析法处理线性方程组解的存在唯一性问题。
例5 [4] 考虑线性方程组 ,其中
,其中 ,
,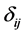 为克罗内克符号,则方程组存在唯一解。
为克罗内克符号,则方程组存在唯一解。
证明将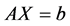 变形为
变形为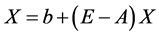 ,构造映射
,构造映射 ,
,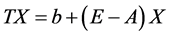 ,
, ,
, ,
,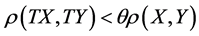 ,
,
其中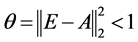 ,从而
,从而 是完备距离空间
是完备距离空间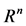 上压缩映射,由引理2,
上压缩映射,由引理2, 有唯一不动点使得
有唯一不动点使得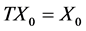 ,即
,即 。证完。 [5]
。证完。 [5]
基金项目
国家自然科学基金(No.11171050);辽宁省教育厅项目(No.L2014433)科研立项。
文章引用
杨柳,罗成新. 高等代数与数学分析相互渗透溶合应用研究
Research on Mutual Application of Advanced Algebra and Mathematical Analysis Theory[J]. 应用数学进展, 2017, 06(03): 238-242. http://dx.doi.org/10.12677/AAM.2017.63028
参考文献 (References)
- 1. 华东师范大学数学系. 数学分析[M]. 第四版. 北京: 高等教育出版社: 2010.
- 2. 王声望, 郑维行. 实变函数与泛函分析基础[M]. 第四版. 北京: 高等教育出版社, 2010.
- 3. 米永生, 米冬梅. 高等代数方法在数学分析中应用[J]. 长春大学学报, 2005, 15(2): 66-69.
- 4. 王宗尧, 薛以峰, 钱张军. 应用泛函分析[M]. 上海: 华东理工大学出版社, 2002: 95-96.
- 5. 王萼芳, 石生明. 高等代数[M]. 第四版. 北京: 高等教育出版社, 2013.