Advances in Applied Mathematics
Vol.07 No.02(2018), Article ID:23753,11
pages
10.12677/AAM.2018.72019
Enhanced Fireworks Algorithm with Adaptive Explosion Amplitude and Differential Variation
Wenwen Ye, Jiechang Wen
School of Applied Mathematics, Guangdong University of Technology, Guangzhou Guangdong

Received: Jan. 18th, 2018; accepted: Feb. 3rd, 2018; published: Feb. 13th, 2018

ABSTRACT
Enhanced fireworks algorithm improves the performance defect of the fireworks algorithm, and shows good effect in many optimization problems. However, it still has low precision and is easy to fall into local optimal solution prematurely in some functions. In order to improve the above mentioned problems, the maximum explosion amplitude is set as the simulated annealing factor to accelerate its search process, and we learn from the idea of differential variation to increase the diversity of the population, so as to jump out of the local optimal solution. The proposed algorithm is tested on 10 benchmark functions and the experimental results show that the proposed algorithm significantly outperforms the enhanced fireworks algorithm and the fireworks algorithm.
Keywords:Enhanced Fireworks Algorithm, Simulated Annealing, Adaptive Explosion Amplitude, Differential Variation
自适应爆炸半径和差分变异的增强烟花算法
叶雯雯,温洁嫦
广东工业大学应用数学学院,广东 广州
收稿日期:2018年1月18日;录用日期:2018年2月3日;发布日期:2018年2月13日

摘 要
增强烟花算法对烟花算法存在的性能缺陷进行改进,并在许多优化问题中显示出不错的效果。然而,增强烟花算法在某些函数上寻优精度低、且容易过早地陷入局部最优解。为了改善这种缺陷,将其最大爆炸半径设置为模拟退火因子来自适应地加速其搜索过程,并借鉴差分变异中的思想以增加种群的多样性,达到跳出局部最优解的目的。改进后的算法在10个Benchmark函数上进行测试,实验结果表明改进后的算法效果明显优于增强烟花算法。
关键词 :增强烟花算法,模拟退火,自适应爆炸半径,差分变异

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
烟花算法(Fireworks Algorithm, FWA) [1] 是近年来新提出的群体智能算法,其思想来源于生活中的烟花爆炸过程。FWA同其他群智能算法类似,产生初始种群后,经过爆炸、变异、选择等操作产生下一代个体。
烟花算法自2010年谭营教授提出来就吸引了越来越多的科研工作者的研究,其中对传统烟花算法的改进分为两个方面:一是对烟花算法的四个算子进行分析和改进;二是和其它进化算法互补结合成混合算法。Pei [2] 等人利用烟花算法迭代过程中产生的爆炸火花和高斯变异火花等的种群位置和适应值信息对目标函数的搜索空间形状进行估计,为算法提供启发式加速信息。Tapas Si [3] 等人构造了一种新的计算烟花爆炸数目和幅度的方法,达到控制烟花爆炸数量、算法的开发性和探索性等效果。Zheng [4] 等人针对烟花算法性能上存在的缺陷,给出了对应的改进方法和策略,提出了增强烟花算法(Enhanced Fireworks Algorithm, EFWA)。Zheng [5] 等人提出动态烟花算法,即将烟花种群按适应度值的优劣划分成核心烟花和非核心烟花,并对核心烟花的爆炸半径进行自适应地调整来改善搜索性能。Li [6] 等人提出自适应烟花算法,即一种自适应爆炸半径机制,能够根据搜索结果进行自适应调节。Yu [7] 等人提出带有差分变异算子的新型烟花算法,以增加种群的多样性。Zheng [8] 等人将烟花算法和差分算法结合起来形成一种有效的混合算法,种群多样性增加达到跳出局部最优的效果。Zheng [9] 等人为了克服核心烟花比非核心占有绝对优势以及高斯变异算子不够有效的缺陷,通过提出合作框架即一种独立选择的方法提高开发能力,结合避免拥挤的合作策略提高搜索能力。Zhang [10] 等人提出基于生物地理学优化的烟花算法,即在三个方面提高烟花算法的交互能力:新的变异算子提高烟花的学习能力;爆炸操作中引入BBO的偏移算子,增强信息共享能力;新的选择策略使好的个体有更大的几率被选择到下一代。Li [11] 等人在烟花算法中引入引导火花(GS),增强算法信息的利用率,同时构建一个有方向和有自适应长度的指导向量(GV)形成精英解决方案,大大加强了烟花算法的探索和开发能力。Gao [12] 等人提出文化烟花算法在烟花爆炸中获取相应的知识,保存在知识库中,使个体能够学习知识库中的经验。
增强烟花算法是一种已被证明能够解决优化问题的不错算法,但在某些函数上寻优精度低、且容易过早地寻找到局部最优解,本文对增强烟花算法进行改进,提出一种自适应爆炸半径和差分变异的增强烟花算法(SAEFA)。将最大爆炸半径设置为模拟退火因子,来自适应地调节其搜索过程,使前期有利于全局搜索而后期有利于局部搜素。并在变异的过程中借鉴差分变异中的思想以增加种群的多样性,达到跳出局部最优解的目的。
本文的组织结构如下:第2章介绍增强烟花算法;第3章详细讨论最大爆炸半径为模拟退火因子和变异方式为差分变异以及算法的总流程;第4章为实验设置和结果分析;第5章总结全文。
2. 增强烟花算法
假设增强烟花算法 [4] 所求解的单目标无约束优化问题式子如下:
(1)
其中 为可行域。假设烟花的个数为 ,求解的函数为 维,则初始化时在 内随机产生 个烟花作为初始解,其中 表示第 个烟花的位置。通过对初始烟花进行爆炸操作、变异操作和选择操作得到下一代个体,直到找到函数的全局最优点。
2.1. 爆炸算子
增强烟花算法产生子代的方式是,在 个烟花附近的规定区域内使用爆炸操作生成新的火花。先确定第 个爆炸火花数量 和爆炸的半径 :
(2)
(3)
其中 和 为常数; 为一个非常小的数;若 表示个体 的适应函数值;则:
为了避免爆炸操作产生烟花的数量太多或太少,限制每个烟花产生的数量:
(4)
其中, 是第 烟花最终产生的烟花个数; 表示四舍五入取整函数; 和 为给定的常数。
为了避免适应度值最小的烟花由于爆炸半径太小而发挥不出挖掘的作用。增强烟花算法引入最小爆炸半径检测策略,则在维度 上烟花 的爆炸半径设置为:
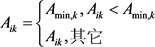 (5)
(5)
其中, 是在第 维上的爆炸半径最低的阈值,有两种不同的选择策略,其中非线性递减爆炸半径检测策略为:
(6)
烟花的爆炸首先要确定每个烟花爆炸的半径和产生火花的数量。同时在爆炸的过程中,烟花会进行相应的位移操作。不同于传统烟花算法产生火花时在每个维度具有相等的位移偏移。增强烟花算法在烟花产生火花的过程中在各个维度各个不同位置产生位移偏移来增加种群的多样性。
2.2. 变异操作
为了避免高斯变异时在原点位置附近产生很多火花,导致最优值为原点的测试函数占优,EFWA提出的变异操作为在当前解 和当前种群中最好的个体 之间进行变异,其计算公式为:
(7)
其中, 为高斯随机变量,其均值和方差分别为0和1。
2.3. 映射规则
EFWA为了避免原始烟花算法造成智能加速收敛的假象,提出一种随机映射规则,其公式为:
(8)
其中, 是在0到1区间上的均匀分布随机数。
2.4. 选择策略
增强烟花算法提出一种精英-随机选择策略,即首先从烟花、爆炸火花、高斯变异火花中选择一个适应度值最低的个体,再从剩下的烟花中随机选择 个烟花,共同作为下一代烟花种群的烟花。
3. 自适应爆炸半径和差分变异的增强烟花算法
SAEFA是在EFWA的基础上改进的。它们的不同之处是改进的算法将最大爆炸半径设置为模拟退火因子,并且借鉴了差分变异的思想将新型高斯变异方式变为差分变异方式。改进的算法由爆炸算子、变异操作和选择操作组成,同时为了防止越界也使用了映射规则。
3.1. 最大爆炸半径的设置
EFWA中将最大爆炸半径设置为常数,这将造成算法后期精细搜索能力被减弱,使算法的求解精度不高。受到动态搜索思想的启发,若最大爆炸半径总体上呈现出非线性递减的变化趋势,算法前期将有利于全局搜索,后期则有利于局部搜索,达到自适应加速的效果。
本文将最大爆炸半径设置为模拟退火因子。模拟退火 [13] 的思想受固体退火过程的启发,先让固体内部的温度升至充分高,当温度升高时,固体内的颗粒会随着温度上升变成无序状态,内能变大;再让固体逐渐冷却,颗粒随着温度降低渐趋有序而达到平衡态,最终下降到常温时变成基态,内能降到最小。其算法步骤为:
Step1:初始温度 ,初始解状态 ,每个 值的迭代次数 ;
Step2:对 执行Step3至Step6;
Step3:产生新解 ;
Step4:计算增量 ,其中 为评价函数;
Step5:若 ,则新解为 ,否则以概率 接受 为新的当前解;
Step6:终止条件满足则输出 作为最优解;
Step7: 逐渐减少趋于0,转至Step2。
设 为初始最大爆炸半径, 为当前迭代次数, 为最高的迭代次数,则第 个烟花最大爆炸半径公式为:
(9)
因此最大爆炸半径为模拟退火因子的烟花爆炸半径公式为:
(10)
3.2. 变异操作
在EFWA中,变异算子非常重要。通过变异操作,一个烟花不仅可以在其附近的位置搜索,甚至可以在其较远的位置产生火花进行搜索。受到差分进化(Differential Evolution, DE) [14] 中变异算子的启发,在SAEFA的进化中引入差分向量,再增加随机扰动,具体如下。
在子群中随机选择两个解 和 ,其差分向量记为 ,其值越小,扰动越小,每次变异进行如下操作:
(11)
其中 为当前代中适应度值最优的个体, 和 为缩放因子,本文实验中取 为1, 为0.03。
3.3. 基于模拟退火和差分变异的搜索策略
SAEFA沿用了EFWA计算爆炸火花的数量公式,采用同样的爆炸火花产生方式和选择策略,而采用公式(10)计算爆炸半径和采用公式(11)进行变异操作。SAEFA的基本流程如下:
Step1:初始时随机生成 个烟花的位置;
Step2:计算所有烟花的适应度值;
Step3:循环执行a至e,直到满足终止条件;
a:使用公式(2)和(4)计算烟花个数;
b:使用公式(10)计算烟花的爆炸半径;
c:生成爆炸火花;
d:使用公式(11)生成变异火花;
e:用选择策略选择 个个体进入下一代;
Step4:输出最优个体的位置和其适应度值。
4. 实验设置和结果分析
为了比较分析SAEFA的性能,本文将SAEFA算法、FWA算法和EFWA算法用于10个典型的Benchmark函数 [15] [16] 上进行测试,并对实验结果进行对比。Benchmark函数如表1所示。由于一些函数的名称太长,这里用符号表示。其中 表示Six-Hump-Camel-back函数, 表示Axis parallel-hyper-ellipsoid函数, 表示Rotated-hyper-ellipsoid函数。*代表此函数有好几个最优点。
4.1. 实验设置
由于选取的Benchmark函数中的许多函数的全局最优点在原点附近,烟花算法由于高斯变异在原点附近有很强的搜索能力。SAEFA因此为测试函数集使用了位置偏移,不同优化问题的搜索区域位置偏移也不同,如表2所示,其中 与 是优化问题的搜索范围。
仿真实验使用的平台是MATLAB2014a,为了使对比实验更加有效,三种算法采用相同的参数设置:初始时生成5个烟花,种群规模为50,变异个数为5,函数的评估次数最大设置为300,000,在同一条件下独立运行50次。
Table 1. Benchmark functions
表1. Benchmark函数
Table 2. The position of the Benchmark functions
表2. Benchmark函数的位置偏移
4.2. 实验结果分析
为了分析SAEFA的效果,在同一条件下,三个算法对表1中的10个Benchmark函数进行实验仿真,对每个位置偏移索引,下面给出函数平均最优值的表格,如表3到表12所示。
由表3至表7,表11,表12可知,FWA在无位置偏移的时候均能取得最优值,但是随着位置发生偏移,函数的仿真值越来越偏离最优值。而SAEFA和EFWA在所有测试函数中随着位置的偏移而不会发生太大影响,均能保持稳定。而在表4,表6和表12中,EFWA没有找到测试函数的最优解,进入局部最优。表8和表9显示SAEFA、EFWA和FWA三个算法均能够随着位置的偏移保持非常好的性能,都寻找到 函数和Goldstein Price函数的全局最优值。
Table 3. Comparison of global optimal mean of Sphere function (SI is offset index)
表3. Sphere函数全局最优平均值的对比(SI为偏移索引)
Table 4. Comparison of global optimal mean of Schwefel function (SI is offset index)
表4. Schwefel函数全局最优平均值的对比(SI为偏移索引)
Table 5. Comparison of global optimal mean of Ackley function (SI is offset index)
表5. Ackley函数全局最优平均值的对比(SI为偏移索引)
Table 6. Comparison of global optimal mean of Griewank function (SI is offset index)
表6. Griewank函数全局最优平均值的对比(SI为偏移索引)
Table 7. Comparison of global optimal mean of Penalized function (SI is offset index)
表7. Penalized函数全局最优平均值的对比(SI为偏移索引)
Table 8. Comparison of global optimal mean of F 1 ( x ) function (SI is offset index)
表8. 函数全局最优平均值的对比(SI为偏移索引)
Table 9. Comparison of global optimal mean of Goldstein-Price function (SI is offset index)
表9. Goldstein-Price函数全局最优平均值的对比(SI为偏移索引)
Table 10. Comparison of global optimal mean of Schaffer function (SI is offset index)
表10. Schaffer函数全局最优平均值的对比(SI为偏移索引)
Table 11. Comparison of global optimal mean of F 2 ( x ) function (SI is offset index)
表11. 函数全局最优平均值的对比(SI为偏移索引)
Table 12. Comparison of global optimal mean of F 3 ( x ) function (SI is offset index)
表12. 函数全局最优平均值的对比(SI为偏移索引)
上图的10个小图分别给出了3个算法对于10个Benchmark函数的进化曲线。为了更加清晰地展示各种算法的性能差异,图像纵坐标为函数适应值差取以10为底的对数值。如图1所示,SAEFA在Sphere函数中快速找到最优值,而在Schwefel函数中取得比EFWA和FWA较精确的值;如图2所示,SAEFA在Generalized Griewank函数中取得比EFWA和FWA较精确的值,在Ackley函数中虽然寻找的最优值与函数实际最优值有些差距,但是从迭代趋势来看,如果给出足够的迭代次数,最终还是可以找到最优值;如图3、图4和图5所示,SAEFA在 和Goldstein函数中均能够快速找到最优值,而在penalized、 和 函数取得比EFWA和FWA较精确的值。总体来看,SAEFA在10个测试函数中均表现出不错的效果。
5. 总结
增强烟花算法对某些函数寻优精度低,容易过早地陷入局部最优解,本文提出一种自适应爆炸半径和差分变异的增强烟花算法(SAEFA)。通过将最大爆炸半径设置为模拟退火因子自适应地加速算法搜索
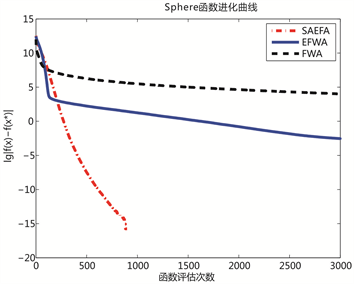
Figure 1. Convergence curves of Sphere and Schwefel functions
图1. Sphere和Schwefel函数进化曲线
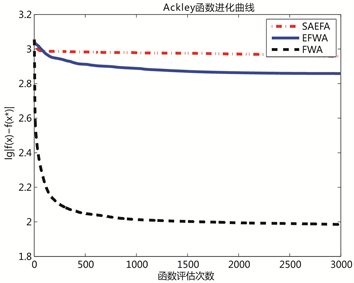
Figure 2. Convergence curves of Ackley and Generalize-Griewank functions
图2. Ackley和Generalize-Griewank函数进化曲线
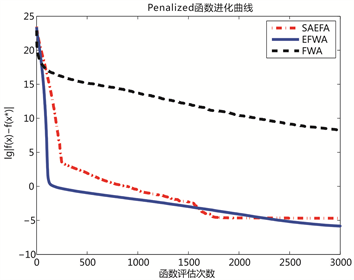
Figure 3. Convergence curves of Penalized and functions
图3. Penalized和 函数进化曲线
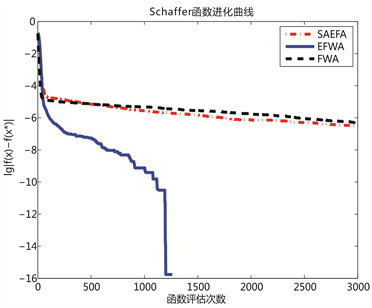
Figure 4. Convergence curves of Goldstein and Schaffer functions
图4. Goldstein和Schaffer函数进化曲线
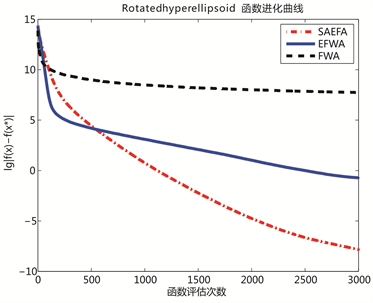
Figure 5. Convergence curves of and functions
图5. 和 函数进化曲线
过程,使算法迭代过程中全局搜索和局部搜索能力之间能够平衡,提高搜索性能。同时变异操作时借鉴差分变异的思想引入差分变异,使种群的多样性增加更有机会跳出局部区域。并在10个Benchmark函数中进行仿真实验,与EFWA和FWA进行对比,表明SAEFA能够随着位置偏移保持良好的性能,并且取得不错的搜索效果。
致谢
感谢导师温洁嫦老师在写作期间给予我的指导和鼓励,还有感谢刘海林老师的指导,感谢同门的陪伴和关怀。
基金项目
广州市科技计划项目(502150155)。
文章引用
叶雯雯,温洁嫦. 自适应爆炸半径和差分变异的增强烟花算法
Enhanced Fireworks Algorithm with Adaptive Explosion Amplitude and Differential Variation[J]. 应用数学进展, 2018, 07(02): 152-162. http://dx.doi.org/10.12677/AAM.2018.72019
参考文献 (References)
- 1. Tan, Y. and Zhu, Y. (2010) Fireworks Algorithm for Optimization. International Conference on Advances in Swarm Intelligence. Springer-Verlag, 355-364.
- 2. Pei, Y., Zheng, S., Tan, Y. and Hideyuki, T. (2012) An Empirical Study on Influence of Approximation Approaches on Enhancing Fireworks Algorithm. 2014 IEEE International Conference on Systems, 1322-1327.
https://doi.org/10.1109/ICSMC.2012.6377916 - 3. Si, T. and Ghosh, R. (2015) Explosion Sparks Generation Using Adaptive Transfer Function in Firework Algorithm. 2015 IEEE International Conference on Signal Processing, Communication and Networking, 1-9.
https://doi.org/10.1109/ICSCN.2015.7219917 - 4. Zheng, S., Janecek, A. and Tan, Y. (2013) Enhanced Fire-works Algorithm. 2013 IEEE Congress on Evolutionary Computation (CEC), 2069-2077.
https://doi.org/10.1109/CEC.2013.6557813 - 5. Zheng, S.Q., Janecek, A., Li, J.Z. and Tan, Y. (2014) Dynamic Search in Fireworks Algorithm. 2014 IEEE Congress on Evolutionary Computation (CEC), 3222-3229.
https://doi.org/10.1109/CEC.2014.6900485 - 6. Li, J., Zheng, S. and Tan, Y. (2014) Adaptive Fireworks Algo-rithm. 2014 IEEE Congress on Evolutionary Computation (CEC), 3214-3221.
https://doi.org/10.1109/CEC.2014.6900418 - 7. Yu, C., Li, J. and Tan, Y. (2014) Improve Enhanced Fireworks Algorithm with Differential Mutation. IEEE International Conference on Systems, Man and Cybernetics. IEEE, 264-269.
- 8. Zheng, Y.J., Xu, X.L., Ling, H.F. and Chen, S.Y. (2015) A Hybrid Fireworks Optimization Method with Differential Evolution Operators. 3rd International Conference on Swarm Intelligence (ICSI), 75-82
- 9. Zheng, S.Q., Li, J.Z., Janecek, A. and Tan, Y. (2016) A Cooperative Framework for Fireworks Algorithm. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 1-14.
- 10. Zhang, B., Zheng, Y.J., Zhang, M.X., et al. (2017) Fireworks Algorithm with Enhanced Fireworks Interaction. IEEE/ACM Transactions on Computational Biology & Bioinformatics, 14, 42.
https://doi.org/10.1109/TCBB.2015.2446487 - 11. Li, J., Zheng, S. and Tan, Y. (2017) The Effect of Information Utilization: Introducing a Novel Guiding Spark in the Fireworks Algorithm. IEEE Transactions on Evolutionary Computation, 21, 153-166.
https://doi.org/10.1109/TEVC.2016.2589821 - 12. Gao, H. and Diao, M. (2011) Cultural Firework Algorithm and Its Application for Digital Filters Design. International Journal of Modelling Identification & Control, 14, 324-331.
https://doi.org/10.1504/IJMIC.2011.043157 - 13. 赵晶, 唐焕文, 朱训芝. 模拟退火算法的一种改进及其应用研究[J]. 大连理工大学学报, 2006, 46(5): 775-780.
- 14. Storn, R. and Price, K. (1997) Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. Journal of Global Optimization, 11, 341-359.
https://doi.org/10.1023/A:1008202821328 - 15. Liang, J., Nsuganthan, P. and Ghernandez Diaz, A. (2013) Problem Definitions and Evaluation Criteria for the CEC2013 Special Session on Real-Parameter Opti-mization.
- 16. Liang, J.J., Qu, B.Y. and Nsuganthan, P. (2014) Problem Definitions and Evaluation Criteria for the CEC2013 Special Session and Competition on Single Objective Real-Parameter Numerical Optimization.
