ABSTRACT

In this paper, through the support function of strictly closed convex curves, the one-dimensional inverse mean curvature flow is transformed into partial differential equations. Using Lies point symmetry group theory, the symmetry group of one-dimensional inverse mean curvature flow is studied, and the equations are reduced. The group has no solution.

Keywords:Inverse Mean Curvature Flow, Support Function, Symmetry Group, Invariant Solution

一维逆平均曲率流的对称群及 不变解

薛美乐

聊城大学，山东 聊城

收稿日期：2018年5月22日；录用日期：2018年6月12日；发布日期：2018年6月19日

摘 要

本文通过严格闭凸曲线的支撑函数，将一维逆平均曲率流转化成偏微分方程，利用李点对称群理论，研究了一维逆平均曲率流的对称群，并对方程进行约化，讨论了群不变解。

关键词 :逆平均曲率流，支撑函数，李点对称群，不变解

Copyright © 2018 by author and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

本文主要采用不变群理论研究了一个从逆平均曲率流中推导出的非线性方程的群不变解问题。关于逆平均曲率流的研究，已有很多结果，如2012年，丁琪研究了平均曲率流的自相似解和一类逆平均曲率流 [1] ；2014年，刘艳楠和苏梅研究了一类带外立场的逆平均曲率流的梯度估计 [2] ；2015年，陈邦彦对逆平均曲率流进行了研究 [3] 。李对称群方法是研究几何和物理领域中微分方程不变解的基础方法.李群又称对称群或不变群，它是数学中应用及其广泛的一个分支，李群与微分方程的联系由来已久，随着非线性微分方程研究的需要，通过微分方程的不变性来研究非线性偏微分方程的性质，特别是方程的不变解已成为一个十分重要的课题.为了求解微分方程的群不变解，首先要确定微分方程的李点对称群及其子群.

本文将研究如下一维逆平均曲率流的对称群及不变解，方程如下：

$\frac{\partial r}{\partial t}=-k^{-1}n.$ (1.1)

其中： $\gamma$ 是闭严格凸曲线， $k^{-1}$ 是平面曲线 $\gamma$ 的逆平均曲率，向量 $n$ 是平面曲线 $\gamma$ 的单位内法向量。

本文首先利用凸曲线函数的支撑函数，将一维逆平均曲率流转化成简单的抛物型偏微分方程。其次利用Olver提出的方法 [4] 系统的研究了抛物型偏微分方程，求解出该方程的对称代数，最后根据得到的对称性的相关向量，通过对称约化方法 [4] 得到抛物型偏微分方程的群不变解。

2. 抛物型偏微分方程的导出

微分几何是运用微积分理论研究空间的几何性质，古典微分几何研究三维空间中的曲线和曲面，而现代微分几何开始研究更一般的空间流形，微分几何学以光滑曲线(曲面)作为研究对象，关于这方面的研究，已经建立了一个比较完整的体系。在过去的几十年中，数学家、物理学家以及天文学家对时空中的曲线和曲面的运动越来越感兴趣，这方面的研究也取得了很大的进展，其中最重要的例子就是平均曲率流：

$\frac{\partial \gamma }{\partial t}=kn.$ (2.1)

这种流是抛物的，它是抛物型偏微分方程理论在几何中的成功应用，这一部分我们将研究如下一维逆平均曲率流：

$\frac{\partial r}{\partial t}=-k^{-1}n$ (*)

其中： $\gamma$ 是闭严格凸曲线，k是平面曲线 $\gamma$ 的平均曲率，向量 $n$ 是平面曲线 $\gamma$ 的单位内法向量。上述方程可以简化成曲线的支撑函数所满足的偏微分方程。

假设 $\gamma :h^1\times \left[0,t\right)\to R^2$ 是一族满足(*)的凸曲线族，我们用法向角参数化演化曲线 $\gamma \left(\cdot ,t\right)$ ，用曲线的支撑函数研究流的短时间存在性。

取 $\tilde{\gamma }\left(\theta ,\tau \right)=\gamma \left(u\left(\theta ,\tau \right),t\left(\theta ,\tau \right)\right)$ 。其中 $t\left(\theta ,\tau \right)=\tau$ ， $\frac{\partial \tilde{\gamma }}{\partial \tau }=\frac{\partial \gamma }{\partial u}\frac{\partial u}{\partial \tau }+\frac{\partial \gamma }{\partial t}$ 。

由链式法则可得

$0=\frac{\partial \theta }{\partial \tau }=\frac{\partial \theta }{\partial u}\frac{\partial u}{\partial \tau }+\frac{\partial \theta }{\partial t}.$

定义演化曲线 $\tilde{\gamma }\left(\theta ,\tau \right)=\left(x\left(\theta ,\tau \right),y\left(\theta ,\tau \right)\right)$ 的支撑函数为

$h\left(\theta ,\tau \right)=\langle \tilde{\gamma }\left(\theta ,\tau \right),-n\rangle =x\left(\theta ,\tau \right)\cos \left(\theta \right)+y\left(\theta ,\tau \right)\sin \left(\theta \right).$

那么我们有

$h_{\theta }\left(\theta ,\tau \right)=\langle \tilde{\gamma }\left(\theta ,\tau \right),t\rangle =-x\left(\theta ,\tau \right)\sin \left(\theta \right)+y\left(\theta ,\tau \right)\cos \left(\theta \right),$

则曲线 $\tilde{\gamma }$ 可由支撑函数及其支撑函数关于法向角的一阶偏导数给出

$\{\begin{array}{l}x\left(\theta ,\tau \right)=h\cos \left(\theta \right)-h_{\theta }\sin \left(\theta \right),\\ y\left(\theta ,\tau \right)=h\sin \left(\theta \right)+h_{\theta }\cos \left(\theta \right).\end{array}$

通过直接计算可得

$h_{\theta \theta }+h=-x_{\theta }\sin \left(\theta \right)+y_{\theta }\cos (\theta )$

$\frac{\text{d}\gamma }{\text{d}s}\frac{\text{d}s}{\text{d}\theta }=\left(\frac{\text{d}\gamma }{\text{d}s}\frac{\text{d}s}{\text{d}\theta },t\right)=\frac{\text{d}s}{\text{d}\theta }.$

由Frenet-Serret公式，我们有

$h_{\theta \theta }+h=\frac{1}{k}$

$h_{\tau }=\langle \frac{\partial \tilde{\gamma }}{\partial \tau },-n\rangle =\langle \frac{\partial \gamma }{\partial u}\frac{\partial u}{\partial \tau }+\frac{\partial \gamma }{\partial t},-n\rangle =\langle \frac{\partial \gamma }{\partial t},-n\rangle =k^{-1}=h_{\theta \theta }+h.$ (2.2)

这是一个偏微分方程，根据偏微分方程的理论，可以得到方程(*)解的局部存在唯一性定理。

3. 抛物型偏微分方程(2.2)的对称群

李对称方法是研究偏微分方程的有效工具，一个偏微分方程的对称群是作用在自变量和因变量空间上最大的连通局部李氏变换群，并且它把方程的一个解映射到另一个解，即保持了解集的不变性。我们以2阶偏微分方程为例。

下面我们将会给出偏微分方程(2.2)的对称群，则方程为：

$h_{\tau }-h_{\theta \theta }=h$ (3.1)

设

$X=\xi \left(t,\theta ,h\right)\frac{\partial }{\partial t}+\eta \left(t,\theta ,h\right)\frac{\partial }{\partial \theta }+\varphi \left(t,\theta ,h\right)\frac{\partial }{h}.$

是在开集 $M\subset D\times U$ 上的一个 $c^{\infty }$ 向量场。对方程(2.2)而言，不变条件有如下形式：

$-\varphi +{\varphi }^{\tau }-{\varphi }^{\theta \theta }=0.$

将 ${\varphi }^{\tau },{\varphi }^{\theta \theta }$ 的具体形式代入上式，并利用方程(3.1)，消去 $h_{\theta \theta }$ ，即用 $h_{\tau }-h$ 来代替 $h_{\theta \theta }$ ，我们就可以得到如下等式：

$\begin{array}{c}0=-\varphi +{\varphi }_{\tau }+\left({\varphi }_h-{\xi }_{\tau }\right)h_{\tau }-{\eta }_{\tau }{h}_{\theta }-{\xi }_h{h}_{\tau }^2-{\eta }_h{h}_{\tau }{h}_{\theta }-{\varphi }_{\theta \theta }-\left(2{\varphi }_{\theta h}-{\eta }_{\theta \theta }\right)h_{\theta }+{\xi }_{h\tau }\\ -\left({\varphi }_{hh}-2{\eta }_{\theta h}\right)h_{\theta }^2+2{\xi }_{\theta h}{h}_{\tau }{h}_{\theta }+{\eta }_{hh}{h}_{\theta }^3+{\xi }_{hh}{h}_{\tau }{h}_{\theta }^2-\left({\varphi }_h-2{\eta }_{\theta }\right)\left(h_{\tau }-h\right)\\ +2{\xi }_h{h}_{\tau \theta }+3{\eta }_h{h}_{\theta }\left(h_{\tau }-h\right)+{\xi }_h{u}_{\tau }\left(h_{\tau }-h\right)+2{\xi }_h{h}_{\theta }{h}_{\tau \theta }.\end{array}$

把这个等式看成是函数h各阶偏导数的多项式，由于其各不相关，所以各阶偏导数的系数均恒等于零。于是，我们得到一个偏微分方程组。

$\begin{array}{l}-\varphi +{\varphi }_{\tau }-{\varphi }_{\theta \theta }=0,-{\xi }_{\tau }+{\xi }_{\theta }+2{\eta }_{\theta }=0,\\ -{\eta }_{\tau }-2{\varphi }_{\theta h}+{\eta }_{\theta \theta }=0,{\xi }_{\theta h}-{\eta }_h=0,\\ 2{\eta }_{\theta h}-{\varphi }_{hh}=0,{\eta }_{hh}=0,{\xi }_{hh}=0,\\ {\varphi }_h-2{\eta }_{\theta }=0,{\xi }_{\theta }=0,{\eta }_h=0,{\xi }_h=0.\end{array}$

它的通解为

$\begin{array}{l}\xi \left(\tau ,\theta ,h\right)=c_1,\\ \eta \left(\tau ,\theta ,h\right)=c_2,\\ \varphi \left(\tau ,\theta ,h\right)=c_3\cos \left(\theta \right)+c_4\sin \left(\theta \right).\end{array}$

其中 $c_1,c_2,c_3,c_4$ 是任意不相关常数，这样就得到了方程(3.1)的四维李点对称群，这组通解定义了方程(3.1)的对称群。

定理3.1 方程

$h_{\tau }=h_{\theta \theta }+h$

的对称群所对应的李代数由以下向量场生产：

$\begin{array}{l}{v}_1=\frac{\partial }{\partial \tau },v_{\text{2}}=\frac{\partial }{\partial \theta },\\ v_3=\sin \left(\theta \right)\frac{\partial }{\partial h},v_4=\cos \left(\theta \right)\frac{\partial }{\partial h}.\end{array}$

下面验证向量场 $\left\{v_1,v_2,v_3,v_4\right\}$ 关于李括号运算是封闭的，见表1。

由此不难解出与上列向量场相应的单参数群如下。

$\begin{array}{l}{g}_1:\left(\tau ,\theta ,h\right)\to \left(\tau +\epsilon ,\theta ,h\right),\\ g_2:\left(\tau ,\theta ,h\right)\to \left(\tau ,\theta +\epsilon ,h\right),\\ g_3:\left(\tau ,\theta ,h\right)\to \left(\tau ,\theta ,h+\epsilon \sin \left(\theta \right)\right),\\ g_4:\left(\tau ,\theta ,h\right)\to \left(\tau ,\theta ,h+\epsilon \cos \left(\theta \right)\right).\end{array}$

进一步，根据上述单参数不变群可知，若 $u=f\left(x,y\right)$ 是方程(3.1)的解，则下列 $u^{\left(1\right)},u^{\left(2\right)},u^{\left(3\right)},u^{\left(4\right)}$ 也是方程的解，即群不变解。

表1. 李括号运算

$\begin{array}{l}{u}^{\left(1\right)}=f\left(x-\epsilon ,y\right),\\ u^{\left(2\right)}=f\left(x,y-\epsilon \right),\\ u^{\left(3\right)}=f\left(x,y\right)+\epsilon \sin \left(y\right),\\ u^{\left(4\right)}=f\left(x,y\right)+\epsilon \cos \left(y\right).\end{array}$

4. 方程(3.1)的对称约化和群不变解

我们在求出非线性偏微分方程(3.1)的向量场后，接下来根据所求出的无穷小生成子得到偏微分方程的约化方程，往往这些约化方程比原非线性偏微分方程容易求解，进而给出了 $v_1+c{v}_2,v_3,v_4$ 情形下得不变解。

4.1. $v_1+c{v}_2$ 情形

首先求解 $v_1+c{v}_2$ 对应的不变量 $\xi$ ，为求不变量，我们解 $v_1+c{v}_2$ 相应的特征方程，的特征方程为：

$\frac{\text{d}\tau }{c}=\frac{\text{d}\theta }{1}=\frac{\text{d}h}{0}$ (4.1)

解式(4.1)得到 $v_1+c{v}_2$ 的1个群不变量：

$\xi =\tau -c\theta$ (4.2)

从不变量(4.2)得到原方程(3.1)的不变解具有下面形式：

$h=f\left(\xi \right)$ (4.3)

由(4.3)式计算出关于 $\tau ,\theta$ 的各阶导数

$h_{\tau }=f^{\prime },h_{\theta }=-c{f}^{\prime },h_{\theta \theta }=-c{f}^{″}.$

把以上结果代入方程(3.1)得到以下常微分方程：

$f^{\prime }+c{f}^{″}=f$ (4.4)

4.2. v₃情形

首先求解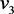对应的不变量 $\xi$ ，为求不变量，我们解 $v_3$ 相应的特征方程， $v_3$ 的特征方程为：

$\frac{\text{d}\tau }{0}=\frac{\text{d}\theta }{0}=\frac{\text{d}h}{\sin \left(\theta \right)}$ (4.5)

解式(4.5)得到 $v_3$ 的1个群不变量：

$\xi =\cos \left(\theta \right)$ (4.6)

从不变量(4.6)得到原方程(3.1)的不变解具有下面形式：

$h=f\left(\xi \right)$ (4.7)

由(4.7)式计算出关于 $\tau ,\theta$ 的各阶导数

$h_{\tau }=0,h_{\theta }=-\sin \left(\theta \right)f^{\prime },h_{\theta \theta }=-\cos \left(\theta \right)f^{\prime }-\sin \left(\theta \right)f^{″}.$

把以上结果代入方程(3.1)，得到以下常微分方程：

$\cos \left(\theta \right)f^{\prime }+\sin \left(\theta \right)f^{″}=f.$ (4.8)

4.3. v₄情形

首先求解 $v_4$ 对应的不变量 $\xi$ ，为求不变量，我们解 $v_4$ 相应的特征方程， $v_4$ 的特征方程为：

$\frac{\text{d}\tau }{0}=\frac{\text{d}\theta }{0}=\frac{\text{d}h}{\cos \left(\theta \right)}$ (4.9)

解式(4.9)得到 $v_4$ 的1个群不变量：

$\xi =-\sin \left(\theta \right)$ (4.10)

从不变量(4.10)得到原方程(3.1)的不变解具有下面形式：

$h=f\left(\xi \right)$ (4.11)

由(4.11)式计算出关于 $\tau ,\theta$ 的各阶导数

$h_{\tau }=0,h_{\theta }=-\cos \left(y\right)f^{\prime },h_{\theta \theta }=\sin \left(\theta \right)f^{\prime }-\cos \left(\theta \right)f^{″}.$

把以上结果代入方程(3.1)，得到以下常微分方程：

$-\sin \left(\theta \right)f^{\prime }+\cos \left(\theta \right)f^{″}=f$ (4.12)

5. 结论

在这篇文章中，我们系统地研究了一个从逆平均曲率流中推导出的非线性方程的群不变解问题，利用李点对称群理论，研究了一维逆平均曲率流的对称群。通过对方程进行约化，我们能将原偏微分方程化为较之简单的常微分方程，从而得出了原方程的群不变解，但本文对逆平均曲率流只是做了较初步讨论，还有许多问题有待我们去深入研究，在以后的工作中，我们将会更深入的研究，以期获得更多的结果和收获。

致谢

本文是在导师王增桂教授和同学丁冉的指导下进行撰写，从方程的选取，分析及解决都得到了导师的精心指导，在论文完成之际，我郑重的感谢导师和同学对我的指导和帮助。

文章引用

薛美乐. 一维逆平均曲率流的对称群及不变解
Symmetrical Groups and Invariant Solutions of One-Dimensional Inverse Mean Curvature Flows[J]. 应用数学进展, 2018, 07(06): 667-672. https://doi.org/10.12677/AAM.2018.76079

参考文献