Advances in Applied Mathematics
Vol.
08
No.
02
(
2019
), Article ID:
28782
,
5
pages
10.12677/AAM.2019.82021
Application of Transfer Learning in Data Analysis and Fault Diagnosis of Ultrasonic Flowmeter
Jing Zhao, Wenqiang Luo, Keke Deng
School of Mathematics and Physics, China University of Geosciences, Wuhan Hubei
Received: Jan. 12th, 2019; accepted: Jan. 27th, 2019; published: Feb. 3rd, 2019

ABSTRACT
As an important industrial measuring equipment, ultrasonic flowmeter is widely used in fluid detection. Flowmeters with different designs collect different characteristics and generate a large amount of data at every time, every minute and every place. These data have different similarities and structures. Traditional machine learning cannot efficiently use such data. This kind of problem requires transfer learning method. In this paper, we deal with similar data generated by different flowmeters, transfer learning under the condition of higher data similarity, and obtain better results.
Keywords:Ultrasonic Flowmeter, Transfer Learning, TrAdaBoost
迁移学习在超声波流量计数据分析 及故障诊断上的应用
赵静,罗文强,邓珂珂
中国地质大学,数学与物理学院,湖北 武汉
收稿日期:2019年1月12日;录用日期:2019年1月27日;发布日期:2019年2月3日

摘 要
超声波流量计作为一种重要的工业计量设备,被广泛应用在流体检测方面。不同设计的流量计采集不同的特征,在每时每分每处产生大量的数据,这些数据相似度不一、结构不定。传统的机器学习无法高效处理这种不同分布的学习,需要应用迁移学习方法。本文使用迁移学习处理不同流量计产生的类似数据,在数据相似度较高的情况下进行了迁移学习,实验获得了较好的效果。
关键词 :超声波流量计,迁移学习,TrAdaBoost

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着信号采集和信息处理技术的日趋成熟,超声波技术被广泛运用在生产生活当中,超声波流量计就是超声波技术在工业上的重要应用 [1] 。国际以及国内天然气工业的快速发展,天然气管道的监测与维护成为大家的关注的焦点,如何高效处理超声波流量计测得的大量数据,及时发现管道故障,是本文旨在研究的问题。
传统的机器学习需要一定数量的好的样本用以训练出可靠的模型,而不同流量计产生的实际数据往往是不同分布的,甚至是不同构的,这种情况下,需要进行迁移学习。迁移学习能够利用少量的有标签训练样本(某些场景下不利用任何有标签训练样本),辅以源领域数据,建立一个相对可靠的模型,用于目标领域数据的预测 [2] 。
基于实例的迁移学习的基本思想是 [3] ,在有少量目标领域训练数据的情况下,尽管这些训练数据和源领域的训练数据实际上并不相同,从整体上看表现出较大差异,但是对于样本个体而言,某些训练数据与目标领域的训练数据相似度较高,这些与目标领域相似度较高的训练数据能够促进目标领域的学习,用以训练分类模型并适应测试数据。
2. 算法介绍
基于实例的迁移学习方法的核心就是从源领域的训练数据中找出那些适合目标领域的样本实例,在TrAdaBoost算法中,我们通过更新样本权重完成实例的删选:有利于目标领域学习的,即加入之后能够提高目标领域分类准确度的,此类训练样本的权重将会增加,反之权重将会减小。
基于实例的迁移学习的目标就是从源领域的训练数据中找出那些适合目标领域的实例,并将这些实例迁移到源训练数据的学习中去。这个过程,我们通过更新样本权重来完成,有利于目标领域学习的,即加入之后能够提高目标领域分类准确度的,此类训练样本的权重将会增加,反之权重将会减小。
TrAdaBoost算法更新权重过程如下 [4] :
输入:源领域训练数据集 (n条训练数据),目标领域训练数据集 (m条训练数据),训练数据集 ,测试数据集S,分类器 ,迭代次数N。
初始化:
1、初始权重向量 ,其中,
2、初始 值
权重更新
For
1、归一化权重 ,
2、利用带权数据计算得到分类器 ,计算该分类器在 上的错误率 ,
3、 。
更新权重
3. 实例研究
3.1. 数据来源
本文所使用的超声波流量计数据来自UCI机器学习数据库 [5] ,数据具体信息如表1。
Table 1. Data information
表1. 数据信息
从表1中,我们可以看出仪表C和仪表D具有相同的数据结构,即具有相同的特征数、分类数。使用matlab绘制仪表C和仪表D的第一个特征数据的核函数密度函数曲线,如图1。从仪表C、仪表D和两者的混合数据中分别随机抽取100组数据计算MMD距离,得到表2。结合图表分析,我们可以看出两组数据虽然有相同的数据结构,其数据分布仍然有不可忽视的差异。
3.2. 实验结果
仪表C与仪表D的原始数据每一行有44个属性值,其中前43个属性值代表采集的参数值,最后一个属性值代表分类结果,被选为标签集。使用迁移学习算法计算结果如表3所示:
4. 结论
数据分布不一致的情况会严重影响传统的机器学习性能,将C、D组这两组不同的数据进行混合,
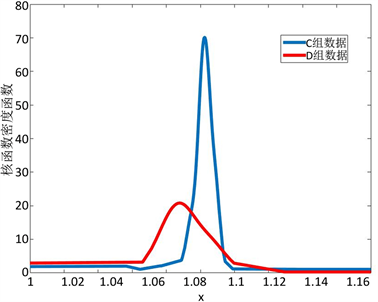
Figure 1. Kernel density function curve
图1. 核函数密度函数曲线
Table 2. MMD result
表2. MMD距离结果表
Table 3. Tradaboost result
表3. 迁移学习计算结果表
对比传统的机器学习方法,在相同数据上进行线性SVM分类学习,其精度如表4所示。
Table 4. Traditional machine learning results
表4. 传统机器学习计算结果表
在这样的混合数据上进行分类学习,平均精度仅为72.37%,且稳定性较差,算法的最低精度低至53.87%,最高精度和最低精度差别超过30%。当源领域和目标领域的样本数据分布不一致时,如果仍然将这样的迁移学习问题视为普通机器学习,将会产生不可控制的误差,选取C组数据进行训练在D组数据上进行检测,最低精度低至0,选取D组数据进行训练在C组数据上进行检测,最低精度低至21.25%。使用迁移学习之后,分类精度有了大幅度提高,平均精度超过80%,稳定性更为优良,算法精度标准差明显降低。
文章引用
赵 静,罗文强,邓珂珂. 迁移学习在超声波流量计数据分析及故障诊断上的应用
Application of Transfer Learning in Data Analysis and Fault Diagnosis of Ultrasonic Flowmeter[J]. 应用数学进展, 2019, 08(02): 188-192. https://doi.org/10.12677/AAM.2019.82021
参考文献
- 1. 陈鹏, 任霖钦, 蒋安荔. 超声波流量计诊断及故障处理[J]. 石化技术, 2016, 23(3): 133.
- 2. 庄福振, 罗平, 何清, 史忠植. 迁移学习研究进展[J]. 软件学报, 2015, 26(1): 26-39.
- 3. 戴文渊. 基于实例和特征的迁移学习算法研究[D]: [硕士学位论文]. 上海: 上海交通大学, 2009.
- 4. 张倩, 李海港. 基于知识表达的迁移学习方法及其应用[M]. 徐州: 中国矿业大学出版社, 2015: 36-39.
- 5. Ultrasonic Flowmeter Diagnostics Data Set. http://archive.ics.uci.edu/ml/datasets/Ultrasonic+flowmeter+diagnostics#
