Advances in Applied Mathematics
Vol.
08
No.
08
(
2019
), Article ID:
31615
,
6
pages
10.12677/AAM.2019.88155
L2 Solutions of BSDEs with a New Kind of Non-Lipschitz
Shiyu Li, Liping Dan, Lufan Yang
Faculty of Science, Jiangxi University of Sciences and Technology, Ganzhou Jiangxi

Received: Jul. 15th, 2019; accepted: Aug. 1st, 2019; published: Aug. 8th, 2019

ABSTRACT
The classical backward stochastic differential equation (BSDE) is driven by the Brownian motion, but Brownian motion is a very special stochastic process, so the application of backward stochastic differential equation is quite limited. In this paper, we are interested in solving one-dimensional backward stochastic differential equations (BSDEs) with a new kind of non-Lipschitz coefficients [1] . We establish an existence and uniqueness result of solutions in L2.
Keywords:Backward Stochastic Differential Equation, Continuous Local Martingale, Non-Lipschitz, Existence, Uniqueness
一种新非Lipschitz条件下倒向随机微分方程的L2解
李师煜,但李萍,杨璐帆
江西理工大学理学院,江西 赣州

收稿日期:2019年7月15日;录用日期:2019年8月1日;发布日期:2019年8月8日

摘 要
经典的倒向随机微分方程是由布朗运动驱动的,但布朗运动是一种非常特殊的随机过程,致使倒向随机微分方程的应用受到相当大的限制。本文研究了以连续局部鞅为干扰源的一维倒向随机微分方程,在生成元满足一种新非Lipschitz条件下 [1] ,证明了其L2解存在且唯一。
关键词 :倒向随机微分方程,连续局部鞅,非Lipschitz条件,存在性,唯一性

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
倒向随机微分方程在金融数学、最优控制、随机决策和偏微分方程等领域中有着广阔的应用前景。经典的倒向随机微分方程是由布朗运动驱动的,1990年Pardoux和Peng [2] 给出了Lipschitz条件下解的存在唯一性结果。然而Lipschitz条件太强,布朗运动太过于理想化,致使倒向随机微分方程的应用受到相当大的限制。因此,一方面,许多学者开始研究各种非Lipschitz条件下的倒向随机微分方程来改进Pardoux和Peng的关于解的存在唯一性,例如,Fan [1] ,Mao [3] ,Lepeltier和Martin [4] ,Kobylanski [5] 分别给出了非Lipschitz条件下解的存在唯一结果。另一方面,有相当多的学者研究了其他干扰源驱动的倒向随机微分方程,其中,李娟 [6] 研究了连续局部鞅驱动的Lipschitz条件下的倒向随机微分方程,王湘君 [7] 研究过由连续半鞅驱动的Lipschitz条件下的倒向随机微分方程。本文中,我们研究了由连续局部鞅驱动的倒向随机微分方程在Fan [1] 中非Lipschitz条件下解的存在唯一性。
2. 主要结果
令 为一个带信息流的完备的概率空间,其中流 满足通常条件,记 为可料 σ 域。 为一个连续局部鞅,并且 , 为M的平方变差过程。 为一个任意固定的数,称为时间区间。
首先给出几个相关记号:
1) 用 表示所有使得 的 -适应的 值的过程 的集合。当 时简记为 。
2) 用 表示所有使得 的 可料的 值的过程 的集合。当 时简记为 。
3) 用
表示所有满足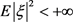 的
-可测的
值的随机变量
的集合。当
时简记为
。
的
-可测的
值的随机变量
的集合。当
时简记为
。
以下,我们将讨论如下形式的一维倒向随机微分方程:
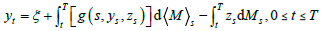 (1)
(1)
其中, 为 适应的过程, 为 可料的过程, , 为具有零初值的连续局部鞅,具有可料表示性,且 为有界的,即存在正常数 ,使得 ,a.s.,函数 为 可测的。
假设方程(1)满足以下条件:
(H1) ;
(H2) 存在一个单调不减凹函数 ,使得 , ,
其中 , , 。
(H3)存在一个常数 ,使得 , ,
(H4) ;
注1: 是一个单调不减凹函数,且 ,即 几乎处处是线性增长的,存在一个常数 ,使得对 ,有 。
定理1 设函数g满足(H1)—(H4), ,则倒向随机微分方程(1)在 中有唯一的解。
3. 引理
为了证明定理1,我们还需要用到下面的引理。我们首先来构造倒向随机微分方程(1)的Picard逼近序列,由如下的倒向随机微分方程所定义:
, (2)
其中,生成元 满足(H3)和(H4),由文献 [8] 定理4.2得,对 ,方程(2)在 中有唯一的解 。
由注1和(H2),容易得
和
引理1 在定理1的假设下,存在一个常数 和常数 ,且 只依赖于C,K只依赖于C和T,
使得对任意的 , n,m ≥ 1 ,有
(3)
和
(4)
证明:由方程(2),得 是如下方程(5)在 中的解
(5)
其中 。
由(H2)和(H3),得
(6)
(6)式意味着方程(5)的生成元 满足文献 [1] 命题1中的假设(A),即 , , , 。又因为 是一个凹函数,所以由文献 [1] 命题1和命题2,应用Fubini定理和
Jensen不等式,即可得(3)式和(4)式。 证毕。
引理2 在定理1的假设下,存在一个不依赖于 的 ,常数 ,使得对 ,有 。
证明:由定理1的假设,得
即方程(2)的生成元 满足文献 [1] 命题1中的假设(A)。
又因为 是一个凹函数,所以由文献 [1] 命题2,应用Fubini定理和Jensen不等式,存在两个只依
赖于C的正常数 和 ,使得对 ,有
(7)
其中
令
,
,其中
是引理1中的,A是注1中的,则对 ,有
,有
(8)
由(7)和(8),得
(9)
又因为 是一个单调不减函数,由(9)式,注1和(8)式,得 ,
,证毕。
4. 定理1的证明
先证存在性。先定义一个函数列 如下:
(10)
对 ,由引理2,得
,
,
。
由数学归纳法,可得
。
因此,对 ,函数列 极限存在,记为 。
因为 是一个连续函数,且 ,令 ,对(10)式取极限,由Lebesgue收敛定理,对 ,有
,
,
。
由数学归纳法,可得
即 是cauchy序列,又因为 是一个连续函数,由引理1中的(4)式知, 也是cauchy序列,它们的极限分别记为 和 。令 ,对(2)式取极限,可得 是具有参数 的BSDE在 的 解。
可以通过迭代可得,
,方程(1)在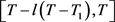 有解,因此可得,方程(1)在
上解的存在性。
有解,因此可得,方程(1)在
上解的存在性。
再证唯一性:设
和
都是方程(1)的
解,则

是如下方程(11)的 解。
(11)
其中, 。
由(H2)和(H3),可得
,即方程(11)的生成元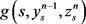 满足文献 [1] 命题
满足文献 [1] 命题
1中的假设(A)。
由文献 [1] 命题1和命题2,存在一个只依赖于C的正常数 和一个只依赖于C和T的正常数 ,使
得对 ,有
(12)
和
。 (13)
对(12)式应用Bihari’s不等式,得 ,因此 ,再由(13)式,又可得 ,唯一性得证。
基金项目
国家自然科学基金资助项目(11561028,11801238),江西省教育厅青年科学基金资助项目(GJJ170566,GJJ170567,GJJ170525),江西理工大学大学生创新创业训练项目(DC2018-072),江西理工大学本科教学工程项目(XZG-16-01-05)。
文章引用
李师煜,但李萍,杨璐帆. 一种新非Lipschitz条件下倒向随机微分方程的L2解
L2 Solutions of BSDEs with a New Kind of Non-Lipschitz[J]. 应用数学进展, 2019, 08(08): 1321-1326. https://doi.org/10.12677/AAM.2019.88155
参考文献
- 1. Fan, S.J. and Jiang, L. (2014) Lp Solutions of BSDEs with a New Kind of Non-Lipschitz Coefficients. Mathematics, arXiv: 1402.6773.
- 2. Pardoux, E. and Peng, S. (1990) Adapted Solution of a Backward Stochastic Differential Equation. Systems Control Letters, 14, 55-66. https://doi.org/10.1016/0167-6911(90)90082-6
- 3. Mao, X. (1995) Adapted Solution of Backward Stochastic Differential Equations with Non-Lipschitz Coefficients. Stochastic Processes and Their Applications, 58, 281-292. https://doi.org/10.1016/0304-4149(95)00024-2
- 4. Leltier, J.P. and Martin, J.S. (1997) Backward Stochastic Differential Equation with Continuous Coefficient. Statistics & Probability Letters, 32, 425-430.
- 5. Kobylanski, M. (2000) Backward Stochastic Differential Equations and Partial Differential Equations with Quadratic Growth. The Annals of Probability, 18, 259-276.
- 6. 李娟. 一般鞅驱动的倒向随机微分方程[J]. 山东大学学报(理学版), 2005, 40(4): 70-76.
- 7. 王湘君. 由连续半鞅驱动的倒向随机微分方程[J]. 数学杂志, 1999, 19(1): 45-50.
- 8. Briand, P., Delyon, B., Hu, Y., Pardoux, E. and Stoica, L. (2003) Lp Solutions of Backward Stochastic Differential Equations. Stochastic Processes and Their Applications, 108, 109-129. https://doi.org/10.1016/S0304-4149(03)00089-9