Advances in Applied Mathematics
Vol.
08
No.
12
(
2019
), Article ID:
33310
,
16
pages
10.12677/AAM.2019.812220
Taxi Assignment Problem in the Airport Based on Queue Theory
Handan Yu, Luxin Zhou, Yuqing Shi, Huizeng Zhang, Anshui Li*
Department of Mathematics, School of Science, Hangzhou Normal University, Hangzhou Zhejiang

Received: Nov. 9th, 2019; accepted: Nov. 28th, 2019; published: Dec. 5th, 2019

ABSTRACT
In this paper, the taxi assignment problem in the airport is studied based on queue theory. Firstly, we consider all the corresponding factors of decision-making of taxi-driver and the mechanics of this problem in a whole, and give one mathematical model for the drivers based on queue theory, as well as the strategies under different conditions. Secondly, we give some optimization for the taxi assignment system in the airport based on the model mentioned above, and establish one model named multi-point single-assignment system. Compare with the data from Pudong Airport, our model is relatively feasible and useful.
Keywords:Queue Theory, Utility Function, Sensitivity Coefficient, Decision-Making of Driver Model, Taxi-Assignment Model
基于排队论的机场出租车调度问题研究
于晗丹,周璐鑫,施雨晴,张慧增,李安水*
杭州师范大学理学院数学系,浙江 杭州

收稿日期:2019年11月9日;录用日期:2019年11月28日;发布日期:2019年12月5日

摘 要
本文旨在研究基于排队论的机场出租车调度问题。首先,本文通过对影响出租车司机决策的相关因素进行了机理分析,综合考虑各相关因素,建立了基于排队论的司机决策模型,并给出了司机的相应选择策略。同时,运用基于排队论的决策模型对机场出租车载客系统进行优化,得到了多点单独发车的机场载客区出租车分配模型。最后,通过与浦东机场相关数据进行分析对比,我们的模型具有较强的合理性和指导性。
关键词 :排队论,效用函数,敏感系数,司机决策模型,机场分配模型

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
出租车司机在将乘客送达到机场后,将会面临两个选择:
(A) 前往机场的“蓄车池”。由于需要排队等待排在前面的出租车离开和等待乘客前来乘车,因此,需要付出一定的时间成本来载客。
(B) 不前往“蓄车池”,直接空车返回市区拉客。但是会带来空载和损失掉可能存在的载客收益。
司机是否选择载客与他的个人经验有关,司机可以获得航班到达数据以及机场“蓄车池”里所排队的出租的数量。如果司机选择去载客,需要由机场管理员“分批定量”放入“乘车区”。而需要搭乘出租车的乘客会自行前往“乘车区”进行排队。
结合实际情况,要求建立数学模型来解答以下问题:
1) 构建一个关于出租车司机的决策模型,给出司机选择的策略;
2) 结合上海浦东机场的相关数据以及上海的出租车数量,根据获取的数据,确定司机的选择策略;
3) 对两条并行车道合理设置“上车点”,并对乘客和出租车进出“乘车区”进行合理安排,在保证司机和乘客的安全的条件下,实现整体的乘车效率达到最大;
4) 具体化“优先权”的规则,弥补载短途的司机的收益损失,让机场的出租车司机的收益尽量保持均衡。
2. 模型假设
1) 假设蓄车池规模无限大,允许车辆无限排队。
2) 假设不计出租车车重变化及突发路况急刹车等特殊情况对每公里油耗的变化。
3) 假设不考虑突发事件对乘客上车时间的影响。
4) 假设短途返程的司机均将乘客送达目的地,不存在中途放客。
3. 符号说明
我们给出本文中所用到的符号及其说明,见表1。
Table 1. The symbols
表1. 相关符号
4. 模型的建立与求解
4.1. 基于排队论的出租车司机决策模型
4.1.1. 影响出租车司机决策因素的机理分析
随着经济的不断发展,往返机场的乘客人数大幅上涨,其中大多数乘客下飞机后选择出租车作为去往目的地的主要交通工具之一。对于送客到机场的出租车司机都面临着两个亟需做出的选择。因为出租车行业主要是以营利为目的,并且由题目知道司机可以得到某时间段抵达的航班数量和“蓄车池”里已有的车辆数等信息。假设出租车司机均为理性人,他们在做出最终方案选择的时候总是追求利润最大化的,因此我们通过权衡收益和成本,建立以利润最大化为目标的决策模型。
4.1.2. 决策因子的分析
通过机理分析,司机可以对A、B方案可获得利润进行判断,根据利润比较,对A、B方案进行决策,选择是否进入“蓄车池”。我们经过分析,得到了影响利润的主要因素包含收益和成本,此外,结合实际情况发现影响成本的主要因素有空载费用、载客费用、潜在收益和时间成本。因此将空载费用、载客费用、潜在收益、时间成本以及收益作为一级指标,又通过具体分析得到出租车司机选择的决策因子关系图,如下图1所示。
以下是各个决策因子的建立:
1) 收益R
出租车收益R由出租车的载客行驶里程和每公里收费价格得到
(1)
其中 为出租车载客行驶里程, (元/km)为出租车每公里收费价格, 为载客行驶时间。
2) 空载费用E
出租车空载费用是指出租车没有搭乘乘客时行驶所消耗的费用。由于出租车在行驶过程中的最大耗费在汽油上,对于车体的损耗难以定量估计,所以出租车空载费用E为
(2)
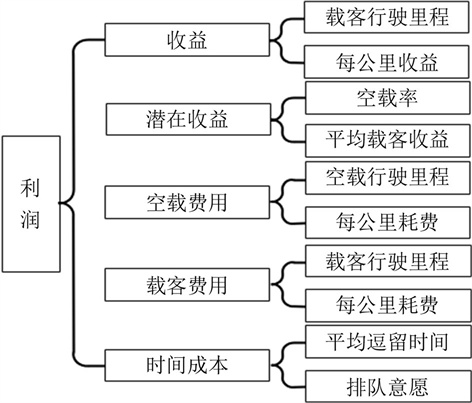
Figure 1. Decision system diagram
图1. 决策体系图
其中 为出租车空载行驶里程,u(元/km)为出租车每公里成本, 为空载行驶时间。
3) 载客费用F
出租车载客费用是指出租车在搭乘乘客时行驶所消耗的费用。同样,由于出租车在行驶过程中最大耗费在汽油上,对于车体的损耗难以定量估计,所以出租车载客费用F为
(3)
其中 为出租车载客行驶里程,u(元/km)为出租车每公里成本。
4) 潜在收益
出租车在直接放空返回市区拉客的情况下可能会损失潜在的载客收益。这里我们把可能会损失的潜在的载客收益叫做潜在收益 ,跟潜在收益紧密相连是潜在的载客可能性。而与载客可能性相关的另一个因素是空载率,空载率即为没有搭乘乘客的出租车在所有营行车中的百分比,往往出租车的空车率越大,出租车接到客的概率就越小。故潜在收益为
(4)
其中, 是出租车空载率, 为载客的平均收益。
5) 时间成本
时间成本不仅是时间上的损失,也指在等待时间内造成的市场机会的流失。在本文的实际背景中,有时候可能会出现由于机场乘客数量较少或者乘客上车速度较慢导致的排队载客情况。此时,司机在这段等待时间中就会产生相应的时间成本。所产生的时间成本
数学公式如下:
(5)
其中 为司机平均排队接客逗留时间, (元/h)为出租车司机单位时间内收益。
下面对司机平均排队接客逗留时间 进行求解:
为计算司机平均排队接客逗留时间 可以将出租车排队载客看作一个动态、离散、随机的排队系统。因此我们选择使用排队论 [1] 对其进行求解。
1) 输入过程
我们假设蓄车池空间大小无限,允许无限排队。且出租车单独到达上车点接客。另外出租车到达蓄车池时间服从参数为 的负指数分布,乘客上车时间(即出租车离开乘车区时间)服从参数为 的负指数分布。
2) 排队规则
出租车在单车道依次排队等候,先到先接客;乘客为单条排队队列候车,先到先上车。
3) 服务台
假设仅有一个上车点,即出租车为单车道依次排队等候。且乘客为单条排队队列候车,假设一辆车仅搭载一位乘客,具体情况如下图2所示。
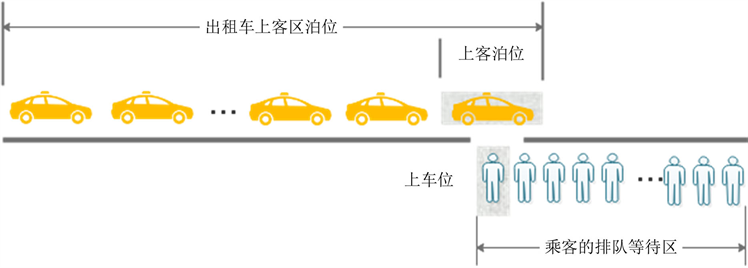
Figure 2. Service desk diagram
图2. 服务台示意图
于是可通过建立单服务台等待制模型(即M/M/1/∞)来求解出租车司机排队接客逗留时间 。
记 为出租车载客系统达到平衡状态后队长L的概率分布,由于每个状态下出租车到达上车点时间都是独立的,乘客上车时间同样也是独立的,因此有 和 。
记 由于在平稳状态下队长的分布为
(6)
其中
(7)
故
(8)
则得到平均队长
(9)
可以证明出租车司机在该排队系统中的接客逗留时间 服从参数为 的负指数分布,则出租车司机排队接客逗留时间 概率分布为
(10)
故理论上平均逗留时间 。
其中 表示单位时间平均到达蓄车池的车辆数, 表示单位时间离开乘车区的辆数。由于司机可知晓某时间段“蓄车池”里已有的车辆数以及抵达航班数量,因此司机在做出决策时,也会受到个人意愿的影响,为了综合定量、直观地描述司机个人主观判断的强弱,又由于当司机得知抵达的乘客数与“蓄车池”里已有的车辆数之比大于1时,司机愿意排队,则单位时间平均到达蓄车池的车辆数相对增多;反之,司机犹豫排队,则单位时间平均到达蓄车池的车辆数相对增少。因此我们通过建立关于“蓄车池”里已有的车辆数以及抵达的乘客数的效用函数Q作为排队意愿,来调节平均逗留时间所造成的损失。效用函数Q的具体数学表达式如下:
(11)
其中n为某时间段内乘客人数,N为某时间段内蓄车池中已有的车辆数。
综上,我们确定在实际情况下,平均逗留时间
(12)
4.1.3. 司机选择决策模型的建立及策略的提出
根据上述决策因素的机理分析以及对各决策因子的分析,权衡收益和成本,得到利润
表达式如下:
(13)
当选择A方案时,司机在“蓄水池”等待载客后再返回市区,这会造成一定的时间成本。但是选择A方案的司机不会产生空载费用以及潜在收益的损失,故对于A方案的利润中 、E均为0,即
(14)
当选择B方案时,由于司机送客到机场后空车返回市区,因此基本不会造成排队现象产生时间成本,也就不会有时间成本的损失,即 。但是司机在选择B方案的同时需要承担返回市区的空载成本和可能存在的潜在收益,即
(15)
由于出租车司机在选择方案的时候,总是以利润最大化为目标,因此我们通过对比在相同时间段内方案A、B的利润,建立出租车司机选择决策模型Y即
(16)
为了进一步为出租车司机提出选择策略,我们对相同时间段内A、B方案所获得的利润做差进行研究。
对于方案A,在固定时间段t内的获得的利润为
(17)
其中, 代表选择方案A所产生的出租车司机的收益, 代表选择方案A产生的载客费用, 代表在方案A条件下出租车载客行驶里程。
对于方案B,在固定时间段t内的获得的利润为
(18)
其中, 代表选择方案B所产生的出租车司机的收益, 代表选择方案B产生的载客费用, 代表在方案B条件下出租车载客行驶里程。
公式(17)~公式(18)得到
(19)
由于时间t相同,于是有
(20)
其中, 、 分别表示方案A、B载客行驶时间, 表示方案B的空载时间。
进而化简公式(19),得到
(21)
其中, 表示机场到市中心的平均距离。
由于在同一路程中所花费的成本一定小于所获得的收益,因此 的系数一定小于0,
故当
时, ,即当机场乘客数量较多且满足上述关系式时,出租车司机选择方案A润更大,而相反,当机场乘客数量较少时,出租车司机选择方案B利润更大。
4.2. 司机决策模型的实际应用与分析
4.2.1. 数据收集与处理
在选择机场的过程中,我们发现上海浦东机场有着特别的优势。第一,上海作为世界一线城市,在数据整合收集的广度、深度以及频率要远远高于国内大部分城市。第二,上海浦东机场作为一个国际化大机场,有着较为完善的数据储备和较为先进的路侧交通管理模式。第三,在我们寻找到具有真实性和可靠性的资料中,上海浦东机场可获得资料量较多,所以我们选择收集上海浦东机场和其城市所在的出租车的相关数据。
根据问题一中所建立的出租车司机选择决策模型,结合所给的司机选择策略、收集到的上海浦东机场2015~2018年各月份的旅客吞吐量 [2]、机场旅客乘坐出租车的占比、上海浦东机场距离市中心的距离以及上海市出租车市区内行驶速度与收费标准及其成本等数据(具体数据见附件)。
整理我们所收集的数据,根据需求进行筛选处理,得到模型所需数据。其中,结合上海出租车公司官网数据得到,上海市大部分出租车车型为桑塔纳4000,该车使用的汽油价格约为6.60元/L。通过经验判断得到出租车每行驶10 km大约消耗汽油1升汽油,由此确定出租车行驶每公里的油耗成本为0.66元/km。结合问题一对空载和载客费用的分析得到,出租车行驶每公里费用0.66元。由于上海市区的主干道路的限速主要为30、40 km/h,所以我们把出租车行驶速度设为35 km/h。计算得上海浦东机场距离市中心的距离的平均距离大于15公里,结合上海市出租车收费标准,为了便于计算,我们取出租车收费标准为3.6元/公里。
相关数据如下表2所示:
Table 2. The data of relevant parameter
表2. 相关参数数据
另外,根据相关资料 [3] 显示,在浦东机场,一天中约有25%的到港旅客需要乘坐出租车离开机场,因此根据浦东机场2015~2018年各月份的旅客吞吐量计算得到浦东机场2015~2018年不同月份单位时间的旅客乘坐出租车的人数如下表3所示。
Table 3. Number of passagers in Shanghai Pudong International Airport per month from 2015 to 2018
表3. 上浦东机场 2015~2018 年不同月份单位时间的乘客数
4.2.2. 上海浦东机场出租车司机选择方案的确立
根据问题一中所建立的出租车司机的决策模型,将处理后的数据带入公式(21)得到A方案较B方案的利润
(22)
又因为 ,其中 ,n为机场乘客数,N为蓄车池已有车辆。
化简得到
(23)
然后我们可以通过带入2015~2018年不同月份单位时间的旅客乘坐出租车的人数估算出不同月份单位时间的旅客乘坐出租车的人数n,由于司机可以通过观测得到“蓄车池”中已有的车辆数N,所以我们可以通过带入已知的n,计算当 取临界值0时,N的取值,向该机场出租车司机提出合理的选择性方案。具体方案如下:
司机首先通过经验判断得出大致的乘客人数,然后通过选择决策模型计算得到临界的“蓄车池”车辆,当司机得到的已在“蓄车池”的车辆未超过临界值时,司机选择A方案,超过临界值时,则选择B方案。如表4所示是司机在指定月得到的“蓄车池”临界值,当“蓄车池”中已有的车辆数N值大于当月的临界值时,则选择方案B,即放客后直接返回。反之,则选择方案A,即前往“蓄车池”等待载客。
Table 4. Circle value of storage tank of cars every month
表4. 各月蓄车池车辆临界值
4.2.3. 模型对相关因素的依赖性和模型合理性评价
从问题一的分析得到影响决策的一级指标和二级指标,由于一级指标是通过二级指标推导得到的,这里我们进行模型对相关因素依赖性的探究。我们采取敏感性分析 [5] 来探究模型对相关因素的依赖性。操作方案如下:
1) 在不改变其他因素数据的情况下,选择一个二级指标进行改动。
2) 由于司机在做出决策时考虑的是将利润最大化,所以我们分别求出指标改动后的方案A利润PA和方案B利润PB进行作差,得出方案A较方案B的利润差。
3) 计算方案A较方案B利润的相对变动,并将其与二级指标数据的相对变动做比,得到利润对该指标变动的敏感系数,推导模型对该指标的依赖性。
如下是模型对各个二级指标的依赖性探究。首先,通过参考上海浦东机场的相关数据,选取各个指标初始值如下表5所示:
Table 5. Initial value of index
表5. 指标初始值
以每公里收益为例,将每公里收益上调20%后,通过司机选择决策模型分别得到Rs变动前后的方案 A、B利润,计算得到方案A较方案B利润的相对变动L为
(24)
其中, 为变动后A方案利润, 为变动后的B方案利润。
将方案A较方案B利润的相对变动L与每公里收益的相对变动20%做比,得到方案A较方案B利润对每公里收益的敏感系数 。
(25)
通过MATLAB,求解得到方案A较方案B利润对每公里收益的敏感系数 为0.985。表6是方案A较方案B利润对各个因素的敏感系数。
Table 6. Sensitivity coefficient of profit of plan A to various factors compared with plan B
表6. 方案A较方案B利润对各个因素的敏感系数
从表中可以看出出租车在“蓄车池”平均逗留时间 越长,出租车单位时间收益Rt越高,车速越快,方案A较方案B的利润就越小,司机选择方案B的概率就越大。当载客行驶里程Sf越多,空车率El越高,每公里收益Rs、平均收益 越高,每公里耗费u越高,方案A较方案B的利润就越大,司机选择A的概率就越大。其中,出租车在“蓄车池”平均逗留时间,行驶里程对司机选择方案的敏感度均较高。空车率、每公里收益、平均收益、出租车每公里、单位时间收益、车速、每公里收益对司机选择方案的敏感度均较低。此外,载客行驶里程对司机选择方案的敏感度最高,每公里收益对司机选择方案的敏感度最低。
通过表6,我们可以得出司机决策对模型中的指标因素变化敏感,模型对指标的依赖性较强,说明决策模型的建立的指标选取比较合理。并且,通过实际推导,各指标对司机决策的正负影响及影响大小符合实际,模型较为合理。
4.3. 上车点及发车模式的确立
在某些时候,由于出租车数量和乘客数量的供求不平衡以及机场交通管理模式不当,容易导致“车等人”或“人等车”的现象发生。为缓解此问题,我们通过文献查阅以及资料搜集,发现常见的机场出租车接客上车点设置主要有单点依次式 [6]、多点依次发车式 [7] 以及多点单独发车式 [8] 这三种方式。但综合考虑资源成本以及效率,总结出适用于两条并行车道的乘车区,大致有2种上车点的设置方式,即两点依次发车模式以及多点单独发车模式。我们分别对这两种方式进行分析比较,得出最合理的上车点的设置方案。同时为使得乘车效率达到最高,再通过合理安排泊车位,最终通过考虑以出租车排队时长与乘客排队时长组合而成的排队系统时长最小化为目标,得出最合理的安排方案。
4.3.1. 两点依次发车模式
两点依次发车模式的出租车接客系统是指乘车区内将两个上车点分别设置在两个车道的尽头,乘客仅拥有一个公共排队通道,当排队结束后分别到这两个上车点上车,其布局示意图如下图3所示。这样使得同一时间内发车数量增加,因此在某种情况下提高了乘车效率。但由于两点依次发车模式容易引起人车冲突,从而耽误内侧道出租车发车时间,降低乘车的总的效率。因此出于时间利用和乘客及车辆的安全考虑,两点依次发车模式并不能使得乘车效率达到最高,并存在一定的安全隐患。
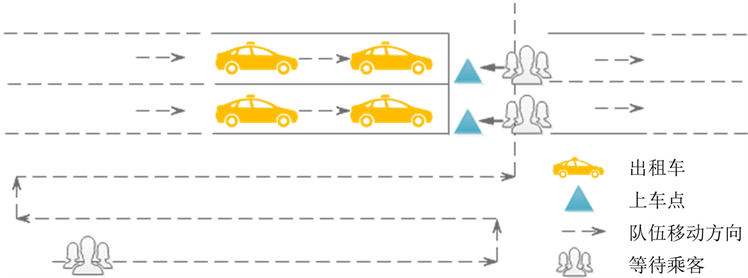
Figure 3. Two points taxi queuing system
图3. 两点依次发车式出租车排队服务系统示意图
4.3.2. 多点单独发车模式
多点单独发车模式的出租车接客系统是指乘客拥仅有一个公共排队通道,但有多个上车点,且每个上车点分别对应一辆出租车,于是该模式可以看成M/M/n排队模型,其布局示意图如下图4所示。其中内车道为载客停靠车道,当出租车完成服务后,随即转至外车道驶离乘车区,无需按照依次驶离的原则,因此出租车在乘车区的等待时间仅与乘客上车时间有关,故该种模式能够减少出租车等待时间,同时由于拥有多个上车点,因此可以通过实际乘客数以及车辆数,来合理调整上车点的开放数以及对应的管理人员数,从而降低管理成本、减少资源浪费。
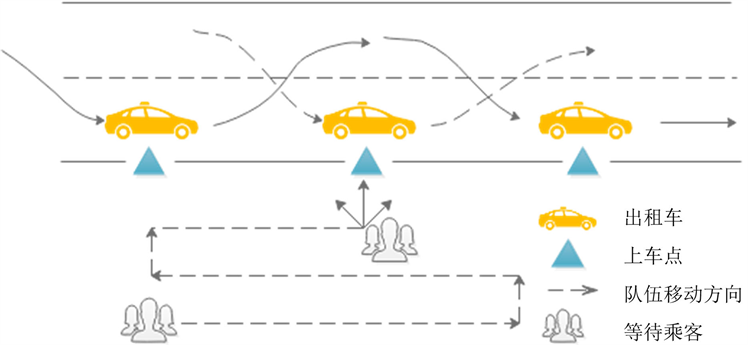
Figure 4. Multi points taxi queuing system
图4. 多点单车发车模式出租车排队服务系统示意图
根据上述分析,多点单独发车模式的乘车区排队模型属于M/M/n排队模型。在该系统达到稳态时,n个上车点并联发车,根据排队论的相关知识 [6],得知该系统的繁忙程度
(26)
推导出
(27)
从而求出该系统中乘客排队长度 的数学表达式如下
(28)
为使得总的乘车效率达到最高,需要减少乘客逗留时间(降低乘客等待用),同时提高服务水平(降低出租车等待费用),而服务水平与服务率 以及服务窗口数(上车点数n)有关。建立这两者的费用总和最小的优化目标,运用排队系统中的费用模型对多点单独发车模式排队系统进行优化来确定最优上车点数量。
假设乘客等待费用为 ,出租车等待费用 ,其中a为每个乘客单位时间的等待时间成本,b为每辆出租车等待时间成本,n表示上车点数。当两者之和达到最小时,系统为最优,建立以下目标规划:
(29)
即
(30)
本文中,我们采用问题二中搜集得到的上海浦东机场出租车乘车区的乘客到达率 与服务率 ,并假设乘客等待费用与出租车等待费用之比为1:400。
初始参数如下表7所示
Table 7. Initial parameter table
表7. 初始参数表
利用上述费用模型对某机场的出租车排队接客系统进行优化,得到以下计算结果
Table 8. Data of cost model calculation process
表8. 费用模型计算过程数据
由上述表8计算得到,当n = 4时,满足公式(30),即此时排队接客系统达到最优,可实现总的乘客效率最高。
参考资料 [9],可知路边停车位平行式排列时,平均每辆车的占据长约6米,因此综上分析求解,在保证乘客以及车辆安全的情况下,管理部门应在乘车区车道靠近乘客排队一侧并排设置四个上车点,两个上车点之间的距离为6米,并通过单独发车的方式进行接客。具体示意图5如下所示。
4.4. 出租车短途返程“优先权”方案设计
在人民网、长江日报等媒体报道上,机场短途乘客上车时被司机拒载,出租车司机排队一两小时只拉到收益微薄的短途这些事件屡屡出现。参考目前针对出现此类问题提出的解决方案,提出出租车短途返程“优先权”方案设计。
已知选择方案A的司机都需要经历排队,他们的时间成本相同。除此之外,他们的每公里耗费、每公里收益等指标数据也大致相同。我们以机场为圆心,以机场距离市中心的平均距离S为半径做如下图6。
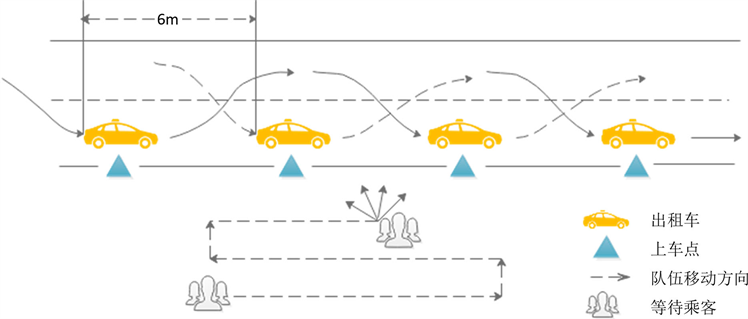
Figure 5. Multi points taxi queuing system
图5. 多点单车发车模式出租车排队服务系统示意图
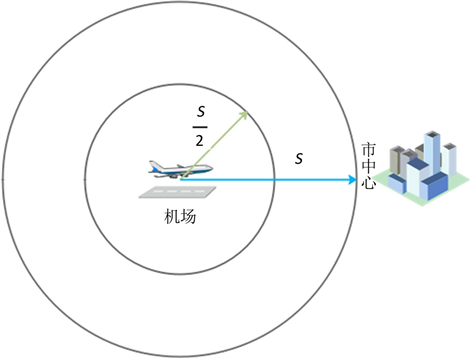
Figure 6. Taxi driving range
图6. 出租车行驶范围示意图
由于市中心人口密集,出租车需求量大,出租车司机一般更为愿意在市中心附近工作。故当司机驾驶出租车到距市中心距离小于距机场距离时,司机将不会选择返程。所以当司机接到的乘客前往的目的地属于图中半径为S/2的圆内,那么司机不但行驶的里程较短并且返程接客的意愿较大。因此当司机行驶的路程小于或等于S/2,我们视作此次接客为行驶里程为短途。
为了较好的判断该出租车是否接到短途乘客 [10],可以通过司机接到乘客离开机场到司机返回机场的时间间隔来判断。通过道路交通数据,可以知道城市道路限速v,则出租车司机短程往返的限制时间 为
(31)
当出租车往返的时间小于该限制时间,视作司机为短途返程,让他可以不用在“蓄车池”等待,直接排队进场载客。
下面以上海浦东机场为例,设计出租车短途返程“优先权”方案。
通过问题二的数据收集与处理,我们已经得到了上海浦东机场距市中心的距离约为47.61 km。又由于越靠近市中心道路的限速越严,车速越小,越偏离市中心道路的限速越宽,车速越大。在视作出租车短途的范围内道路大都为城市道路,限速为60 km/h左右,故浦东机场短途司机的往返限制时间 为0.7935小时。虽然在车辆行驶道路上出现行人,障碍物等影响行驶时间的可能性较小,但出于安全考虑,我们将出租车短途返程的限制时间适当调大,此时限制时间为0.83小时,也就是50分钟。
故对于上海浦东机场,为出租车短途返程设置的“优先权”方案为:当上海浦东机场的司机接到乘客后50分钟内返回机场,就给与他“优先权”,可以不用再“蓄车池”等待,直接进场载客。
5. 模型的评价
5.1. 优点
1) 本文所建立的模型均参考实际机场数据进行应用,可直观通过结果检验模型是否合理。
2) 将总的乘车效率最高问题转化为乘客平均等待时长和司机等待时长之和最小的指标规划问题,把握了主要矛盾的主要因素,舍弃了次要因素,从而简化了模型。
3) 在问题三中引入了排队论中的费用决策模型,对机场出租车接客系统进行优化,使得该系统中总的服务效率得到提升。
5.1. 缺点
1) 本文建立模型时考虑的情况皆适用于大规模机场,缺乏对机场规模较小情况的思考。
2) 在建立机场司机选择决策模型时,对于司机排队时间成本的计算固然合理,但仍有需要改进的地方。
6. 模型的评价
本文的机场司机选择决策模型同样适用于铁路出租车司机决策,并能推广到外卖、滴滴司机接单等需要进行选择决策的应用中。此外,本文对于短途返程司机的“优先权”方案安排可以借鉴到外卖抢单、司机抢单系统中,给予服务反馈较好或上一单收益较低的员工一定优惠,用以奖励或平衡其收益。
基金项目
浙江省自然科学基金(LQ18A010007),国家自然科学基金(11901145)。
文章引用
于晗丹,周璐鑫,施雨晴,张慧增,李安水. 基于排队论的机场出租车调度问题研究
Taxi Assignment Problem in the Airport Based on Queue Theory[J]. 应用数学进展, 2019, 08(12): 1905-1920. https://doi.org/10.12677/AAM.2019.812220
参考文献
- 1. 吴翊, 吴孟达, 成礼智. 数学建模的理论与实践[M]. 湖南: 国防科技大学出版社, 1999: 231-233.
- 2. 中国民用航空华东地区管理局. 华东地区机场运输生产情况[EB/OL]. http://hd.caac.gov.cn/HD_XXGK/HD_TJSJ/, 2016-04-27-2019-02-25.
- 3. 林思睿. 机场出租车运力需求预测技术研究[D]: [硕士学位论文]. 成都: 电子科技大学, 2018.
- 4. 广发证券. 公交II行业: 出租车深度报告[EB/OL]. https://doc.mbalib.com/view/4defa2e2a6e158cc1e649365a4ef40c0.html, 2015-09-18.
- 5. 姚飞. 公司利润敏感性分析及对策研究[D]: [硕士学位论文]. 哈尔滨: 黑龙江大学, 2018.
- 6. 姚丽君, 邵家玉. 基于地铁成本控制分析以提高运营效益的研究[J]. 科技资讯, 2010(32): 63-64.
- 7. 魏中华, 王琳, 邱实. 基于排队论的枢纽内出租车上客区服务台优化[J]. 公路交通科技(应用技术版), 2017, 13(10): 298-300.
- 8. 吴娇蓉, 李铭, 梁丽娟. 综合客运枢纽出租车上客点管理模式和效率分析[J]. 交通信息与安全, 2012, 30(4): 18-23.
- 9. 北京建筑工院. 汽车库建筑设计规范[M]. 北京: 中国建筑工业出版社, 2015.
- 10. 张隽, 关喜艳. 天河机场出租车短途返程优先配客[EB/OL]. http://hb.people.com.cn/n2/2019/0122/c194063-32559595.html, 2019-01-22.
NOTES
*通讯作者。
