Advances in Applied Mathematics
Vol.
09
No.
01
(
2020
), Article ID:
33744
,
12
pages
10.12677/AAM.2020.91003
Research on Optimization Algorithms of Single-Block Train Formation Plan on Railway Corridor
Xiaqi Wei1,2, Hanxiao Jiao1,2, Dongyue Liang1, Shurong Zhang1, Weihua Yang1*
1School of Mathematics, Taiyuan University of Technology, Jinzhong Shanxi
2Research Institute of Information Technology, Tsinghua University, Beijing

Received: Dec. 9th, 2019; accepted: Dec. 26th, 2019; published: Jan. 2nd, 2020

ABSTRACT
This paper studies the optimization problem of single-block train formation plan on railway corridor. Railway corridor is the backbone of the railway network. When applying the existing research results on train formation plan of general railway network to railway corridor, due to the characteristics of railway corridor itself and traffic flow are not fully considered in modeling, the computational resources consumption is large and the optimization effect is general. In order to solve the above problems, this paper establishes an optimization model of single-block train formation plan on the railway corridor with the time cost as the main optimization objective, and designs two iterative algorithms based on greedy strategy for the model. Numerical experiments show that, compared with the common genetic algorithm, the method adopted in this paper is faster and saves the time cost by more than 14% on average.
Keywords:Train Formation Plan, Railway Corridor, Integer Programming, Greedy Strategy

铁路货运通道上的单组列车编组计划优化算法研究
魏夏琦1,2,焦含笑1,2,梁东岳1,张淑蓉1,杨卫华1*
1太原理工大学数学学院,山西 晋中
2清华大学信息技术研究院,北京

收稿日期:2019年12月9日;录用日期:2019年12月26日;发布日期:2020年1月2日

摘 要
本文研究铁路货运通道上的单组列车编组计划优化问题。货运通道是铁路网络中的骨干网,将已有的关于一般铁路网络的列车编组计划的研究结果应用于铁路货运通道时,由于在建模时未充分考虑铁路货运通道本身的特点以及车流特征,算力资源消耗较大且优化效果一般。针对上述问题本文建立了以时间成本为主要优化目标的铁路货运通道上的单组列车编组计划优化模型,并且为该模型设计了两种基于贪婪策略的迭代算法。通过数值实验表明,与常用的遗传算法比较,本文所采用的方法运算时间更短,且平均优化效果提升14%。
关键词 :列车编组计划,铁路货运通道,整数规划,贪婪策略

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1.1. 背景介绍
本文研究货运通道上的单组列车编组计划问题。铁路货物运输的作业流程包括装车站的发送作业、途中运送以及卸车站的终到作业。与客运列车的固定车底不同,货运列车是由不同车辆编组构成的。列车编组计划规定了列车的编组内容,即如何将车流组织成列流。对于货运组织的途中运送环节,列车编组计划处于核心地位。目前我国铁路使用的列车编组计划由铁路总公司下发各铁路局执行,依年度更新。过长的更新间隔使得编组计划经常不能适应车流变化的情况,因此,依据车流状态正确编制和执行列车编组计划是充分发挥铁路运输能力,提高运输效率,尽可能满足运输市场需求的重要途径 [1] [2]。铁路货运通道是铁路网络的骨干网。货运通道的主要特点是:拓扑结构简单,货运量大,运输能力强,设备利用率高。虽然货运通道在整个路网里程当中占比不高,但是平均承担铁路货运周转总量的一半以上 [3] [4]。因此,研究货运通道上的列车编组计划对提高货物运输效率,减少货物运输成本具有重要意义。
关于编组计划优化问题的模型一般以经济成本,或者时间成本作为优化目标。以经济成本作为优化目标的主要问题在于与成本相关的关键参数,比如车辆中转费用、列车改编费用等,目前没有公认的可靠取值,只能依靠专家经验进行估值。因此使得整体模型的可靠性受到了限制。另一方面,由于在铁路货运过程中货物在车站内花费的时间约占全部运输时间的65%左右,以时间成本作为优化目标能够大大缩短货物运输时间,降低货物在运输过程中对于铁路设施资源的占用成本。另外,随着铁路技术作业标准化的推进使得各项技术操作耗时拥有统一标准,进而提升了各种时间花费参数的精准性。列车编组计划建模问题的难点在于,在一般情形下,经济成本最小化与时间成本最小化是相互矛盾的。为了降低经济成本会要求列车满轴开行,使得列车的集结时间增加,导致货物在站内的停留时间延长。反之,为了降低时间成本会要求列车定点开行,这样会产生列车欠轴现象,进而导致经济成本上升。综上,在设计列车编组计划优化模型时,需要在货物运输的迅捷性与经济性之间进行权衡考虑。有趣的是,当考虑货运通道上的列车编组计划时,这种矛盾是不存在的。原因在于货运通道上的车流量非常大,加快货物周转速度并不会造成列车欠轴。反之,如果货物周转速度较慢会造成站内拥堵,产生拥堵成本。因此,在货运通道上经济成本最优化与时间成本最优化具有一致性。
1.2. 相关工作
国内外学者对于技术站单组列车编组计划问题进行了大量的研究。Li Y H等 [5] 首先对货运列车编组计划编制的复杂性进行了描述,指出通过车流路线与编组方案的联合优化可以得到准确合理的结果。然后将货运列车编组计划问题转化为编组网络图的计算问题,建立数学模型使得铁路网内车流总成本最小。Marin等 [6] 以线路通过能力、车站改编能力、列车开行数量为限制条件,以列车开行成本、车流改编成本以及新增设施投资费用总和最小为目标函数构建了整数规划模型,并采用下降法、模拟退火算法和禁忌算法对模型进行求解。Ahuja R K等 [7] 提出货运编组问题是为网络中所有调车场的所有装运确定分类计划,以最小化总装运成本创建编组计划,使用超大规模邻域搜索实现解决方案所需的各种实际约束和业务约束。朱松年 [8] 针对货运编组计划的优化问题建立非线性0-1规划模型,使用模拟退火算法获得接近全优的解。杨时刚等 [9] 对直线方向单组列车编组计划问题通过设置0-1变量建立模型,利用人工神经网络和模拟退火算法求解大量的实例。Yaghini M等 [10] 通过最小化运行商品的成本,以其为目标建立整数规划模型,利用蚁群算法找到信息素最大时所对应的决策变量的值,实现货运编组问题。许红等 [11] 针对技术站单组列车编组以技术站车辆集结消耗、改编消耗整体最小以及技术站改编能力均衡利用为目标函数,构建协同优化的多目标0-1规划模型,提出了基于分块编码的改进型遗传算法的优化方法。左武 [12] 建立了基于技术效益最大化的一体化货物列车编组计划数学模型,设计了单亲遗传算法、双亲遗传算法和双亲自适应遗传算法分别求解同一算例的单组列车编组计划和一体化列车编组计划问题。杜祜康 [13] 为了对大规模整数规划问题的智能算法提供参考,对基于智能算法求解整数规划问题的研究进行了分析和评述。鉴于现有算法的缺陷与不足,讨论了应用智能算法求解整数规划问题未来可能的研究方向。王保华等 [14] 以同一支车流不可拆散、编组去向容量、车站最大编组去向数量、车站改编能力作为约束条件,以车流走行和改编总成本最小作为目标函数,构建车流改编方案优化模型,在此基础上考虑日均车流量的波动,构造车流改编方案随机优化模型,设计基于随机模拟的混合模拟退火算法。马宏朋 [15] 通过考虑大规模路网下编组计划优化问题的复杂性,以货物在途运输成本、货车在车站的改编时间成本以及车站开行方向列车的集结时间成本之和最小为目标构建了适用于实用型路网列车编组计划优化的线性规划模型,利用快速求解的粒子群和拉格朗日松弛组合优化算法求解模型。Barnhart C等 [16] 对铁路编组问题描述为节点上具有最大程度和流动约束的网络设计问题,并提出启发式拉格朗日松弛方法来求解该问题。
已有关于列车编组计划的研究按其优化目标大致可以为两类:优化经济成本或者时间成本。由前文叙述可知,模型以经济成本作为优化目标时,由于和成本相关的关键参数目前没有公认的可靠取值,只能依靠专家经验进行估值。因此使得整体模型的可靠性受到了限制。针对这个问题,本文设计了主要以列车集结时间以及货物中转耗时为优化目标的单组列车编组计划整数规划优化模型,由于使用了标准化技术作业时间参数,大大提高了模型的可靠性。另一方面,大部分研究仅考虑了一般铁路网络上的编组计划问题。由于未利用货物通道本身的特点以及车流特征,将这些模型应用于货运通道上时,会产生算力资源消耗较大且优化效果一般的问题。另外,相关研究中普遍采用的智能算法,存在参数过多,收敛速度慢,运行时间较长,以及优化结果一般等问题。针对上述问题,本文经过分析货运通道上的车流分布特点,设计了两种基于贪婪策略的迭代算法,通过数值实验表明本文给出的算法运算时间较短,且优化效果较好。
1.3. 本文贡献
本文建立货运通道上的单组列车编组计划问题的优化模型,并且设计了两种针对该模型的贪婪优化算法。本文的主要贡献有以下两点:
1) 通过对货运通道本身特点以及货运通道上车流特征的分析,指出对于货运通道上的列车编组计划优化问题,经济成本优化与时间成本优化具有一致性,并由此建立了以列车集结时间以及货物中转时间为主要优化目标的单组列车编组计划优化模型。
2) 针对上述货运通道上的单组列车编组计划优化模型,设计了两种基于贪婪策略的迭代算法,并且通过数值实验说明其拥有更好的优化结果与更快的运算速度。
本文主要内容安排如下:第二节建立了货运通道上的单组列车编组计划模型;第三节针对上述模型设计了两种基于贪婪策略的迭代算法;第四节设计了关于两种贪婪算法以及遗传算法的数值实验;第五节总结了本文研究内容并且指出进一步的研究方向。
2. 模型
2.1. 模型描述
单组列车编组计划问题主要包含两类决策:每个技术站应当建立哪些编组去向,以及每个编组去向应当吸收哪些车流。问题的已知条件主要包括:铁路网络结构,各技术站的集结时间、中转时间参数等。问题的约束条件主要包括:所有车流必须由需求的起点流入,终点流出;同一车流在一个编组站只能编入某一个编组去向当中,即车流不可拆分。问题的优化目标主要包含两个部分:被分入每个编组去向的车辆等待集结成列车的集结时间成本(根据已有研究可知这个成本与车流强度无关 [2] );每个车流在中间站倒换列车时产生的中转时间成本。
2.2. 模型公式
定义G表示铁路逻辑网络图,V为货运通道路网上各技术站的集合,S为所有车流需求的集合。
定义如下参数:
:从i站到j站的车流路径所包含的技术站的集合,不包含始发站和终到站;
:从i站到j站的编组去向吸收的车流量;
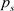 :需求s的原始车流量大小;
:需求s的原始车流量大小;
:从i站到j站的列车的平均编成辆数,本文取该值为55;
:技术站i的列车集结时间;
:沿途中间技术站k节省的时间。
设置如下决策变量:
:当建立从i站到j站的编组去向时,其值为1,否则为0;
:当需求s在运输途中编入从i站到j站的编组去向时,其值为1,否则为0;
根据货物列车编组计划车流不可分割原则,任一车流或者在某站全部改编,或者全部不改编通过技术站,不存在部分改编情况。所以对于任意一支非零技术车流s,存在如下唯一性条件:
。
根据流平衡约束,每一支车流需求必须从需求的起点流入,最终从需求的终点流出,在需求的任意中间点,必须从需求的中间点流入,再从这个中间点流出,分别表示为:
。
从i到j的吸收车流量为:
。
从i站到j站的直达列车沿途节省的时间为:
。
列车节省的站内时间成本包含两部分,一部分为编开直达列车的集结时间成本,第二部分为直达列车在运送过程中沿途站节省的时间成本,目标函数Z为第二部分与第一部分差值的最大值:
。
3. 算法设计
3.1. 贪婪算法一
设S是货运通道路网图G中顶点的有序串构成的集合,是车流需求集合,对任意元素 ,如果两个集合的起点和终点分别相等,则两个需求相等。T是图G中顶点的有序串构成的集合,是所有的编组去向(列车)的集合,对任意从i站到j站的路径 是图G中从i站到j站的最短路。已知需求集合和编组去向的集合确定列车的编组方案,在已知每一个编组方案的基础上求每支车流的所有吸收集合(编挂方法) ,在 中通过计算每个吸收集合可以节省的站内时间成本找到每支车流的最优吸收集合 ,将每支车流的最优吸收集合作为车流的编挂方法求此编组方案的目标值,最终在若干编组方案中找到最优的编组方案 。
基于贪婪策略的迭代算法是根据加入编组去向集合T中的元素来确定当前阶段的所有编组方案,并通过模型的优化目标判定编组方案的优劣,规定同一阶段的列车编组方案只能保留目标值较优的前5000个,最终在最后一阶段的列车编组方案中找最优的列车编组方案。基于贪婪策略的迭代算法设计步骤如下:
第一步 编组方案的确定
通过添加编组去向集合T中的元素确定当前阶段的每一种编组方案,找到当前阶段的所有编组方案的集合。规定第一阶段只有一种编组方案为全部开区段列车即没有编组去向,下一个阶段的所有列车编组方案一部分为上一阶段的编组方案集合,另一部分为将新加的编组去向结合已有的列车编组方案形成新的列车编组方案(第一阶段的编组方案与新添加的编组方案的结合还为新添加的编组方案,其余编组方案之间的结合为对两个编组方案取并集)。例如第一阶段的所有编组方案记为[0],第二阶段新加入编组方向1之后的编组方案为[0]、[1],第三阶段新加入编组方向2之后的编组方案为[0]、[1]、[2]、[1, 2]。
第二步 判断是否满足程序终止条件,确定最优编组方案
判断列车集合T中的所有列车是否全部添加完毕,如果是则根据第三步到五步找最后一阶段的最优编组方案,结束优化。如果没有全部添加完则判断当前阶段的列车编组方案数是否小于5000,如果小于5000则返回第一步,对下一阶段添加新的编组去向,形成新的编组方案,如果不小于5000则计算当前阶段每个编组方案的成本,保留其中目标值较大的前5000个编组方案,成本计算方法执行第三步到第六步。
第三步 根据编组方案确定每个需求的吸收集合
由已知的数据读入列车集合T与需求集合S,在已知当前的编组方案的情况下,求每一个需求s可以挂在哪些编组去向上即s的所有吸收集合 ,需求s只能挂在直达列车的路径不超过需求s的路径的直达列车上,并且需求s的每一个吸收集合中的元素之间没有重复路径,在找需求s的吸收集合时,先判断在当前编组方案中,哪个列车可以摘挂需求s,然后在此基础上找两两之间没有重复路径的需求吸收集合,以此类推,最终找到所有的吸收集合(吸收集合可能是只有一个直达列车,可能是没有重复路径的两个直达列车,也可能是没有重复路径的三个直达列车,以此类推)。
第四步 计算每个需求的最优吸收集合
找到每支需求s的吸收集合之后(每个需求集合s可能有多个吸收集合 ),通过计算每个吸收集合可以节省的站内时间成本找到每支车流的最优吸收集合 。
第五步 编组方案的目标值计算
将当前的编组方案和每个需求的最优吸收集看作决策变量,利用模型当中的目标函数求此编组方案的目标函数值。
第六步 确定下一阶段的编组方案
返回第一步继续确定下一阶段的编组方案,重复以上步骤。
3.2. 贪婪算法二
贪婪策略总是做出在当前看来是最优的选择,在求解货物列车编组计划时每次选取在当前看来加入此编组去向可以使整体的编组方案成本最小的贪婪策略,贪婪策略算法设计步骤如下:
第一步 确定所有可开行的编组去向的集合
根据货运通道路网找到路网上所有可开行的编组去向的集合a,例如 ,可开行3个编组去向,分别为1,2,3。
第二步 确定只开行一趟列车的最优编组方案
在所有可开行的编组去向集合 中,计算只建立一个编组去向时的列车开行成本(根据贪婪策略算法一的最优吸收集合方法和模型的目标函数值计算编组方案的开行成本),找到最小成本对应的编组去向作为 ,删除集合 中的此编组去向。例如分别计算只建立编组去向1的成本,只建立编组去向2的成本,只建立编组去向3的成本,找到成本最小的编组去向为1,因此u = [1],a = [2, 3]。
第三步 确定所有开行方案并计算每个开行方案的目标值
在最优编组去向集合 的基础上添加集合 中的一个编组去向构成新的编组方案,直到将 中的全部编组去向都添加完,形成所有的列车开行方案。利用基于贪婪策略的迭代算法中的方法计算每支车流的最优吸收集合并计算每个列车开行方案的目标值。例如当前的所有开行方案有[1, 2]、[1, 3]。
第四步 判断是否满足程序终止条件
计算所有编组方案的列车开行成本,判断是否所有编组方案的目标值都小于集合u所对应的列车开行成本,如果是则将u作为最优编组方案,结束优化过程。如果不是则找所有编组方案中目标值最大的编组方案作为u,删除集合a中此最优编组方案中的最后一个元素即新添加的编组去向,返回第三步的计算。
3.3. 遗传算法
本文所使用的遗传算法作为两种贪婪策略的对比实验,其编码过程是通过二进制编码来实现的,具体做法为如果开行从i站到j站的编组去向,则其值为1,否则为0,在已知编码方法的基础上随机生成30个个体即0-1矩阵作为遗传算法的初始种群。个体的好坏通过算法的适应度函数来评判,算法的适应度函数取模型的目标函数,目标函数值越大,个体的适应度值越高。在遗传算法进化过程中的选择、交叉、变异过程分别采用轮盘赌输、单点交叉、单点变异的方法,最终将最大迭代次数作为程序终止条件,本文的最大迭代次数取500。
4. 数值实验
4.1. 参数设置
为了验证算法的有效性,本文使用MATLAB对上述算法进行实验,根据已知需求集合,各技术站的参数以及车流路径,建立最优编组方案。铁路货运通道路网规模为10个站点,图中每个圆圈表示一个技术站,两个技术站之间的铁路弧段是有向的,见附录图A1。每个站点的参数,路网中所有需求对应的车流路径以及两两之间的车流需求分别见附录表A1,A2,A3。
4.2. 实验结果
本文进行40组数据实验。从数据1至数据10其车流强度在[5, 35]内;从数据11至数据20其车流强度在[10, 50]内;从数据21至数据30其车流强度在[50, 80]内;从数据31至数据40其车流强度在[80, 120]内。每一组数据分别采用两种贪婪算法以及遗传算法进行求解。实验结果如表1所示。
Table 1. Comparison of experimental results
表1. 实验结果对比
由表1可以看出,在40组实验中,贪婪算法一共计9次获得三种算法中的最佳值;贪婪算法二共计31次获得最佳值;遗传算法共计0次。相比于遗传算法,取两种贪婪算法的最佳目标函数值与遗传算法相比较,优化效果平均提升14%,且两种贪婪算法的运行时间明显短于遗传算法。
5. 结论与展望
货物列车编组计划问题是铁路运输组织工作中的核心内容。本文主要研究了货运通道上的单组列车编组计划优化问题,设计了两种基于贪婪策略的迭代算法。通过算例数值实验表明这两种算法在求解上述问题时速度较快,且优化效果对比遗传算法平均提升14%。如何在货运通道上的编组计划的基础上,更进一步建立整个路网上的列车编组计划,是今后需要继续研究的问题。
基金项目
山西省自然科学基金201801D221193。
文章引用
魏夏琦,焦含笑,梁东岳,张淑蓉,杨卫华. 铁路货运通道上的单组列车编组计划优化算法研究
Research on Optimization Algorithms of Single-Block Train Formation Plan on Railway Corridor[J]. 应用数学进展, 2020, 09(01): 18-29. https://doi.org/10.12677/AAM.2020.91003
参考文献
- 1. 陈崇双, 王慈光, 薛锋, 等. 货物列车编组计划国内外研究综述[J]. 铁道学报, 2012, 34(2): 8-20.
- 2. 胡思继. 铁路行车组织[M]. 第2版. 北京: 中国铁道出版社, 2014: 104-105.
- 3. 严贺祥. 铁路货运通道布局优化的模型和方法研究[D]: [博士学位论文]. 北京: 北京交通大学, 2008.
- 4. 余巧凤, 梁栋. 铁路运输通道现状分析与发展设想[J]. 铁道经济研究, 2009(2): 27-30 + 45.
- 5. Li, Y.H., Wu, S.G. and Peng, Q.Y. (2002) Network Model and Algorithm for Freight Train Marshalling Plan. Journal of Southwest Jiaotong University, 37, 68-71.
- 6. Angel, M. and Javier, S. (2007) Tactical Design of Rail Freight Networks. II: Local Search Methods with Statistical Analysis. European Journal of Operational Research, 94, 43-53.
https://doi.org/10.1016/0377-2217(95)00193-X - 7. Ahuja, R.K., Jha, K.C. and Liu, J. (2007) Solving Real-Life Railroad Blocking Problems. Interfaces, 37, 404-419.
https://doi.org/10.1287/inte.1070.0295 - 8. 林柏梁, 朱松年. 优化编组计划的非线性0-1规划模型及模拟退火算法[J]. 铁道学报, 1994(2): 61-66.
- 9. 杨时刚, 史峰, 李致中. 制定列车编组计划的人工神经网络方法[J]. 铁道科学与工程学报, 2002, 20(3): 79-84.
- 10. Yaghini, M., Foroughi, A. and Nadjari, B. (2011) Solving Railroad Blocking Problem Using Ant Colony Optimization Algorithm. Applied Mathematical Modelling, 35, 5579-5591.
https://doi.org/10.1016/j.apm.2011.05.018 - 11. 许红, 马建军, 龙昭, 等. 技术站单组列车编组方案模型与计算方法的研究[J]. 铁道学报, 2006, 28(3): 12-17.
- 12. 左武. 铁路分组货物列车编组计划的遗传算法研究[D]: [博士学位论文]. 长沙: 中南大学, 2009.
- 13. 杜祜康, 赵英凯. 整数规划问题智能求解算法综述[J]. 计算机应用研究, 2010, 27(2): 408-412.
- 14. 王保华, 何世伟. 铁路车流改编方案随机优化模型及其算法[J]. 中国铁道科学, 2009, 30(5): 104-108.
- 15. 马宏朋. 实用型路网列车编组计划优化模型与算法的研究与实现[D]: [博士学位论文]. 北京: 北京交通大学, 2017.
- 16. Barnhart, C., Jin, H. and Vance, P.H. (2000) Railroad Blocking: A Network Design Application. Operations Research, 48, 603-614.
https://doi.org/10.1287/opre.48.4.603.12416
附录
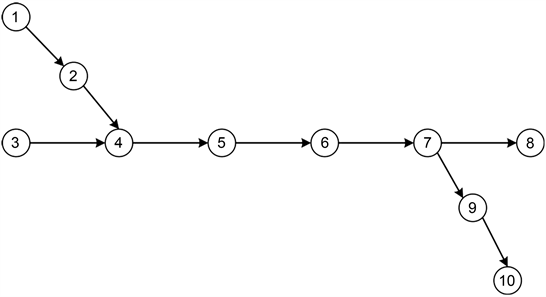
Figure A1. Road network diagram of freight transportation corridor
图A1. 货运通道路网图
Table A1. Parameters of each technical station
表A1. 各技术站参数
Table A2. Traffic flow path for each demand
表A2. 各需求的车流路径










Table A3. Traffic flow transportation demand in road network
表A3. 路网中车流运输需求
NOTES
*通讯作者。
