不完全CI下Wolbachia传播的离散竞争模型 Modeling Wolbachia Propagation underIncomplete Cytoplasmic Incompatibility by Discrete Competition Model

doi:10.12677/AAM.2020.92018

Advances in Applied Mathematics
Vol. 09 No. 02 ( 2020 ), Article ID: 34189 , 13 pages
10.12677/AAM.2020.92018

Modeling Wolbachia Propagation under Incomplete Cytoplasmic Incompatibility by Discrete Competition Model

Yijie Li, Zhiming Guo^*

●How to Cite this Article

School of Mathematics and Information Science, Guangzhou University, Guangzhou Guangdong

Received: Jan. 25^th, 2020; accepted: Feb. 7^th, 2020; published: Feb. 14^th, 2020

ABSTRACT

Dengue fever is one of the most serious mosquito-borne infectious diseases. Using Wolbachia infection mosquitoes to control those diseases is an effective strategy. In this paper, a discrete competition model is established to study the dynamic of Wolbachia propagation under incomplete cytoplasmic incompatibility (CI). We systematically analyze the existing conditions of the equilibrium and global asymptotic behaviors of solutions to this model, then we give the conditions for successful diffusion and the influence of CI strength on the Wolbachia diffusion. Finally, we verify our findings by numerical simulations.

Keywords:Wolbachia, Incomplete CI, Competition, Discrete Model, Stability

不完全CI下Wolbachia传播的离散竞争模型

李艺杰，郭志明^*

广州大学数学与信息科学学院，广东广州

收稿日期：2020年1月25日；录用日期：2020年2月7日；发布日期：2020年2月14日

摘要

登革热是最严重的蚊媒传染病之一，利用Wolbachia氏菌感染野生蚊子来控制蚊媒传染病是一种有效的策略。本文在不完全CI条件下建立了一个离散竞争模型，研究Wolbachia传播动力学行为。我们通过系统地分析平衡点的存在条件和解的全局渐近性态，给出了Wolbachia成功传播的条件以及CI强度对成功传播的影响，最后利用数值模拟验证了主要结论。

关键词 :Wolbachia，不完全CI，竞争，离散模型，稳定性

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

登革热是最为常见的蚊媒传染病之一，主要通过白蚊伊蚊和埃及伊蚊传播 [1]。随着全球气候逐渐变暖以及环境的恶化，适合蚊虫生长的地区范围不断扩大，各种蚊媒传染病在世界范围内许多地区连续爆发，其中登革热就是备受关注的一种。对蚊媒传染病的防治已经成为全人类共同关注的重要公共卫生问题。遗憾的是，目前尚未研制出能够有效地预防蚊媒传染病的疫苗以及抗病毒治疗药物，对蚊媒传染病的防治基本上只能依靠控制蚊子数量来阻断蚊媒传染病的传播。传统的灭蚊方式例如大量喷洒杀虫剂等有很大的局限性，防蚊灭蚊措施亟待改进 [2]。

一种新型高效环保的蚊媒传染病控制方式是利用昆虫体内某些特定的Wolbachia氏菌来阻断蚊媒传染病的传播。特定的Wolbachia氏菌不仅能阻断蚊媒传染病如登革热、疟疾等的传播，还能诱导细胞质不亲和，即CI (cytoplasmic incompatibility)现象。也就是说，感染Wolbachia的雄蚊与未感染的雌蚊交配后所产的卵在胚胎期会全部死亡，不能正常孵化 [3]。2005年，中山大学–密歇根州立大学热带病虫媒控制联合研究中心奚志勇团队从昆虫的体内提取Wolbachia氏菌，然后通过显微注射技术将其注入登革热媒介体内。通过多次试验，最终成功获得稳定携带新型Wolbachia氏菌的蚊株，使得利用Wolbachia氏菌控制蚊媒传染病有了坚实的基础和广阔的前景 [4]。利用Wolbachia氏菌控制蚊媒传染病主要有以下两种策略：1) 种群压制：只释放携带Wolbachia的雄蚊，利用它们与野外雌蚊交配后产生的CI效应来压制野外蚊群的数量 [5]；2) 种群替换：同时释放带Wolbachia的雄蚊和雌蚊，利用Wolbachia的母体垂直传播优势使野外蚊群被携带Wolbachia的蚊群完全替代 [6]。

在利用Wolbachia控制蚊媒病的发展过程中，数学模型的建立与应用具有重要的指导作用。2010年，Farkas等 [7] 建立了一系列数学模型研究Wolbachia的传播动力学，包括在不完全母体传播、不完全CI和具有年龄结构等情形。作者分析了平衡点的稳定性，利用数值模拟估计了平衡点的吸引域，但未给出Wolbachia成功传播的阈值。2014年，郑波等 [8] 建立了一个时滞微分方程模型，给出了精确的感染频率的阈值，同时还发现了感染的雌雄比例为1:5为最佳释放方案。2019年，胡林超等 [9] 建立了一个蚊子繁殖率随机变化的微分方程模型来研究Wolbachia传播动力学，作者获得了感染阈值水平的估计并证明了它不受环境变化的影响，由一条确定的曲线决定。这些模型都具有重要的应用价值。

尽管Wolbachia能诱导CI现象，但由于某些客观因素，小部分受精卵仍旧会成功孵化并产生不携带Wolbachia的蚊子，即为不完全CI。由于不完全CI的存在，即使Wolbachia感染蚊群在竞争过程中占据优势，仍不可避免地会持续产生未感染的蚊子，所以不完全CI将会降低Wolbachia在蚊群中的传播速度，而且CI的强度(指上述受精卵不能孵化的比例)不同，对传播速度的影响程度也不一样 [10]。受上述研究的启发，并注意到野外蚊群数量的观察数据是离散的，本文建立了一个新的离散竞争模型，研究在不完全CI条件下，携带Wolbachia蚊群与野外蚊群的竞争现象，分析Wolbachia成功传播的条件以及CI强度对结果的影响。

2. 模型的建立及其分析

经典的Leslie-Gower离散竞争模型

${\begin{cases} x_{t + 1} = b_{1} \frac{1}{1 + c_{11} x_{t} + c_{12} y_{t}} x_{t}, \\ y_{t + 1} = b_{2} \frac{1}{1 + c_{21} x_{t} + c_{22} y_{t}} y_{t} . \end{cases}$ (1)

该模型具有丰富的动力学性态并且满足竞争排斥原理 [11]。模型中所有系数都是正的， $x_{t}$ 和 $y_{t}$ 分别表示相互竞争的两个种群在时刻t的密度或数量， $b_{1}$ 和 $b_{2}$ 分别表示它们的出生率， $c_{11}$ 和 $c_{22}$ 则分别表示它们的种内竞争系数，而 $c_{12}$ 和 $c_{21}$ 则是种间竞争系数。在此基础上我们建立不完全CI下的Wolbachia传播离散竞争模型。假设 $x_{t}$ 和 $y_{t}$ 分别为感染和未感染Wolbachia的蚊群在时刻t的密度或数量， $b_{1}$ 和 $b_{2}$ 表示它们的出生率。考虑世代重叠的蚊子模型，引入 $d_{1}$ 和 $d_{2}$ 分别表示它们的死亡率，于是它们的幸存率分别为 $1 - d_{1}$ 和 $1 - d_{2}$ ，由于感染Wolbachia的蚊子通常具有适合度劣势 [8]，我们设 $d_{1} > d_{2}$ 。假设q为感染Wolbachia的雄蚊与未感染雌蚊交配后产生受精卵未孵化的比例，则q值即为CI强度(其中 $d_{1}, d_{2}, q \in (0, 1)$ )。由于 $x_{t}$ 和 $y_{t}$ 都表示蚊群数量，所以忽略所有竞争系数之间的差异，让 $c_{11} = c_{12} = c_{21} = c_{22} = α$ ，主要关心竞争对两种群出生率的影响，类似于文献 [7]，在不完全CI下 $y_{t}$ 的出生率变为 $b_{2} [1 - q x_{t} / (x_{t} + y_{t})]$ 。不失一般性，我们有

${\begin{cases} x_{t + 1} = \frac{b_{1} x_{t}}{1 + α (x_{t} + y_{t})} + (1 - d_{1}) x_{t}, \\ y_{t + 1} = \frac{b_{2} y_{t}}{1 + α (x_{t} + y_{t})} (1 - q \frac{x_{t}}{x_{t} + y_{t}}) + (1 - d_{2}) y_{t} . \end{cases}$ (2)

模型中，参数 $b_{1}, b_{2}, d_{1}, d_{2}, α, q$ 都是正实数。

首先考虑模型的非负性和有界性。非负性是显然的，下面证明有界性。

由模型(2)可得

$\begin{array}{l} x_{t + 1} \leq \frac{b_{1}}{α} + (1 - d_{1}) x_{t}, \\ y_{t + 1} \leq \frac{b_{2}}{α} + (1 - d_{2}) y_{t}, \end{array}$

于是由 $d_{1}, d_{2} \in (0, 1)$ ，易得对于任意给定的初值 $x_{0}$ 和 $y_{0}$ ，有

$\underset{t \to \infty}{\lim \sup} x_{t} \leq \frac{b_{1}}{α d_{1}}, \underset{t \to \infty}{\lim \sup} y_{t} \leq \frac{b_{2}}{α d_{2}} .$

因此，模型(2)的所有非负解有界且其正不变集为

$Γ = {(x, y) \in R^{2} | 0 \leq x \leq \frac{b_{1}}{α d_{1}}, 0 \leq y \leq \frac{b_{2}}{α d_{2}}} .$

下面分析模型(2)平衡点的存在性和稳定性。考虑到模型在零点没有定义，为了讨论需要，先定义一个辅助函数

$f (x, y) = {\begin{cases} \frac{b_{2} y}{1 + α (x + y)} (1 - q \frac{x}{x + y}) + (1 - d_{2}) y, (x, y) \neq (0, 0), \\ 0, (x, y) = (0, 0) . \end{cases}$

从而，模型(2)可改写为

${\begin{cases} x_{t + 1} = \frac{b_{1} x_{t}}{1 + α (x_{t} + y_{t})} + (1 - d_{1}) x_{t}, \\ y_{t + 1} = f (x_{t}, y_{t}) . \end{cases}$

此时 $E_{0} (0, 0)$ 可作为模型的平凡平衡点，而其他平衡点满足下面方程组

${\begin{cases} x = \frac{b_{1} x}{1 + α (x + y)} + (1 - d_{1}) x, \\ y = \frac{b_{2} y}{1 + α (x + y)} (1 - q \frac{x}{x + y}) + (1 - d_{2}) y . \end{cases}$ (3)

可以得到模型的两个非负边界平衡点 $E_{1} (\frac{1}{α} (\frac{b_{1}}{d_{1}} - 1), 0)$ 和 $E_{2} (0, \frac{1}{α} (\frac{b_{2}}{d_{2}} - 1))$ ，其存在条件为 $b_{1} > d_{1}$ 和 $b_{2} > d_{2}$ 。另外，系统存在一个正平衡点

$E_{3} (\frac{1}{α q} (\frac{b_{1}}{d_{1}} - 1) (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}}), \frac{1}{α} (\frac{b_{1}}{d_{1}} - 1) [1 - \frac{1}{q} (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})])$

当且仅当条件 $b_{1} > d_{1}$ ， $b_{2} > d_{2}$ 及 $\frac{b_{2}}{d_{2}} > \frac{b_{1}}{d_{1}} > \frac{b_{2}}{d_{2}} (1 - q)$ 成立。下面讨论各平衡点的稳定性。

定理2.1. 对于模型(2)，我们有以下结论。

a) 若 $b_{1} \leq d_{1}, b_{2} \leq d_{2}$ ，则 $E_{0}$ 是全局渐近稳定的；否则， $E_{0}$ 是不稳定的。

b) 若 $b_{1} > d_{1}$ ，则当 $\frac{b_{1}}{d_{1}} > \frac{b_{2}}{d_{2}} (1 - q)$ 时， $E_{1}$ 是局部渐近稳定的；当 $\frac{b_{1}}{d_{1}} < \frac{b_{2}}{d_{2}} (1 - q)$ 时， $E_{1}$ 是一个鞍点。进一步，若 $E_{1}$ 是局部渐近稳定的且 $b_{2} \leq d_{2}$ ，则 $E_{1}$ 是全局渐近稳定的。

c) 若 $b_{2} > d_{2}$ ，则当 $\frac{b_{2}}{d_{2}} > \frac{b_{1}}{d_{1}}$ 时， $E_{2}$ 是局部渐近稳定的；当 $\frac{b_{2}}{d_{2}} < \frac{b_{1}}{d_{1}}$ 时， $E_{2}$ 是一个鞍点。进一步，若 $E_{2}$ 是局部渐近稳定的且 $b_{1} \leq d_{1}$ ，则 $E_{2}$ 是全局渐近稳定的。

证明：模型(2)在平衡点处的Jacobi矩阵为

$J = (\begin{matrix} \frac{b_{1} (1 + α y)}{{[1 + α (x + y)]}^{2}} + 1 - d_{1} & \frac{- α b_{1} x}{{[1 + α (x + y)]}^{2}} \\ \frac{q b_{2} y [α (x^{2} - y^{2}) - y] - α b_{2} y {(x + y)}^{2}}{{[1 + α (x + y)]}^{2} {(x + y)}^{2}} & \frac{q b_{2} x [α (y^{2} - x^{2}) - x] + b_{2} (1 + α x) {(x + y)}^{2}}{{[1 + α (x + y)]}^{2} {(x + y)}^{2}} + 1 - d_{2} \end{matrix}) .$ (4)

从而在平衡点 $E_{1}$ 和 $E_{2}$ 的Jacobi矩阵分别为

$J_{1} = {(\begin{matrix} \frac{d_{1}^{2}}{b_{1}} + 1 - d_{1} & \frac{d_{1}^{2}}{b_{1}} - d_{1} \\ 0 & \frac{b_{2} d_{1} (1 - q)}{b_{1}} + 1 - d_{2} \end{matrix})}_{,}$ (5)

$J_{2} = {(\begin{matrix} \frac{b_{1} d_{2}}{b_{2}} + 1 - d_{1} & 0 \\ \frac{d_{2}^{2}}{b_{2}} - d_{2} (1 + q) & \frac{d_{2}^{2}}{b_{2}} + 1 - d_{2} \end{matrix})}_{,}$ (6)

它们的特征值分别为其对角线上的元素。

a) 若 $b_{1} \leq d_{1}, b_{2} \leq d_{2}$ ，则系统只有一个平凡平衡点 $E_{0}$ 。当 $b_{1} < d_{1}, b_{2} < d_{2}$ 时，由模型(2)可得

$\begin{array}{l} 0 \leq x_{t + 1} \leq (b_{1} - d_{1} + 1) x_{t}, \\ 0 \leq y_{t + 1} \leq (b_{2} - d_{2} + 1) y_{t}, \end{array}$

易得系统的非负解是单调递减的，并且当 $t \to \infty$ 时， $x_{t} \to 0, y_{t} \to 0$ 。因此， $E_{0}$ 是全局渐近稳定的。当 $b_{1} = d_{1}, b_{2} = d_{2}$ 时，由模型(2)可得

$x_{t + 1} = [\frac{b_{1}}{1 + α (x_{t} + y_{t})} + 1 - d_{1}] x_{t},$

$y_{t + 1} = [\frac{b_{2}}{1 + α (x_{t} + y_{t})} (1 - q \frac{x_{t}}{x_{t} + y_{t}}) + 1 - d_{2}] y_{t},$

可知当且仅当 $x_{t} = y_{t} = 0$ 时，对于任意 $t \geq 0$ ，有 $x_{t + 1} = x_{t}, y_{t + 1} = y_{t}$ 。否则，对于任意的 $t \geq 0$ ，有 $0 \leq x_{t + 1} < x_{t}$ ， $0 \leq y_{t + 1} < y_{t}$ 。同理可得 $t \to \infty$ 时， $x_{t} \to 0, y_{t} \to 0$ 。因此， $E_{0}$ 是全局渐近稳定的。当 $b_{1} < d_{1}, b_{2} = d_{2}$ 和 $b_{1} = d_{1}, b_{2} < d_{2}$ 时的情况可以类似的证明，这里不再赘述。综合起来，若 $b_{1} \leq d_{1}, b_{2} \leq d_{2}$ ，则 $E_{0}$ 是全局渐近稳定的。

相反地，若 $b_{1} > d_{1}$ ，则当 $y_{t} = 0$ 时，由模型(2)的第一个式子有

$x_{t + 1} = (\frac{b_{1}}{1 + α x_{t}} + 1 - d_{1}) x_{t},$

易得当且仅当 $x_{t} < \frac{1}{α} (\frac{b_{1}}{d_{1}} - 1)$ 时，有 $\frac{b_{1}}{1 + α x_{t}} + 1 - d_{1} > 1$ 。这表明在X轴上从 $1 < x_{0} < \frac{1}{α} (\frac{b_{1}}{d_{1}} - 1)$ 出发的解将远离 $E_{0}$ ，所以 $E_{0}$ 不稳定。若 $b_{2} > d_{2}$ ，证明类似，这里也不再赘述。

b) $b_{1} > d_{1}$ ，则当 $\frac{b_{1}}{d_{1}} > \frac{b_{2}}{d_{2}} (1 - q)$ 时，由 $J_{1}$ 的所有特征值的绝对值都小于1可知 $E_{1}$ 是局部渐近稳定的；而当 $\frac{b_{1}}{d_{1}} < \frac{b_{2}}{d_{2}} (1 - q)$ 时，由 $J_{1}$ 的一个特征值的绝对值小于1，另一个特征值大于1，可知 $E_{1}$ 是一个鞍点。进一步，若 $E_{1}$ 是局部渐近稳定的且 $b_{2} \leq d_{2}$ ，模型只存在两个平衡点 $E_{0}$ 和 $E_{1}$ ，由a)知此时 $E_{0}$ 不稳定，则根据文献 [12] 中的定理，所有的有界轨线将最终趋于一个平衡点，因此所有轨线只能趋于 $E_{1}$ ，可得 $E_{1}$ 是全局渐近稳定的。

c) 这里的证明与b)类似，所以省略。

接下来我们将讨论当 $b_{1} > d_{1}$ ， $b_{2} > d_{2}$ 时，边界平衡点 $E_{1}$ 、 $E_{2}$ 以及正平衡点 $E_{3}$ 的稳定性态。需要说明的是，当 $\frac{b_{1}}{d_{1}} > \frac{b_{2}}{d_{2}}$ 时，我们说环境有利于感染Wolbachia的蚊群，所以此时感染了Wolbachia的蚊群具有适合度优势。当 $\frac{b_{1}}{d_{1}} < \frac{b_{2}}{d_{2}}$ 时，我们说环境有利于未感染蚊群，所以此时感染Wolbachia的蚊群具有适合度劣势 [8]。由上面讨论可知 $E_{3}$ 的存在条件为 $b_{1} > d_{1}$ ， $b_{2} > d_{2}$ ， $\frac{b_{2}}{d_{2}} > \frac{b_{1}}{d_{1}} > \frac{b_{2}}{d_{2}} (1 - q)$ 。由模型(2)的第一个式子可得垂直等倾线

$y = - x + \frac{1}{α} (\frac{b_{1}}{d_{1}} - 1),$

用 $L_{1}$ 表示，这是一条斜率为−1，截距为 $\frac{1}{α} (\frac{b_{1}}{d_{1}} - 1)$ 的直线段。由模型(2)的第二个式子可得水平等倾线

$α x^{2} + 2 α x y + α y^{2} + [1 + \frac{b_{2}}{d_{2}} (q - 1)] x + (1 - \frac{b_{2}}{d_{2}}) y = 0,$

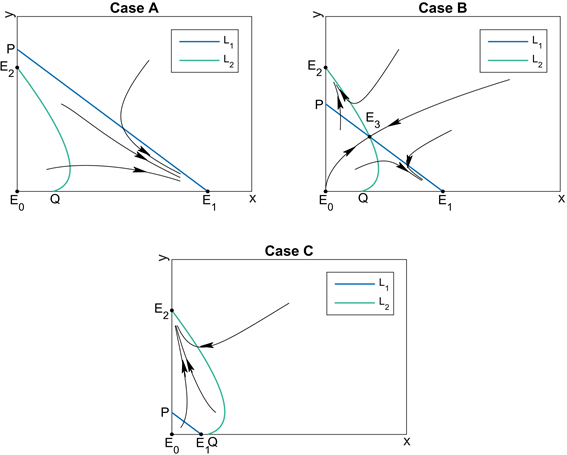
用 $L_{2}$ 表示，这是经过三个不动点 $(0, 0), (0, \frac{1}{α} (\frac{b_{2}}{d_{2}} - 1)), (\frac{1}{α} [\frac{b_{2}}{d_{2}} (1 - q) - 1], 0)$ 的抛物线，见图1。

Figure 1. The three possible cases of L₁and L₂

图1. L₁和L₂的三种情况

Case A的条件为

$b_{1} > d_{1}, b_{2} > d_{2}, \frac{b_{1}}{d_{1}} > \frac{b_{2}}{d_{2}} .$

此时存在三个平衡点 $E_{0}$ ， $E_{1}$ 和 $E_{2}$ ，而 $E_{3}$ 不存在。此时感染Wolbachia的蚊群具有适合度优势。

Case B的条件为

$b_{1} > d_{1}, b_{2} > d_{2}, \frac{b_{2}}{d_{2}} > \frac{b_{1}}{d_{1}} > \frac{b_{2}}{d_{2}} (1 - q) .$

此时存在四个平衡点 $E_{0}$ ， $E_{1}$ ， $E_{2}$ 和 $E_{3}$ ，其中 $E_{3}$ 为 $L_{1}$ 和 $L_{2}$ 的交点。此时感染Wolbachia的蚊群具有适合度劣势。

Case C的条件为

$b_{1} > d_{1}, b_{2} > d_{2}, \frac{b_{1}}{d_{1}} < \frac{b_{2}}{d_{2}} (1 - q) .$

此时存在三个平衡点 $E_{0}$ ， $E_{1}$ 和 $E_{2}$ ，而 $E_{3}$ 不存在。此时感染Wolbachia的蚊群在适合度方面“极度”劣势。下面的定理给出了这三种情况下的平衡点稳定性结论。

定理2.2. 当 $b_{1} > d_{1}$ ， $b_{2} > d_{2}$ 时，我们有

a) 若 $\frac{b_{1}}{d_{1}} > \frac{b_{2}}{d_{2}}$ ，则 $E_{1}$ 是全局渐近稳定的， $E_{2}$ 是一个鞍点。

b) 若 $\frac{b_{2}}{d_{2}} > \frac{b_{1}}{d_{1}} > \frac{b_{2}}{d_{2}} (1 - q)$ ，则 $E_{1}$ 和 $E_{2}$ 都是局部渐近稳定的， $E_{3}$ 是一个鞍点。

c) 若 $\frac{b_{1}}{d_{1}} < \frac{b_{2}}{d_{2}} (1 - q)$ ，则 $E_{2}$ 是全局渐近稳定的， $E_{1}$ 是一个鞍点。

证明：a) 在此条件下(即Case A)，由 $J_{2}$ (见(6))可知 $E_{2}$ 是一个鞍点，不稳定且它的稳定流形是Y轴。利用稳定流形理论以及Hartman-Grobman定理 [13]，可知没有轨线趋于 $E_{2}$ ，而由文献 [12] 中的定理可知所有轨线将趋于 $E_{1}$ 。另外，由 $J_{1}$ (见(5))可知 $E_{1}$ 的所有特征值的绝对值都小于1，所以 $E_{1}$ 是局部渐近稳定的。综上所述， $E_{1}$ 是全局渐近稳定的。

b) 在此条件下(即Case B)，由 $J_{1}$ 、 $J_{2}$ 可得 $E_{1}$ 和 $E_{2}$ 的所有特征值的绝对值都小于1，所以 $E_{1}$ 和 $E_{2}$ 都是局部渐近稳定的。下面讨论 $E_{3}$ 的稳定性，为了表达方便，记

$E_{3} = (x^{*}, y^{*}) = (\frac{1}{α q} (\frac{b_{1}}{d_{1}} - 1) (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}}), \frac{1}{α} (\frac{b_{1}}{d_{1}} - 1) [1 - \frac{1}{q} (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})]) .$

从而系统(2)在平衡点 $E_{3}$ 的Jacobi矩阵为

$J_{3} = {(\begin{matrix} \frac{d_{1}^{2} (1 + α y^{*})}{b_{1}} + 1 - d_{1} & - \frac{α d_{1}^{2} x^{*}}{b_{1}} \\ \frac{q b_{2} y^{*} [(\frac{b_{1}}{d_{1}} - 1) x^{*} - \frac{b_{1}}{d_{1}} y^{*}] - α b_{2} y^{*} {(x^{*} + y^{*})}^{2}}{{[\frac{b_{1}}{d_{1}} (x^{*} + y^{*})]}^{2}} & \frac{q b_{2} x^{*} [(\frac{b_{1}}{d_{1}} - 1) y^{*} - \frac{b_{1}}{d_{1}} x^{*}] + b_{2} (1 + α x^{*}) {(x^{*} + y^{*})}^{2}}{{[\frac{b_{1}}{d_{1}} (x^{*} + y^{*})]}^{2}} + 1 - d_{2} \end{matrix})}_{\cdot}$

(7)

根据Jury判别准则 [14]，平衡点 $E_{3}$ 是局部渐近稳定的当且仅当Jury条件

$| t r J_{3} | < 1 + \det J_{3} < 2$

成立，其中 $t r J_{3}$ 、 $\det J_{3}$ 分别是 $J_{3}$ 的迹和行列式。上述Jury条件也等价于以下三个不等式

$(1) . 1 + \det J_{3} < 2; (2) . - 1 - \det J_{3} < t r J_{3}; (3) . t r J_{3} < 1 + \det J_{3}$

同时成立。直接计算可得，

$\begin{array}{l} \det J_{3} = (\frac{d_{1}^{2}}{b_{1}} + 1 - d_{1}) \frac{q b_{2} x^{*} [(\frac{b_{1}}{d_{1}} - 1) y^{*} - \frac{b_{1}}{d_{1}} x^{*}] + b_{2} (1 + α x^{*}) {(x^{*} + y^{*})}^{2}}{{[\frac{b_{1}}{d_{1}} (x^{*} + y^{*})]}^{2}} \\ + (1 - d_{2}) \frac{d_{1}^{2} (1 + α y^{*})}{b_{1}} + \frac{d_{1}^{4} [α b_{2} y^{*} (x^{*} + y^{*}) - α q b_{2} x^{*} y^{*}]}{b_{1}^{3} (x^{*} + y^{*})} + (1 - d_{1}) (1 - d_{2}), \end{array}$

$t r J_{3} = \frac{q b_{2} x^{*} [(\frac{b_{1}}{d_{1}} - 1) y^{*} - \frac{b_{1}}{d_{1}} x^{*}] + b_{2} (1 + α x^{*}) {(x^{*} + y^{*})}^{2}}{{[\frac{b_{1}}{d_{1}} (x^{*} + y^{*})]}^{2}} + \frac{d_{1}^{2} (1 + α y^{*})}{b_{1}} + 2 - d_{1} - d_{2} .$

利用上面两个式子，易得不等式(3)等价于

$\begin{array}{l} (\frac{d_{1}^{2}}{b_{1}} - d_{1}) \frac{q b_{2} x^{*} [(\frac{b_{1}}{d_{1}} - 1) y^{*} - \frac{b_{1}}{d_{1}} x^{*}] + b_{2} (1 + α x^{*}) {(x^{*} + y^{*})}^{2}}{{[\frac{b_{1}}{d_{1}} (x^{*} + y^{*})]}^{2}} \\ - \frac{d_{1}^{2} d_{2} (1 + α y^{*})}{b_{1}} + \frac{d_{1}^{4} [α b_{2} y^{*} (x^{*} + y^{*}) - α q b_{2} x^{*} y^{*}]}{b_{1}^{3} (x^{*} + y^{*})} + d_{1} d_{2} > 0. \end{array}$

化简后得

$\begin{array}{l} \frac{q b_{2} (\frac{d_{1}}{b_{1}} - 1) x^{*} [(\frac{b_{1}}{d_{1}} - 1) y^{*} - \frac{b_{1}}{d_{1}} x^{*}]}{{[\frac{b_{1}}{d_{1}} (x^{*} + y^{*})]}^{2}} + \frac{d_{1}^{2} b_{2}}{b_{1}^{2}} (\frac{d_{1}}{b_{1}} - 1) (1 + α x^{*}) \\ + d_{2} [1 - \frac{d_{1}}{b_{1}} (1 + α y^{*})] + \frac{d_{1}^{3} [α b_{2} y^{*} (x^{*} + y^{*}) - α q b_{2} x^{*} y^{*}]}{b_{1}^{3} (x^{*} + y^{*})} > 0, \end{array}$

将 $E_{3} = (x^{*}, y^{*})$ 代入上式，有

$\begin{array}{l} \frac{d_{1}^{2} b_{2}}{b_{1}^{2}} (\frac{d_{1}}{b_{1}} - 1) (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}}) [\frac{b_{1}}{d_{1}} - 1 - \frac{1}{q} (2 \frac{b_{1}}{d_{1}} - 1) (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})] + \frac{d_{1}^{2} b_{2}}{b_{1}^{2}} (\frac{b_{1}}{d_{1}} - 1) [1 - \frac{1}{q} (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})] \\ + \frac{d_{1}^{2} b_{2}}{b_{1}^{2}} (\frac{d_{1}}{b_{1}} - 1) [1 + \frac{1}{q} (\frac{b_{1}}{d_{1}} - 1) (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})] + d_{2} (1 - \frac{d_{1}}{b_{1}} (1 + (\frac{b_{1}}{d_{1}} - 1) [1 - \frac{1}{q} (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})])) \\ = \frac{d_{1} b_{2}}{b_{1}} (\frac{d_{1}}{b_{1}} - 1) ((1 - \frac{b_{1} d_{2}}{b_{2} d_{1}}) [1 - \frac{1}{q} (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})] + \frac{d_{2}}{b_{2}} [1 + \frac{1}{q} (\frac{b_{1}}{d_{1}} - 1) (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})]) + d_{2} \end{array}$

$\begin{array}{l} - \frac{d_{1} d_{2}}{b_{1}} (1 + (\frac{b_{1}}{d_{1}} - 1) [1 - \frac{1}{q} (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})]) + \frac{d_{1}^{2} d_{2}}{b_{1}^{2}} (\frac{b_{1}}{d_{1}} - 1) [1 - \frac{1}{q} (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})] \\ = [\frac{d_{1} b_{2}}{b_{1}} (\frac{d_{1}}{b_{1}} - 1) + \frac{d_{1} d_{2}}{b_{1}} (1 - \frac{d_{1}}{b_{1}})] [1 - \frac{1}{q} (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})] + \frac{d_{1} d_{2}}{b_{1}} (\frac{d_{1}}{b_{1}} - 1) \\ + d_{2} (1 - \frac{d_{1}}{b_{1}}) + \frac{d_{1} d_{2}}{q b_{1}} (\frac{d_{1}}{b_{1}} - 1) (\frac{b_{1}}{d_{1}} - 1) (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}}) \\ = \frac{1}{q} (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}}) [\frac{d_{1} b_{2}}{b_{1}} (1 - \frac{d_{1}}{b_{1}}) + d_{2} (\frac{d_{1}}{b_{1}} - 1)] + [\frac{d_{1} b_{2}}{b_{1}} (\frac{d_{1}}{b_{1}} - 1) + d_{2} (1 - \frac{d_{1}}{b_{1}})] \\ = \frac{1}{q} (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}}) - 1 > 0. \end{array}$

在Case B的条件下相反的不等式成立，所以 $E_{3}$ 不稳定。下证其为鞍点。

不等式(2)等价于

$\begin{array}{l} 4 - 2 d_{2} + d_{1} (2 - d_{2}) [\frac{d_{1} (1 + α y^{*})}{b_{1}} - 1] + \frac{d_{1}^{4} [α b_{2} y^{*} (x^{*} + y^{*}) - α q b_{2} x^{*} y^{*}]}{b_{1}^{3} (x^{*} + y^{*})} \\ + (\frac{d_{1}^{2}}{b_{1}} + 2 - d_{1}) \frac{q b_{2} x^{*} [(\frac{b_{1}}{d_{1}} - 1) y^{*} - \frac{b_{1}}{d_{1}} x^{*}] + b_{2} (1 + α x^{*}) {(x^{*} + y^{*})}^{2}}{{[\frac{b_{1}}{d_{1}} (x^{*} + y^{*})]}^{2}} > 0. \end{array}$

我们将证明上式在Case B的条件下成立。将 $E_{3} = (x^{*}, y^{*})$ 代入上式，可得

$\begin{array}{l} 4 - 2 d_{2} + d_{1} (2 - d_{2}) (\frac{d_{1}}{b_{1}} (1 + (\frac{b_{1}}{d_{1}} - 1) [1 - \frac{1}{q} (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})]) - 1) + \frac{d_{1}^{3} d_{2}}{b_{1}^{2}} (\frac{b_{1}}{d_{1}} - 1) [1 - \frac{1}{q} (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})] \\ + \frac{d_{1}^{2} b_{2}}{b_{1}^{2}} (\frac{d_{1}^{2}}{b_{1}} + 2 - d_{1}) [1 + (1 + \frac{1}{q}) (\frac{b_{1}}{d_{1}} - 1) (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}}) - \frac{1}{q} (2 \frac{b_{1}}{d_{1}} - 1) {(1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})}^{2}] > 0, \end{array}$

分别证明上式的各部分都大于0。由 $\frac{b_{2}}{d_{2}} > \frac{b_{1}}{d_{1}} > \frac{b_{2}}{d_{2}} (1 - q)$ 和 $q \in (0, 1)$ ，第一部分：

$\begin{array}{l} 4 - 2 d_{2} + d_{1} (2 - d_{2}) (\frac{d_{1}}{b_{1}} (1 + (\frac{b_{1}}{d_{1}} - 1) [1 - \frac{1}{q} (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})]) - 1) \geq 4 - 2 d_{2} + d_{1} (2 - d_{2}) (\frac{d_{1}}{b_{1}} - 1) \\ = (2 - d_{2}) [2 + d_{1} (\frac{d_{1}}{b_{1}} - 1)] > 0 \end{array}$

成立。看第三部分中括号里面的内容：

$\begin{array}{l} 1 + (1 + \frac{1}{q}) (\frac{b_{1}}{d_{1}} - 1) (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}}) - \frac{1}{q} (2 \frac{b_{1}}{d_{1}} - 1) {(1 - \frac{b_{1} d_{2}}{b_{2} d_{1}})}^{2} \\ \geq 1 + [\frac{b_{1}}{d_{1}} (1 + \frac{1}{q}) - (1 + \frac{1}{q})] (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}}) - (2 \frac{b_{1}}{d_{1}} - 1) (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}}) \\ \geq 1 - (1 + \frac{1}{q}) (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}}) + (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}}) \\ = 1 - \frac{1}{q} (1 - \frac{b_{1} d_{2}}{b_{2} d_{1}}) > 0 \end{array}$

也成立，所以第三部分以及剩下的部分也显然成立，因此(2)的等价式在Case B的条件下成立。现在考虑 $J_{3}$ 的特征多项式

$p (λ) = λ^{2} - (t r J_{3}) λ + \det J_{3} .$

因为不等式(3)在Case B的条件下相反的不等式成立，所以 $p (1) = 1 - t r J_{3} + \det J_{3} < 0$ ，而 $P (- 1) = 1 + t r J_{3} + \det J_{3} > 0$ 因为不等式(2)成立。再由 $P (+ \infty) = + \infty$ ，可知， $P (λ)$ 有一个大于1的正根以及一个在区间 $(- 1, 1)$ 之间的根。因此， $E_{3}$ 是一个鞍点。

c) 在此条件下(即Case C)，证明类似于a)，这里我们不再赘述。定理2.2证毕。

定理2.2的结论表明，在感染蚊群有适合度优势的情况，即Case A， $E_{1}$ 是全局渐近稳定的，无论两种蚊群的初值是多少，Wolbachia都能成功扩散到整个蚊群。相反地，感染蚊群在适合度“极度”劣势的情况下，即Case C， $E_{2}$ 是全局渐近稳定的。无论初值取多少，Wolbachia都扩散失败。实际应用中最为合理的是感染蚊群具有适合度劣势的情况，即Case B，此时 $E_{1}$ 和 $E_{2}$ 都是局部渐近稳定的，它们有各自的吸引域。 $E_{3}$ 是一个鞍点，它的稳定流形分开了 $E_{1}$ 和 $E_{2}$ 的吸引域，Wolbachia扩散成功与否取决于两种群的初值。另外，通过分析，在保持两种群出生率和死亡率不变的情况下，若能不断增加CI的强度(即q值)至完全CI (即 $q = 1$ )，Case C将不存在， $E_{2}$ 在任何情况下都不能全局稳定，意味着q值的增加将有利于携带Wolbachia的蚊群持续存活。实际上在Case B的情况下，q值的增加会使得 $E_{1}$ 的吸引域变大， $E_{2}$ 的吸引域变小。

3. 数值模拟

本节我们将利用利用MATLAB来进行数值模拟来验证相应的结论。主要是对定理2.2的三个结论进行模拟验证以及对CI强度改变的影响进行模拟和解释。图像和说明如下。

图2展示了在Case A情况下两种群的数量变化，其中红实线和黑虚线分别表示感染和未感染蚊群(后面的一样)，参数值为： $α = 1, q = 2 / 3, b_{1} = 3, b_{2} = 2, d_{1} = 0.4, d_{2} = 0.3$ ，所给的初值条件为 $(x_{0}, y_{0}) = (1, 1)$ (左上)、 $(x_{0}, y_{0}) = (2, 4)$ (右上)、 $(x_{0}, y_{0}) = (5, 6)$ (下)。结果显示无论初值取多少，Wolbachia感染蚊群将持续存在，未感染蚊群都将灭绝，即竞争的结果为Wolbachia扩散成功，验证了定理2.2中的a)。

图3展示了在Case B情况下两种群的数量变化，参数值为： $α = 1, q = 2 / 3, b_{1} = 2, b_{2} = 2, d_{1} = 0.4, d_{2} = 0.3$ ，所给的初值条件为： $(x_{0}, y_{0}) = (1, 3)$ (左上)、 $(x_{0}, y_{0}) = (3, 6)$ (右上)、 $(x_{0}, y_{0}) = (1, 1)$ (左下)、 $(x_{0}, y_{0}) = (5, 3)$ (右下)。结果显示不同的初值将导致解趋于 $E_{1}$ 或者 $E_{2}$ ，所以 $E_{1}$ 和 $E_{2}$ 都是局部渐近稳定的，而 $E_{3}$ 是一个鞍点。它的稳定流形分开了 $E_{1}$ 和 $E_{2}$ 的吸引域。若解趋于 $E_{1}$ ，如下两图，则意味着Wolbachia感染蚊群将持续存在，未感染蚊群将灭绝，Wolbachia扩散成功。相反地，如上两图，解趋于 $E_{2}$ ，则扩散失败。验证了定理2.2中的b)。

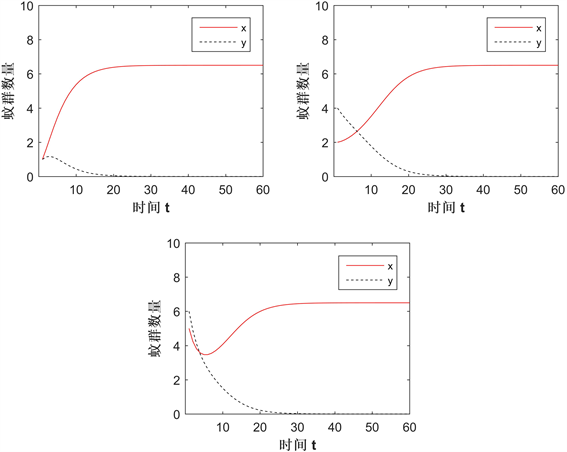
Figure 2. The change in the solution of the system in Case A

图2. Case A情况下系统的解变化

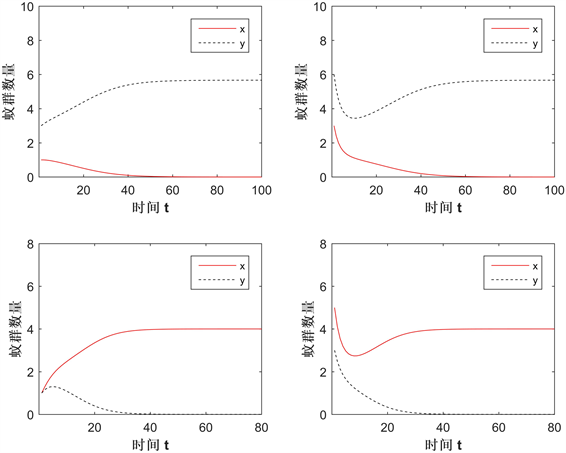
Figure 3. The change in the solution of the system in Case B

图3. Case B情况下系统的解变化

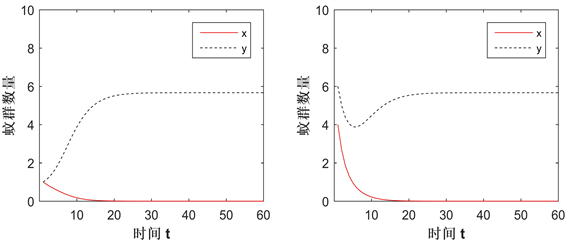
Figure 4. The change in the solution of the system in Case C

图4. Case C情况下系统的解变化

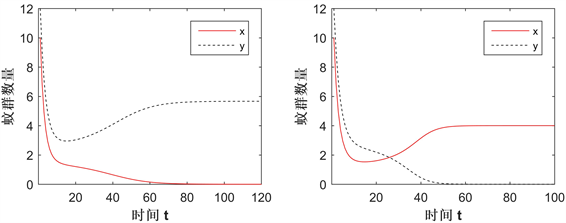
Figure 5. The influence of CI strength changes in Case B

图5. Case B情况下CI强度变化的影响

图4展示了在Case C情况下两种群的数量变化，参数值为： $α = 1$ ， $q = 2 / 3$ ， $b_{1} = 0.8$ ， $b_{2} = 2$ ， $d_{1} = 0.4$ ， $d_{2} = 0.3$ 所给的初值条件为： $(x_{0}, y_{0}) = (1, 1)$ (左)、 $(x_{0}, y_{0}) = (4, 6)$ (右)。结果显示无论初值取多少，Wolbachia感染蚊群将灭绝，未感染蚊群都将持续存在，即竞争的结果为Wolbachia扩散失败。验证了定理2.2中的c)。

图5展示了在Case B情况下，改变CI强度(q值)而导致解趋向的变化。部分参数值为： $α = 1$ ， $b_{1} = 2$ ， $b_{2} = 2$ ， $d_{1} = 0.4$ ， $d_{2} = 0.3$ ，由图像可看到，从初值 $(x_{0}, y_{0}) = (4, 6)$ 出发的解在 $q = 2 / 3$ (左上)时将趋于平衡点 $E_{2}$ ，若增大q值至 $q = 4 / 5$ (右上)，解则变为趋于 $E_{1}$ 。同理，从初值 $(x_{0}, y_{0}) = (10, 12)$ 出发的解在 $q = 2 / 3$ (左下)时趋于 $E_{2}$ ，在 $q = 4 / 5$ (右下)时变为趋于 $E_{1}$ 。意味着CI强度(q值)的增大会增大 $E_{1}$ 的吸引域，减少 $E_{2}$ 的吸引域，即CI强度越大，Wolbachia在蚊群中的传播越容易。

3. 总结

本文从两个种群竞争角度建立了离散模型来分析不完全CI下的Wolbachia传播动力学性态。结果表明：在Wolbachia感染蚊群具有适应度优势的情况下， $E_{1}$ 具有全局渐近稳定性，Wolbachia的成功传播在任何给定的初值条件下都得以保证。在Wolbachia感染蚊群具有适应度“极度”劣势的情况下， $E_{2}$ 具有全局稳定性，Wolbachia传播必然失败。在Wolbachia感染蚊群具有适应度劣势的情况下， $E_{1}$ 和 $E_{2}$ 都是局部渐近稳定的， $E_{3}$ 是一个鞍点，它的稳定流形分开了 $E_{1}$ 和 $E_{2}$ 的吸引域。Wolbachia的传播成功与否将取决于释放的感染蚊群与未感染蚊群的初值，而CI强度的增大将有利于Wolbachia在蚊群中的传播。

基金项目

本文得到国家自然科学基金(11771104)资助。

文章引用

李艺杰,郭志明. 不完全CI下Wolbachia传播的离散竞争模型
Modeling Wolbachia Propagation underIncomplete Cytoplasmic Incompatibility by Discrete Competition Model[J]. 应用数学进展, 2020, 09(02): 153-165. https://doi.org/10.12677/AAM.2020.92018

参考文献

1. Kyle, J.L. and Harris. E. (2008) Global Spread and Persistence of Dengue. Annual Review of Microbiology, 62, 71-92.https://doi.org/10.1146/annurev.micro.62.081307.163005

2. Bardina, S.V., Bunduc, P., Tripathi, S., et al. (2017) Enhancement of Zika Virus Pathogenesis by Preexisting Antiflavivirus Immunity. Science, 356, 175-180. https://doi.org/10.1126/science.aal4365

3. Yen, J.H. and Barr, A.R. (1971) New Hypothesis of the Cause of Cytoplasmic Incompatibility in Culex pipiens L. Nature, 232, 657-658. https://doi.org/10.1038/232657a0

4. Xi, Z.Y., Khoo, C.C., Dobson, S.L., et al. (2005) Wolbachia Establishment and Invasion in an Aedes aegypti Laboratory Population. Science, 310, 326-328. https://doi.org/10.1126/science.1117607

5. Yu, J.S. (2018) Modeling Mos-quitoes Population Suppression Based on Delay Differential Equations. SIAM Journal of Applied Mathematics, 78, 3168-3187. https://doi.org/10.1137/18M1204917

6. Axford, J.K., Ross, P.A., Yeap, H.L., et al. (2016) Fitness of wAlbB Wolbachia Infection in Aedes aegypti: Parameter Estimates in an Outcrossed Background and Potential for Population Invasion. American Journal of Tropical Medicine and Hygiene, 94, 507-516. https://doi.org/10.4269/ajtmh.15-0608

7. Farkas, J.Z. and Hinow, P. (2010) Structured and Unstructured Con-tinuous Models for Wolbachia Infections. Bulletin of Mathematical Biology, 72, 2067-2088. https://doi.org/10.1007/s11538-010-9528-1

8. Zheng, B., Tang, M.X. and Yu, J.S. (2014) Modeling Wolbachia Spread in Mosquitoes through Delay Differential Equations. SIAM Journal of Applied Mathematics, 74, 734-770. https://doi.org/10.1137/13093354X

9. Hu, L.C., Tang, M.X., Wu, Z.D., et al. (2019) The Threshold Infection Level for Wolbachia Invasion in Random Environments. Journal Differential Equations, 266, 4377-4393. https://doi.org/10.1016/j.jde.2018.09.035

10. 邱俊雄, 郭文亮, 郑波. 不完全CI下的Wolbachia动力学行为[J]. 广州大学学报, 2016, 15(6): 34-38.

11. Leslie, P.H. and Gower, J.C. (1958) The Properties of a Stochastic Model for Two Competing Species. Biometrika, 45, 316-330. https://doi.org/10.1093/biomet/45.3-4.316

12. Liu, P.Z. and Elaydi, S.N. (2001) Discrete Competitive and Cooperative Models of Lotka-Volterra Type. Journal of Computational Analysis and Applications, 3, 53-73. https://doi.org/10.1023/A:1011539901001

13. Elaydi, S.N. (1999) An Introduction to Difference Equations. 2nd Edition, Springer, New York. https://doi.org/10.1007/978-1-4757-3110-1

14. Caswell, H. (2001) Matrix Population Models: Construction, Analysis and Interpretation. 2nd Edition, Sinauer Associates, Inc., Sunderland, MA.

期刊菜单