Advances in Applied Mathematics
Vol.
09
No.
05
(
2020
), Article ID:
35420
,
8
pages
10.12677/AAM.2020.95074
An Ensemble Imbalanced Data Classification Algorithm Based on Random k-Rank Nearest Neighbor Rules
Yixin Shen1, Subhash C. Bagui2, Shuangge Ma1*
1College of Mathematics, Taiyuan University of Technology, Jinzhong Shanxi
2Department of Mathematics and Statistics, The University of West Florida, Pensacola FL
Received: Apr. 7th, 2020; accepted: Apr. 29th, 2020; published: May 6th, 2020

ABSTRACT
In this article, a random ensemble k-RNN algorithm called REKRNN is proposed to deal with the imbalanced data classification. The algorithm incorporates the k-rank nearest neighbor classifier into the frame of Bagging algorithm. At the same time, resampling techniques and random feature method are applied to deal with the imbalanced issue. We observe that the proposed method performed remarkably well on different imbalanced dataset. The random ensemble k-RNN algorithm can be considered as a promising tool for imbalanced classification.
Keywords:Imbalanced Data Classification, k-Rank Nearest Neighbor Rule, Bagging, Resampling Techniques

基于随机秩次k近邻规则的不平衡数据 分类算法
沈怡欣1,Subhash C. Bagui2,马双鸽1*
1太原理工大学数学学院,山西 晋中
2西佛罗里达大学数学与统计系,佛罗里达 彭萨科拉

收稿日期:2020年4月7日;录用日期:2020年4月29日;发布日期:2020年5月6日

摘 要
针对不平衡数据分类问题,为提高二分类任务中少数类样本分类准确率低的问题,本文提出一种随机秩次 近邻集成学习算法——REKRNN。该方法将秩次 近邻算法应用于Bagging集成学习框架中,同时采用混合重采样和随机子空间法平衡训练集,增加基学习器差异性。仿真实验证明,该算法在处理不平衡数据分类任务时性能良好。
关键词 :不平衡数据分类,秩次 近邻,集成学习,重采样,随机子空间法

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
分类算法是机器学习的一个重要分支。传统的分类算法大多基于平衡的数据集,即假设不同类别间样例数目相对平衡,并且以总体分类准确率为分类器效能评价指标。然而,在诸多实践中,我们能够获取的数据集中不同类别的样例数往往是不平衡的。例如在病例诊断 [1] 中,多数样例为健康,仅有少数为患病;又如在信用评估 [2] 中,也仅有极少数的样例信用记录不良。当面对不平衡分类任务时,传统的算法会倾向于多数类,假设一个数据集中多数类与少数类的比例为99:1,即使将全部样例均预测为多数类,总体准确率依然可以高达99%。然而在不平衡分类中,更为重要的往往是识别少数类的能力,这使得接近于1的总体分类准确率并无意义。因此,提出针对不平衡数据的有效分类算法尤为重要,这也是近年分类算法研究的一个趋势。
本文从集成学习的角度出发,构建了一个基于Bagging框架的随机秩次k-近邻不平衡数据分类算法(Random Ensemble k-rank nearest neighbor Algorithm, REKRNN)。它将秩次k-近邻分类器(k-rank nearest neighbor,简称k-RNN)应用于集成学习框架中,使k-RNN学习能力强、算法复杂度低的优势,与Bagging的高泛化性能相结合,将重采样和分类算法嵌入推进,最终获得了良好的分类性能。
2. 相关研究
2.1. 不平衡数据分类的集成学习算法
近年来的国内外研究中,提高不平衡数据中少数类分类准确率问题的方法主要分为三个类别:数据层面,算法层面和集成学习。数据层面是指在训练模型之前,对原始数据集进行不同方式的重采样,调整多数类和少数类样本的个数,从而降低不平衡度。例如,通过上采样重复选取少数类样本 [3],或者通过降采样减少多数类样本 [4],来重构数据集使其中不同类别样本数目相对平衡。然而,预处理后用于最终训练分类器的单个数据集,会损失样例特征信息或重复采样多次而造成大量的信息浪费,因此数据层面的方法在不平衡率较高时不适用。算法层面是指针对不平衡数据的特点,提出新的分类算法或者对已有算法做出改变。例如代价敏感学习,通过为不同类别样本设置不同错分代价提高分类准确率。
集成学习是数据和算法的混合方法,它的主要思想是创建一系列弱学习器,再以一定的策略将其结合做出最终决策,利用弱学习器之间的差异性得到更全面的强分类模型。集成学习能够有效地将采样方法和分类算法嵌入推进,是效能更高的不平衡数据分类算法。其中Boosting类通过引入代价敏感学习更新权重,改变多数类和少数类样本的分布,串行生成分类器。它通常基于整个特征空间构建算法,因此整体复杂度较高,不利于高维数据处理。与之相比,Bagging类并行生成基分类器,算法结构更为简单,具有较高的泛化性能 [5] [6]。因此本文提出的REKRNN算法采用Bagging框架,构建以k-RNN为弱学习器的不平衡数据分类算法。
现有的基于Bagging的集成算法中,多数采用决策树作为弱学习器,例如随机森林。近年来,研究者将更多的机器学习算法引入其中,例如神经网络,支持向量机等,使得单个学习器的性能通过集成得到提升 [7]。然而,在特征数较多时,这些算法在学习过程中容易因为复杂度高而产生过拟合现象,使得模型整体泛化性能较差。同时,计算过程时间和资源消耗巨大。
为了降低运算成本,本文首次采用了模型复杂度更低的秩次k近邻算法(k-rank nearest neighbor classifier)作为集成算法的弱学习器。单变量的 -RNN规则首先由Anderson等人于1996年提出,随后Bagui和Pal进一步将之拓展为适用于多变量的分类算法 [8] [9]。与最为经典的k-NN算法相同,它的主要思想是如果一个样本在样本空间中的大多数“邻居”都属于一个类别,那这个样本也属于这个类别 [10]。在分类决策时,只依据这些邻居的类别来做出预测。所不同的是,在寻找最近邻样本时,k-NN基于每两个样本间的距离,而k-RNN基于对各个类别样本混合排序后的次序,即秩次。试验证明,k-RNN在拥有与k-NN相当的分类性能的同时,算法的复杂度更低。
2.2. k-RNN分类器
原始的k-RNN规则适用于单变量总体,即总体中样本仅有一个特征,它规则和主要思想如下:
设 和 是分别来自两个给定总体 和 的训练样本集,测试样例Z可被分类至总体 或 。将X,Y和Z全部样本( 个)按照降序(或升序)排列,得到混合样本的秩次;然后,取Z左边的样本和右边的样本各k个作为秩次最近邻,样例Z的预测类别将由这2k个最近邻中的出现次数较多的类别标记为预测结果。
尽管原始的k-RNN规则有很好的分类能力,但由于“按照降序(或升序)排列”这一概念无法自然地扩展到多变量总体,它只能用于单一特征的总体分类任务。为了将k-RNN规则能够适用于多特征总体分类,并使其在大多数现实问题中得到应用,Bagui扩展了该算法,将Randlest的多维样本排序法引入其中,提出了基于排序的多元k-RNN分类器。该排序法综合了不同总体间的均值和协方差矩阵的差异,更加具有统计学意义。多元k-RNN分类器的主要思想如下:
设
和
是分别来自两个给定总体
和
的训练样本集。其中
,总体均值为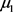 ,协方差矩阵为
;
,总体均值为
,协方差矩阵为
。测试样例
可被分类至总体
或
。基于原始k-RNN规则,测试样例Z在多维样本X,Y和Z中的混合秩次由以下得分函数获得:
,协方差矩阵为
;
,总体均值为
,协方差矩阵为
。测试样例
可被分类至总体
或
。基于原始k-RNN规则,测试样例Z在多维样本X,Y和Z中的混合秩次由以下得分函数获得:
(1)
其中,
表示均值向量
的转置,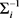 表示协方差矩阵
的逆矩阵。
表示协方差矩阵
的逆矩阵。
在大多数的应用环境中,参数 和 均为未知。Johnson等人证明,可以由它们的无偏估计 和 代替得到得分函数的无偏估计:
(2)
其中,
(3)
(4)
更进一步地,Bagui和Pal利用大数定律证明了 。即得分函数的估计值 依概率收敛到 [8]。
由此可知,得分函数 或者 是一个从 到 ,从p维到1维的映射,它的得分值代表了任一样例在X,Y样本集中的混合秩次。通过得分函数计算X,Y中每个样例的分值,就能够得到混合样本中全部样例的秩次。原始k-RNN规则中排序得到秩次的思想通过得分函数得以解决,使之可以成功应用于多特征分类任务中,依据秩次选择双侧最近邻进行样例的分类预测。
多元k-RNN分类器的训练过程如下表1:
Table 1. k-RNN classifier algorithm
表1. k-RNN分类器训练过程
3. 随机秩次k-近邻集成学习算法
3.1. Bagging算法
Bagging是一种典型的集成学习算法,是当前机器学习算法研究的热点之一,在分类和回归任务中都有广泛的应用和良好的效果。它的实现步骤为:每次从训练集中有放回地抽取n个样本,重复抽取T次;由这T个样本各训练一个弱学习器;由T个弱学习器各对测试样本进行预测,按照投票取众数的方法得到最终预测结果。其中重要的步骤有放回抽样,即为Bootstrap抽样,Bagging名称的来源。它的主要思想是通过弱分类器之间的差异性提高模型泛化性能。针对不平衡数据分类的任务,REKRNN算法对Bagging框架做出如下改进:1) 采用混合重采样法对初始训练集进行采样以获得较为平衡的训练集;2) 引入随机特征子集降低维度和计算复杂度。
3.2. 混合重采样
弱分类器间的差异首先通过重采样得到不同的训练子集获得。在Bagging中,通常由Bootstrap实现重采样过程,即从初始训练集(样本容量为N)中有放回地随机抽取同等数量的样本(N个)形成训练子集。可以证明初始训练集中约63.2%的样本会被选入训练集中,且其中一些样本重复出现。
而针对不平衡数据集,Bootstrap并不会对多数类和少数类样本有任何偏好,依然均衡地进行有放回抽样。因此重采样后的样本子集仍然为不平衡数据集,且当总样本量小或不平衡率很高时,有极大可能Bootstrap子集中没有少数类样本或样本过少影响分类算法的学习。同时,由于REKRNN中弱分类器的算法 -RNN仍然以类别间相对平衡为前提,因此仅仅对少数类获取Bootstrap样本,而对多数类采用降采样随机抽取与少数类相同数目的样本,由此得到少数类数目相对稳定且类别间相对平衡的数据集。
3.3. 随机特征子集
第二个获得弱分类器差异的方法为随机特征子集,即创建若分类器时仅以特征空间的一个子集为分类依据。例如在随机森林中,每棵决策树的节点不是在整个特征空间中进行搜索,而是在一个随机产生的特征子集中选择最优分裂 [11]。与此类似,REKRNN算法在每一个重采样的样本子集上,随机选择不同的特征子集训练弱分类器,保证弱分类器的多样性,增强整体算法的泛化性能。另一方面,随机选择子集可以降低特征维度,在高维数据分类中能够有效提高算法效率。同时,多个子集集成也可以弥补降维带来的潜在精度损失。随机特征子集的选择过程如下表2:
Table 2. Random feature space algorithm
表2. 随机特征子空间算法
3.4. 训练及测试过程
随机秩次k-近邻集成学习算法(REKRNN)将秩次k-近邻分类器k-RNN应用于Bagging集成学习框架中,将k-RNN分类器学习能力强、算法复杂度低的优势,与Bagging算法随机样本空间、随机特征空间分割集成的优势相结合。同时,对该框架加以改进,针对多数类样本采用降采样,针对少数类样本采用Bootstrap重复采样,以获得更加平衡的训练集,有效地提高数据集不平衡时的分类性能。
REKRNN算法的实现主要有四个过程,如图1所示:
1) 按一定比例将数据集划分为测试集和训练集,利用混合重采样法,对少数类样本取Bootstrap样本,多数类进行降采样,从训练集中抽取样本生成r个训练子集;
2) 针对每个训练子集,随机选择将采用的特征数,在特征空间中随机抽取特征子集,生成最终训练样本;
3) 在每个训练样本子集上建立k-RNN弱分类器;
4) 由弱分类器预测测试样本类别,使用“投票法”,将多数弱分类器的预测结果标记为最终分类结果。
4. 实验与结果分析
4.1. 实验数据集
1http://www.keel.es/
为了验证REKRNN算法对于不平衡数据集的分类性能,以及对少数类样本的识别能力,本文选取KEEL1中Abalone9-18数据集进行仿真实验。该数据集含有731个样本的8个特征,其中多数类样例684个,少数类样例仅有42个,不平衡率(多数类/少数类数目)高达16.68,是一个典型的不平衡分类数据集。
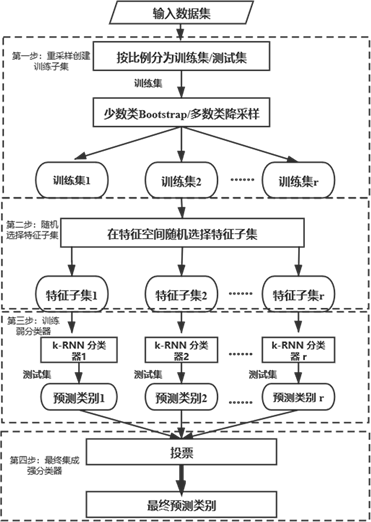
Figure 1. REKRNN algorithm flow chart
图1. REKRNN算法流程图
4.2. 评价指标
定义实验数据集中少数类样本数为P,多数类样本为N,相对应的混淆矩如表3所示:
Table 3. Confusion matrix
表3. 混淆矩阵
依据混淆矩阵,总体精确度(Overall accuracy)为分类正确的样例数占总样例数的比例:
(5)
敏感度(Sensitivity),或查全率(Recall)为被预测为少数类的样例中真正少数类的比例:
(6)
特异性(Specificity),或查准率为实际类别为多数类的样例中也被预测为多数类的比例:
(7)
F值(F-measure),是对敏感度和特异性的折中:
(8)
ROC曲线是对敏感度和特异性的综合图示,AUC (area under ROC curve),即ROC曲线下的面积,经常作为一种不平衡分类的评价指标。
4.3. 实验过程与结果分析
为了验证REKRNN算法的分类性能,以及过程中使用的混合重采样,随即子空间两种技术对于提升学习器k-RNN算法分类性能的效果,分别使用单个基础k-RNN算法,重采样后平衡数据集的k-RNN算法,以及最终形成的REKRNN算法进行仿真实验。同时,以KNN和Adaboost两种模型为参照,比较REKRNN算法的分类效果。
本文使用Python进行仿真实验。k-RNN和KNN中参数k,Adaboost中决策树的数目均由十折交叉验证获得。对于数据集的划分均采用训练集70%,测试集30%的分类比例。以上文提到的五种评价指标为分类效果准则,结果均用百分数表示。实验结果见表4。
Table 4. Experimental output
表4. 实验结果
由上表,我们可以看出,在单个k-RNN分类的基础上,使用混合重采样得到平衡数据集后算法的查全率,F值和AUC分别提高了55.36%,33.51%和20.06%,这表明重采样使得算法对于少数类样本的分类能力大大提升;在此基础上,加入Bagging和随机子空间法后,使用REKRNN模型后查准率,F值和AUC又分别提高了8.9%,4.7%,4.45%,这表明通过集成和随机特征选择又进一步提高了模型的泛化能力。同时,与Adaboost和KNN算法相比,本文提出的REKRNN算法在各个指标下均表现更优,表明此算法在不平衡数据分类中具有良好的表现。
5. 结论与展望
针对不平衡分类任务中少数类样本分类准确率低的问题,本文提出基于随机秩次K近邻规则的不平衡数据分类算法——REKRNN。k-RNN分类能力强,算法复杂度低,Bagging集成框架提高算法整体泛化性能,混合重采样使得子训练集相对平衡,随即子空间算法降低维度的同时增大基学习器差异性。从仿真实验结果来看,这四个元素均对少数类分类准确率的提高有很大贡献,使得算法能够有效识别少数类样例。与两种传统分类算法相比,REKRNN也体现了它在不平衡数据分类中的优势。在下一步的研究中,可以考虑将代价敏感学习引入算法中,通过为少数类样例设置较大错分代价提高其分类准确率,进一步提高算法分类性能。
文章引用
沈怡欣,Subhash C. Bagui,马双鸽. 基于随机秩次k近邻规则的不平衡数据分类算法
An Ensemble Imbalanced Data Classification Algorithm Based on Random k-Rank Nearest Neighbor Rules[J]. 应用数学进展, 2020, 09(05): 622-629. https://doi.org/10.12677/AAM.2020.95074
参考文献
- 1. He, H. and Garcia, E.A. (2009) Learning from Imbalanced Data. IEEE Transactions on Knowledge and Data Engi-neering, 21, 1263-1284. https://doi.org/10.1109/TKDE.2008.239
- 2. Zakaryazad, A. and Duman, E. (2016) A Profit-Driven Artificial Neural Network (ANN) with Applications to Fraud Detection and Direct Marketing. Neuro-computing, 175, 121-131. https://doi.org/10.1016/j.neucom.2015.10.042
- 3. Liu, G., Yang, Y. and Li, B. (2018) Fuzzy Rule-Based Oversampling Technique for Imbalanced and Incomplete Data Learning. Knowledge-Based Systems, 158, 154-174. https://doi.org/10.1016/j.knosys.2018.05.044
- 4. Lin, W.C., Tsai, C.F., Hu, Y.H., et al. (2017) Clustering-Based Undersampling in Class-Imbalanced Data. Information Sciences, 409-410, 17-26. https://doi.org/10.1016/j.ins.2017.05.008
- 5. 沈学华, 周志华, 吴建鑫, 等. Boosting和 Bagging综述[J]. 计算机工程与应用, 2000, 36(12): 31-32, 40.
- 6. 张翔, 周明全, 耿国华, 等. Bagging算法在中文文本分类中的应用[J]. 计算机工程与应用, 2009, 45(5): 135-137, 179.
- 7. 毛国君, 段立娟. 数据挖掘原理与算法[M]. 第3版. 北京: 清华大学出版社, 2016.
- 8. Bagui, S.C., Bagui, S., Pal, K. and Pal, N.R. (2003) Breast Cancer Detection Using Rank Nearest Neighbor Classification Rules. Pattern Recognition, 36, 25-34. https://doi.org/10.1016/S0031-3203(02)00044-4
- 9. Bagui, S.C. and Vaughn, B. (1998) Statistical Classification Based on k-Rank Nearest Neighbor Rule. Statistical Decisions, 16, 181-189. https://doi.org/10.1524/strm.1998.16.2.181
- 10. Gul, A., Perperoglou, A., Khan, Z., et al. (2018) Ensemble of a Subset of KNN Classifiers. Advanced Data Analysis and Classification, 12, 827-840. https://doi.org/10.1007/s11634-015-0227-5
- 11. 李欣海. 随机森林模型在分类与回归分析中的应用[J]. 应用昆虫学报, 2013(4): 1190-1197.
NOTES
*通讯作者。
