International Journal of Mechanics Research
Vol.06 No.04(2017), Article ID:23027,7
pages
10.12677/IJM.2017.64018
Numerical Simulation in Time Domain of Vibration Reduction of Axially Extended Euler Beam
Teng He, Shuo Wang, Bo Fang
Faculty of Aerospace Engineering, Shenyang Aerospace University, Shenyang Liaoning
Received: Nov. 23rd, 2017; accepted: Dec. 7th, 2017; published: Dec. 14th, 2017

ABSTRACT
In this paper, using the Hamilton principle, the nonlinear dynamics equation of an axially moving homogenous and isotropic beam with the additional nonlinear energy sink is derived. The beam, length changes with time, is based on the Euler Bernoulli beam model. Then, transforming the equations to dimensionless ones, using the Galerkin method, the governing equations are truncated. Meanwhile, the nonlinear ordinary differential equation, reflecting the transverse vibration of the telescopic cantilever beam, is obtained. The vibration characteristics of the model in the process of overhang and recovery are analyzed in time domain by numerical calculation method after appropriate nonlinear energy sink parameters were designed. The results show that the nonlinear energy sink has good effect on vibration suppression.
Keywords:Extensible Beam, Isotropic Cantilever Beam, Nonlinear Energy Sink, Nonlinear Dynamics
轴向外伸欧拉梁减振时域数值仿真
贺腾,王朔,方勃
沈阳航空航天大学航空航天工程学部, 辽宁 沈阳
收稿日期:2017年11月23日;录用日期:2017年12月7日;发布日期:2017年12月14日

摘 要
本文基于欧拉–伯努利梁,考虑梁长度随时间变化,利用Hamilton原理,对附加非线性能量阱的轴向可伸缩各向同性矩形截面悬臂梁进行非线性动力学进行建模,得到其偏微分动力学控制方程。然后对控制方程无量纲化后,利用Galerkin方法对控制方程进行了截断,得到可伸缩悬臂梁横向振动的无量纲形式的常微分非线性动力学方程。设计非线性能量阱动力学参数,通过数值方法对模型在外伸和回收过程中的相关振动特性进行了时域分析,结果表明非线性能量阱具有良好的振动抑制效果。
关键词 :可伸缩梁,各向同性悬臂梁,非线性能量阱,非线性动力学

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
时变参数系统是一类航空航天工程领域常见的系统,其动力学参数随时间变化而变化,如航空领域的可变体机翼,大型可展开天线伸缩臂等。其特点是一端固定,一端自由,结构的长度、质量随时间变化。由于现代航空航天科技的快速发展,可变形飞行器的研究受到国内外学者的青睐。前苏联的Bakashaev设计了一架伸缩翼飞机 [1] ,并命名为GK,其伸缩部分外伸长度可达到未伸展时翼展长度的2/3。
李山虎等人 [2] 对轴向运动悬臂梁的独立模态振动控制进行了理论近似解的推导研究。王亮 [3] 等研究了变长度悬臂梁的横向振动控制,提出了两种主动控制方案。Wang [4] 等人利用轴向运动梁模拟时变的变长度航天器天线,考虑了动态系统的空间域随时间变化的运动边值问题,用数值模拟说明了轴向伸长或收缩柔性梁在不同速度下的基本力学特性。随着我国航空航天技术的快速发展,对航空航天仪器的力学环境要求也越来越苛刻,传统减振技术已难以满足要求。非线性能量阱(NES)作为一种新型被动式减振装置得到广泛的关注 [5] [6] 。非线性能量阱其原理是利用非线性刚度连接主结构,使得吸振带宽有所增加,从而提高吸振性能,自2001年靶能量传递现象发现后,非线性能量阱作为一种可实现靶向能量传递的振动被动抑制装置已经进行了大量研究 [7] [8] 。朱玉龙等研究了轴向伸缩复合材料悬臂梁并建立了动力学方程,讨论伸缩梁的动力学特性,推导出伸缩梁保持结构稳定的时间边界,利用微分求积法(DQM)求解伸缩梁固有频率随系统参数的关系 [9] [10] 。
本文将采用Euler梁模型,利用Hamilton原理建立非线性动力学模型,用数值仿真分析轴向运动梁的横向振动,分析对比以梁端附带非线性能量阱进行振动抑制的方案。模型在Euler梁的基础上附着非线性能量阱,对非线性能量阱的减振效果进行研究。可以对航天器的减振应用提供工程参考。
2. 外伸欧拉梁动力学方程
图1所示为一轴向运动的各向同性矩形截面梁,右端自由,末端附有一个非线性能量阱吸振器,左侧可以在 轴方向上自由伸缩。梁的初始长度为 ,厚度为 ,宽度为 。建立如图所示的直角坐标系, 为梁的中面横向位移,即沿 轴正方向位移,梁的瞬时长度 为 ,其中, ,梁的外伸回收速度为 。
建立欧拉梁模型,得到应变与位移的关系式:
(1)

Figure 1. Model diagram
图1. 模型图
本构方程:
(2)
其中 是梁的横向位移, 是正应变, 为弹性模量, 为应变。因此,梁的应变能可以表示为
(3)
动能是
(4)
外力功:
(5)
外力功是作用在梁末端的非线性能量阱上阻尼器和非线性弹簧对梁作用力所作的功,其中k为NES的刚度,c为阻尼。
利用Hamilton原理,可以得到
(6)
将(3)、(4)、(5)式代入(6)得到系统的动力学方程:
(7-1)
(7-2)
引入以下无量纲变量:
代入(7-1)、(7-2)得到系统无量纲动力学方程:
(8-1)
(8-2)
3. 伽辽金离散
为了研究非线性能量阱(NES)对外伸欧拉梁的振动抑制效果,需要对偏微分方程(8)式离散成常微分方程,这一过程引入伽辽金原理将(8)式离散。由于边界为一端固定,一端自由。可以设横向位移的模态函数为:
(9)
其中, ,
则由超越方程 求出。于是可以设横向假设模态为:
(10)
其中 为广义坐标,对(8)式做二阶伽辽金截断,利用三角函数的正交性,得到常
微分形式的非线性动力学方程为:
(11)
4. 时域数值仿真
取各向同性矩形截面梁初始长度 ,宽 ,高 ,密度 ,弹性模量 。非线性能量阱各参数为:质量 ,刚度为 ,阻尼 。采用龙格-库塔法(利用Matlab中ode45代码编写程序)求解方程(11),取无量纲初始条件:
选取无量纲长度 ,梁作自由振动可以得到图2,如图所示在没有非线性能量阱作用时,梁作等幅振动;加持非线性能量阱后有明显的振动抑制效果,振幅在初始阶段显著减小。
图3(a)、图3(b)分别表示选取无量纲长度 和 时梁末端振动情况,在图3(a)中随着时间梁的长度不断增加,可以看出梁末端振幅在不断增大,而梁末端增加非线性能量阱有显著的振动抑制效果,可以有效地减小振幅随长度增加的扩大;图3(b)中随着时间梁的长度不断减小,

Figure 2. oscillogram of the beam end
图2. 梁末端波形图
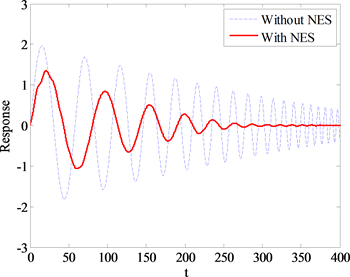 (a)
(a)
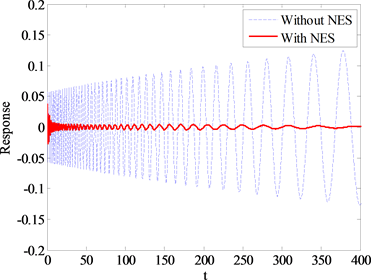 (b)
(b)
Figure 3. (a) oscillogram of the beam end; (b) oscillogram of the beam end
图3. (a) 梁末端波形图;(b) 梁末端波形图
可以看出梁末端振幅在不断减小,而梁末端增加非线性能量阱振幅也随长度不断减小而减小,且振幅小于梁末端未增加非线性能量阱的振幅。
图4(a)表示选取无量纲长度 时梁末端振动情况;图4(b)、图4(c)分别选取无量纲长度 和 时,和 , 梁末端振动情况。与图3(a)相似图4(b)梁的长度随着时间不断增加,可以看出梁末端振幅在不断增大,增加非线性能量阱的梁末端振动抑制效果显著,可以有效地减小梁末端振幅;图4(a)表示选取无量纲长度 时梁末端振动情况,图中随着时间梁的长度不断减小,可以看出梁末端振幅在不断减小,可以看出梁末端振幅先增大后减小,而梁末端增加非线性能量阱时,振幅不断减小且初始间断振动抑制效果明显。图4(c)梁末端振动情况与图4(a)相似。
 (a)
(a)
 (b)
(b)
 (c)
(c)
Figure 4. (a) oscillogram of the beam end; (b) and oscillogram of the beam end; (c) and oscillogram of the beam end
图4. (a) 梁末端波形图;(b) and 梁末端波形图;(c) and 梁末端波形图
5. 结论
本文以可伸缩机翼为实际工程背景,建立可变速运动的欧拉悬臂梁力学模型,模形考虑横向位移与梁长度变化间的关系,引入Hamilton原理对可伸缩机翼进行建模,并附加非线性能量阱,得到其非线性运动控制方程;运用Galerkin方法分别对控制方程做二阶Galerkin截断,得到常微分形式的非线性动力学方程。然后通过龙格—库塔法数值模拟得到以下结论:
1) 在梁外伸过程中,末端的振幅随时间越来越大;在梁回收过程中,末端的振幅随时间越来越小;在外伸过程中梁伸缩到一定长度会发生失稳现象,此时结构力学性能被破坏。
2) 非线性能量阱能有效的抑制梁末端的振动情况。在梁外伸过程中,初始阶段即可有效的抑制振动,并且有效的抑制梁末端振幅随时间的增大;在梁回收过程中,NES可以减小梁末端的振幅。
文章引用
贺 腾,王 朔,方 勃 . 轴向外伸欧拉梁减振时域数值仿真
Numerical Simulation in Time Domain of Vibration Reduction of Axially Extended Euler Beam[J]. 力学研究, 2017, 06(04): 173-179. http://dx.doi.org/10.12677/IJM.2017.64018
参考文献 (References)
- 1. Tabarrok, B., Leech, C.M. and Kim, Y.I. (1974) On the Dynamics of an Axially Moving Beam. Journal of the Franklin Institute, 297, 201-220. https://doi.org/10.1016/0016-0032(74)90104-5
- 2. 李山虎, 杨靖波, 黄清华, 等. 轴向运动悬臂梁的独立模态振动控制-I近似理论分析[J]. 应用力学学报, 2002, 19(1): 35-39.
- 3. 王亮, 陈怀海, 贺旭东, 等. 轴向运动变长度悬臂梁的振动控制[J]. 振动工程学报, 2009, 22(6): 565-570.
- 4. Wang, L.H., Hu, Z.D., Zhong, Z. and Ju, J.W. (2009) Hamiltonian Dynamic Analysis of an Axially Translating Beam Featuring Time-Variant Velocity. Acta Mechanica, 206, 149-161. https://doi.org/10.1007/s00707-008-0104-9
- 5. Bichiou, Y., Hajj, M.R. and Nayfeh, A.H. (2016) Effectiveness of a Nonlinear Energy Sink in the Control of an Aeroelastic System. Nonlinear Dynastic, 86, 2161-2177.
- 6. Zhang, Y.W., Wang, C., Yuan, B., et al. (2017) Integration of Geometrical and Material Nonlinear Energy Sink with Piezoelectric Material Energy Harvester. Shock and Vibration, 2017, Article ID: 1987456. https://doi.org/10.1155/2017/1987456
- 7. 刘天维, 林益明, 王明宇, 等. 航天器振动控制技术进展[J]. 宇航学报, 2008, 29(1): 1-12.
- 8. 张也弛. 非线性能量阱的力学特性与振动抑制效果研究[D]: [博士学位论文]. 哈尔滨: 哈尔滨工业大学, 2012.
- 9. 朱玉龙, 方勃. 考虑剪切变形的复合材料伸缩梁的动力学建模[J]. 工业, 2016, 6(1): 286.
- 10. 朱玉龙. 基于NES的航天器伸缩结构的振动抑制[D]: [硕士学位论文]. 沈阳: 沈阳航空航天大学, 2016.