Journal of Image and Signal Processing
Vol.
10
No.
03
(
2021
), Article ID:
43791
,
14
pages
10.12677/JISP.2021.103013
基于时频图像与迁移学习的雷达信号调制类型识别算法
苑军见,陈世文*,陈蒙,韩啸,杨锦程
战略支援部队信息工程大学,河南 郑州

收稿日期:2021年6月4日;录用日期:2021年6月17日;发布日期:2021年7月9日

摘要
针对雷达信号调制类型识别领域中基于人工提取脉内特征的算法存在的特征提取步骤繁琐、泛化能力弱的缺点,本文提出了一种基于同步压缩短时傅里叶变换(the STFT-based synchrosqueezing transform, FSST)与迁移深度学习的调制类型识别算法。该算法借助深度学习在图像识别领域的优势,使用FSST将信号转换为时频图像并做预处理后作为数据集用于ResNet101网络的训练,同时还借助迁移学习的方法优化了网络的特征提取的能力、加速了模型的训练。考虑到复杂相位编码雷达信号的时频图像较为复杂,具有一定的代表性,本文以多相编码与多时编码信号为研究对象。实验结果表明,本文算法能够有效区分不同调制类型以及相同调制类型不同调制参数的相位编码信号。
关键词
雷达信号,调制类型识别,时频分析,迁移学习
Radar Signal Modulation Type Recognition Algorithm Based on Time-Frequency Image and Transfer Learning
Junjian Yuan, Shiwen Chen*, Mengn Chen, Xiao Han, Jincheng Yang
PLA Strategic Support Force Information Engineering University, Zhengzhou Henan

Received: Jun. 4th, 2021; accepted: Jun. 17th, 2021; published: Jul. 9th, 2021

ABSTRACT
Aiming at the shortcomings of cumbersome feature extraction steps and weak generalization ability of algorithms based on artificially extracting intra-pulse features in the field of radar signal modulation type recognition, this paper proposes a synchronous compression based short-time Fourier transform and transfer deep learning modulation type recognition algorithm. The algorithm uses the advantages of deep learning in the field of image recognition, uses FSST to convert the signal into a time-frequency image and preprocesses it as a data set for the training of the ResNet101 network. At the same time, it also optimizes the feature extraction of the network by means of transfer learning. Ability, accelerate the training of the model, and reduce the training requirements for the size of the data set. Considering that the time-frequency images of complex phase-coded radar signals are more complex and representative, this paper takes polyphase-coded and multi-time-coded signals as the research object. Experimental results show that the proposed algorithm can effectively distinguish phase-encoded signals with different modulation types and the same modulation type with different modulation parameters.
Keywords:Radar Signal, Modulation Type Recognition, Time-Frequency Analysis, Transfer Learning

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
新体制雷达在战场中的使用,使得雷达信号的脉内调制类型日益复杂,不同脉内调制类型的雷达信号的脉内特征存在着或大或小差异,将脉内特征用于雷达信号的分选识别已成为研究的热点。信号的脉内特征可通过人工的方法进行提取,也可通过深度学习技术自动提取。人工方法提取的特征针对性较强,但提取步骤通常较为复杂,同时还存在着泛化能力弱的缺点。与人工提取的特征相比,通过深度学习技术提取的特征泛化能力更强且无需过多的人为干预。目前,深度学习已在雷达信号的分选识别中广泛应用。文献 [1] 通过Choi-Williams分布(CWD)将雷达信号转化为时频图像,对图像做预处理后使用栈式自编码器自动地提取时频图像的特征,最后使用SVM作为分类器对自编码器提取到的特征进行分类。文献 [2] 同样使用CWD获取雷达信号的时频图像,并专门设计了卷积神经网络用于特征的提取与分类,在信噪比−6 dB的条件下,对12种雷达信号的识别率达到了97.58%。文献 [3] 使用深度学习技术对时域混叠雷达信号的识别进行了研究:该文献使用STFT获取雷达信号时频图像,然后利用深度归一化卷积神经网络(deep normalized convolutional neural network, DNCNN)对时频图像进行降噪,最后使用ResNet网络对降噪后的时频图像的特征进行学习与识别。文献 [4] 使用STFT获取雷达信号的时频图像并预处理后分别使用改进的GoogleNet和改进的AlexNet对时频图像进行识别,在低信噪比下,对LFM信号、多相编码信号和多时编码信号的识别获得了较高的正确率。从现有的研究可以发现,目前较为成熟的一套解决方案为:使用时频变换算法获取雷达信号的时频图像并做预处理后送入深度学习网络进行特征的学习与识别。
因此,为对复杂相位编码雷达信号进行识别,本文使用时频分辨率较高的同步压缩短时傅里叶变换(FSST)对信号做时频处理得到时频图像,对图像做预处理后使用ResNet101网络对时频图像进行特征提取与识别,为了优化特征的提取并加快网络的训练,在对网络进行训练时,本文使用了迁移学习技术。
2. 信号模型
雷达信号脉内调制的数学模型可统一表示为:
(1)
式中,A为信号幅度, 为信号载频, 为信号初相,T为信号脉宽。雷达信号各种脉内调制方式均通过改变信号的相位从而对信号做出调制,即对 做出改变。信号的相位可分为两部分: ,其中, ,。对于相位编码信号, 为常数值,主要通过改变 进而改变信号的相位, 的取值与具体的相位编码方式相关。以下分别给出了P1码、P2码、P3码、P4码信号的相位变化规律。
P1码:
(2)
P2码:
(3)
式中, ,相位状态序号 ,编码长度 。对于P2码,M取值为偶数。
P3码:
(4)
P4码:
(5)
式中,相位状态序号 。
T1码、T2码信号的相位是对步进频率波形进行近似产生的。
对于T1编码信号:
(6)
对于T2编码信号:
(7)
式中, ,为步进频率波形的段号;k为步进频率的段数;n为该码序列的相位状态数;INT为向下取整函数; 为取模函数。
T3码、T4码信号的相位是对线性调频波形进行近似产生的。
对于T3编码信号:
(8)
对于T4编码信号:
(9)
式中,n为该码序列的相位状态数; 为调制周期,亦即信号的脉宽; 为调制带宽;INT为取整函数; 为取模函数。
3. 同步压缩短时傅里叶变换
同步压缩短时傅里叶变换是由同步压缩小波变换(synchrosqueezed wavelet transforms, SSWT)发展而来。2011年,Daubechies将小波变换与时频重排技术相结合提出了SSWT算法 [5],该算法的本质是对小波变换的结果进行时频重排,也就是将扩散的能量分布压缩到真实频率附近 [6],与传统时频重排算法不同的是该算法仅在频率方向进行能量的重新分配,可以将其看作时频重排技术的一个特例 [7],这使得该算法支持信号的重构 [8] [9] [10] [11] [12]。FSST是Oberlin与Thakur在SSWT的基础上提出的,与SSWT不同的是,FSST是对信号短时傅里叶变换的结果进行同步压缩 [13] [14]。
下面以解析信号 为例说明FSST的变换过程。任意信号的解析形式都可以表示为:
(10)
首先对信号做短时傅里叶变换(short-time fourier transform, STFT)为了方便计算,文献 [13] 给出了具有调制因子 的STFT计算公式:
(11)
式中, 表示窗函数。如果信号的瞬时幅度和瞬时相位是缓慢变化的,在 的邻域内可以将信号近似表示为 [14]:
(12)
相应地,信号的STFT在 邻域内可以近似为:
(13)
其中, 表示 的傅里叶变换。将 替换成一般的形式:
(14)
从信号STFT的近似表达式中可以看出,能量主要集中在频率 附近。在STFT的基础上,FSST将STFT的系数 按照 的关系进行映射,映射关系式如公式(15)所示,也就是将信号能量沿频率方向重新分配。
滑动窗 是连续的且 的条件下, 的FSST表示为:
(15)
其中 表示 的瞬时频率,由下式计算得到:
(16)
图1给出了映射的示意图,在 时刻STFT时频图上有三个瞬时频率相同的点,即 ,则
(17)

Figure 1. Map Schematic diagram
图1. 映射示意图
图2、图3展示了在信噪比为0 dB、载频 、采样率 的条件下,根据表1设置的信号仿真参数生成信号并使用FSST对信号进行处理得到的信号的时频图(仅展示部分信号)。
 (a) P1_1信号FSST图像
(a) P1_1信号FSST图像
 (b) P2_1信号FSST图像
(b) P2_1信号FSST图像
 (c) P3_1信号FSST图像
(c) P3_1信号FSST图像
 (d) P4_1信号FSST图像
(d) P4_1信号FSST图像
Figure 2. Polyphase coded signal FSST images
图2. 多相编码信号FSST图像
 (a) T1_1信号FSST图像
(a) T1_1信号FSST图像
 (b) T2_1信号FSST图像
(b) T2_1信号FSST图像
 (c) T3_1信号FSST图像
(c) T3_1信号FSST图像
 (d) T4_1信号FSST图像
(d) T4_1信号FSST图像
Figure 3. Multi-time coded signal FSST images
图3. 多时编码信号FSST图像
Table 1. Signal list and simulation parameters
表1. 信号列表与仿真参数
4. 网络模型与迁移学习
4.1. ResNet101网络模型
随着深度学习的发展,研究者通过实验发现网络深度增加后,训练往往会出现退化现象,训练误差不降反而升高。为解决该问题,何恺明等人提出残差神经网络(Residual Net, ResNet) [15],ResNet能够在加深网络结构的同时保证训练误差继续降低,更容易获得数据中的复杂特征,且与普通深度学习网络相比具有更小规模的参数量。构成深度残差神经网络的基础是残差块。与普通卷积神经网络相比,残差块的核心思想是引入跳跃连接结构,将输入直接与输出连接 [16],如图4、图5所示。
假设输入为x,理想输出为 。在普通神经网络结构中,需要通过学习直接拟合出映射 ;而在具有残差结构的网络中,只需要拟合出残差映射 。通过这种跳跃的数据连接,能够使输入更快地向前传播。

Figure 4. Common CNN module
图4. 普通卷积神经网络模块

Figure 5. RseNet module
图5. 残差卷积神经网络模块
本文采用的是深度较深的ResNet101网络结构 [15],该网络一共有5个卷积组。卷积组2~5均由多个“瓶颈”结构的残差连接块构成,网络结构示意图如图6所示。“瓶颈”结构残差块以2个1 × 1的卷积层作为输入和输出层,用以减小和扩大数据维数,中间是一个3 × 3的卷积层,这样可以有效降低参数的复杂度。
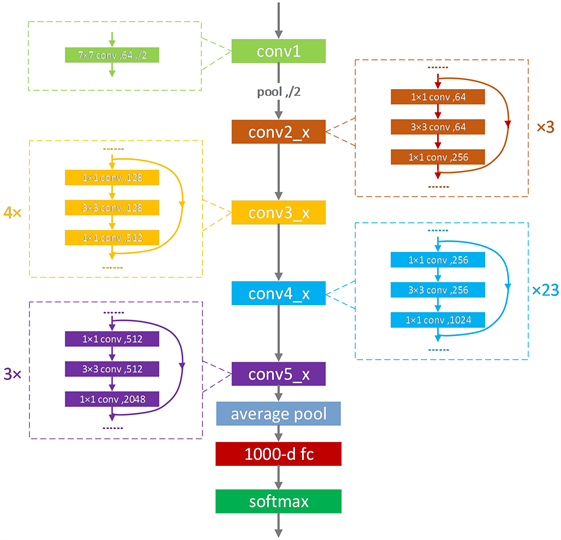 图6. Schematic diagram of ResNet101 network structure
图6. Schematic diagram of ResNet101 network structure
Figure 6. ResNet101网络结构示意图
4.2. 迁移学习
传统的深度学习在对卷积神经网络进行训练时往往需要大量已标注的数据,然而在雷达信号分选识别领域的实际任务中,往往难以获取规模较大的数据集。为解决这一问题,本文使用迁移学习对预训练的网络模型进行参数的微调。迁移学习利用从源域中学习到的知识解决目标域中的问题,其定义如下 [17]:
给定源域 和学习任务 ,一个目标域 和学习任务 ,迁移学习旨在将从 和 中学习到的知识帮助提升 中目标预测函数 的学习。其中 或 ,多数情况下 要大于 的尺寸,即 。
2014年Yosinsk通过实验证明了深度神经网络的可迁移性 [18],Yosinsk发现深度学习网络中各个层的通用性并不相同:较浅层与具体的图像数据集关系不是特别大,浅层的特征基本是通用的,而网络的最后一层则是与选定的数据集及其任务目标紧密相关的。因此在进行迁移学习训练时,往往选择冻结初始层的权重以优化特征的提取及加快训练速度。
5. 算法原理
5.1. 图像预处理
当接收机的工作环境恶劣时,接收到的信号会含有大量噪声,噪声的存在会使得时频图像中存在大量干扰像素,这将会影响下一步的图像训练,同时图像的大小通常不满足网络输入的要求,为此有必要对时频图像进行预处理。本文按照图7所示流程对时频图像进行预处理。

Figure 7. Image preprocessing flow
图7. 图像预处理流程
图8给出了以表1中的信噪比5 dB条件下的P1_1信号为例图像处理实例(为方便观察,部分图片做了反色处理):

Figure 8. Image preprocessing example
图8. 图像预处理实例
5.2. 图像识别流程
图9给出了使用迁移学习对雷达信号进行调制类型识别的流程。原始信号经过FSST变换与时频图像预处理后得到原始数据集,将该数据集按照一定比例划分为训练集、验证集与测试集。预训练模型在开始训练之前首先要替换最终层,其目的是使新的全连接层的输出的数量等于数据集中雷达信号类别的数量。为了加快网络训练速度、防止过拟合还需要冻结部分初始层的权重。
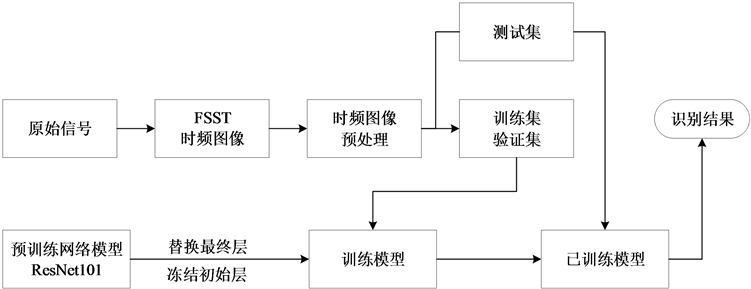
Figure 9. Radar signal modulation type recognition framework
图9. 雷达信号调制类型识别框架
6. 仿真实验与结果分析
6.1. 仿真条件
为了检验本文提出的算法的性能,本节选取P1、P2、P3、P4多相编码信号以及T1、T2、T3、T4多时编码信号进行仿真实验,每种信号设置两种脉内参数,共16类信号。信号载频在500 MHz到600 MHz之间均匀选取,记为 , 代表均匀分布;信号脉宽取值范围设定为 ;信号的采样率 设定为2400 MHz。信号的信噪比范围设置为−10 dB到3 dB,每种类型的信号在每个信噪比下生成200个脉冲,即每类信号分别产生2800个脉冲。上述16类信号详细的脉内参数设置如表1所示。
在训练时,每类信号的数据按照80%、10%、10%的比例划分为训练集、测试集、验证集。训练使用的软件为MATLAB R2020b,并使用单个NVIDIA GeForce RTX 2080 Ti型号GPU对训练进行加速。训练使用到的详细的软硬件环境见表2,训练超参数设置见表3。
Table 2. Experimental environment
表2. 实验环境
Table 3. Training hyperparameter settings
表3. 训练超参数设置
6.2. 实验结果与分析
6.2.1. 识别准确度
实验后,得到如下结果:图10为ResNet101的训练过程,在表2、表3的硬件环境与超参数设置下,5轮训练完成共耗时约两小时,模型的验证正确率在第二轮时已趋于收敛,当训练完全完成时,验证正确率最终为99.87%。
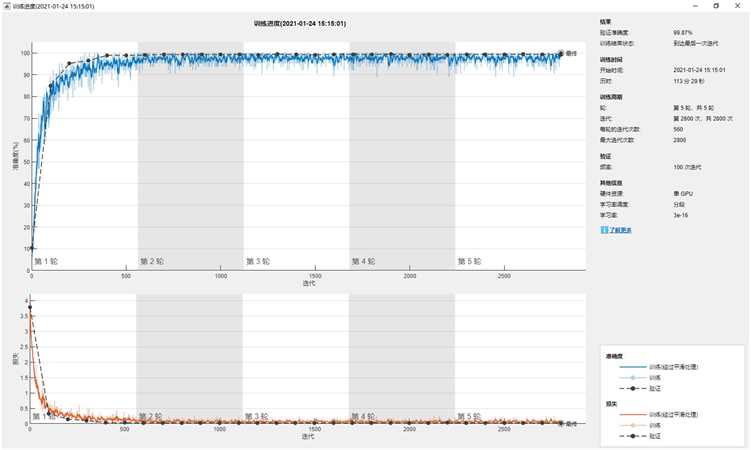
Figure 10. Resnet101 network model training process
图10. Resnet101网络模型训练过程
6.2.2. 网络模型鲁棒性测试
图10反映了随着训练的进行网络模型识别准确率的变化趋势,但没有包含信号识别准确率随信噪比变化的信息,即网络模型的鲁棒性,而这正是我们所关心的。为此本小节使用不同信噪比下的数据对训练好的网络模型进行测试,每种信号在每一个信噪比下使用100张图片。测试的识别结果如图11、图12所示。

Figure 11. Recognition accuracy rate of polyphase coded signal
图11. 多相编码信号识别准确率
图11反映了多相编码信号识别准确率随信噪比变化的情况。可以观察到,各类信号的识别准确率整体上均随信噪比的增高而增高,且P2_1、P2_2、P4_1、P4_2信号的识别准确率整体上要高于P1_1、P1_2、P3_1、P3_2。在信噪比不差于−6 dB时各信号的识别准确率均超过90%,当信噪比不差于−1 dB时,各类信号的识别准确率均超过95%。此外,从图11还可以发现P2_1、P2_2、P4_1这三类信号的准确率在整个信噪比变化范围内识别准确率均超过了90%,P1_1、P3_1信号的识别准确率随信噪比变化最为剧烈。
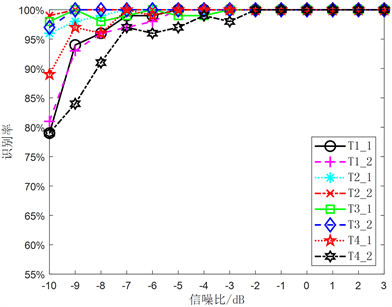
Figure 12. Recognition accuracy rate of multi-time coded signal
图12. 多时编码信号识别准确率
图12反映了多时编码信号识别准确率随信噪比变化的情况。与多相编码相同,多时编码各类信号的识别准确率整体上同样随着信噪比的增高而增高。除T4_2信号外,其余各类信号在信噪比不差于−9 dB时的识别准确率相差不大。在信噪比不差于−8 dB时,各信号的识别准确率均超过90%;当信噪比不差于−7 dB时,各类信号的识别准确率均超过95%。
对比图11与图12可以发现,多相编码信号的识别率整体上要低于多时编码,为了更直观地对比这两种信号的识别正确率,分别绘制它们的平均识别正确率随信噪比变化的曲线,如图13所示。

Figure 13. The average recognition accuracy rate
图13. 信号平均识别正确率
从图13容易发现,多相编码信号的平均识别率在信噪比为[−10 dB, 3 dB]的范围内始终低于多时编码信号。出现上述结果的原因,一是与表1设置的各信号脉内调制参数有关,二是与各类信号的相位编码规律有关。
将测试结果绘制成混淆矩阵,如图14所示。从混淆矩阵可以发现P1_1与P2_2、P1_2与P2_1之间混淆较为严重,其余信号也产生了轻微的混淆。总体来说,多相编码信号的混淆要比多时编码信号严重,识别率最低的信号为P1_2,识别准确率为90.4%,识别率最高的信号为T4_1,信号识别率为99.9%,信号的平均识别率为97.03%。

Figure 14. Robustness test confusion matrix
图14. 鲁棒性测试混淆矩阵
7. 结束语
针对雷达信号调制类型识别领域中基于人工提取脉内特征的算法存在的特征提取步骤繁琐、泛化能力弱的问题,本文提出了使用预训练的ResNet101网络模型进行迁移学习的解决方案。在进行迁移学习之前,首先使用FSST对信号进行时频处理,而后将得到的时频图像进行一系列的预处理得到训练数据集。在进行迁移学习时,首先替换预训练网络模型的最终层并进行一些参数的调整,而后使用准备好的数据集对预训练模型重新进行训练。本文使用了8种共16类相位编码信号进行实验,结果表明,使用预训练的ResNet101网络模型能够较好地完成对相位编码雷达信号的调制识别。
文章引用
苑军见,陈世文,陈 蒙,韩 啸,杨锦程. 基于时频图像与迁移学习的雷达信号调制类型识别算法
Radar Signal Modulation Type Recognition Algorithm Based on Time-Frequency Image and Transfer Learning[J]. 图像与信号处理, 2021, 10(03): 113-126. https://doi.org/10.12677/JISP.2021.103013
参考文献
- 1. 张穆清, 王华力, 倪雪, 等. 基于深度学习与支持向量机的低截获概率雷达信号识别[J]. 科技导报, 2019, 37(4): 69-75.
- 2. Li, D., Yang, R., Li, X., et al. (2020) Radar Signal Modulation Recognition Based on Deep Joint Learning. IEEE Access.
https://doi.org/10.1109/ACCESS.2020.2978875 - 3. Yu, H.H., Yan, X.P., Liu, S.K., et al. (2021) Radar Emitter Multi-Label Recognition Based on Residual Network. Defence Technology.
- 4. Ghadimi, G., Norouzi, Y., Bayderkhani, R., et al. (2020) Deep Learning-Based Approach for Low Probability of Intercept Radar Signal Detection and Classification. Journal of Communications Technology & Electronics, 65, 1179.
https://doi.org/10.1134/S1064226920100034 - 5. Daubechies, I., Lu, J. and Wu, H. (2011) Synchrosqueezed Wavelet Transforms: an Empirical Mode Decomposition-Like Tool. Applied and Computational Harmonic Analysis, 30, 243-261.
https://doi.org/10.1016/j.acha.2010.08.002 - 6. 俞昆, 罗志涛, 李鸿飞, 等. 广义参数化同步压缩变换及其在旋转机械振动信号中的应用[J]. 机械工程学报, 2019, 55(11): 149-159.
- 7. 高威, 李莎. 同步压缩变换及其在机械振动信号处理中的应用[J]. 时代农机, 2017, 44(4): 70-71.
- 8. 张雁. 同步压缩小波变换及其在地震资料处理中的应用研究[D]: [硕士学位论文]. 东营: 中国石油大学(华东), 2018.
- 9. 李振春, 孙苗苗, 王姣, 等. 时间域和频率域二阶同步压缩变换及其在储层识别中的应用[J]. 中国石油大学学报(自然科学版), 2019, 43(3): 36-44.
- 10. 张黎明, 张小栋, 陆竹风, 等. 用于稳态视觉诱发电位特征频率提取的同步压缩短时傅里叶变换方法[J]. 西安交通大学学报, 2017, 51(2): 20-26, 46.
- 11. 薛雷, 曾宏伟, 覃程锦, 等. 采用同步压缩变换和能量熵的机器人加工颤振监测方法[J]. 西安交通大学学报, 2019, 53(8): 24-30, 89.
- 12. 潘宏侠, 张玉学. 基于SST时频图纹理特征的供输弹系统故障诊断[J]. 振动与冲击, 2020, 39(362): 132-137, 175.
- 13. Thakur, G. and Wu, H. (2011) Synchrosqueezing-Based Recovery of Instantaneous Frequency from Nonuniform Samples. Siam Journal on Mathematical Analysis, 43, 2078-2095.
https://doi.org/10.1137/100798818 - 14. Oberlin, T., Meignen, S. and Perrier, V. (2014) The Fourier-Based Synchrosqueezing Transform. IEEE International Conference on Acoustics, Speech and Signal Processing, Florence, 4-9 May 2014, 315-319.
https://doi.org/10.1109/ICASSP.2014.6853609 - 15. He, K., Zhang, X., Ren, S., et al. (2016) Deep Residual Learning for Image Recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, 27-30 June 2016, 770-778.
https://doi.org/10.1109/CVPR.2016.90 - 16. 张驰, 郭媛, 黎明, 等. 人工神经网络模型发展及应用综述[J]. 计算机工程与应用, 2021, 57(11): 1-15.
- 17. Pan, Sinno, Jialin. (2010) A Survey on Transfer Learning. IEEE Transactions on Knowledge & Data Engineering, 22, 1345-1359.
https://doi.org/10.1109/TKDE.2009.191 - 18. Yosinski, J., Clune, J., Bengio, Y., et al. (2014) How Transferable Are Features in Deep Neural Networks? Annual Conference on Neural Information Processing Systems, Montreal, 8-13 December 2014, 3320.
NOTES
*通讯作者。
