Software Engineering and Applications
Vol.
08
No.
05
(
2019
), Article ID:
32511
,
9
pages
10.12677/SEA.2019.85027
Improved K-Means Clustering Algorithm for User Group Discovery and Interest User Recommendation
Dongxiang Zeng, Caifeng Cao, Dongyuan Li
Division of Intelligent Manufacturing, Wuyi University, Jiangmen Guangdong

Received: Sep. 25th, 2019; accepted: Oct. 7th, 2019; published: Oct. 14th, 2019

ABSTRACT
At present, e-commerce websites, learning resource platforms websites and social networking sites generally have the recommendation function for comment things, but not the function of users discovering and recommending users who are interested. In this paper, the FPSHK-means group discovery algorithm was designed by blending a pre-clustering stage on the basis of the K-means clustering algorithm. The pre-clustering stage includes sampling, dimensionality reduction and hierarchical clustering. The FPSHK-means group discovery algorithm is designed to recommend interested users for the users. Through the comparison experiment with the classical K-means clustering algorithm, it is verified that the FPSHK-means group discovery algorithm can find more groups than the classical K-means algorithm. And the result of clustering is closer to the actual distribution of the data object.
Keywords:K-Means Clustering Algorithm, Group Discovery, Users Recommendation
用户群组发现及兴趣用户推荐的改进的K-Means聚类算法
曾东香,曹彩凤,黎冬园
五邑大学智能制造学部,广东 江门

收稿日期:2019年9月25日;录用日期:2019年10月7日;发布日期:2019年10月14日

摘 要
当前,电子商务网站、学习资源平台网站以及社交网站普遍都具备对评价事物的推荐功能,而不具备给用户发现和推荐感兴趣用户的功能。针对此问题,本文在K-means聚类算法的基础上加入包含抽样、降维、层次聚类等过程的预聚类阶段,设计出为用户推荐兴趣用户的FPSHK-means群组发现算法,并通过其与经典K-means聚类算法的对照实验,验证了FPSHK-means群组发现算法能比经典K-means算法发现更多的群组,且聚类结果更贴近数据对象的实际分布情况。
关键词 :K-Means聚类算法,群组发现,用户推荐

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
随着大数据的到来,我们需要一种方式来处理各种类型的海量数据以支持正确的决策和行动。聚类就是获得那些有意义、有实际价值的数据之间的内在分布结构,进而简化海量数据的描述。聚类的目标是把具有相似特性的实物放到一起,即“类内的相似性与类间的排他性” [1] 。到目前为止,聚类研究及其应用领域已经非常广泛,如语音识别、字符识别、图像分割、数据挖掘、时空数据库应用、序列和异类数据分析等领域 [2] 。
本文首先简要介绍了K-means聚类算法的主要过程,然后分析并总结了课题组已发表的SPHK-means聚类算法,提出了一种改进的为用户推荐兴趣用户的FPSHK-means群组发现算法,并与经典的K-means算法进行对比实验。实验结果表明,FPSHK-means群组发现算法的聚类的效果更好、质量更优。
2. 相关知识和工作
2.1. K-Means聚类算法概述
K-means是一种较典型的基于样本间相似性度量的逐点修改迭代的动态聚类算法,属于机器学习中方法中的非监督学习。此算法依据设定的参数k,把n个对象划分到k个簇中,每个簇中心为簇中对象的平均值,使得每一个对象与所属簇的中心具有较高的相似度,而与不同簇的中心相似度较低。K-means算法简单易实现,并且广泛使用,其算法流程图如图1所示。
K-means聚类算法步骤描述如下:
步骤1:输入参数k (类数目)、参数t (准则函数阈值)、距离度量(通常是欧氏距离)和准则函数(通常是误差平方和),并在总体中随机选取k个数据对象作为初始聚类中心 [3] 。
步骤2:分别所有数据对象到k个中心的距离,将总体中的每个数据对象划分到与之距离最小的聚类中心所属的类中。
步骤3:重新计算k个类的中心,每个类的新中心为该类中所有数据对象的均值。
步骤4:计算准则函数,若其值与上一轮迭代相同或少于t,则进行步骤5;否则转至步骤2。
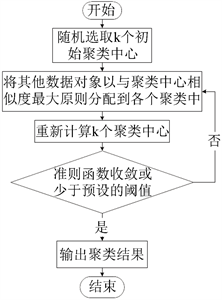
Figure 1. Process of K-means clustering algorithm
图1. K-means聚类算法流程
步骤5:输出各个簇的中心及其成员对象。
K-means聚类算法 [4] - [12] 存在以下缺点。其一,经典的K-means聚类算法对大规模数据集的处理效率低。其二,类数目k难以事先确定,以及初始聚类中心的随机性,这两点使得K-means算法的聚类结果很多时候会陷入局部最优而难以得到全局最优。其三,因为K-means是基于样本间相似度的聚类算法,所以它只能发现球形簇。这些局限都使得经典K-means算法的聚类结果很多时候跟真实的群组分布情况相差较大。
2.2. 群组发现算法SPHK-Means概述
在课题组已发表的论文 [13] 中,提出了一种改进的K-means聚类算法——SPHK-means聚类算法。该算法以弥补本文上一节所述的经典K-means聚类算法的缺点为目标,在进行K-means聚类之前加入两次预聚类。预聚类阶段的步骤包括抽样(Sampling)、主成分分析(Principal Component Analysis)降维和层次聚类(Agglomerative Hierarchical),目的是确定适宜的簇数目k和k个初始聚类中心。在课题组已发表的另一篇论文 [14] 中,使用Movie Lens数据集设计SPHK-means聚类算法与经典K-means聚类算法的对照实验,分别用它们来发现电影类别。在该数据集中,电影实际有19个类别,SPHK-means算法能发现12至15个类别,而经典的K-means算法只能发现2至3个类别,而且SPHK-means算法的F分值比经典K-means算法的F分值高约5%,这说明SPHK-means算法能比经典K-means算法发现更多群组且聚类效果更优。
现对F分值加以说明。假定聚类结果如图2 [15] 所示,Precision和Recall定义如公式(1)和(2),F的定义如公式(3)所示。
(1)
(2)
(3)
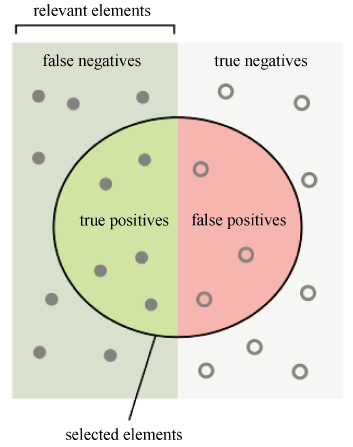
Figure 2. Describe precision and recall
图2. 描述precision和recall
3. FPSHK-Means聚类算法设计
在社交网站中,用户不仅能对具体事物给出评分和书写评论,还能通过浏览其他用户的评分、评论动态,发现感兴趣的其他用户。针对这一应用情景,将设计一种改进的K-means聚类算法,命名为“FPSHK-means”,用于帮助用户发现兴趣群组,并为用户推荐同属一个群组的其他用户。
3.1. 设计思路
SPHK-means聚类算法仍有以下不足之处:
1) SPHK-means算法是在预聚类阶段的每次抽样之后对样本进行降维处理,在真聚类阶段再对数据总体降维。这样的操作顺序可能会因数据的不同而导致样本和总体的主成分分析的系数存在差异,造成样本和总体在降维时的线性变换可能略有不同,进而影响最终聚类结果。
2) SPHK-means算法是直接使用原始用户–物品稀疏评分矩阵R做聚类,对缺失值的处理方法是直接赋0值,这样会忽略用户对未知物品的潜在信息,而这些信息却能够直接影响用户聚类的结果。
针对以上两点做出改进,FPSHK-means聚类算法以奇异值分解(Singular Value Decomposition, SVD)算法计算评分预测值的过程为其数据预处理阶段,用户–物品预测评分矩阵 (而非原始稀疏评分矩阵R)做聚类,并将主成分分析降维安排在其他所有步骤之前。
(而非原始稀疏评分矩阵R)做聚类,并将主成分分析降维安排在其他所有步骤之前。
3.2. 模型设计
设用户总数为U,物品总数为M,则经BC-SVD算法计算填充的用户–物品预测评分矩阵 可表示为:
(4)
其中, 为代表第i个物品的列向量。
FPSHK-means聚类算法的操作流程图如图3所示。

Figure 3. Process of FPSHK-means clustering
图3. FPSHK-means聚类算法流程
FPSHK-means聚类算法步骤如下:
步骤1:为了将代表每位用户u的向量 降至 维( ),对 整体做主成分分析 [16] :
(5)
并使其满足以下三个条件限制 [16] :
1) 对于每个主成分 系数的平方和为1:
(6)
2) 不同的主成分 和 相互独立,即协方差为零:
(7)
3) 所有主成分依其重要程度(方差)呈递减排列,即:
(8)
预测评分矩阵 降维后得到以下矩阵:
(9)
其中, 为预测评分矩阵 中代表用户u的行向量的第 个主成分:
(10)
步骤2:进行第一阶段的预聚类。将所有用户随机分成s组(s由系统预设),每一组成为一份样本,每份样本含有U/s位用户。对s个样本,分别做层次聚类,第i个样本生成的簇的数目为 , ,计算k的均值 和标准差 :
(11)
(12)
令用户群组数的取值范围为 。
步骤3:进行第二阶段的预聚类。逐次抽取一个样本量为s的样本并做层次聚类,直到出现第一个簇数目在 内的样本为止。设该样本的簇数目为 ,簇中心为 。
步骤4:进入真聚类阶段,以 为初始中心,对数据对象总体做K-means聚类,最终得到 个用户群组 ,则为用户u推荐的用户集合为: , 为用户u所属的簇。
4. 实验结果与分析
4.1. 实验数据集与实验环境
算法实验同样使用Movie Lens的Movie Lens Latest Datasets (Small)数据集,其中表movies.csv包含Movie Lens网站对9125部电影的分类标签信息,共19个分类标签,其中前三条记录如表1所示。
Table 1. The top five records of movies
表1. Movies的前五条记录
上表中,“movieId”是Movie Lens数据集对其所包含的电影的编号,“title”是电影的名称,“genres”是电影的分类标签。
由于Movie Lens数据集并没有对671位用户的预定分组,所以对于用户真实的兴趣群组数目只能用电影的预定分类数目估计。
算法实验同样在Ubuntu 16.04操作系统中使用Python 3.6完成。
4.2. 评价指标
聚类属于机器学习中的无监督学习,实验数据集中并没有用户分类的标签数据,无法使用上一章实验的系列评价指标对聚类的结果进行评价。
FPSHK-means算法与经典的K-means算法都属于基于相似度的聚类算法。评价这类算法通常使用误差平方和(Sum of Squared Errors, SSE)作为评价指标。
(13)
其中, 为第i个类簇,i为 的聚类中心。SSE越小,说明聚类结果中各簇的聚合程度越高,聚类的效果越好。
当聚类算法用于群组发现时,希望其能发现贴近数据对象真实分类情况的群组数目和群组结构。若发现的群组数目比数据对象的真实分类数目还多,则该算法对数据对象有比真是分类情况更进一步的细分。
4.3. 实验结果分析
分别以FPSHK-means算法和经典的K-means算法对实验数据集中所有用户做聚类,均用误差平方和SSE作为准则函数且迭代至准则函数收敛为止(相继两次迭代的SSE相同)。重复三次实验,记录每次实验发现的群组数目和算法结束时的SSE,如表2所示。
Table 2. Experimental results comparison of FPSHK-means algorithm and K-means algorithm
表2. FPSHK-means算法与K-means算法实验结果对比
Segaran在他的著作中提到了用于数据可视化的多维缩放技术 [17] ,这个是一种将多维数据集展现在二维平面上的技术。在多维缩放效果图中,数据成员两两间的距离越大,它们在原多维空间中的相似度越小。
应用多维缩放技术,展示FPSHK-means算法和经典K-means算法对实验数据集中671位用户的聚类结果,分别如图4和图5所示,每一位用户用一个点表示。
需要特别说明的是,在此实验中,由于经典的K-means算法需要输入类数目参数k,所以先进行FPSHK-means聚类算法的实验,将FPSHK-means算法发现的群组数目赋给经典K-means算法的参数k。但是随着经典K-means聚类算法的逐次迭代,会陆续出现空组(一次迭代结束后,没有数据对象被归入其中的组称为“空组”)。在此实验中,每出现一个空组就其消除后再进入下一轮迭代(因为就算不将其消除,再往后的迭代过程中也不会有数据对象被划入其中了)。
即便给予经典K-means算法这种事先获得合适k值的“优待”,但由表2可知,FPSHK-means聚类算法依然总是比经典K-means聚类算法发现更多的用户群组(平均多发现约10个群组)。数据集中的电影被预定分19类,但没有用户的预定分组信息,如果以每类电影拥有一个兴趣用户群来估计真实用户群组的话,应该有19个兴趣用户群,希望群组发现算法能发现接近19个或更多的群组。FPSHK-means算法能发现其中的12至14个群组,比经典K-means算法发现的2至3个群组更接近19个兴趣用户群。
而且,FPSHK-means算法结束时的误差平方和SSE总是比经典K-means算法结束时的误差平方和SSE更少,即FPSHK-means算法发现的群组比经典K-means算法发现的群组的组内用户相似性更高,同一群组内的用户的聚拢程度更高。再对比图4和图5可知,FPSHK-means算法不仅比经典K-means算法能发现更多的群组,而且聚类的最终结果也更贴近数据成员在数据集中的自然分布情况,聚类效果更好。
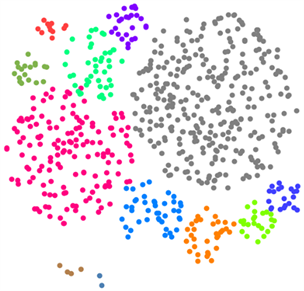
Figure 4. Multidimensional scaling results of FPSHK-means clustering algorithm
图4. FPSHK-means聚类算法的多维缩放效果
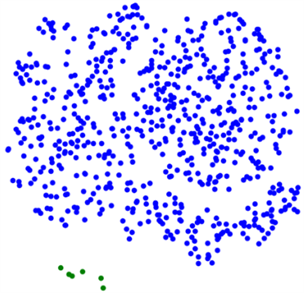
Figure 5. Multidimensional scaling results of K-means clustering algorithm
图5. K-means聚类算法的多维缩放效果
综上所述,本文设计的FPSHK-means群组发现算法能比经典K-means算法发现更多的群组,而且聚类结果更贴近数据对象的实际分布情况。相较于经典K-means算法,FPSHK-means算法的聚类效果更好、聚类结果更优质。
5. 结语
在对K-means算法深入研究的基础上,根据商务网站和社交网站应用场景的需要,设计出为用户推荐兴趣用户的FPSHK-means群组发现算法。阐述了算法的设计思路、模型构建、操作流程和对照实验。下一步工作是将FPSHK-means算法应用到实际应用系统中,已着手设计并实现学习资源推荐系统。并以此为基础,进一步推广与应用。
文章引用
曾东香,曹彩凤,黎冬园. 用户群组发现及兴趣用户推荐的改进的K-Means聚类算法
Improved K-Means Clustering Algorithm for User Group Discovery and Interest User Recommendation[J]. 软件工程与应用, 2019, 08(05): 223-231. https://doi.org/10.12677/SEA.2019.85027
参考文献
- 1. 章永来, 周耀鉴. 聚类算法综述[J]. 计算机应用, 2019, 39(7): 1869-1882.
- 2. 甘月松, 陈秀宏, 陈晓晖. 一种AP算法的改进: M-AP聚类算法[J]. 计算机科学, 2015, 42(1): 232-235+267.
- 3. 王娟. 一种基于遗传算法的K-means聚类算法[J]. 微型机与应用, 2011, 30(20): 71-76.
- 4. Arthur, D. and Vassilvitskii, S. (2007) K-Means++: The Advantages of Careful Seeding. In: Proceedings of the 18th Annual ACM-SIAM Symposium on Discrete Algorithms, Society for Industrial and Applied Mathematics, Philadelphia, PA, 1027-1035.
- 5. Goel, L., Jain, N. and Srivastava, S. (2016) A Novel PSO Based Algorithm to Find Initial Seeds for the K-Means Clustering Algorithm. Communication and Computing Systems Clustering Algorithm. 2016 The International Conference on Communication and Computing Systems, Gurgaon, 9-11 September 2016, 159-163.
- 6. Gu, L. (2017) A Novel Locality Sensitive K-Means Clustering Algorithm Based on Subtractive Clustering. 2016 7th IEEE International Conference on Software Engineering and Service Science, Beijing, 26-28 August 2016, 836-839. https://doi.org/10.1109/ICSESS.2016.7883196
- 7. 谢娟英, 王艳娥. 最小方差优化初始聚类中心的K-Means算法[J]. 计算机工程, 2014, 40(8): 205-211+223.
- 8. 贾瑞玉, 李玉功. 类簇数目和初始中心点自确定的K-Means算法[J]. 计算机工程与应用, 2018, 54(7): 152-158.
- 9. 马福民, 逯瑞强, 张腾飞. 基于局部密度自适应度量的粗糙K-Means聚类算法[J]. 计算机工程与科学, 2018, 40(1): 184-190.
- 10. 丛思安, 王星星. K-Means算法研究综述[J]. 电子技术与软件工程, 2018(17): 155-156.
- 11. 明小红. 基于用户聚类的协同过滤推荐算法研究[D]: [硕士学位论文]. 北京: 北京交通大学, 2017.
- 12. 王千, 王成, 冯振元, 叶金凤. K-Means聚类算法研究综述[J]. 电子设计工程, 2012, 20(7): 21-24.
- 13. Li, D.-Y. and Cao, C.-F. (2017) An Improved K-Means Clustering Algorithm Applicable to Massive High-Dimensional Matrix Datasets. Proceedings of the 2017 International Conference on Information Science and Technology, EDP Sciences, Wuhan, 24-26 March 2017, 269-275.
- 14. Li, D.-Y. and Cao, C.-F. (2017) Discovering Movie Categories Based on SPHK-Means Clustering Algorithm. Proceedings of the 2017 International Conference on Information Science and Technology, EDP Sciences, Wuhan, 24-26 March 2017, 276-283.
- 15. https://en.wikipedia.org/wiki/Precision_and_recall
- 16. Shlens, J. (2014) A Tutorial on Principal Component Analysis. https://arxiv.org/pdf/1404.1100.pdf
- 17. Segaran, T. (2015) Programming Collective Intelligence. Publishing House of Electronics Industry, Beijing, 49-52.
