Service Science and Management
Vol.
09
No.
01
(
2020
), Article ID:
33659
,
9
pages
10.12677/SSEM.2020.91003
Study on Real-Time Adjustment of Customer Service Scheduling Considering Part-Time Staff
Tao Dai, Liuxiao Yang
School of Xu Ri Business Administration, Donghua University, Shanghai

Received: Dec. 9th, 2019; accepted: Dec. 20th, 2019; published: Dec. 27th, 2019

ABSTRACT
With the development of technology, the application of call centers is becoming more and more widespread. At the same time as the scale of enterprises is gradually expanding, the scheduling of customer service has also ushered in new challenges. In the daily operation of the customer service center, the amount of customer consultation will fluctuate on a large scale, resulting in an imbalance between the number of originally planned customer service and the actual manpower requirements, which will cause problems such as excessive customer waiting time or redundant staffing. Aiming at this problem, combined with the current development trend of the part-time market size, a real-time adjustment model considering part-time employment is established with the goal of minimizing costs, and the impact of part-time market structure and part-time job sensitivity on salary is considered. The calculation example shows that the real-time scheduling adjustment model can obtain the scheduling adjustment plan that meets the service level requirements at a lower cost.
Keywords:Part-Time Staff, Customer Service Scheduling, Real-Time Adjustment, Cost Minimization

考虑兼职的客服排班实时调整研究
戴韬,杨柳晓
东华大学,旭日工商管理学院,上海

收稿日期:2019年12月9日;录用日期:2019年12月20日;发布日期:2019年12月27日

摘 要
随着科技的发展,呼叫中心的应用越来越广泛,在企业规模逐渐扩大的同时,客服的排班也迎来了新挑战。在客服中心的日常运营中,客户的咨询量会呈现剧烈波动的现象,导致原计划安排的客服人数与实际人力需求不平衡,从而产生客户等待时间过长或客服人力冗余的问题。本文针对此问题,结合目前兼职市场规模日趋庞大的发展态势,以成本最小化为目标建立了考虑兼职的的实时调整模型,并考虑了兼职市场结构和兼职对薪资的敏感性问题的影响,并设计算例证明此排班实时调整模型能够在较小的成本下满足服务水平要求的排班调整方案。
关键词 :兼职,客服排班,实时调整,成本最小化

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
目前商业竞争日趋激烈,产品同质化问题也愈发严重,服务与销售的关系越来越紧密,客户服务也因此成为了商家的核心竞争力。企业越来越意识到需要通过改善服务来更好地满足用户,以提升企业效益 [1]。呼叫中心作为客户服务的重要渠道之一,被广泛应用于制造业、旅游业、政府、银行等领域 [2]。在企业规模逐渐扩大的同时,客服的排班也迎来了新的挑战。
在客服中心的日常运营中,客户的咨询量往往会出现大规模随机波动的情况,导致原计划安排的客服人数与实际人力需求不平衡,因此需要根据当天收集到的实际数据,对当天剩余排班进行实时调整。但目前大部分的调整都是基于管理人员的经验和直觉 [3]。而近年来,中国的灵活用工市场呈现出日益繁荣的态势,且主要以蓝领和大学生为主 [4]。因此为节约成本和灵活用工,当出现人力不足时,选择调整其他全职员工的班次外,也可以招聘兼职客服来应对咨询高峰期。
目前,国内外对于客服排班实时调整及考虑兼职人员的研究较少。Warburg等 [5] 提出了一种动态航空公司调度模型,能够在预定过程中重新分配机型和出发时间,以满足波动乘客的需求。Easton等 [6] 针对员工缺勤现象,提出了一种缺勤恢复模型,利用延长加班、招聘临时工等恢复策略进行模拟,结果表明在有足够人员储备的情况下,延长加班是一种有效的缺勤恢复方法。Gans等 [7] 探讨了带有排班更新和不带有排班更新的不同排班机制下的成本问题,结果显示前者对运营成本有改善作用。Liao等 [8] 分析了在到达率不确定下有信息更新时的呼叫中心客服排班问题,结果表明在排班过程中考虑可更新的灵活性很有必要。Mehrotra等 [9] 通过建立Overstaffed模型和Understaffed模型,对服务水平和人力成本等受到实时调整的影响而产生变化的问题进行分析,最终平衡三者关系确定排班方案。
本文针对客服中心需求与供给不平衡的问题,结合传统呼叫中心的相关研究,考虑加入兼职建立客服排班实时调整体系,以达到较低的成本与提供更加稳定和优质的服务为目标,为客服中心的排班和实时调整提供理论支持。
2. 考虑兼职的客服排班实时调整模型
2.1. 问题背景
某保险公司人寿保险业务客服中心共240人。因呼叫中心分布式技术的存在,能够在不同地区招聘兼职,由于客服中心所在区域、经济发展状况及兼职市场结构等因素,在排班上以及招聘兼职的难易度也有所区别。
虽然兼职的规模庞大,但兼职与全职客服不同,全职人员是在接受该企业的月薪标准前提下确定入职的,工资不会对其出勤率造成较大影响。而兼职的选择空间大,因此企业招聘兼职时给予的时薪决定了是否有且有足够数量的兼职应聘。
假设兼职的时薪e与应聘的兼职人数q呈图1所示的线性关系。其中k反映的是兼职市场结构,即表示了招聘兼职的难易度。当时薪达到一定值,即EMIN时,才会有兼职应聘,且公司能接受的最高兼职时薪为EMAX,此后兼职数量不再变化。
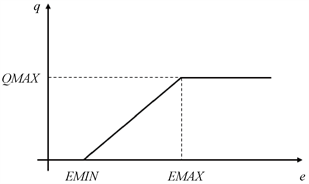
Figure 1. Relationship between hourly pay and number of part-time candidates
图1. 时薪与应聘兼职人数关系图
时薪e与应聘的兼职人数q之间的关系可以表示为:
(2.1)
本文将在此背景下建立实时调整模型进行分析讨论。
2.2. 实时调整模型建立
2.2.1. 模型假设与符号定义
在企业实际运营中会出现部分时段人力不足,而部分时段人力冗余的情况。针对前者,可以采取客服加班或调用其他班组冗余客服,另外,本模型还考虑了雇佣兼职人员的方式,这也是该模型的重点之一。由于呼叫中心分布式技术的存在,可以同时在客服中心分部所在的多个地区招聘兼职,而不同城市的兼职市场结构以及经济发展水平不同,也需要对不同城市的兼职进行分别计算。针对后一种情况,可以将冗余的客服人员分配至其他人力不足的部门继续工作,或安排冗余的客服人员提早下班,或对于原计划该天需要上班但还未到其上班时间的客服人员,取消该天的上班安排。对于后两种,需要对客服人员支付一定的补偿金,即公司需要花费一定的调整成本。在班次实时调整时计算得到的新的人力需求可能会在某些时段大于计划安排的人数,而某些时段小于计划安排的人数,并且会穿插组合。本文假设前一部分时段中,通过实时更新后的客服需求量小于原来安排的客服数量,而后一部分时段中两者的数量则与前一部分时段呈现相反的情况,本文以此组合方式构建实时调整模型。
该模型的构建有如下假设:
(1) 任何班次的客服加班时长不超过8个时段(0.5小时为1个时段);
(2) 其它班组的支援人员,统一的工作时间是16个时段;
(3) 在人力冗余时,若某班次部分客服提前下班时的上班时间不足16个时段,则需在人力短缺时继续上班满16个时段,但不再加班;
(4) 客服加班不超过8个时段,且必须工作16个时段才有机会提前下班;
(5) 对于已确定提前下班客服,当天不再回去工作;
(6) 客户在遇到呼叫占线的情况时等待达到其平均愿意等待时间后即放弃;
(7) 客服平均服务时间比客户平均愿意等待的时间短。
Table 1. Model symbol definition
表1. 模型符号定义
Table 2. Decision variables and definitions
表2. 决策变量及定义
其中, (2.2)
(2.3)
2.2.2. 模型建立
基于以上的问题假设和符号假设,实时调整模型公式如下:
目标函数:
(2.4)
模型约束条件:
(2.5)
(2.6)
(2.7)
(2.8)
(2.9)
(2.10)
(2.11)
(2.12)
(2.13)
(2.14)
(2.15)
(2.16)
其中目标函数第一项是对实时更新后客服人力需求小于计划安排人力时对客服进行调整的成本,后三项则是对需求大于计划人力时的调整成本,最后一项则为兼职成本。约束条件(2.5)表示i班次客服在开始上班时段到其有限的时段范围内满足 时段处于下班状态的人数大于等于在t时段处于离开系统状态的人数。约束(2.6)指在 时段与班次结束后的时段提前下班的客服人数相等。(2.7)指各班次能够提前离开系统的客服人数不能超过该班次上班的人数。(2.8)表示将预计安排提前下班但上班时间不足16个时段的客服调整到从 时段开始继续上班16个时段的客服人数。约束条件(2.9)指i班次客服在t时段加班的人数大于等于 时段加班的客服人数。(2.10)是指 班次客服在其正常下班时段前加班的人数为零。(2.11)指在 时段前上班的班次,至少加班一个时段的客服人数小于等于该班次的总上班人数与该班次提前下班的人数之间的差值。(2.12)表示在 时段后开始上班的客服各个时段的加班人数不超过该班次的总上班人数。(2.13)表示在 时段前所有班次的客服在各个时间段处于离开系统状态的人数不会超过各时段人力冗余值。(2.14)表示在 时段后,调整的客服及兼职人数之和不少于该时段的人力空缺值。约束(2.15)指实际招聘的兼职数小于等于该时段该城市可招到的最大兼职量;(2.16)约束了各参数为正整数或0。
3. 模型应用与求解
排班实时调整模型的输入是计划安排的各时段和班次的客服人力和预估调整后的人力需求。本文假设上述输入值已知,则可通过两者差值来选择相应的调整模型计算得出调整方案。随后综合成本、服务水平等因素做出最终的调整决策。
本文选取了某一天中的48个时段,以该天为例进行讨论分析,图2为该天各时段实际的客服需求与计划安排数量的对比。因此在人力冗余的时段考虑将上班时间不足规定要求的客服调整到人力不足时段,并且在人力不足的时段额外考虑客服加班或招聘兼职客服。
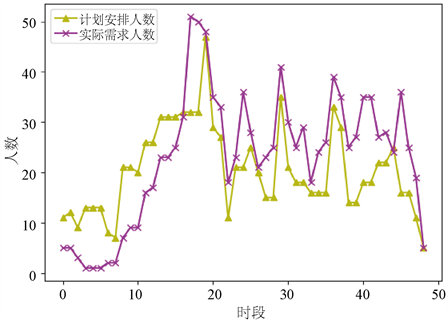
Figure 2. Comparison of actual demand quantity and planned arrangement quantity
图2. 实际需求数量与计划安排数量对比
由于实时调整模型中兼职人数与薪资存在的复杂关系使模型求解速度较慢,因此本文设计了一种新的算法,将求解分为两步进行。
需要明确的是,在客服排班实时调整模型中如遇到安排人力不足时,将采取三种措施,第一是安排客服加班,第二是召集在其他班次上班不足16个时段的客服支援(以下简称移班客服),第三则是招聘兼职客服。首先需要求一个简单模型,该模型认为应聘的兼职数量充足,且不会随着时薪的变化而变化。因此,在模型目标函数中, 将设定为一个确定的值,比较客服加班的时薪和移班的调整成本,取其中较大的一个作为 的值。并且需要去掉混合模型中的约束(2.15)以及约束(2.16)中与 变化有关的约束,如 ,, 等参数都将不存在。通过求解该简单模型,分别求得各个时段的加班客服X、移班客服Z、兼职客服人数Q及相应的调整成本 ,,,其中 与 和 中较大的一个相等。随后,以单独的某个人力不足的时段进行讨论,并且只考虑人力不足的时段。将简单模型求得的兼职人数代入(2.1)式中求得实际招聘到该数量的兼职需要花费的时薪。若计算无解,则表明实际情况下,无法招聘到足够数量的兼职,此时兼职数量应当为QMAX,说明在完全利用了全职客服的基础上仍然无法满足客服的人力需求。若计算得到一个新的时薪值 ,则比较 与 、 之间的大小,若比两者都大,则此时得到最优解,即表明无法以比利用全职客服更优惠的价格招聘到更多数量的兼职来替代全职客服;否则,可将兼职数量Q逐个增加,循环讨论,以替代加班客服或移班客服,从而得到调整成本最低的最优解。具体讨论步骤详见图3。
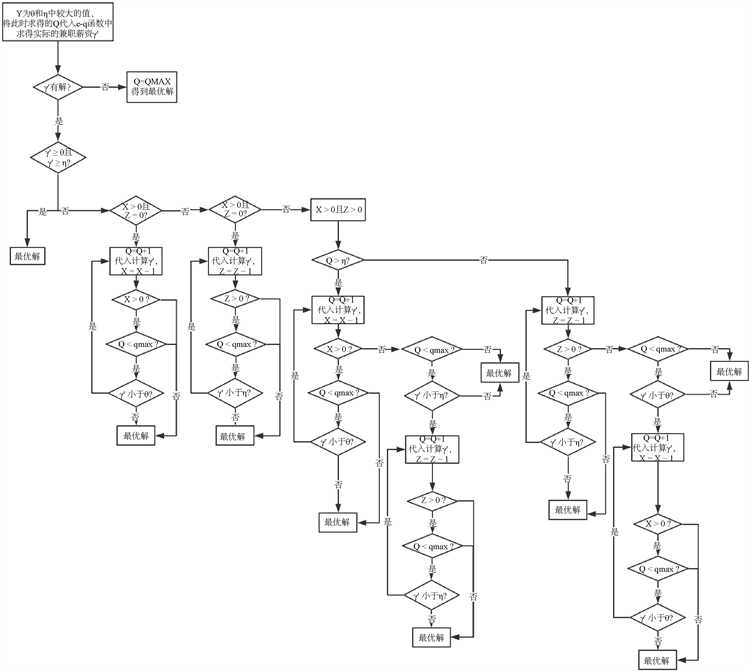
Figure 3. Solution steps for optimal solution of mixed model
图3. 混合模型最优解的求解步骤
本文将以实际算例计算其中一种较为复杂的情况,具体分析该情况下最优解的求解过程。
以某一客服分部为例,该分部所在城市兼职市场结构的相关已知参数值如下:
,,,从而可得 。
此时可招聘兼职数量与薪资关系如下:
(3.1)
另外,设每时段每个加班客服的调整成本为 ,每时段每个移班客服的调整成本为 ,由于 ,因此此时在简单模型中设置每时段每个兼职客服的成本为 ,计算得到如下结果:
该时段安排加班客服数量 ,移班客服数量 ,兼职客服数量 。
将此时的 代入上式中求得 ,说明实际情况下只需14元的成本即可招聘到4名兼职客服,该成本小于安排客服加班或移班的成本,因此可以用兼职替代全职客服。由于 ,因此先尽可能替代成本较大的加班客服,进行第一轮的第一次循环得到:
(1.1)
判断满足 ,进行第二次循环得到:
(1.2)
判断满足 ,进行第三次循环得到:
(1.3)
判断此时不满足 ,说明在兼职薪资还未达到加班成本时已通过招聘兼职将加班客服完全替代。随后比较是否, 满足条件则说明还能够通过继续招聘兼职以替代移班客服,因此进入新一轮的第一次循环得到:
(2.1)
判断满足, 进行第二轮的第二次循环得到:
(2.2)
判断满足 ,进行第二轮的第三次循环得到:
(2.3)
此时判断满足 但 ,表明可招聘兼职数量已达到最高值,无法再通过提高兼职时薪招聘到更多数量的兼职,求解结束,得到该时段的最优解如下:
该时段的调整成本为240元。
通过简单模型求解得到调整成本最优为6147元,再通过后续的算法求解得到该客服中心该天48个时段的最优调整成本共为4793元,节约了1354元,算法求解所需时间在90秒以内。最终,实时调整的客服人力安排与计划安排人力以及实际需求人力如图4所示,可以看到,调整后人力冗余的情况大大减少,并且使得人力不足的时段获得了充足的客服数量,满足了客服中心服务水平的要求。
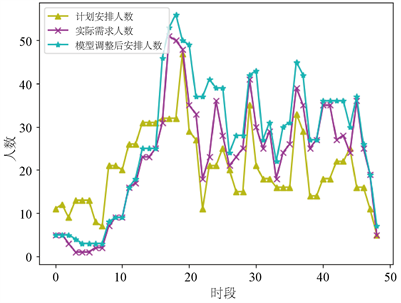
Figure 4. Comparison of the number of adjusted customer service staff
图4. 调整后的客服数量对比图
4. 总结与展望
客服中心在企业运营中起着关键性的作用,因此客服人员的排班计划以及排班表的制定对于企业来说至关重要。本文针对近年来客服中心运营面临精细化管理的问题,提出建立考虑兼职人员的客服排班实时调整模型,通过排班实时调整机制,得到满足客服中心日常运营服务水平目标且成本最小化的排班方案。
本文所提出的研究模型具有较好的创新性、可拓展性和实际应用价值,但由于知识及研究能力的局限,本文讨论的内容中尚有不完善之处,有许多地方值得进一步深入地分析和研究。本文基于LINGO的算法设计较简单,求解速度慢,在日后的工作中应进一步改进算法来提升程序的运行效率和结果的准确性。并且随着电子商务呈现的迅猛发展,在线客服的一对多工作模式与传统呼叫中心客服通过电话与客户进行一对一的服务有较大差异,未来可考虑将本文建立的实时调整模型应用到在线客服的排班中。
致谢
本文感谢国家自然科学基金的支持。
基金项目
国家自然科学基金项目(71872037)。
文章引用
戴 韬,杨柳晓. 考虑兼职的客服排班实时调整研究
Study on Real-Time Adjustment of Customer Service Scheduling Considering Part-Time Staff[J]. 服务科学和管理, 2020, 09(01): 26-34. https://doi.org/10.12677/SSEM.2020.91003
参考文献
- 1. 孙伟, 苏浩. 浅谈客户服务在企业发展中的作用[J]. 财经界(学术版), 2011(18): 109-109.
- 2. 沈颂东, 丛丽. 呼叫中心服务质量测评模型的构建与分析[J]. 经济管理, 2011, 33(11): 54-60.
- 3. Mehrotra, V., Wright, C. and Patel, S. (2009) An Investigation into the Business Processes, Job Descriptions, and Human Resource Factors Associated with Successful Workforce Management Practice. Working Paper, San Francisco State University, San Francisco, CA.
- 4. 阚泽正, 金兆正, 杨紫淇, 赵礼强. 零工经济背景下大学生兼职市场调研分析[J]. 现代商业, 2018(23): 164-165.
- 5. Warburg, V., Hansen, T.G., Larsen, A., Norman, H. and Andersson, E. (2008) Dynamic Airline Sche-duling: An Analysis of the Potentials of Refleeting and Retiming. Journal of Air Transport Management, 14, 163-167.
https://doi.org/10.1016/j.jairtraman.2008.03.004 - 6. Easton, F.F. and Goodale, J.C. (2005) Schedule Recovery: Unplanned Absences in Service Operations. Decision Sciences, 36, 459-488.
https://doi.org/10.1111/j.1540-5414.2005.00080.x - 7. Gans, N., Shen, H. and Zhou, Y.P. (2015) Parametric Stochastic Programming Models for Call Center Workforce Scheduling. Manufacturing & Service Operations Man-agement, 17, 1-33.
https://doi.org/10.1287/msom.2015.0546 - 8. Liao, S.Q. (2011) Staffing and Shift-Scheduling of Call Centers under Call Arrival Rate Uncertainty. Ecole Centrale Paris, Châtenay-Malabry.
- 9. Mehrotra, V., Ozluk, O. and Saltzman, R. (2010) Intelligent Procedures for Intra-Day Updating of Call Center Agent Schedules. Production and Operations Management, 19, 353-367.
https://doi.org/10.1111/j.1937-5956.2009.01097.x
