Dynamical Systems and Control
Vol.05 No.01(2016), Article ID:16766,13
pages
10.12677/DSC.2016.51003
The Lie-Symmetry Analysis of (1 + 2)-Coupled Nonlinear Schrodinger Equations
Dongdong Xu1, Chaolu Temuer2*
1Inner Mongolia University, Hohhot Inner Mongolia
2Colledge of Arts and Sciences, Shanghai Maritime University, Shanghai

Received: Dec. 20th, 2015; accepted: Jan. 10th, 2016; published: Jan. 14th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
For a class of (1 + 2)-dimensional nonlinear Schrödinger equations, 8-dimensional subalgebra of the infinite Lie algebra is found and its one optimal system is constructed. By further reduction with its symmetry we obtain the corresponding ordinary differential equations. Solving the ordinary differential equations, one finds some exact invariant solutions of the Schrödinger equations.
Keywords:Nonlinear Schrodinger Equation, Lie Algebra, Optimal System, Invariant Solutions

一类(1 + 2)-维非线性薛定谔方程的Lie-对称分析
徐冬冬1,朝鲁2*
1内蒙古大学,内蒙古 呼和浩特
2上海海事大学文理学院,上海

收稿日期:2015年12月20日;录用日期:2016年1月10日;发布日期:2016年1月14日

摘 要
本文中,作者用对称方法研究了一类(1 + 2)-维非线性薛定谔方程组。首先,给出了它的无穷维Lie代数及其8-维有限子代数,并计算确定了该有限维8-维子代数的1-维子代数优化系统;其次,用获得的优化系统对原(1 + 2)方程进行了对称约化,化其为一系列低维方程;第三,对已经约化的低维方程再次用对称方法进行约化获得一系列常微分方程;解该常微分方程得到了原(1 + 2)-维薛定谔方程组的精确解。
关键词 :非线性薛定谔方程,Lie对称,优化系统,不变解

1. 引言
本文用Lie对称方法研究了求解如下(1 + 2)-维非线性立方薛定谔方程(2D-CNLS)
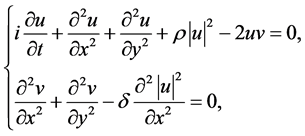 (1)
(1)
的精确解的问题,其中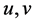 是自变量
是自变量 的复函数,
的复函数,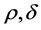 是常数。该方程组在诸多科学领域有重要的应用,包括非线性光学、超导电性、量子力学和等离子物理等,它也可以作为研究Bose-Einstein的简化模型 [1] - [4] 。方程(1)也描述地球引力下2-维水波的传播 [1] [2] 。对方程(1)的精确求解已经有了一些研究 [1] - [4] 。在文 [3] 中作者用双线性方法给出了快速下降解,在 [4] 中给出了相似约化结果 [4] 。据作者所知该方程的对称优化系统下的分析和求解还没有讨论。本文中,我们利用Lie-对称方法对该2D-CNLS方程的求解问题进行了研究。确定其拥有Lie代数及其优化系统,将方程约化为常微分方程组,进而精确求解。
是常数。该方程组在诸多科学领域有重要的应用,包括非线性光学、超导电性、量子力学和等离子物理等,它也可以作为研究Bose-Einstein的简化模型 [1] - [4] 。方程(1)也描述地球引力下2-维水波的传播 [1] [2] 。对方程(1)的精确求解已经有了一些研究 [1] - [4] 。在文 [3] 中作者用双线性方法给出了快速下降解,在 [4] 中给出了相似约化结果 [4] 。据作者所知该方程的对称优化系统下的分析和求解还没有讨论。本文中,我们利用Lie-对称方法对该2D-CNLS方程的求解问题进行了研究。确定其拥有Lie代数及其优化系统,将方程约化为常微分方程组,进而精确求解。
本文框架如下:在第二节给出了方程(1)的Lie对称的无穷维Lie代数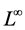 。为了应用方便我们确定了其一个8-维子代数
。为了应用方便我们确定了其一个8-维子代数 ;在第三节计算确定了该8-维子代数
;在第三节计算确定了该8-维子代数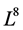 的一维优化系统;在第四节,用得到得优化系统对方程组(1)给出了第一次约化。把(1)化为一系列低维方程组;在第五节,对第四节获得的低维方程继续用其对称进一步约化获得一系列常微分方程组。至此把原(1 + 2)维2D-CNLS方程(1)约化为一系列常微分方程;在第六节,我们通过约化的常微分方程的求解获得原2D-CNLS方程(1)的精确。
的一维优化系统;在第四节,用得到得优化系统对方程组(1)给出了第一次约化。把(1)化为一系列低维方程组;在第五节,对第四节获得的低维方程继续用其对称进一步约化获得一系列常微分方程组。至此把原(1 + 2)维2D-CNLS方程(1)约化为一系列常微分方程;在第六节,我们通过约化的常微分方程的求解获得原2D-CNLS方程(1)的精确。
2. 方程组(1)的LIE代数
在本节我们将确定2D-CNLS方程组(1)的Lie代数(对称)。为了得到Lie代数,考虑单参数Lie对称群的无穷小变换 [5]
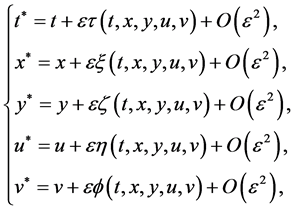 (2)
(2)
其中 是群参数,则其对应的Lie代数的生成元是
是群参数,则其对应的Lie代数的生成元是
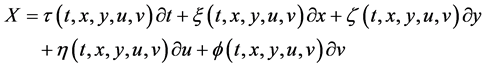
用文献 [6] [8] [9] 中给出的方法,我们求解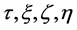 和
和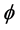 满足的确定方程组,得到
满足的确定方程组,得到
 (3)
(3)
其中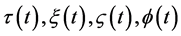 是任意函数。由此可知2D-CNLS方程组拥有Lie代数是无穷维的,其可应用于约化(1)的子代数很多。本文中选择任意函数
是任意函数。由此可知2D-CNLS方程组拥有Lie代数是无穷维的,其可应用于约化(1)的子代数很多。本文中选择任意函数 为如下形式
为如下形式
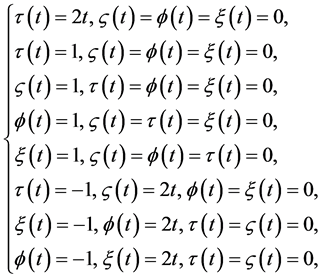
从而获得一个8-维Lie子代数,其无穷小变换生成元为:
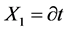 ,
,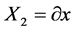 ,
,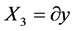 ,
,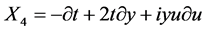 ,
,
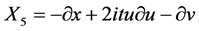 ,
,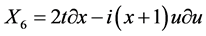 ,
,
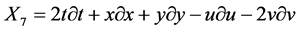 ,
,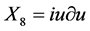 。
。
对以上生成元通过等价转换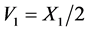 ,
,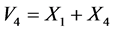 ,
, ,
,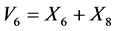 和
和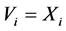 ,
,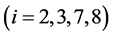 获得等价生成元
获得等价生成元
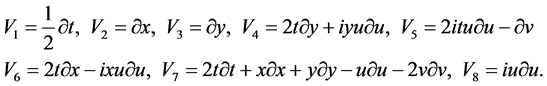 (4)
(4)
下面我们基于(4)研究(1)的约化和精确求解问题。
表1中给出了生成元(4)的交换关系。这种交换关系是计算由(4)生成Lie代数 优化系统的基础。
优化系统的基础。
3. Lie代数L8的1-维优化系统
在这部分,我们将给出由(4)生成的Lie代数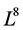 的1-维优化系统。构造Lie代数1-维优化系统等价于在该Lie代数伴随群变换下的子代数分类问题。
的1-维优化系统。构造Lie代数1-维优化系统等价于在该Lie代数伴随群变换下的子代数分类问题。
伴随群变换由以下Lie级数给出:
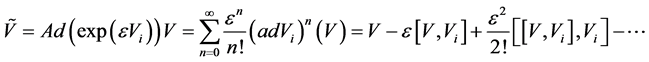 , (5)
, (5)
Table 1. Commutation of the Lie algebra [7]
表1. Lie代数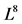 的交换表 [7]
的交换表 [7]
则称 与
与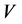 在伴随群下等价,记为
在伴随群下等价,记为 。
。
因此,在表2中给出了伴随变换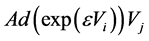 ,其中元
,其中元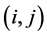 表示
表示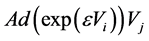 。
。
我们利用文献 [4] 中给出的方法,计算生成元(4)的1-维优化系统。过程如下:对于Lie代数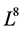 的任何非零元素
的任何非零元素
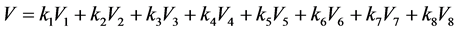 ,
,
作用伴随群尽可能的简化系数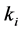 。易发现函数
。易发现函数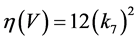 在伴随群作用下似不变的,即
在伴随群作用下似不变的,即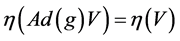 ,
,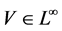 ,
, ,从而我们从该不变量入手讨论各类情况。
,从而我们从该不变量入手讨论各类情况。
情形1:若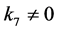 ,不妨设
,不妨设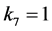 ,进而用
,进而用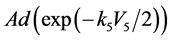 作用在
作用在 上,用(5)使得
上,用(5)使得 前的系数为零,即:
前的系数为零,即:
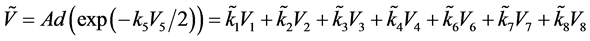 。
。
同样,依次地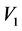 ,
,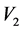 ,
,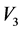 ,
,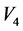 和
和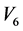 生成的伴随群(以下简称
生成的伴随群(以下简称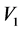 ,
,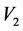 ,
,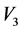 ,
,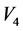 和
和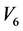 的作用),我们可以消除
的作用),我们可以消除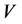 中
中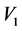 ,
,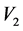 ,
,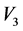 ,
, 和
和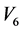 前的系数。因此,算子
前的系数。因此,算子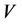 等价于
等价于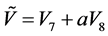 ,其中
,其中 。
。
情形2:若 ,假设
,假设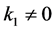 ,不妨设
,不妨设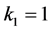 。依次通过
。依次通过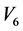 ,
,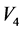 和
和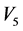 的作用,可以使得
的作用,可以使得 ,
,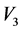 和
和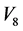 前的系数为零,因此
前的系数为零,因此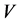 等价于
等价于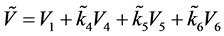 。由
。由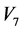 作用于
作用于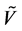 可得
可得
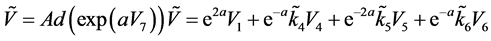 ,
,
即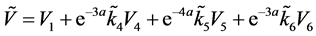 ,进一步可使
,进一步可使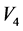 前的系数为
前的系数为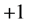 ,
,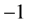 或0。这样我们得到
或0。这样我们得到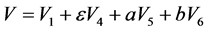 ,其中
,其中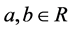 ,
,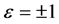 或0。
或0。
情形3:若 ,假设
,假设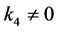 ,不妨设
,不妨设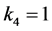 。依次由
。依次由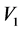 ,
,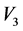 ,
,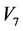 简化
简化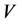 可得
可得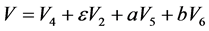 ,其中
,其中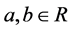 ,
,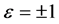 或0。
或0。
情形4:若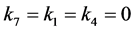 ,
,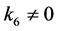 ,不妨设
,不妨设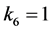 。依次由
。依次由 ,
,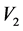 ,
,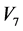 作用于
作用于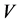 可得
可得 ,其中
,其中 ,
, 或0。
或0。
情形5:若 ,
,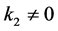 ,不妨设
,不妨设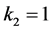 。依次由
。依次由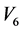 ,
,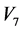 作用于
作用于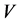 可得
可得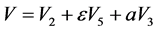 ,其中
,其中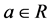 ,
, 或0。
或0。
情形6:若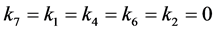 ,
,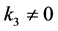 ,不妨设
,不妨设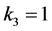 。依次由
。依次由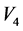 ,
,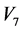 作用于
作用于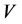 可得
可得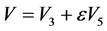 ,其中
,其中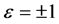 或0。
或0。
Table 2. Adjoint representation of basis element of Lie algebra
表2. Lie代数的基元素的伴随关系
情形7:若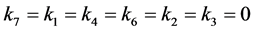 ,
, ,不妨设
,不妨设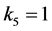 。由
。由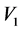 作用于
作用于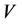 可得
可得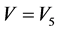 。
。
最后一种情形,当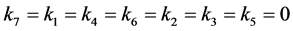 时,
时,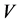 和
和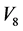 是等价的。
是等价的。
因此,我们得到无穷维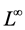 的子代数
的子代数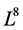 的一维优化系统生成元为
的一维优化系统生成元为
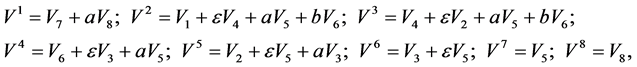 (6)
(6)
其中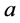 ,
,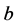 是任意常数,
是任意常数, 或0。
或0。
4. 方程组(1)的关于优化系统(6)的第一次约化
本节将应用优化系统(6),计算出2D-CNLS方程组(1)的对称约化分类。由于过程的类似性,我们只以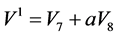 为例给出计算过程,其余的直接给出结果。
为例给出计算过程,其余的直接给出结果。
为了用对称约化方程组,我们必须解出对称的不变量,为此求解特征方程。如,生成元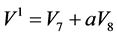 对应的特征系统为
对应的特征系统为
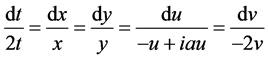 , (7)
, (7)
求解该方程组得到 的不变量如下
的不变量如下
 ,
, 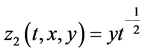 ,
, 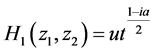 ,
,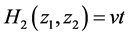 .
.
令
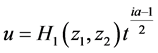 ,
, (8)
(8)
将(8)带入(1)得到(1)的约化方程为
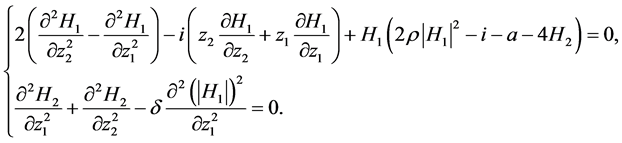 (9)
(9)
这个方程相比(1)少了一个自变量。
使用(6)中的其它生成元同样得到(1)的其他约化方程,结果列在表3中。
Table 3. The first reductions of (1) by optimal system (6)
表3. 方程组(1)关于优化系统(6)的第一次约化
其中:A: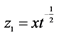 ,
,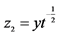 ,
,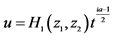 ,
, ;B:
;B: ,
, ,
,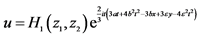 ,
,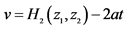 ;C:
;C: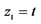 ,
,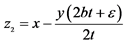 ,
,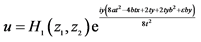 ,
, ;D:
;D: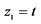 ,
,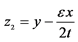 ,
, ,
,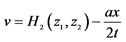 ;E:
;E: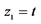 ,
,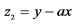 ,
,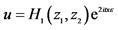 ,
,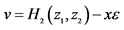 ;F:
;F: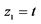 ,
,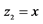 ,
,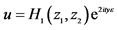 ,
,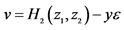 。
。
5. 通过表3中约化方程第二次约化2D-CNLS方程组(1)
对表3中A到F的每一个方程再运用与第四节采用的相同的对称约化过程,就得到表3中方程的进一步降维。从而得到原方程(1)的进一步约化,即相应的常微分方程。
我们以表3中的F对应的方程为例,给出方程组(1)的第二次约化过程。取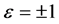 ,我们得到如下方程组
,我们得到如下方程组
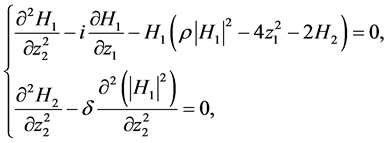
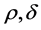 为常数 (10)
为常数 (10)
方程组(10)的Lie代数对称群为
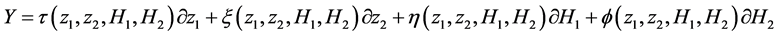 。
。
用文献 [8] [9] 中的方法解 和
和 的决定方程组,即
的决定方程组,即
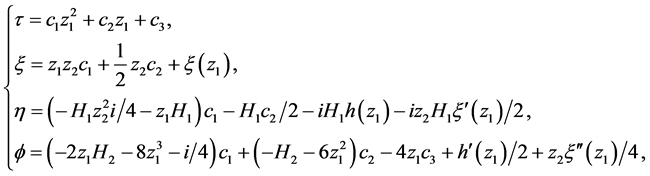 (11)
(11)
其中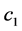 ,
,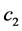 ,
,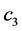 是任意的常数,
是任意的常数,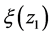 ,
, 是任意的函数。
是任意的函数。
方程组(10)拥有的Lie代数也是无穷维的,且有结构: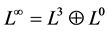 。
。
其中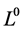 是以下在(11)中含有任意函数的生成元
是以下在(11)中含有任意函数的生成元
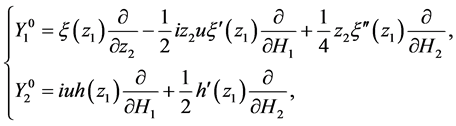 (12)
(12)
确定的无穷维子代数,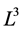 是(11)中任意常数对应的有限维部分。
是(11)中任意常数对应的有限维部分。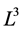 的一组基为
的一组基为
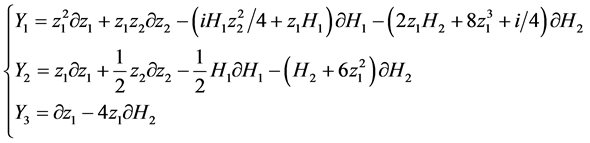 (13)
(13)
令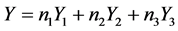 为3-维空间
为3-维空间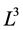 的任意元素。容易发现
的任意元素。容易发现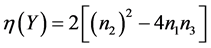 使伴随群的不变量。依次由
使伴随群的不变量。依次由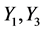 作用于
作用于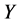 ,可得:
,可得:

其中
Table 4. Commutators of (13)
表4. (13)的交换表
Table 5. Commutators of (13)
表5. (13)的交换表

依赖于不变量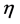 的3种情形如下:
的3种情形如下:
情形1:如果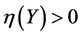 ,存在实数
,存在实数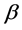 使得二次方程
使得二次方程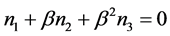 ,并且取
,并且取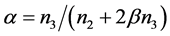 ,则
,则 ,此时,
,此时,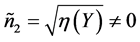 。因此
。因此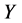 等价于
等价于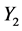 。
。
情形2:如果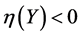 ,令
,令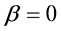 ,
, ,使得
,使得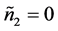 。由
。由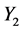 作用于
作用于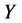 ,使得
,使得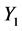 和
和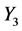 前的系数相等。因此
前的系数相等。因此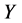 等价于
等价于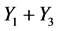 。
。
情形3:如果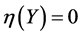 ,则有两种情况。若
,则有两种情况。若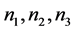 不全为零,我们可以选择
不全为零,我们可以选择 和
和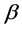 使得
使得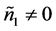 ,
,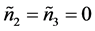 ,这时
,这时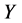 等价于
等价于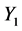 。
。
总之,3-维子代数的一维优化系统为:
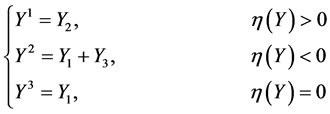 (14)
(14)
因此,我对(10)可用(14)进行约化,约化结果见表6。
同样的过程对表3种的其他情况可给出约化结果。由于篇幅有限,这里省略。
6. 方程组(1)的部分精确不变解
本节通过求解表6中的常微分方程,将给出(1)的精确解。
我们举两个例子说明,其余情形同样处理。
例1:对表6中的方程
 (15)
(15)
Table 6. The second reductions of (1) with
表6. 方程(10)关于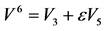 的简化
的简化
其中:A: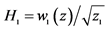 ,
,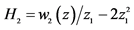 ,
, ;B:
;B: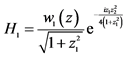 ,
, ,
,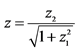 ;C:
;C: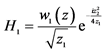 ,
,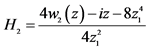 ,
, 。
。
令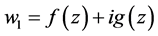 ,其中
,其中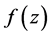 和
和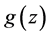 是实函数,带入(15)中可得
是实函数,带入(15)中可得
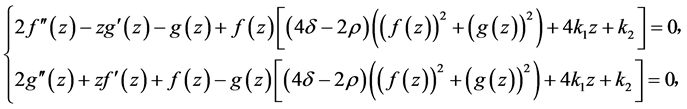 (16)
(16)
其中 是任意常数。很难求得方程(16)的通解。因此,取
是任意常数。很难求得方程(16)的通解。因此,取 ,
,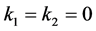 ,即把(16)变为
,即把(16)变为 ,解出其解
,解出其解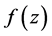 与
与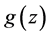 如下
如下
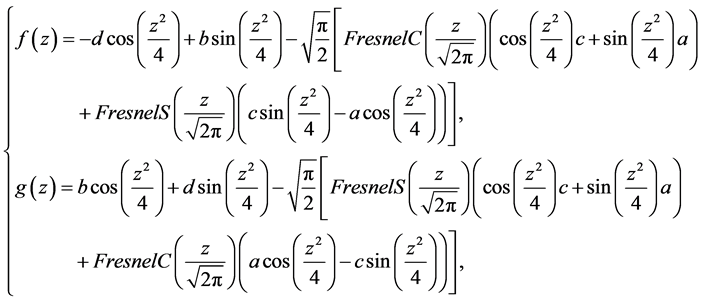
其中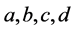 是任意常数,
是任意常数,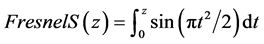 ,
,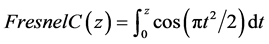 。考虑一个特殊的情形:
。考虑一个特殊的情形: ,这时有
,这时有
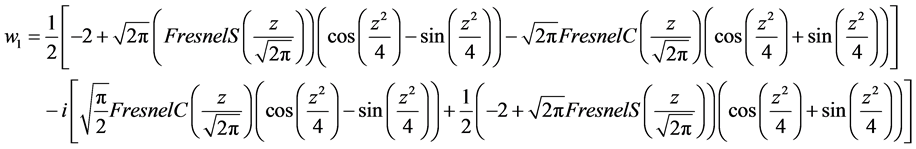
图1~3给出 与
与 的图像。
的图像。
方程(1)对应的精确解为:
 (17)
(17)
其中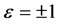 ,
,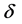 为常数。
为常数。
例2:考虑表6中的方程
用相同的方法,方程简化为
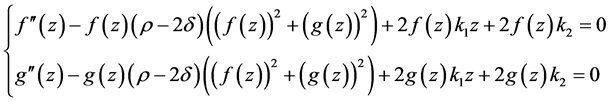
令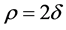 ,
,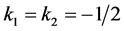 ,上式化简为:
,上式化简为:
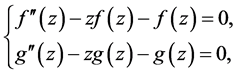
解方程组得:
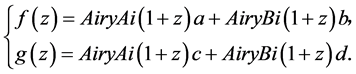
选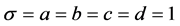 ,得到
,得到
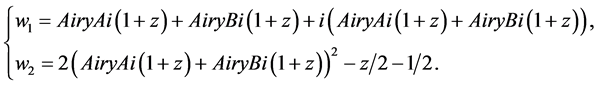
方程组(1)对应的精确解为
 (18)
(18)
其中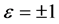 。
。
从图1到图5,可以发现方程组(1)的解(17)和(18)有明显不同的特点。也就是说,在优化系统中不同的对称群生成方程(1)的不同性质的精确解。

Figure 1. Graph of 
图1. 的图像
的图像
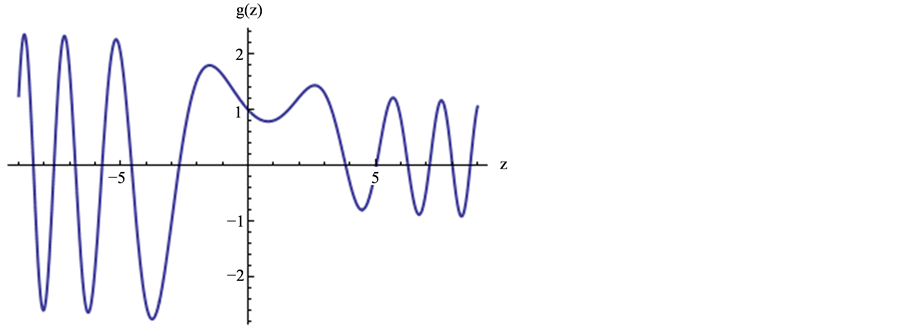
Figure 2. Graph of 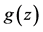
图2.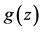 的图像
的图像
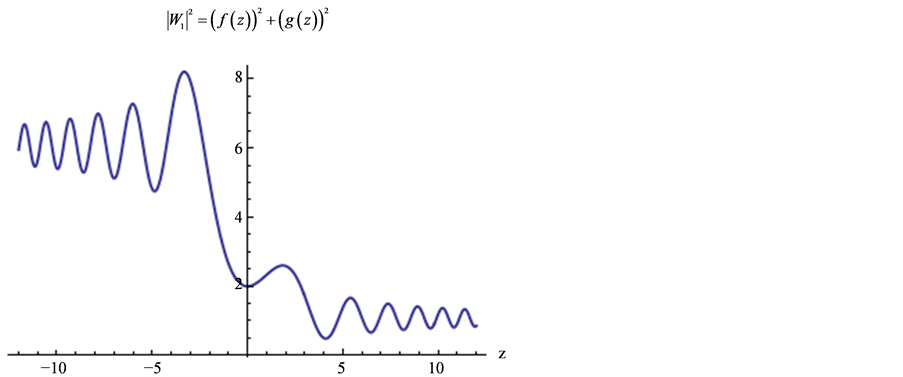
Figure 3. Graph of 
图3. 的图像
的图像
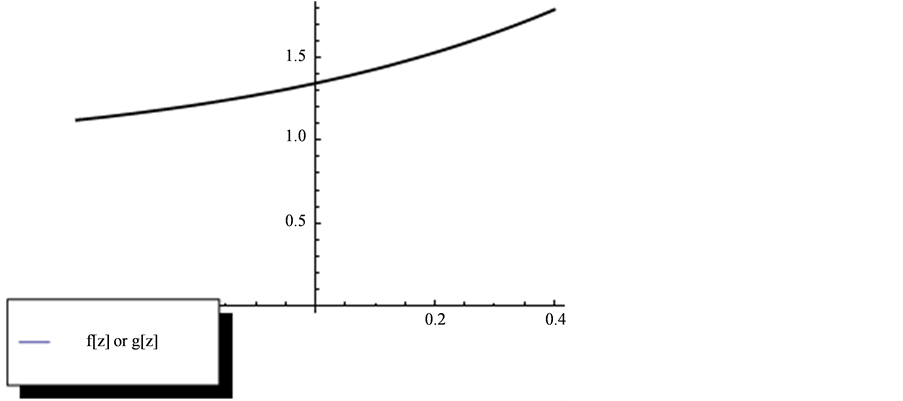
Figure 4. Graph of  or
or 
图4. 或
或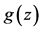 的图像
的图像
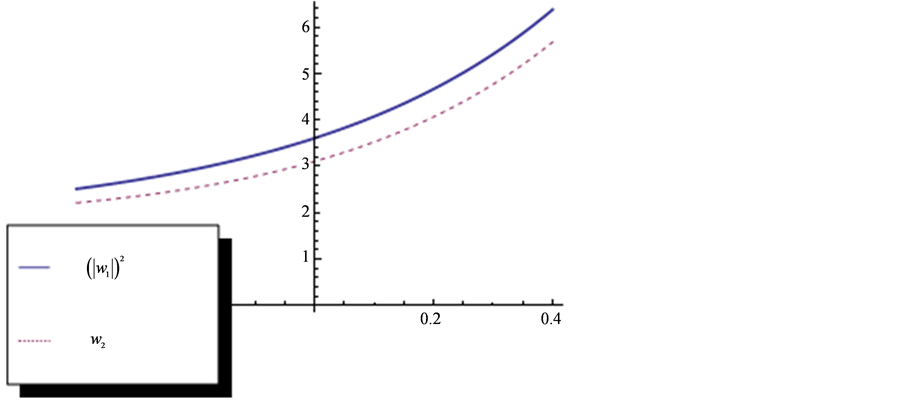
Figure 5. Graph of 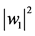 and
and 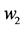
图5.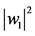 和
和 图像
图像
7. 结束语
本文应用对称方法约化和求解方程组(1)。文中没有直接的使用整体对称,而是使用了方程组(1)拥有对称的优化系统。这样做一方面简化计算过程,另一方面获得不同性质(非等甲类)的精确解。因为应用一次对称约化,方程中就减少一个自变量,因此,对方程组(1)连续的应用了两次对称约化把方程转化为一类常微分方程。求解该常微分方程得到方程组(1)的一些精确解。本文完整地呈现了对称方法的应用,并说明对称方法在求解偏微分方程的有效性,从具有工程应用的前景和价值。
致谢
感谢国家自然科学基金(No. 11571008)项目的支持。
文章引用
徐冬冬,朝 鲁. 一类(1 + 2)-维非线性薛定谔方程的Lie-对称分析
The Lie-Symmetry Analysis of (1 + 2)-Coupled Nonlinear Schrodinger Equations[J]. 动力系统与控制, 2016, 05(01): 18-30. http://dx.doi.org/10.12677/DSC.2016.51003
参考文献 (References)
- 1. Benney, D.J. and Roskes, G.J. (1969) Wave Instabilities. Studies in Applied Mathematics, 48, 377-385. http://dx.doi.org/10.1002/sapm1969484377
- 2. Davey, A. and Stewartson, K. (1974) On Three-Dimensional Packets of Surface Waves. Proceedings of the Royal Society of London. Series A, 388, 101-110. http://dx.doi.org/10.1098/rspa.1974.0076
- 3. Nakamura, A. (1982) Simple Multiple Explode-Decay Mode Solu-tions of a Two-Dimensional Nonlinear Schrödinger Equation. Journal of Mathematical Physics, 23, 417. http://dx.doi.org/10.1063/1.525361
- 4. Nakamura, A. (1982) Explode-Decay Mode Lump Solitons of a Two-Dimensional Nonlinear Schrödinger Equation. Physics Letters A, 88, 55-56. http://dx.doi.org/10.1016/0375-9601(82)90587-4
- 5. Kanth, A.S.V. and Aruna, K. (2009) Two-Dimensional Differential Transform Method for Solving Linear and Non-Linear Schrödinger Equations. Chaos, Solitons & Fractals, 41, 2277-1833. http://dx.doi.org/10.1016/j.chaos.2008.08.037
- 6. Chaolu, T. and Li, A. (2014) Lie Symmetries, One-Dimensional Optimal System and Optimal Reductions of (2+1)- Coupled Nonlinear Schrödinger Equations. Journal of Applied Mathematics and Physics, 2, 667-690.
- 7. Ovsyannikov, L.V. (1982) Lectures on the Theory of Group Properties of Differential Equations. Higher Education Press, Beijing.
- 8. Olver, P.J. (1998) Applications of Lie Groups to Differential Equations. 2nd Edition, Spronger-Verlag New York Berlin Heidelberg, New York.
- 9. Chaolu, T. and Jing, P. (2010) An Algorithm for the Completes Symmetry Classification of Differential Equations Based on Wu’s Method. Journal of Engineering Mathematics, 66, 181-199. http://dx.doi.org/10.1007/s10665-009-9344-5
*通讯作者。

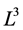 我们可以得到
我们可以得到