Dynamical Systems and Control
Vol.06 No.03(2017), Article ID:21300,10
pages
10.12677/DSC.2017.63014
Different Structure Synchronization of Fractional-Order Hyperchaotic Systems Based on Matrix Sliding Mode Structure
Shuang Liu, Lu Chen, Tao Wang, Lijuan Yue*
College of Physics, Northeast Normal University, Changchun Jilin

Received: Jun. 15th, 2017; accepted: Jul. 7th, 2017; published: Jul. 10th, 2017

ABSTRACT
A sliding mode control method is proposed for different structure synchronization of fractional- order hyperchaos system. Under the action of the new matrix sliding mode controller, different structure synchronization of fractional-order hyperchaotic systems has been realized. Experimental results show that the method has stronger robustness, and furthermore, circuit simulations show the effectiveness of the proposed method.
Keywords:Fractional-Order Hyperchaos System, Matrix Theory, Sliding Mode Variable Structure Control, Hyper-Chaotic Synchronization
矩阵滑模控制法实现异结构分数阶超混沌 系统同步
刘爽,陈璐,王涛,岳立娟*
东北师范大学 物理学院,长春

收稿日期:2017年6月15日;录用日期:2017年7月7日;发布日期:2017年7月10日

摘 要
针对分数阶超混沌系统的异结构同步问题,提出了一种矩阵滑模控制方法,设计了一个新的滑模控制器。在该控制器的作用下实现了分数阶超混沌系统的异结构同步,实验结果表明该方法具有较强的鲁棒性,电路仿真证明了控制器的有效性。
关键词 :分数阶超混沌系统,矩阵理论,滑模变结构控制,超混沌同步

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近年来混沌被证实广泛存在于物理 [1] [2] 、生物 [3] 、通信保密 [4] [5] 等领域中。从1979年若斯勒发表第一个超混沌系统 [6] ,人们对超混沌系统研究逐渐深入,对整数阶超混沌系统的研究也取得了诸多成果。而由于分数阶混沌系统比整数阶混沌系统具有更复杂的动力学特性,因此分数阶混沌系统逐步成为了近代研究的热点之一,如分数阶Chen系统 [7] ,分数阶Lorenz系统 [8] ,分数阶Liu系统 [9] ,分数阶Rossler系统 [10] 及新的分数阶超混沌系统 [11] 等。二十世纪九十年代初,美国科学家L. M. Pecora和T. L. Carrol提出混沌自同步方法 [12] ,至今混沌同步控制方法已经发生了巨大的变化,形成了一系列的同步控制方法,如脉冲法 [13] 、自适应法 [14] 、状态观测器法 [15] 、神经网络法 [16] 、滑模变结构法 [17] 。滑模变结构法因其有较高的鲁棒性、控制器设计简单等特点被广泛地应用在混沌系统的控制中,用传统的混沌控制方法与滑模控制理论相结合更是成为近年研究的热点,Jui-sheng Lin [18] 等人应用自适应滑模控制方法实现了混沌系统的同步,同时Sara Dadras [19] 等人也提出了一种新的滑模控制方法,实现了对参数不确定了Liu混沌系统的控制。
本文基于分数阶稳定性定理和Lyapunov稳定性定理将矩阵理论和滑模变换结构控制相结合,设计一个新的滑模控制器,实现分数阶超混沌系统的异结构同步,利用Matlab数值模拟和Multisim电路仿真证明了矩阵滑模控制法的有效性,控制器简单易实现,鲁棒性更强。
2. 矩阵理论
微分和积分Caputo定义为:
一个 阶的Riemann-Liouville积分算子
阶的Riemann-Liouville积分算子
 (1)
(1)
其中 为Gamma函数,则
为Gamma函数,则 阶Caputo微分算子
阶Caputo微分算子 定义为:
定义为:
 (2)
(2)
 为第一个不小于
为第一个不小于 的正整数,
的正整数,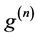 为
为 的
的 阶导数。
阶导数。
分数阶系统如下:
 (3)
(3)
 (4)
(4)
其中 ;
; 为非线性控制器。
为非线性控制器。

系统误差量定义为:
 (5)
(5)
则误差系统为:
 (6)
(6)
定理1. 若加入合适的非线性控制器 ,使误差系统变为:
,使误差系统变为:
 (7)
(7)
其中 ,且满足
,且满足
(1) 
(2)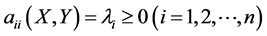 且
且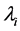 不全为0,
不全为0,
则分数阶误差系统(6)是渐近稳定,分数阶混沌系统(3)和(4)实现同步。
驱动系统 [20] 为:
 (8)
(8)
响应系统 [21] 为:
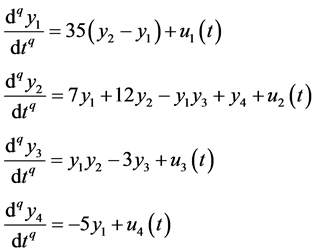 (9)
(9)
定义误差 ,则误差系统为:
,则误差系统为:
 (10)
(10)
设计控制器如下:
 (11)
(11)
可知系数矩阵为:

上式满足定理1,所以响应系统(9)与新分数阶超混沌系统(8)实现同步。
取驱动系统(8)和响应系统(9)的初值为 ,
, ,
, ,
,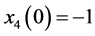 ,
, ,
, ,
, ,
, 。由图1矩阵理论法数值模拟的误差结果可以看出加入控制项后使系统稳定。
。由图1矩阵理论法数值模拟的误差结果可以看出加入控制项后使系统稳定。
混沌系统往往会受到外界的干扰而影响同步效果,基于矩阵理论控制器下数值模拟的结果如图2所示。在干扰较小时系统同步结果并未受到影响,如图2(a),而在干扰较大时,系统不能达到同步,如图2(b)所示。
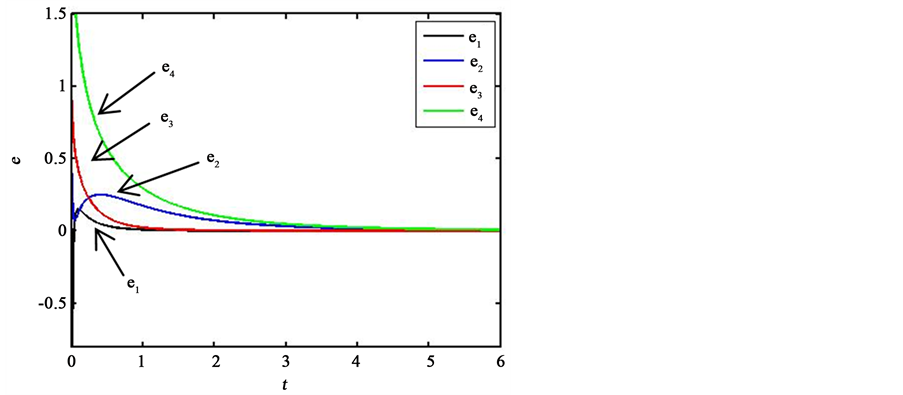
Figure 1. The state trajectory of the error system for Matrix theory
图1. 矩阵理论法的误差曲线

 (a) (b)
(a) (b)
Figure 2. The curve after disturbance of . (a) The error curve of the interference is
. (a) The error curve of the interference is ; (b) The error curve of the interference is
; (b) The error curve of the interference is 
图2. 受干扰后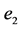 随时间变化曲线。(a)干扰为
随时间变化曲线。(a)干扰为 时
时 的曲线;(b)干扰为
的曲线;(b)干扰为 时
时 的曲线
的曲线
3. 矩阵滑模控制
矩阵理论与滑模控制相结合设计一个合适的滑模控制器,使误差系统(10)的轨迹到达滑模面并趋于稳定,根据滑模控制原理,首先设计滑模面:
 (12)
(12)
定义函 满足如下方程:
满足如下方程:
 (13)
(13)
由于当系统运动到滑模面时,需要满足:
 (14)
(14)
由此可得到:
 (15)
(15)
结合误差系统(10)得到等效控制器 为:
为:
 (16)
(16)
由于滑模变结构控制本身具有抖振现象,为了减小抖振的影响,提高趋近品质,应该选择合适的趋近律。由于指数趋近律的趋近速度快,同时可以通过调节系数 和
和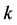 来改变达到滑模面的速度,并在一定程度上抑制了抖振现象,所以本文选取了指数趋近律,如下:
来改变达到滑模面的速度,并在一定程度上抑制了抖振现象,所以本文选取了指数趋近律,如下:
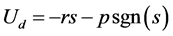 (17)
(17)
其中 ,
, 是符号函数,并满足如下条件:
是符号函数,并满足如下条件:
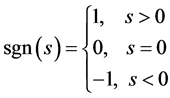
最终得到控制器如下:
 (18)
(18)
根据滑模控制原理,若使误差系统的运动轨迹能够到达滑模面上,必需满足条件:
 (19)
(19)
证明:构造如下Lyapunov函数

对其求导可得:

由于 ,则可得到
,则可得到 ,满足滑模到达条件,所以误差系统的运动轨迹可以运动到滑模面上。
,满足滑模到达条件,所以误差系统的运动轨迹可以运动到滑模面上。
选取步长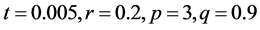 驱动系统和响应系统的初值分别为
驱动系统和响应系统的初值分别为 ,
, ,
, ,
, ,
, ,
,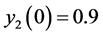 ,
,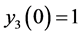 ,
,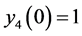 ,由图3的数值仿真结果可以看出,矩阵滑模法与矩阵理论方法相比之下能够更快地使驱动系统和响应系统达到同步,同步效果更明显。
,由图3的数值仿真结果可以看出,矩阵滑模法与矩阵理论方法相比之下能够更快地使驱动系统和响应系统达到同步,同步效果更明显。

Figure 3. The state trajectory of the error system for Matrix sliding mode
图3. 矩阵滑模控制法的误差曲线
在较大干扰 时,仿真结果如图4所示。与矩阵理论控制下的同步效果相比较,可以看出基于矩阵滑模控制器下,响应系统与驱动系统在较大干扰下仍然可以达到同步,说明此方法具有较强的鲁棒性。
时,仿真结果如图4所示。与矩阵理论控制下的同步效果相比较,可以看出基于矩阵滑模控制器下,响应系统与驱动系统在较大干扰下仍然可以达到同步,说明此方法具有较强的鲁棒性。
由于受输出幅度的限制,现将驱动系统的状态变量缩小2倍,则驱动系统变为:
 (20)
(20)
分数阶超混沌系统的积分算子等效电路如图5,其中 ,
, ,
, ,
, ,
, ,
, 。
。
本文采用Multisim12.0作为电路仿真平台,根据驱动系统(20)设计仿真电路如图6所示。其中电源电压为 ,运算放大器为LM741,乘法器为AD534。
,运算放大器为LM741,乘法器为AD534。
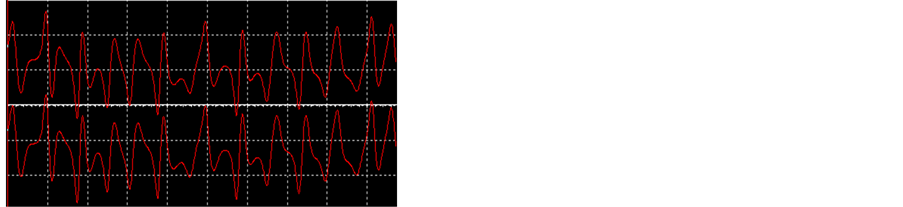
对矩阵滑模控制法进行电路仿真,仿真结果如图7所示。结果显示驱动系统的响应系统能够很快达到同步,这与数值模拟的结果相同,再次证明了矩阵滑模控制器的有效性。

Figure 4. The curve after disturbance of 
图4. 受干扰后 随时间变化曲线
随时间变化曲线

Figure 5. The equivalent circuit of fractional integral operator unit
图5. 分数阶积分算子单元电路的等效电路

Figure 6. Driving system circuit
图6. 驱动系统(20)电路
 (a) (b)
(a) (b)
 (c) (d)
(c) (d)
Figure 7. The synchronous circuit simulation results of Matrix sliding mode. (a) The time domain of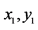 ; (b) The time domain of
; (b) The time domain of ; (c) The time domain of
; (c) The time domain of ; (d) The time domain of
; (d) The time domain of 
图7. 矩阵滑模控制法的电路仿真同步结果。(a) 的时域图;(b)
的时域图;(b) 的时域图;(c)
的时域图;(c) 的时域图;(d)
的时域图;(d) 的时域图
的时域图
4. 结论
本文基于Lyapunov稳定性理论,将滑模变结构方法与矩阵理论相结合,设计了一种新的控制器,实现了分数阶超混沌系统的异结构同步。数值仿真的结果表明矩阵理论结合滑模的方法较矩阵理论方法控制效果好,并具有控制时间短、鲁棒性强等优点。电路仿真的结果证明了该控制器的有效性,具有广阔的应用前景。
致谢
本文得到国家自然科学基(批准号:10847110)和吉林省自然科学基金(批准号:201115008)的资助,在此表示感谢。
基金项目
国家自然科学基金(批准号:10847110)和吉林省自然科学基金(批准号:201115008)。
文章引用
刘 爽,陈 璐,王 涛,岳立娟. 矩阵滑模控制法实现异结构分数阶超混沌系统同步
Different Structure Synchronization of Fractional-Order Hyperchaotic Systems Based on Matrix Sliding Mode Structure[J]. 动力系统与控制, 2017, 06(03): 109-118. http://dx.doi.org/10.12677/DSC.2017.63014
参考文献 (References)
- 1. 李佳. 物理中投影混沌同步在永磁同步电机中的应用[J]. 高师理科学刊, 2016, 36(1): 39-42.
- 2. 贾遂民, 魏萌, 胡明生. 混沌拟态物理优化的认知频谱差异分配[J]. 计算机应用, 2015, 35(4): 1067-1070.
- 3. 郑金存, 张慧, 覃斌毅. 变参数混沌信号应用于经皮神经电刺激的探索研究[J]. 生物医学工程学杂志, 2015, 32(5): 1031-1037.
- 4. 俞斌, 朱明, 贾雅琼. 统一混沌系统同步控制及在保密通信中的应用[J]. 计算机应用研究, 2013, 30(6): 1847- 1848.
- 5. Lai, H. and Huang, Y. (2015) Chaotic Secure Communication Based on Synchronization Control of Chaotic Pilot Signal. Computational Intelligence and Intelligent Systems, 2015, 640-647.
- 6. Rossler, O. (1979) An Equation for Hyperchaos. Physics Letters A, 71, 155-157. https://doi.org/10.1016/0375-9601(79)90150-6
- 7. Li, C. and Peng, G. (2004) Chaos in Chen’s System with a Fractional Order. Chaos, Solitons & Fractals, 22, 443-450. https://doi.org/10.1016/j.chaos.2004.02.013
- 8. Jia, H.Y., Tao, Q. and Chen, Z.Q. (2014) Analysis and Circuit Design of a Fractional-Order Lorenz System with Different Fractional Orders. Systems Science & Control Engineering, 2, 745-750. https://doi.org/10.1080/21642583.2014.886310
- 9. Hegazi, A.S., Ahmed, E. and Matouk, A.E. (2013) On Chaos Control and Synchronization of the Commensurate Fractional Order Liu System. Communications in Nonlinear Science & Numerical Simulation, 18, 1193-1202. https://doi.org/10.1016/j.cnsns.2012.09.026
- 10. Li, C.G. and Chen, G.R. (2004) Chaos and Hyperchaos in the Fractional Order Rössler Equations. Physica A: Statistical Mechanics and Its Applications, 341, 55-61. https://doi.org/10.1016/j.physa.2004.04.113
- 11. Razminia, A. and Baleanu, D. (2013) Complete Synchronization of Commensurate Fractional Order Chaotic Systems Using Sliding Mode Control. Mechatronics, 23, 873-879. https://doi.org/10.1016/j.mechatronics.2013.02.004
- 12. Carroll, T.L. and Pecora, L. (1992) A Circuit for Studying the Synchronization of Chaotic Systems. International Jour- nal of Bifurcation and Chaos, 2, 659-667. https://doi.org/10.1142/S021812749200077X
- 13. Itoh, M., Yang, T. and Chua, L.O. (2011) Conditions for Im-pulsive Synchronization of Chaotic and Hyperchaotic Systems. International Journal of Bifurcation and Chaos, 11, 551-560. https://doi.org/10.1142/S0218127401002262
- 14. Sinha, S., Henrichs, J. and Ravindra, B. (2000) A General Approach in the Design of Active Controllers for Nonlinear Systems Exhibiting Chaos. International Journal of Bifurcation and Chaos, 10, 165-178. https://doi.org/10.1142/S0218127400000104
- 15. 刘福才, 王娟, 彭海朋, 等. Hénon混沌系统的预测控制与同步[J]. 物理学报, 2002, 51(9): 1954-1959.
- 16. 谭文, 王耀南, 刘祖润. 非线性系统混沌运动的神经网络控制[J]. 物理学报, 2005, 51(11): 2463-2466.
- 17. Ma, J., Wu, X.Y. and Chu, R.T. (2014) Selection of Multi-Scroll Attractors in Jerk Circuits and Their Verification Using Pepice. Nonlinear Dynamics, 76, 1951-1962. https://doi.org/10.1007/s11071-014-1260-1
- 18. Lin, J.S., Yan, J.J. and Liao, T.L. (2005) Chaotic Synchronization via Adaptive Sliding Mode Observers Subject to Input Nonlinearity. Chaos, Solitons & Fractals, 24, 371-381. https://doi.org/10.1016/S0960-0779(04)00616-2
- 19. Dadras, S., Momeni, H.R. and Majd, V.J. (2009) Sliding Mode Control for Uncertain New Chaotic Dynamical System. Chaos, Solitons & Fractals, 41, 1857-1862. https://doi.org/10.1016/j.chaos.2008.07.054
- 20. 董俊, 张广军, 姚宏. 异结构的分数阶超混沌系统函数投影同步及参数辨识[J]. 电子与信息学, 2013, 35(6): 1371-1375.
- 21. 周平, 程雪峰, 张年英. 一个新分数阶超混沌系统及其混沌同步[J]. 物理学报, 2008, 57(9): 5407-5412.
NOTES
*通讯作者。