Dynamical Systems and Control
Vol.
08
No.
01 (2019
), Article ID:
28070
,
8
pages
10.12677/DSC.2019.81003
Research on the Mode Calculation and Characteristic Modularization of the Gas Turbine in the Power System
Guang Xu1, Baihui Xu1, Qianchao Liang2, Hen Qin2
1Naval Equipment Section of the East China Sea Fleet, Ningbo Zhejiang
2College of Naval Architecture and Power, Naval University of Engineering, Wuhan Hubei
Received: Nov. 26th, 2018; accepted: Dec. 11th, 2018; published: Dec. 18th, 2018

ABSTRACT
In this paper, a joint power system control is taken as the research object, which solves the complicated logical relationship of the remote control system, the logical reasoning structure, and the control of the Ethernet system. The control system simulation is based on the system dynamics, nonlinear causes and calculation methods. It uses a quasi-steady state method, a volumetric method, and a wave action method to calculate a nonlinear system. It is pointed out that the dynamic characteristics of the power system will ultimately affect the design performance of the whole power plant.
Keywords:Power System Plant (CODOG), Modularization, Simulation
动力系统中燃气轮机特性仿真与计算方法研究
许光1,徐百汇1,梁前超2,秦珩2
1海军92910部队,浙江 宁波
2海军工程大学,湖北 武汉
收稿日期:2018年11月26日;录用日期:2018年12月11日;发布日期:2018年12月18日

摘 要
以某联合动力系统控制为研究对象,解决了遥控系统错综复杂的逻辑关系、逻辑推理结构、以太网络系统控制等问题。整个控制系统仿真从系统动力组成、非线性成因和计算方法的处理等方面,采用准稳态法、容积法和波动作用法计算等手段计算非线性系统,指出了动力系统的动态特性最终会影响整个动力装置的设计性能和输出结果。
关键词 :动力系统装置(CODOG),模块化,仿真

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 前言
动力系统建模方法多种多样并且非线性特征非常突出。动力系统的遥控系统逻辑关系非常错综复杂,逻辑推理必须要求设计和管理人员非常熟悉设备和管制系统,具备较丰富的系统控制知识和采取必要的科学手段。本文从系统动力组成、非线性成因和计算方法处理等方面,采用对实际系统进行抽象处理并将其特性用数学表达式进行描述,构成数学模型后再对数学模型进行仿真验证,最后得到计算结果。由于动力系统的遥控系统逻辑关系非常错综复杂、各种系统机构的质量惯性成为二阶系统模型及多阶的非线性系统,决定了动力系统的动态特性误差会影响整个动力装置的设计性能。
2. 系统建模方法介绍
根据仿真系统的结构和实现手段可以分为以下几类,即物理仿真、数学仿真、物理数学仿真 [1] [2] (也称半物理仿真或半实物仿真)。物理仿真是按照真实系统的物理性质构造系统的物理模型,并在物理模型上进行试验的过程。物理仿真的优点是直观、形象。数学仿真是对实际系统进行抽象,并将其特性用数学表达式描述系统而得到数学模型,再对数学模型进行试验的过程。数学仿真的缺点是受限于系统建模技术。物理数学仿真又称半实物仿真或半物理仿真,准确称谓为硬件在回路(Hardware in the loop)中的仿真。这种方法是将数学模型、物理模型和实物组合起来进行实验,对系统中比较简单的部分或规律比较清晰的部分建立数学模型,然后在计算机上加以实现;而对比较复杂的部分或规律尚不明确的系统,其数学模型建立比较困难,则采用物理模型或数学仿真。
涡轮机械中气体流动建模方法可以分为准稳态法、容积法和波动作用法。用于发动机动态过程控制的气体流动模型主要是准稳态模型和容积法模型,特征线法用于动态过程计算的情况很少见。准稳态方法是最简单的方法:它不涉及各部件内的详细工作过程,部件的特征由输入和输入出量间的关系表达,这些关系或通常由实验获得或者根据经验公式推测。容积法的基本特征是用有限容积来表示柴油机本体和增压器之间的管道以及气缸。系统的模型使用一组一阶微分方程组来描述管道、缸的状态以及在瞬态工况下发动机和增压器的转速。特征线法模型中用可压缩气体流动方程来表示在进排气管中存在的压力波动作用。这些特征线法的名称来源程序于求解偏微分方法通常采用的特征线方法。特征线法对于特定的发动机类型具有特别重要的意义。
文献 [3] [4] [5] 在MATLAB/Simulink平台基础上,利用容积惯性法,建立了某三轴燃气轮机的面对对象的非线性仿真模型,在此基础上分析了燃气轮机单机工作于全工况的负载特性,得到了为抛物线性关系燃气轮机全工况负荷效率特性。文献 [5] 建立了燃-燃联合动力装置的模型,仿真得到了船、机、桨等各种典型匹配情况下的推进特性,特别是单机单桨推进时整个动力装置的经济性最佳,舰艇的续航力达到最大值,对舰艇作战具有十分重要的军事意义。黄向华 [6] 等基于MATLAB/Simulink仿真平台,利用机理分析法(部件法)建立了燃气轮机的实时非线性数学模型,其中根据转速相似、流量相似和几何参数相似,把已知的部件参数按照比例关系转化到待建模的部件上,在一定程度上提高了燃气轮机建模的精度。文献 [4] [5] 建立了三轴模型,并且分别利用线性法和准线性法建立了三轴燃气轮机的数学模型,各自应用非稳态工况和稳态工作线为小偏差线性化起点,进行了某燃气轮机大扰动过程的计算,具有计算精度高、速度快的特点。结果表明模块化建模具有通用性,可以大大缩短建模的时间和重复劳动。
3. 系统数学模型仿真与推进系统的性能分析
系统仿真与推进系统性能分析必须进行建模,之后进行性能分析 [5] [7] 。黑箱模型的获得可以是先确定模型结构(图1),然后通过系统辩识方法获得模型参数。黑箱模型也可以完全不考虑系统结构,直接根据输入输出数据建立模型。
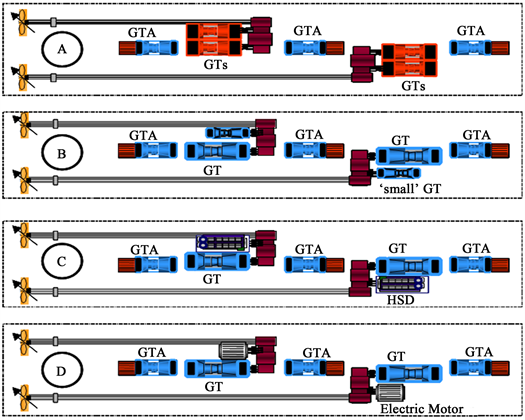
Figure 1. Power system model
图1. 动力系统模型
某三轴燃气轮机的数学模型。动力装置中的推进系统可能采用不同的推进方法和传动方式。虽然推进系统基本组成有很大的差别,但都可以概括为三大件:发动机、传动装置、推进器。对舰用燃气轮机装置,各部件热惯性影响不大,可以忽略。如不考虑热惯性,则主要有转动惯性和容积惯性。容积惯性相对于转动惯性要小的多,在以往的仿真计算中常忽略不计,即认为流量压力是瞬间平衡的。而在实际的动态过程中,流动的不平衡总是存在的,故本文中把容积惯性法引入到模块化建模中。由于对舰用燃气轮机的研究日益具体和深入,其数学模型比较成熟,可以直接根据物理模型建立某三轴燃气轮机转子和容积的运动方程为 [8] :
1) 惯性环节的微分方程式
(3.1.1)
(3.1.2)
(3.1.3)
(3.1.4)
(3.1.5)
 ( 3.1.6 )
( 3.1.6 )
(3.1.7)
式中:
、
、
分别为低、高压涡轮和动力涡轮的有效功率;
、
、
分别为低、高压压气机和负荷耗功率;
、
、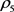 、
分别为容积
、
、
、
中的气体密度;
、
、
、
、
分别为低、高压压气机及高、低压动力涡轮中的进口流量;
、
、
、
分别为低、高压压气机和高、低压涡轮的出口流量;
、
、
分别为三只转子的角速度;
、
、
分别为三只转子的转动惯量;
、
分别为容积
、
、
、
中的气体密度;
、
、
、
、
分别为低、高压压气机及高、低压动力涡轮中的进口流量;
、
、
、
分别为低、高压压气机和高、低压涡轮的出口流量;
、
、
分别为三只转子的角速度;
、
、
分别为三只转子的转动惯量;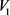 、
、
、
为容积。如果负荷是船舶的螺旋桨,由于螺旋桨特性和船体运动有关,还必须增加一个运动方程:
、
、
、
为容积。如果负荷是船舶的螺旋桨,由于螺旋桨特性和船体运动有关,还必须增加一个运动方程:
(3.1.8)
由于螺旋桨负荷的数学模型比较复杂,下面以该模型为主进行讨论,其它负荷以此类推。式中 为船体(包括粘附水)的质量, 为航速, 为螺旋桨推力,R为船体阻力。
2) 部件的特性方程组
(3.1.9)
(3.1.10)
 ( 3.1.11 )
( 3.1.11 )
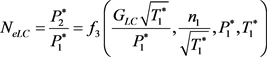 ( 3.1.12 )
( 3.1.12 )
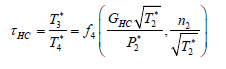 (3.1.13)
(3.1.13)
(3.1.14)
(3.1.15)
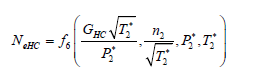 (3.1.16)
(3.1.16)
(3.1.17)
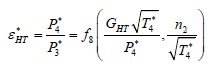 (3.1.18)
(3.1.18)
(3.1.19)
(3.1.20)
(3.1.21)
 (3.1.22)
(3.1.22)
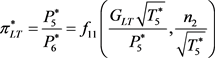 ( 3.1.23 )
( 3.1.23 )
(3.1.24)
(3.1.25)
(3.1.26)
(3.1.27)
(3.1.28)
(3.1.29)
负荷所消耗的有效功 取决于负荷特性,如负荷是螺旋桨,则增加三个方程:
(3.1.30)
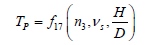 (3.1.31)
(3.1.31)
 (3.1.32)
(3.1.32)
以上诸式中H/D为螺旋桨的节径比,如果是定螺距的螺旋桨,此项就不做变量,可以从方程中去除。
3) 联系方程组
(3.1.33)
(3.1.34)
(3.1.35)
(3.1.36)
(3.1.37)
(3.1.38)
(3.1.39)
(3.1.40)
(3.1.41)
(3.1.42)
(3.1.43)
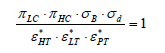 (3.1.44)
(3.1.44)
上述第一组方程惯性微分方程组是燃气轮机装置的稳态和动态计算的数学模型,而部件特性方程组和参数联系方程组是解此组方程所必备的辅助方程组。可见燃气轮机动态特性求解是归结为常微分方程组的求解问题。在动态计算中,常把上述微分方程成为状态方程,把方程左端的导数称为状态的导数,而状态则用向量X表示。如果把导数的系数移到等号右端,则动态系统的状态方程可以简单的用向量表示:
(3.1.46)
式中:
u为控制参数,包括油门杆角度、可调节距、可调喷嘴安装角等可调参数,X为n维向量, 为时间坐标。
第二组方程是部件特性,每个部件(压气机、涡轮)都整齐地用四个方程(温度比、压比、流量、功率)来表示。实际计算中,这些方程常常用曲线来描述,相应的算法用多元差值。值得主意的是上述部件如果是可调参数或控制参数(如压气机的可调进气口导叶、涡轮可调喷嘴等),则相应的特征方程中要增加可调参数作为自变量。至于负荷特性,则要说明是什么负荷,如果负荷是螺旋桨的话,需要增加三个方程,它们是螺旋桨的功率特性、推理特性和船体阻力特性。
第三组方程是用来联系特征截面上的参数,意义很明确,无需多加说明。
舰船联合动力装置性能分析。加速机和巡航机之间切换或并车时,要求拟投入运行的轴运速十分接近正在运行轴的转速时,才能将两根轴连接起来。自动同步离合器是达到这一要求的传动装置部件,目前应用较多的是带有棘齿同步机的自动同步离合器。在已进行的联欢合动力装置仿真中,通常是忽略自动同步离合器的动态啮合和税离过程,用逻辑表达式处理啮合前后轴转速的变化。对于柴燃关合动力装置控制系统的设计,大多数的工作集中在专业公司进行。从掌握的资料来看,只有英国YARD公司对柴燃交替动力装置进行了较多的工作。国内上海交通大学、海军论证中心等都对YARD公司提出CODOG舰船在各种工况下机动的要求。但正如YARD公司承认得那样,控制策略的设计主要是基于以前的相近系统的设计。这说明了舰船动力装置控制系统设计的复杂性和难度。COGAG动力装置正车推进可以分为单机两桨推进、两机两桨推进和四机两桨推进三种模式:
1) 单机两桨推进主要用于舰艇巡航及以下航速,此时燃气轮机的经济性相对较低,可以通过跨接齿轮箱实现任意一台燃气轮机带动两只螺旋桨工作,在一定程度上改善了燃机在低工况的经济性。
2) 两机两桨推进用于舰艇在巡航与全速之间的特定航速下航行,此工况下左右舷各一台燃机工作。
3) 四机两桨推进模式主要用于舰艇全速航行,长时间在此模式下工作会严重影响燃气轮机及动力装置的使用寿命。
4. 结论
动力系统中柴燃联合动力装置CODOG的系统结构非常复杂,建模方法也是多种多样,非线性特征非常突出。动力系统的遥控系统逻辑关系也非常错综复杂,逻辑推理必须要求设计和管理人员非常熟悉设备和管制系统,具备较丰富的系统控制知识和采取必要的科学手段。否则会发生误差大或不收敛的仿真计算后果。本文分析动力系统中的几个常见非线性仿真问题,从系统动力组成、非线性成因和计算方法等方面达到举一反三的目的,如果考虑变距机构的质量惯性,变距系统的模型成为二阶系统模型及多阶的非线性系统,决定了动力系统的动态特性会影响整个动力装置的设计性能。
文章引用
许 光,徐百汇,梁前超,秦 珩. 动力系统中燃气轮机特性仿真与计算方法研究
Research on the Mode Calculation and Characteristic Modularization of the Gas Turbine in the Power System[J]. 动力系统与控制, 2019, 08(01): 20-27. https://doi.org/10.12677/DSC.2019.81003
参考文献
- 1. Liu, B.J., Zhang, B. and Liu, Y.W. (2015) Investigation of Model Development for Deterministic Correlations Associated with Impeller Diffuser Interactions in Centrifugal Compressors. Science China (Technological Sciences), 58, 499-509.
https://doi.org/10.1007/s11431-015-5766-7 - 2. Sun, J., Chen, S.Y., Qu, Y.P. and Li, J.F. (2015) Review on Stress Corrosion and Corrosion Fatigue Failure of Centrifugal Compressor Impeller. Chinese Journal of Mechanical Engineering, 28, 217-225.
https://doi.org/10.3901/CJME.2014.1210.178 - 3. 廖瑛, 梁加红, 姚新宇, 等. 实时仿真理论与支撑技术[M]. 长沙: 国防科技大学出版社, 2012.
- 4. 康凤举. 舰船仿真技术发展综述[J]. 舰船电子工程, 2004, 24(1): 9-11.
- 5. 陈华清, 敖晨阳. 舰船动力系统仿真中的柴油机数学模型[J]. 船舶工程, 2000, 22(5): 33-37.
- 6. 闫东, 梁前超, 等. 某型燃气轮机启动失败的模糊故障树分析[J]. 中国修船, 2015, 28(1): 40-42.
- 7. 向军, 许光, 杨叔华, 梁前超. 涡轮增压柴油机修后试验及性能仿真[J]. 内燃机与配件, 2016(10): 92-94.
- 8. Ding, J.M., Wang, Y.S., Ao, C.Y., et al. (2004) Mathematical Modeling and Simulation of Maneuvering for Waterjet-Propelled Catamarans. International Conference of Waterjet Propulsion 4, London: The Royal Institution of Naval Architects, 26-27 May 2004, 1-7.