Dynamical Systems and Control
Vol.
08
No.
03
(
2019
), Article ID:
31552
,
8
pages
10.12677/DSC.2019.83022
Qualitative Analysis of a Class of Cubic Polynomial Systems
Wenjing Ding1*, Guirong Pan2*, Wenya Jiang1
1School of Mathematics and Statistics, Linyi University, Linyi Shandong
2School of Information Science and Engineering, Linyi University, Linyi Shandong

Received: Jul. 6th, 2019; accepted: Jul. 16th, 2019; published: Jul. 31st, 2019

ABSTRACT
In this paper, the classical method of qualitative analysis is used to analyze the existence, type and local stability of a class of planar cubic polynomial differential system , . And the formal series method is used to determine the center-focus of the singular point. Finally, the conditions of the existence of limit cycles of the system are obtained by using the Hopf bifurcation method.
Keywords:Cubic Polynomial System, Singular Point, Limit Cycle, Hopf Bifurcation
一类三次多项式系统的定性分析
丁文静1*,潘桂荣2*,姜文雅1
1临沂大学数学与统计学院,山东 临沂
2临沂大学信息科学与工程学院,山东 临沂

收稿日期:2019年7月6日;录用日期:2019年7月16日;发布日期:2019年7月31日

摘 要
本文运用二维系统奇点的定性分析的经典方法对一类三次多项式微分系统 a3 y3+ a4 xy2, 进行了奇点存在性、类型和局部稳定性的详细分析,并运用形式级数判别法对原点进行了中心焦点的判定。最后,通过利用Hopf分支方法获得了系统存在极限环的条件。
关键词 :三次多项式系统,奇点,极限环,Hopf分支

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
在物理、化学、生物、医学、力学、工程技术以及管理科学等许多学科的众多研究领域及其应用问题的研究中,大量存在着各种具有复杂动力学行为的微分动力系统。在微分动力系统的模型建立以后,对系统定性性质与分支现象的研究将对现实系统存在的各种复杂现象从数学的角度来把握其规律性提供理论依据。在微分动力系统的研究中,两维的平面系统起到基础性的重要作用,在1881年,1882年,1885年,1886年,H. Poincaré连续在“微分方程定义的积分曲线”的标题下发表了四篇文章 [1] ,这批文章奠定了常微分方程定性理论的基础。而两维的平面多项式系统更是更加基础的研究领域。一直以来,从事微分方程研究的学者们在多项式系统的奇点存在性与类型分析,闭轨存在性、个数、稳定性,极限环个数与相关位置,奇闭轨的分支等等方面做了大量的工作并取得了丰富的结果。特别是自从H. Poincaré [2] 发现了极限环后,极限环论得到蓬勃发展。目前关于极限环的研究主要集中在极限环的存在性、稳定性、个数和它们的相对位置等问题,特别是在极限环的存在性方面已取得大量结果,至于个数和相对位置问题难度较大。著名数学家D. Hilbert [3] 在国际数学大会上提出了23个数学难题,其中第16个问题的后半部分就是:微
分方程 ( 是 的次数不超过n的实系数多项式)最多有几个极限环?相对位置如何?
关于这个问题法国数学家H. Dulac [4] 证明了上述方程极限环的个数是有限的。关于极限环论,我国许多数学家对平面二次系统极限环的存在性、唯一性、个数和相对位置做出许多突出贡献。史松龄 [5] 、王明淑和陈兰荪 [6] 举出了二次系统存在4个极限环的例子,破除了上界是3的传统猜测。叶彦谦先生给出了著名的叶彦谦分类将平面二次系统分为三类进行研究。对于第I类方程,叶彦谦 [7] 已经证明了在不同参数值下,恰有47种不同的全局结构图。而对于II类、III类方程情况复杂,暂时还未形成完整的结果。
对于平面三次多项式系统,由于种类繁多,研究起来会比较麻烦不易得到系统的结论,因此只是对特定的三次系统进行研究,目前已经有许多学者 [8] [9] [10] [11] [12] 对不同系数的三次系统进行研究。本文研究形如:
 (1)
(1)
的三次系统,其中 , , , , 均为实常数。从线性近似入手,通过不同系数的添加讨论系统(1)的奇点的存在性、奇点的局部稳定性和极限环的存在性。
2. 预备知识
2.1. 奇点定义 [13] [14]
给定平面系统 ,其中 , 在区域 上连续。若 满足 ,则称 是系统的奇点。
2.2. 奇点的类型 [13] [14]
对于平面线性系统
,其中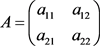 ,
,记
,
,于是特征方程为:
,特征根为:
。当
,
,记
,
,于是特征方程为:
,特征根为:
。当
时,根据A的特征根的不同情况其初等奇点可能出现四种类型:结点型、鞍点型、焦点型、中心型。当
时,结点和焦点是不稳定的;当 时,结点和焦点是稳定的。
时,结点和焦点是稳定的。
2.3. Hopf分支问题 [15] [16]
定理:考虑系统
(2)
其中P与Q是 的解析函数。设参数 时,系统(2)以 为中心型的稳定(不稳定)焦点。参数 时,系统(2)以 为不稳定(稳定)焦点,则对充分小的 ,系统(2)在点 附近至少有一个稳定(不稳定)的极限环。
3. 奇点分析
解方程组
(3)
得:1) 系统(1)有奇点 ;
2) 若 ,则系统(1)有奇点 , ,其中 ;
3) 若
,则系统(1)有奇点 ,
,其中
,
,
。
,
,其中
,
,
。
3.1. 奇点
对于奇点 ,其线性近似系统的系数矩阵为 ,特征方程为 λ2 − a1 λ +1 = 0 ,特征根 ,由此得如下定理:
定理1:1) 当 时 为系统(1)的稳定焦点, 时为不稳定焦点。
2) 当 时 为系统(1)的稳定结点, 时为不稳定结点。
3) 当 时 为系统(1)的中心型奇点(中心或者细焦点)。
3.2. 奇点
对于奇点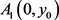 ,其线性近似系统的系数矩阵为
,特征方程为
,其特征根为:
,由此得如下定理:
,其线性近似系统的系数矩阵为
,特征方程为
,其特征根为:
,由此得如下定理:
定理2:1) 若 ,则有零特征根, 为系统(1)的高阶奇点。
2) 若 ,则特征根为异号实根, 为系统(1)的鞍点。
3) 若 ,则
i) 当 时特征根为同号实根, 为系统(1)的结点, 时不稳定, 时稳定。
ii) 当 时特征根为共轭复根, 为系统(1)的焦点, 时不稳定, 时稳定。 时 为系统(1)的中心型奇点(中心或者细焦点)。
3.3. 奇点
对于奇点 ,其线性近似系统的系数矩阵为 ,特征方程为 ,其特征根为: ,由此得如下定理:
定理3:1) 若
,则有零特征根, 为系统(1)的高阶奇点。
为系统(1)的高阶奇点。
2) 若 ,则特征根为异号实根, 为系统(1)的鞍点。
3) 若 ,则
i) 当 时特征根为同号实根, 为系统(1)的结点, 时不稳定, 时稳定。
ii) 当
时特征根为共轭复根,
为系统(1)的焦点,
时不稳定,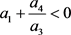 时稳定。
时
为系统(1)的中心型奇点(中心或者细焦点)。
时稳定。
时
为系统(1)的中心型奇点(中心或者细焦点)。
3.4. 奇点
对于 ,其线性近似系统的系数矩阵为 ,对应的特征方程为 ,特征根为 ,其中 , 。由此得如下定理:
定理4:1) 当 时有零特征根, 为系统(1)的高阶奇点。
2) 当 时, 为系统的鞍点。
3) 若 ,则
i) 当 时,特征根为同号实根, 为系统(1)的结点, 时不稳定, 时稳定。
ii) 若 时,特征根为共轭复根, 为系统(1)的焦点, 时不稳定, 时稳定。 时 为系统(1)的中心型奇点(中心或者细焦点)。
3.5. 奇点
对于 ,其线性近似系统的系数矩阵为 ,特征方程为 ,特征根 ,其中 , ,由此得如下定理:
定理5:1) 当 d4=0 时有零特征根, 为系统(1)的高阶奇点。
2) 当 时, 为系统的鞍点。
3) 若 ,则
i) 当 时,特征根为同号实根, 为系统(1)的结点, 时不稳定, 时稳定。
ii) 若
时,特征根为共轭复根, 为系统(1)的焦点,
时不稳定,
为系统(1)的焦点,
时不稳定, 时稳定。
时
为系统(1)的中心型奇点(中心或者细焦点)。
时稳定。
时
为系统(1)的中心型奇点(中心或者细焦点)。
3.6. 细焦点
我们仅对 点讨论。当 时,系统化为
(4)
定理6:1) 当 a4>0 时, 是系统(4)的一阶不稳定细焦点。
2) 当 时, 是系统(4)的一阶稳定细焦点。
3) 当 时, 为中心。
证明:利用形式级数判别法 [16] [17] 对(4)进行中心焦点的判定。令 ,其中 是x与y的k次齐次多项式,且 ,则:
(5)
令右端三次项为零,则有: ,将上式取极坐标 , 并消去 得:
(6)
因 ,故对(6)式两边进行积分得:
,即
令(5)式右端四次项为零,则有:
即 ,将上式取极坐标 , 并消去 得:
当 时, ,因此当 时, ,且 与 同号。
于是改取
满足方程
,其中
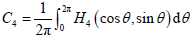 。
。
设 ,那么 ,进而有结论:
1) 当 时, 是系统(1)的不稳定细焦点。
2) 当 时, 是系统(1)的稳定细焦点。
当 时,因 , ,由对称原理得 为中心。
定理得证。
4. 极限环的存在性
定理7:下列条件之一成立时,系统(1)在奇点外至少存在一个极限环,且当 时所产生的极限环不稳定,当 时所产生的极限环稳定。
1) , 且 ;
2) , 。
证明:当 , 时, 为不稳定的细焦点,而当 时系统(1)以 为稳定焦点。由Hopf分支问题的Liapunov第二方法 [17] [18] 可知在条件(1)下,系统(1)在奇点 外至少产生一个不稳定极限环。
当 , 时 为稳定的细焦点,而当 时系统(1)以 为不稳定焦点。由Hopf分支问题的Liapunov第二方法可知在条件(2)下,系统(1)在奇点外至少产生一个稳定极限环。
定理得证。
基金项目
山东省自然科学基金(ZR2018MA016,ZR2015AL005),山东省软科学研究计划项目(2012RKA13021)。
文章引用
丁文静,潘桂荣,姜文雅. 一类三次多项式系统的定性分析
Qualitative Analysis of a Class of Cubic Polynomial Systems[J]. 动力系统与控制, 2019, 08(03): 205-212. https://doi.org/10.12677/DSC.2019.83022
参考文献
- 1. 秦元勋. 学习H. Poincare的数学工作思想方法[J]. 西北大学学报, 1982(1): 1-7.
- 2. Poincaré, H. (1881) Mémoire sur les courbes définie par une équation differentielle. Journal de mathématiques pures et appliquées, 7, 375-422.
- 3. Hilbert, D. (1901) Mathematische Probleme. Archiv der Mathematik und Physik, 1, 44-63, 213-237.
- 4. Dulac, H. (1923) Sur les Cycles Limites. Bulletin de la Société Mathématique de France, 51, 45-188.
https://doi.org/10.24033/bsmf.1031 - 5. 史松龄. 二次系统(E2)出现至少四个极限环的例子[J]. 中国科学, 1979(11): 1051-1056.
- 6. 陈兰荪, 王明淑. 二次系统极限环的相对位置与个数[J]. 数学学报, 1979, 22(6): 751-758.
- 7. 叶彦谦. 极限环论[M]. 上海: 上海科学技术出版社, 1984.
- 8. 叶彦谦. 多项式微分系统定性理论[M]. 上海: 上海科学技术出版, 1995.
- 9. 卜令杰, 窦霁虹, 刘萌萌, 等. 一类三次系统极限环的存在唯一性[J]. 延安大学学报(自然科学版), 2014, 33(2): 1-5.
- 10. 朱科科. 一类三次系统极限环的存在性[J]. 安阳师范学院学报, 2017(5): 4-8.
- 11. 马知恩. 一类三次系统极限环的存在唯一性[J]. 数学年刊A辑(中文版), 1999, 19(1): 16-18.
- 12. 周久红. 一类三次系统的定性分析[D]: [硕士学位论文]. 合肥: 安徽大学, 2013.
- 13. 东北师范大学微分方程教研室. 常微分方程[M]. 北京: 高等教育出版社, 2005.
- 14. 丁同仁, 李承治. 常微分方程教程[M]. 第2版. 北京: 高等教育出版社, 2004.
- 15. 张锦炎. 常微分方程几何理论与分支问题[M]. 北京: 北京大学出版社, 1981.
- 16. 罗定军, 张祥, 董梅芳. 动力系统的定性与分支理论[M]. 北京: 科学出版社, 2001.
- 17. 张芷芬, 丁同仁, 黄文灶, 董镇喜. 微分方程定性理论[M]. 北京: 科学出版社, 1985.
- 18. Luo, D., Wang, X., Zhu, D. and Han, M. (1997) Bifurcation Theory and Methods of Dynamical Systems. In: Advanced Series in Dynamical Systems, vol. 15, World Scientific, Singapore.
https://doi.org/10.1142/2598