Dynamical Systems and Control
Vol.
11
No.
01
(
2022
), Article ID:
48426
,
8
pages
10.12677/DSC.2022.111003
分数阶系统的鲁棒稳定性研究
郭校中
西安电子科技大学,陕西 西安
收稿日期:2022年1月1日;录用日期:2022年1月14日;发布日期:2022年1月28日

摘要
本文将针对分数阶( )系统,同时考虑最常见的两种不确定类型,即多胞不确定和无穷范数。首先,给出了不确定分数阶系统无状态反馈时鲁棒稳定性条件。其次,采用线性矩阵不等式的形式给出了不确定分数阶系统状态反馈控制器的设计方法。最后,通过两个数值算例验证了理论的正确性。
关键词
分数阶系统,多胞不确定,范数有界不确定,鲁棒稳定性

Study on the Robust Stability of Fractional-Order System
Xiaozhong Guo
Xidian University, Xi’an Shaanxi
Received: Jan. 1st, 2022; accepted: Jan. 14th, 2022; published: Jan. 28th, 2022

ABSTRACT
In this paper, we will consider the two most common types of uncertainty for fractional-order systems, which are subjected to poly-topic and H-infinity bounded uncertainties with . Firstly, the robust stability conditions of uncertain fractional-order systems without state feedback are given. Secondly, the design method of state feedback controller for the fractional system with uncertainty is given in the form of linear matrix inequality. Finally, two numerical examples are given to verify the correctness of the theory.
Keywords:Fractional-Order System, Poly-Topic Uncertainty, Norm Bounded Uncertainty, Robust Stability

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
不确定性研究有多种形式。在 [1] [2] 中,分数阶微积分作为整数阶微积分的推广和延伸,由于可以更好地刻画函数的历史发展过程,有更强的记忆性和全局相关性,得到了国内外学者的广泛关注,利用多胞和范数有界描述不确定性,给出了一个基于线性矩阵不等式稳定性分析和控制器设计的充分条件。在 [3] 中,考虑了区间不确定性下的分数阶系统的鲁棒稳定性,分数阶与其他模型参数之间存在确定的线性耦合关系。在 [4] 中,分数阶的研究在控制领域中主要集中于物理对象的建模。 [5] [6] 中,基于线性矩阵不等式分别对 和 的情况,给出了具有区间不确定性的分数阶系统稳定的充要条件。在 [7] 中,同时考虑了多胞和二范数有界不确定性。在 [8] 中,研究了在多胞和范数有界不确定条件下的分数阶系统的稳定性和镇定问题。在 [9] 中,研究了不确定分数阶的鲁棒稳定界问题,并且系统具有范数有界不确定性。文献 [10] [11] [12] [13] 研究不确定性矩阵谱范数的上界,考虑的稳定区域要么是复平面的左半平面,要么是单一的关于实轴对称的凸域。这些上界都是基于Lyapunov定理。文献 [14] 考虑了当分数阶系统具有多胞型不确定时的鲁棒镇定控制器的设计方法。
在 [15] 中,作者从控制输入能效的角度研究了分数阶控制系统,给出了控制输入能量函数的发散条件,对作用于对象上的控制器能量优化起到了作用。
基于上述研究,本文将研究两种不确定性与稳定性之间的关系,推导出了分数阶( )系统在多胞和范数有界不确定情况下,系统的稳定性条件。设计状态反馈控制器使分数阶系统变得稳定,并通过数值算例,验证理论的正确性。
2. 预备知识
在本文的后续中,如果没有特别强调或指出,一般符号的含义如下所示。
表示矩阵X的转置, 表示矩阵X的共轭转置, 表示X是正定矩阵。
等于 ,矩阵中的 表示这是对称矩阵中的对称部分。 表示矩阵的Kronecker积。 是 阶Caputo微分算子。
是X的无穷大范数, 是n阶单位矩阵。
引理1. 当 时,系统稳定的充分必要条件是存在正定矩阵 , 使得如下线性矩阵不等式成立:
(1)
其中 表示矩阵的Kronecker积:
, (2)
引理2. 对于具有适当维数的正定矩阵 和矩阵 ,有以下不等式成立:
(3)
引理3. 对于给定的对称矩阵:
(4)
都具有恰当的维数,则以下三个条件是等价的:
1. ;
2. , ;
3. , ;
引理4. 当 时,分数阶系统渐近稳定的充分必要条件是:
(5)
其中 是辐角函数, 是矩阵A的所有特征值。
3. 结果与分析
3.1. 鲁棒稳定性分析
定理3.1 当 时,多胞和范数有界不确定分数阶系统具有鲁棒渐近稳定性的充分条件是:存在矩阵 ,,, 满足约束:
(6)
证明. 根据引理1,如果存在正定矩阵 及 ,使得分数阶系统渐近稳定,那么则有:
(7)
根据引理2,存在矩阵 ,
,,,,
且有 ,可以得到:
(8)
使用引理3,可以将式(8)写为:
, (9)
根据引理1,系统的鲁棒稳定性得证。
3.2. 状态反馈控制器设计
定理3.2 当 时,多胞和范数有界不确定分数阶系统具有鲁棒渐近稳定性的充分条件是:存在矩阵 ,,,, 满足约束:
(10)
式中状态反馈器可描述为:
,
证明. 根据引理1,如果存在正定矩阵 , 及 , 使得分数阶系统渐近稳定,那么则有:
(11)
根据引理2,存在矩阵 ,,,,,且有 ,, 可以推导出:
(12)
使用引理3,可以将式(12)写为:
,
(13)
根据引理1,系统的鲁棒稳定性得证。
4. 数值仿真
在本节中,通过两个数值示例来证明上述理论的正确性,由于分数阶微分不能直接仿真,因此使用 [11] 中提出的改进的Oustaloup方法进行了以下仿真。在第一个示例中研究了不确定分数阶系统的稳定性问题,在第二个实例中,设计状态反馈器,使得系统稳定。
4.1. 示例1
考虑具有多胞和范数有界不确定性系统的鲁棒稳定性问题,其中系统参数给出如下:
,
根据定理3.1,使用MATLB提供的LMI工具箱,得到LMI式(6)的解:
,
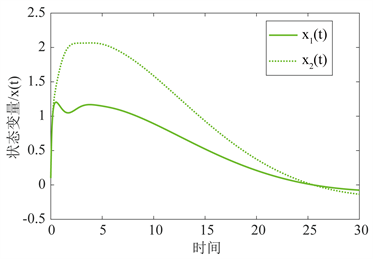
当 ; 时,给系统加入不确定参数,随机选取不确定参数的值,由图1可以看出随着最大不确定性界 的增加,不确定性因素的影响也会增加,系统的输出响应也将由收敛变的发散。这与定理3.1相一致。
4.2. 示例2
考虑具有多胞和范数有界不确定性系统的鲁棒稳定性问题,其中系统参数给出如下:
,
 (a)
(b)
(a)
(b)
 (c)
(c)
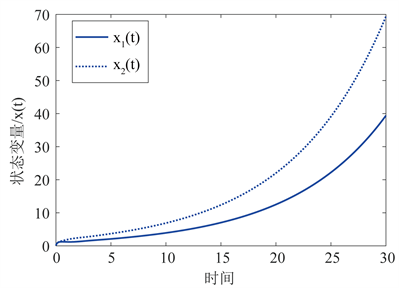
Figure 1. Output response of the system at different uncertainty bounds
图1. 系统在不同不确定界值时的输出响应
根据定理3.2,使用MATLB提供的LMI工具箱,得到LMI式(10)的解:
,,
,
该系统中,当系统的控制输入 ,系统不是渐近稳定的,由图2系统的时间响应可以得出,原系统的状态是发散的。
根据定理3.2,为了保证系统的稳定性,加入状态反馈控制器 使得系统渐近稳定,随机选取系统的加权系数 ; ,系统不确定参数的无穷大范数 ,求解出控制器的增益 。由图3系统的时间响应可以看出,系统时间响应由图2的发散状态最终变了收敛状态从而说明了定理3.2的正确性。
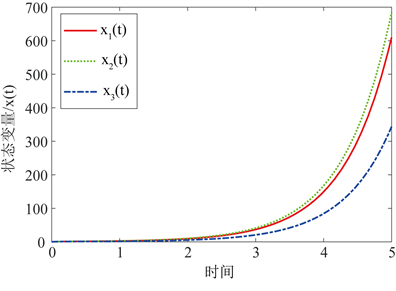
Figure 2. Eigenvalues and time responses of the system
图2. 系统的特征值和时间响应

Figure 3. Eigenvalues and time responses of the system
图3. 系统的特征值和时间响应
5. 结论
本文推导了在 时,多胞和无穷范数有界不确定分数阶系统的鲁棒稳定性的充分条件。在不满足鲁棒稳定条件时,设计了相应的线性状态反馈稳定控制器。最后,通过两个数值例子验证了理论的正确性。所有的结果都是根据MATLAB提供的LMI计算得出。仿真结果表明随着不确定性无穷范数的增大,其对系统的稳定性影响逐步增大,系统逐渐失稳。但是对于具体的系统,其无穷范数的上界到底如何确定,这也是后续需要进行进一步研究的问题。同时基于该方法设计的状态反馈控制器可以有效镇定不确定分数阶系统,且控制代价小,适合于工程实现。
文章引用
郭校中. 分数阶系统的鲁棒稳定性研究
Study on the Robust Stability of Fractional-Order System[J]. 动力系统与控制, 2022, 11(01): 19-26. https://doi.org/10.12677/DSC.2022.111003
参考文献
- 1. Dong, J. and Yang, G.H. (2013) Robust Static Output Feedback Control Synthesis for Linear Continuous Systems with Poly-Topic Uncertainties. Automatica, 49, 1821-1829.
https://doi.org/10.1016/j.automatica.2013.02.047 - 2. Jiang, J., Li, T.J., Mei, Y.J., and Wang, H.J. (2016) Passive Intermodulation Analysis of Coupled Electro-Thermal Microwave Loads. Journal of Xidian University, 43, 179-184.
- 3. Liao, Z., Peng, C., Li, W. and Wang, Y. (2011) Robust Stability Analysis for a Class of Fractional Order Systems with Uncertain Parameters. Journal of the Franklin Institute, 348, 1101-1113.
https://doi.org/10.1016/j.jfranklin.2011.04.012 - 4. Chen, G., Xiao, M. and Wan, Y.H. (2021) Propagation Dynamics of Fractional Order Delay Epidemic Model. Control Theory & Applications, 38, 1257-1264.
- 5. Lu, J.G. and Chen, G. (2009) Robust Stability and Stabilization of Fractional-Order Interval Systems with the Fractional Order: The 0 < a < 1 Case. IEEE Transactions on Automatic Control, 55, 152-158.
https://doi.org/10.1109/TAC.2009.2033738 - 6. Adelipour, S., Abooee, A. and Haeri, M. (2014) LMI-Based Sufficient Conditions for Robust Stability and Stabilization of LTI-Fractional-Order Systems Subjected to Interval and Poly-Topic Uncertainties. Transactions of the Institute of Measurement and Control, 37, 1207-1216.
https://doi.org/10.1177/0142331214559120 - 7. Li, S.L. (2018) LMI Stability Conditions and Stabilization of Fractional-Order Systems with Poly-Topic and Two-Norm Bounded Uncertainties for Fractional-Order α: The 1 < α< 2 Case. Computational and Applied Mathematics, 37, 5000-5012.
https://doi.org/10.1007/s40314-018-0610-x - 8. Lu, J.G., Ma, Y.D. and Chen, W. (2013) Maximal Perturbation Bounds for Robust Stabilizability of Fractional-Order Systems with Norm Bounded Perturbations. Journal of the Franklin Institute, 350, 3365-3383.
https://doi.org/10.1016/j.jfranklin.2013.07.014 - 9. Yang, Z.C., Zheng, S.Q., Liu, F. and Xie, Y.L. (2020) Adaptive Output Feedback Control for Fractional Order Multi-Agent Systems. ISA Transactions, 96, 195-209.
https://doi.org/10.1016/j.isatra.2019.07.008 - 10. Patel, R.V. and Toda, M. (1980) Quantitative Measures of Robustness for Multi-Variable System. Proceedings of Automatic Control Conference, San Francisco, 13-15 August 1980, 437-442.
- 11. Gardiner, J.D. (1997) Computation of Stability Bounds for State Space Models with Structured Uncertainty. IEEE Transactions on Automatic Control, 42, 253-256.
https://doi.org/10.1109/9.554405 - 12. Yedavalli, R.K. (1993) Robust Root Clustering for Linear Uncertain System Using Generalized Lyapunov Theory. Automatica, 29, 237-240.
https://doi.org/10.1016/0005-1098(93)90188-Y - 13. Juang, Y.T. (1991) Robust Stability and Robust Pole-Assignment of Linear System with Structured. IEEE Transactions on Automatic Control, 36, 635-637.
https://doi.org/10.1109/9.76373 - 14. Luo, S.Y. and Lu, J.G. (2021) Robust Stability and Stabilization of Fractional-Order Systems with Poly-Topic Uncertainties via Homogeneous Polynomial Parameter-Dependent Matrix Forms. International Journal of General Systems, 50, 891-914.
https://doi.org/10.1080/03081079.2021.1976774 - 15. Boyd, S., Ghaouli, L., Feron, E. and Balakrishnan, V. (1994) Linear Matrix Inequalities in System and Control Theory. SIAM, Philadelphia, 7-41.
https://doi.org/10.1137/1.9781611970777