DoS攻击下不确定网络控制系统基于事件触发机制的鲁棒有限时间可靠控制 Robust Finite-Time Reliable Control for Uncertain Networked Control Systems under Denial of Service Attacks Based on Event Triggering Mechanism

doi:10.12677/DSC.2022.113012

Dynamical Systems and Control
Vol. 11 No. 03 ( 2022 ), Article ID: 53437 , 13 pages
10.12677/DSC.2022.113012

DoS攻击下不确定网络控制系统基于事件触发机制的鲁棒有限时间可靠控制

薛梦洁，王为群，李天瑞

●How to Cite this Article

南京理工大学数学与统计学院，江苏南京

收稿日期：2022年6月16日；录用日期：2022年6月28日；发布日期：2022年7月8日

摘要

本文研究了在执行器故障和非周期拒绝服务(Denial of Service, DoS)攻击下不确定网络控制系统(Networked Control Systems, NCSs)基于事件触发机制的鲁棒有限时间稳定性。首先，基于离散事件触发通信方案，提出了一种类似切换的时滞系统模型。然后，通过构造分段Lyapunov-Krasovskii泛函，导出了保证系统有限时间稳定性的充分条件，并以线性矩阵不等式形式表示。此外，给出了鲁棒可靠控制器与事件触发参数的联合设计。最后，通过两个数值算例验证了提出方法的有效性。

关键词

网络控制系统，可靠控制，事件触发，有限时间，拒绝服务攻击

Robust Finite-Time Reliable Control for Uncertain Networked Control Systems under Denial of Service Attacks Based on Event Triggering Mechanism

Mengjie Xue, Weiqun Wang, Tianrui Li

School of Mathematics and Statistics, Nanjing University of Science and Technology, Nanjing Jiangsu

Received: Jun. 16^th, 2022; accepted: Jun. 28^th, 2022; published: Jul. 8^th, 2022

ABSTRACT

In this paper, robust finite-time stability of Networked Control Systems (NCSs) based on event triggering mechanism under actuator failures and non-periodic Denial of Service (DoS) attacks is investigated. First, a switching-like delay system model is presented under discrete event-triggered communication scheme. Then, by constructing piecewise Lyapunov-Krasovskii functional, sufficient conditions for finite-time stability of the system are derived and expressed with a set of linear matrix inequalities. Moreover, the co-design of the robust reliable controller and the event-triggered parameter is obtained. Finally, two examples are employed to demonstrate the effectiveness of the proposed method.

Keywords:Networked Control Systems, Reliable Control, Event-Triggered, Finite-Time, Denial of Service Attacks

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

随着计算机网络技术的快速发展，网络控制系统受到了广泛的关注 [1]。网络控制系统是指传感器、控制器和执行器通过通信网络连接的控制系统，具有成本低、灵活性高、安装简单等优点。但是网络的接入不可避免地带来一些问题，比如网络拥塞、网络时滞以及网络攻击等。为了避免网络拥塞，实现通信资源的高效利用，事件触发方案被广泛采用，它能有效减少不必要的数据传输。一般来说，事件触发方案可以分为连续事件触发 [2] 和离散事件触发 [3]。前者的触发条件依赖于对系统状态的连续监控，而后者只需要周期性地验证事件触发条件。

网络攻击可以分为DoS攻击 [4]、欺骗性攻击 [5]、重放攻击 [6]，其中DoS攻击会中断数据传输，严重降低系统性能，引起了很多学者的关注。例如， [7] 研究了DoS攻击下不确定网络控制系统基于事件触发机制的鲁棒镇定问题，这里考虑的是周期性DoS攻击。然而，假设DoS攻击周期性地进行是有局限性的，现实中更多的攻击是非周期的。 [8] 进一步考虑了非周期DoS攻击下网络控制系统的指数稳定性问题。另外，由于元器件老化、外界干扰等因素，执行器容易发生故障。因此，需要设计一个可靠的控制器，能够容忍控制组件故障和DoS攻击的影响。

对于网络控制系统，大多文献考虑的都是渐近稳定性或者是指数稳定性，它们都定义在一个无限的时间间隔内。在实际应用中，有限时间间隔内稳定性也有广泛应用 [9]。为此，文献 [10] 提出了有限时间稳定性的概念。近年来，网络控制系统的有限时间稳定性受到了一些关注。文献 [11] 研究了网络控制系统的有限时间有界性问题。然而，在控制器设计中没有考虑到网络攻击的影响。在 [12] 中，作者考虑了受欺骗性攻击的网络系统基于事件触发机制的有限时间控制问题。

目前有限时间意义下受DoS攻击的网络控制系统的事件触发控制研究还比较少。为此，本文研究非周期DoS攻击下的不确定网络控制系统基于事件触发机制的鲁棒有限时间可靠控制问题。

2. 问题描述

考虑如下不确定网络控制系统

$\dot{x} (t) = (A + Δ A (t)) x (t) + (B + Δ B (t)) u^{f} (t),$ (1)

其中 $x (t) \in R^{n}$ ， $u^{f} (t) \in R^{m}$ 分别为系统状态和带有执行器故障的控制输入。 $A, B$ 为适当维数的实矩阵。 $Δ A (t), Δ B (t)$ 为未知的系统时变不确定性的矩阵，满足

$Δ A (t) = E H (t) F_{1}, Δ B (t) = E H (t) F_{2},$ (2)

其中 $E, F_{1}, F_{2}$ 为已知的实矩阵， $H (t)$ 为未知的时变矩阵且满足 $H^{T} (t) H (t) \leq I$ 。

在实际应用中，由于元器件或环境因素，执行器会发生故障。考虑如下形式的控制输入

$u^{f} (t) = Ξ u (t),$ (3)

其中 $Ξ$ 为执行器故障矩阵，具有如下形式

$Ξ = d i a g {d_{1}, d_{2}, \dots, d_{m}},$

其中 $0 \leq \underline{d_{i}} \leq d_{i} \leq \bar{d_{i}} \leq 1, i = 1, 2, \dots, m$ ， $\underline{d_{i}}$ 和 $\bar{d_{i}}$ 是正常数。为了便于分析，引入以下符号

$U = d i a g {u_{1}, u_{2}, \dots, u_{m}}, L = d i a g {p_{1}, p_{2}, \dots, p_{m}}, E = d i a g {e_{1}, e_{2}, \dots, e_{m}}$

其中 $u_{i} = \frac{\underline{d_{i}} + \bar{d_{i}}}{2}$ ， $p_{i} = \frac{\bar{d_{i}} - \underline{d_{i}}}{\underline{d_{i}} + \bar{d_{i}}}$ ， $e_{i} = \frac{d_{i} - u_{i}}{u_{i}}$ 。则故障矩阵可以改写成如下形式

$Ξ = U (I + E), | E | \leq L \leq I,$ (4)

其中 $| E | = d i a g {| e_{1} |, | e_{2} |, \dots, | e_{m} |}$ 。

本文考虑如下非周期DoS攻击信号 [13]

$I_{D O S} (t) = {\begin{cases} 0, t \in [h_{n}, h_{n} + l_{n}) \\ 1, t \in [h_{n} + l_{n}, h_{n + 1}) . \end{cases}$ (5)

其中 $h_{n} + l_{n}$ 表示第 $(n + 1)$ 个DoS区间的开始， $h_{n + 1} - h_{n} - l_{n}$ 表示第 $(n + 1)$ 个DoS信号持续时间。记 $H_{n} = {h_{n} + l_{n}} \cup [h_{n} + l_{n}, h_{n + 1})$ ， ${H_{n}}_{n \in ℕ}$ 满足 $0 = h_{0} < h_{0} + l_{0} < h_{1} < h_{1} + l_{1} < h_{2} < \dots$ 。

假设 [8] 存在两个正标量 $l_{\min}$ ， $b_{\max}$ 满足 $l_{\min} \leq \inf_{n \in N} {l_{n}}$ 和 $\sup_{n \in N} {h_{n} - h_{n - 1} - l_{n - 1}} \leq b_{\max}$ 。

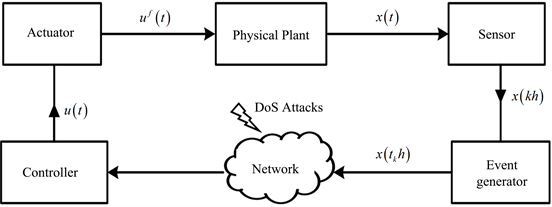
Figure 1. Structure diagram of NCSs based on event triggering mechanism

图1. 基于事件触发机制的网络控制系统结构示意图

如图1所示，本文考虑的传感器是时间触发的，采样周期为h，执行器是事件触发的。基于事件触发机制的控制为

$u (t) = K x (t_{k} h), t \in [t_{k} h, t_{k + 1} h),$ (6)

其中 $t_{k} h$ 表示最新的触发时刻， $t_{k + 1} h$ 是下一次触发时刻，这里我们先假设在区间 $[t_{k} h, t_{k + 1} h)$ 上没有DoS攻击。

选取如下事件触发方案

$e_{k, j}^{T} (t_{k_{j}} h) Φ e_{k, j} (t_{k_{j}} h) \geq δ x^{T} (t_{k} h) Φ x (t_{k} h),$ (7)

其中 $e_{k, j} (t_{k_{j}} h) = x (t_{k_{j}} h) - x (t_{k} h)$ ， $t_{k_{j}} h = t_{k} h + j h (k, j \in N)$ 表示两次触发之间的采样时刻， $t_{k} h$ 为最新的事件触发时刻， $δ \in (0, 1)$ 为事件触发阈值， $Φ$ 是待设计的正定加权矩阵。记 $L_{1, n} = [h_{n}, h_{n} + l_{n})$ ， $L_{2, n} = [h_{n} + l_{n}, h_{n + 1})$ ，在DoS攻击(5)下，事件触发时刻序列由下式确定

$t_{k, n} h = {t_{k_{j}} h 满足 (7) | t_{k_{j}} h \in L_{1, n - 1}} \cup {h_{n}},$ (8)

其中 $n, k_{j}, j \in N$ ，k是第n个DoS攻击区间事件触发的次数。记 $ν_{k, n} = [t_{k, n} h, t_{k + 1, n} h)$ ，DoS攻击(5)下控制输入 $u (t)$ 可以写成如下形式

$u (t) = {\begin{cases} K x (t_{k, n} h), t \in [t_{k, n} h, t_{k + 1, n} h) \cap L_{1, n - 1} \\ 0, t \in L_{2, n - 1}, \end{cases}$ (9)

其中序列 ${t_{k, n} h}$ ( $t_{0, n} ≜ h_{n - 1}$ )表示第n个DoS攻击区间内的控制更新时刻， $k \in {0, 1, \dots, k (n)} ≜ κ (n)$ ， $k (n) = \sup {k \in N | t_{k, n} h \leq h_{n - 1} + l_{n - 1}}$ ， $n \in N$ 。

将(9)代入(1)可得

$\dot{x} (t) = {\begin{cases} (A + Δ A (t)) x (t) + (B + Δ B (t)) Ξ K x (t_{k, n} h), t \in ν_{k, n} \cap L_{1, n - 1} \\ (A + Δ A (t)) x (t), t \in L_{2, n - 1} . \end{cases}$ (10)

为了便于分析，将 $ν_{k, n} (\forall k \in κ (n), n \in ℕ)$ 分成类似采样的子区间，即

$ν_{k, n} = \cup_{l = 1}^{λ_{k, n} + 1} F_{k, n}^{l},$ (11)

其中

$F_{k, n}^{l} = [t_{k, n} h + (l - 1) h, t_{k, n} h + l h), l = 1, 2, \dots, λ_{k, n},$

$λ_{k, n} ≜ \sup {l \in ℕ | t_{k, n} h + l h < t_{k + 1, n} h},$

$F_{k, n}^{λ_{k, n} + 1} = [t_{k, n} h + λ_{k, n} h, t_{k + 1, n} h) .$

因为

$L_{1, n - 1} \subseteq \cup_{k = 0}^{k (n)} ν_{k, n},$ (12)

结合式(11)，(12)，可得

$L_{1, n - 1} = \cup_{k = 0}^{k (n)} {υ_{k, n} \cap L_{1, n - 1}} = \cup_{k = 0}^{k (n)} \cup_{l = 1}^{λ_{k, n} + 1} {F_{k, n}^{l} \cap L_{1, n - 1}} .$

记 $ϕ_{k, n}^{l} = F_{k, n}^{l} \cap L_{1, n - 1}$ ，则 $L_{1, n - 1} = \cup_{k = 0}^{k (n)} \cup_{l = 1}^{λ_{k, n} + 1} ϕ_{k, n}^{l}$ 。

定义

$τ_{k, n} (t) = {\begin{cases} t - t_{k, n} h, t \in ϕ_{k, n}^{1} \\ t - t_{k, n} h - h, t \in ϕ_{k, n}^{2} \\ ⋮ \\ t - t_{k, n} h - λ_{k, n} h, t \in ϕ_{k, n}^{λ_{k, n} + 1}, \end{cases}$

$e_{k, n} (t) = {\begin{cases} 0, t \in ϕ_{k, n}^{1} \\ x (t_{k, n} h) - x (t_{k, n} h + h), t \in ϕ_{k, n}^{2} \\ ⋮ \\ x (t_{k, n} h) - x (t_{k, n} h + λ_{k, n} h), t \in ϕ_{k, n}^{λ_{k, n} + 1}, \end{cases}$

可得 $τ_{k, n} (t) \in [0, h)$ ， $t \in ν_{k, n} \cap L_{1, n - 1}$ ，进而有

$x (t_{k, n} h) = x (t - τ_{k, n} (t)) + e_{k, n} (t), t \in ν_{n, k} \cap L_{1, n - 1} .$ (13)

将(13)代入(10)可得如下类似切换的时滞系统

${\begin{cases} \dot{x} (t) = {\begin{cases} (A + Δ A (t)) x (t) + (B + Δ B (t)) Ξ K x (t - τ_{k, n} (t)) + (B + Δ B (t)) Ξ K e_{k, n} (t), t \in ν_{k, n} \cap L_{1, n - 1} \\ (A + Δ A (t)) x (t), t \in L_{2, n - 1} \end{cases} \\ x (t) = ϕ (t), t \in [- h, 0], \end{cases}$ (14)

其中 $ϕ (t)$ 是状态 $x (t)$ 在区间 $[- h, 0]$ 的初始条件。

本文的控制目标是联合设计事件触发参数 $Φ$ 以及基于事件的状态反馈控制器增益K使类似切换的时滞系统(14)在DoS攻击(5)的影响下是鲁棒有限时间稳定的。下面，我们引入一些定义和引理，以方便推导主要结果。

定义1. [14] (DoS攻击频率)存在 $ν_{1} \geq 0$ 和 $τ_{D} \geq h$ 使得 $n (t) \leq v_{1} + \frac{t}{τ_{D}}$ ，其中 $n (t)$ 表示在 $[0, t)$ 区间内发生的DoS攻击次数。

定义2. 给定三个正数 $c_{1}, c_{2}, T_{f}$ ，满足 $c_{1} < c_{2}$ ，一个正定矩阵R，如果

$\sup_{θ \in [- h, 0]} {x^{T} (θ) R x (θ), {\dot{x}}^{T} (θ) R \dot{x} (θ)} \leq c_{1} \Rightarrow x^{T} (t) R x (t) < c_{2}, \forall t \in [0, T_{f}],$

则系统(14)是关于 $(c_{1}, c_{2}, T_{f}, R)$ 鲁棒有限时间稳定的。

引理1. [15] 对于满足条件 $0 \leq τ (t) \leq τ_{M}$ 的连续函数 $τ (t)$ ，以及向量函数 $x (t) : [- τ_{M}, 0) \to R^{n}$ ，对任意的正定堆成矩阵Q和实矩阵U，满足条件 $[\begin{matrix} Q & U \\ * & Q \end{matrix}] \geq 0$ ，那么有下面的不等式成立

$- τ_{M} \int_{t - τ_{M}}^{t} {\dot{x}}^{T} (s) Q \dot{x} (s) d s \leq {[\begin{matrix} x^{T} (t) \\ x^{T} (t - τ (t)) \\ x^{T} (t - τ_{M}) \end{matrix}]}^{T} [\begin{matrix} - Q & Q - U & - U \\ * & - 2 Q + U + U^{T} & Q - U \\ * & * & - Q \end{matrix}] [\begin{matrix} x (t) \\ x (t - τ (t)) \\ x (t - τ_{M}) \end{matrix}] .$

引理2. [16] 令 $U, V, W$ 和X是具有合适维数的实矩阵，且满足 $X = X^{T}$ ， $V^{T} V \leq I$ ，则

$X + U V W + W^{T} V^{T} U^{T} < 0,$

当且仅当存在 $ρ > 0$ 使得

$X + ρ U U^{T} + ρ^{- 1} W^{T} W < 0.$

引理3. [17] 对于矩阵 $R > 0$ ，X以及任意标量 $ε$ ，不等式 $- X R^{- 1} X \leq ε^{2} R - 2 ε X$ 成立。

3. 主要结果

先考虑不确定定项 $Δ A (t) = Δ B (t) = 0$ ，有如下系统

${\begin{cases} \dot{x} (t) = {\begin{cases} A x (t) + B Ξ K x (t - τ_{k, n} (t)) + B Ξ K e_{k, n} (t), t \in ν_{k, n} \cap L_{1, n - 1} \\ A x (t), t \in L_{2, n - 1} \end{cases} \\ x (t) = φ (t), t \in [- h, 0] . \end{cases}$ (15)

3.1. 有限时间稳定性分析

对于类似切换的系统(15)，本文选取如下Lyapunov-Krasovskii泛函

$V (t) = {\begin{cases} V_{1} (t), t \in ν_{k, n} \cap L_{1, n - 1} \\ V_{2} (t), t \in L_{2, n - 1}, \end{cases}$

其中 $V_{i} (t) = x^{T} (t) P_{i} x (t) + \int_{t - h}^{t} x^{T} (s) e^{{(- 1)}^{i} α_{i} (t - s)} Q_{i} x (s) d s + h \int_{- h}^{0} \int_{t + θ}^{t} {\dot{x}}^{T} (s) e^{{(- 1)}^{i} α_{i} (t - s)} Z_{i} \dot{x} (s) d s d θ$ 。

下面的定理估计了所选定的Lyapunov-Krasovskii泛函的上界。

定理1. 给定DoS攻击参数 $υ_{1} \geq 0$ ， $τ_{D} \geq h$ ，反馈增益矩阵K，正定矩阵R。令 $P_{i} = R^{\frac{1}{2}} {\tilde{P}}_{i} R^{\frac{1}{2}}$ ， $Q_{i} = R^{\frac{1}{2}} {\tilde{Q}}_{i} R^{\frac{1}{2}}$ ， $Z_{i} = R^{\frac{1}{2}} {\tilde{Z}}_{i} R^{\frac{1}{2}}$ ， $i \in {1, 2}$ ，如果对于给定常数 $α_{i} > 0$ ， $0 < δ < 1$ ， $ρ > 0$ ，存在矩阵 $P_{i} > 0$ ， $Φ > 0$ ， $Q_{i} > 0$ ， $Z_{i} > 0$ ，S，使得

$Π_{1} < 0, Σ_{1} > 0,$ (16)

$Π_{2} < 0, Σ_{2} > 0,$ (17)

其中

$Σ_{1} = [\begin{matrix} Z_{1} & S_{1} \\ * & Z_{1} \end{matrix}], Σ_{2} = [\begin{matrix} Z_{2} & S_{2} \\ * & Z_{2} \end{matrix}], Π_{1} = [\begin{matrix} \tilde{ϒ} & φ & ψ \\ * & - ρ^{- 1} I & 0 \\ * & 0 & - ρ I \end{matrix}], \tilde{ϒ} = [\begin{matrix} \tilde{Θ} & h {\tilde{Γ}}_{1}^{T} Z_{1} \\ * & - Z_{1} \end{matrix}], {\tilde{Γ}}_{1}^{T} = [\begin{matrix} A^{T} \\ {(B U K)}^{T} \\ 0 \\ {(B U K)}^{T} \end{matrix}],$

$φ = [\begin{matrix} P_{1} B \\ 0 \\ 0 \\ \begin{array}{l} 0 \\ h Z_{1} B \end{array} \end{matrix}], ψ = [\begin{matrix} 0 \\ K^{T} U^{T} \\ 0 \\ \begin{array}{l} K^{T} U^{T} \\ 0 \end{array} \end{matrix}], \tilde{Θ} = [\begin{matrix} {\tilde{Θ}}_{11} & {\tilde{Θ}}_{12} & {\tilde{Θ}}_{13} & {\tilde{Θ}}_{14} \\ * & {\tilde{Θ}}_{22} & {\tilde{Θ}}_{23} & {\tilde{Θ}}_{24} \\ * & * & {\tilde{Θ}}_{33} & 0 \\ * & * & * & {\tilde{Θ}}_{44} \end{matrix}], Π_{2} = [\begin{matrix} Ω_{11} & Ω_{12} & Ω_{13} & h A^{T} Z_{2} \\ * & Ω_{22} & Ω_{23} & 0 \\ * & * & Ω_{33} & 0 \\ * & * & * & - Z_{2} \end{matrix}],$

$\begin{array}{l} {\tilde{Θ}}_{11} = A^{T} P_{1} + P_{1} A + Q_{1} + 2 α_{1} P_{1} - e^{- α_{1} h} Z_{1}, {\tilde{Θ}}_{12} = P_{1} B U K - e^{- α_{1} h} (S_{1} - Z_{1}), {\tilde{Θ}}_{13} = e^{- α_{1} h} S_{1}, {\tilde{Θ}}_{14} = P_{1} B U K, \\ {\tilde{Θ}}_{22} = δ Φ - e^{- α_{1} h} (2 Z_{1} - S_{1} - S_{1}^{T}), {\tilde{Θ}}_{23} = - e^{- α_{1} h} (S_{1} - Z_{1}), {\tilde{Θ}}_{24} = δ Φ, {\tilde{Θ}}_{33} = - e^{- α_{1} h} (Q_{1} + Z_{1}), {\tilde{Θ}}_{44} = δ Φ - Φ, \\ Ω_{11} = A^{T} P_{2} + P_{2} A + Q_{2} - α_{2} P_{2} - Z_{2}, Ω_{12} = Z_{2} - S_{2}, Ω_{13} = S_{2}, Ω_{22} = S_{2} + S_{2}^{T} - 2 Z_{2}, Ω_{23} = Z_{2} - S_{2}, \\ Ω_{33} = - e^{α_{2} h} Q_{2} - Z_{2}, \end{array}$

则下列不等式成立

$V (t) \leq {\begin{cases} e^{- α_{1} (t - h_{n - 1})} V_{1} (h_{n - 1}), t \in ν_{k, n} \cap L_{1, n - 1} \\ e^{α_{2} (t - h_{n - 1} - l_{n - 1})} V_{2} (h_{n - 1} + l_{n - 1}), t \in L_{2, n - 1} . \end{cases}$ (18)

证明. 考虑下面两种情况。

(i) $\forall t \in ν_{k, n} \cap L_{1, n - 1}$ ，误差 $e_{k, n} (t)$ 满足

$e_{k, n}^{T} (t) Φ e_{k, n} (t) \leq δ {[x (t - τ_{k, n} (t)) + e_{k, n} (t)]}^{T} Φ [x (t - τ_{k, n} (t)) + e_{k, n} (t)] .$ (19)

对 $V_{1} (t)$ 沿着系统(17)的轨迹关于t求导可得

$\begin{matrix} {\dot{V}}_{1} (t) = - α_{1} V (t) + α_{1} x^{T} (t) P_{1} x (t) + 2 x^{T} (t) P_{1} \dot{x} (t) - x^{T} (t - h) e^{- α_{1} h} P_{1} x (t - h) \\ + h^{2} {\dot{x}}^{T} (t) Z_{1} \dot{x} (t) - h \int_{t - h}^{t} {\dot{x}}^{T} (s) e^{- α_{1} (t - s)} Z_{1} \dot{x} (s) d s \\ \leq - α_{1} V (t) + α_{1} x^{T} (t) P_{1} x (t) + 2 x^{T} (t) P_{1} \dot{x} (t) - x^{T} (t - h) e^{- α_{1} h} P_{1} x (t - h) \\ + h^{2} {\dot{x}}^{T} (t) Z_{1} \dot{x} (t) - h e^{- α_{1} h} \int_{t - h}^{t} {\dot{x}}^{T} (s) Z_{1} \dot{x} (s) d s . \end{matrix}$ (20)

根据引理2可得，如果存在 $[\begin{matrix} Z_{1} & S_{1} \\ * & Z_{1} \end{matrix}] > 0$ ，有

$- h \int_{t - h}^{t} {\dot{x}}^{T} (s) Z_{1} \dot{x} (s) d s \leq - ς^{T} (t) [\begin{matrix} Z_{1} & S_{1} - Z_{1} & - S_{1} \\ * & 2 Z_{1} - S_{1} - S_{1}^{T} & S_{1} - Z_{1} \\ * & * & Z_{1} \end{matrix}] ς (t) .$ (21)

其中 $ς (t) = {[x^{T} (t), x^{T} (t - τ_{k, n} (t)), x^{T} (t - h)]}^{T}$ 。

结合条件(19)~(21)可得

${\dot{V}}_{1} (t) \leq - α_{1} V (t) + ξ^{T} (t) (Θ + h^{2} Γ_{1}^{T} Z_{1} Γ_{1}) ξ (t),$ (22)

其中

$ξ (t) = {[x^{T} (t), x^{T} (t - τ_{k, n} (t)), x^{T} (t - h), e_{k, n}^{T} (t)]}^{T},$

$Θ = [\begin{matrix} Θ_{11} & Θ_{12} & Θ_{13} & Θ_{14} \\ * & Θ_{22} & Θ_{23} & Θ_{24} \\ * & * & Θ_{33} & 0 \\ * & * & * & Θ_{44} \end{matrix}], Γ_{1}^{T} = [\begin{matrix} A^{T} \\ {(B Ξ K)}^{T} \\ 0 \\ {(B Ξ K)}^{T} \end{matrix}],$

$\begin{array}{l} Θ_{11} = A^{T} P_{1} + P_{1} A + Q_{1} + α_{1} P_{1} - e^{- α_{1} h} Z_{1}, Θ_{12} = P_{1} B Ξ K - e^{- α_{1} h} (S_{1} - Z_{1}), Θ_{13} = e^{- α_{1} h} S_{1}, \\ Θ_{14} = P_{1} B Ξ K, Θ_{22} = δ Φ - e^{- α_{1} h} (2 Z_{1} - S_{1} - S_{1}^{T}), Θ_{23} = - e^{- α_{1} h} (S_{1} - Z_{1}), Θ_{24} = δ Φ, \\ Θ_{33} = - e^{- α_{1} h} (Q_{1} + Z_{1}), Θ_{44} = δ Φ - Φ . \end{array}$

根据Schur补引理 [18]，可得(16)式等价于

$\tilde{ϒ} + ρ φ φ^{T} + ρ^{- 1} ψ^{T} ψ < 0.$ (23)

利用引理2，(23)式成立能够确保 $\tilde{ϒ} + φ ψ^{T} + ψ φ^{T} < 0$ 成立。

根据 $| E | \leq L \leq I$ ，进而有 $\tilde{ϒ} + φ E ψ^{T} + ψ E^{T} φ^{T} < 0$ 。

由 $Ξ = U (I + E)$ ，可得

$ϒ = [\begin{matrix} Θ & h Γ_{1}^{T} Z_{1} \\ * & - Z_{1} \end{matrix}] < 0.$ (24)

对(24)式应用Schur补引理，可得 $Θ + h^{2} Γ_{1}^{T} Z_{1} Γ_{1} < 0$ 。

根据(22)式，有下列不等式成立

${\dot{V}}_{1} (t) \leq - α_{1} V (t) .$ (25)

对(25)式积分，可得

$V_{1} (t) < e^{- α_{1} (t - h_{n - 1})} V_{1} (h_{n - 1}) .$

(ii) $\forall t \in L_{2, n - 1}$ ，类似(i)的证明，可得式(17)成立保证下列不等式成立

${\dot{V}}_{2} (t) \leq α_{2} V (t) .$ (26)

对(26)式积分，我们有

$V_{2} (t) < e^{α_{2} (t - h_{n - 1} - l_{n - 1})} V_{2} (h_{n - 1} + l_{n - 1}) .$

综合(i)和(ii)，得(18)式成立。证明完毕。

接下来给出系统(15)的有限时间稳定性的充分条件。

定理2. 给定DoS攻击参数 $υ_{1} \geq 0$ ， $τ_{D} \geq h$ ，反馈增益矩阵K，正常数 $c_{1}, c_{2}, T_{f}$ ， $c_{1} < c_{2}$ ，正定矩阵R。令 $P_{i} = R^{\frac{1}{2}} {\tilde{P}}_{i} R^{\frac{1}{2}}$ ， $Q_{i} = R^{\frac{1}{2}} {\tilde{Q}}_{i} R^{\frac{1}{2}}$ ， $Z_{i} = R^{\frac{1}{2}} {\tilde{Z}}_{i} R^{\frac{1}{2}}$ ， $i \in {1, 2}$ ，如果对于给定常数 $α_{i} > 0$ ， $μ_{i} > 0 (μ_{1} μ_{2} > 1)$ ， $0 < δ < 1$ ， $ρ > 0$ ，存在矩阵 $P_{i} > 0$ ， $Φ > 0$ ， $Q_{i} > 0$ ， $Z_{i} > 0$ ，S，使得式(16)~(17)，以及下列条件成立

$P_{1} \leq μ_{2} P_{2},$ (27)

$P_{2} \leq μ_{1} e^{(α_{1} + α_{2}) h} P_{1},$ (28)

$Q_{i} \leq μ_{3 - i} Q_{3 - i},$ (29)

$Z_{i} \leq μ_{3 - i} Z_{3 - i},$ (30)

$(λ_{2} + λ_{3} h) c_{1} < \frac{c_{2}}{M},$ (31)

其中 $λ_{1} = \min {λ_{\min} ({\tilde{P}}_{i})}$ ， $λ_{2} = λ_{\max} ({\tilde{P}}_{1}) + h λ_{\max} ({\tilde{Q}}_{1})$ ， $λ_{3} = \frac{h^{2}}{2} λ_{\max} ({\tilde{Z}}_{1})$ ，则系统(15)是关于 $(c_{1}, c_{2}, T_{f}, R)$ 有限时间稳定的。

证明. 利用(27)~(30)，我们有

$V_{1} (h_{n - 1}) \leq μ_{2} V_{2} (h_{n - 1}^{-}),$ (32)

$V_{2} (h_{n - 1} + l_{n - 1}) \leq μ_{1} e^{(α_{1} + α_{2}) h} V_{1} [{(h_{n - 1} + l_{n - 1})}^{-}] .$ (33)

对 $t \in [0, T_{f})$ ，存在 $n \in ℕ$ 使得 $t \in L_{1, n - 1}$ 或 $t \in L_{2, n - 1}$ 。

根据式(18)，(32)和(33)，当 $t \in L_{1, n - 1}$ ，我们有

$\begin{matrix} V_{1} (t) \leq e^{- α_{1} (t - h_{n - 1})} V_{1} (h_{n - 1}) \\ \leq μ_{2} e^{- α_{1} (t - h_{n - 1})} V_{2} (h_{n - 1}^{-}) \\ \leq μ_{2} e^{- α_{1} (t - h_{n - 1})} e^{α_{2} (h_{n - 1} - h_{n - 2} - l_{n - 2})} V_{2} (h_{n - 2} + l_{n - 2}) \\ \leq μ_{1} μ_{2} e^{- α_{1} (t - h_{n - 1})} e^{α_{2} (h_{n - 1} - h_{n - 2} - l_{n - 2})} e^{(α_{1} + α_{2}) h} V_{2} [{(h_{n - 2} + l_{n - 2})}^{-}] \\ ⋮ \\ \leq e^{n (t) (α_{1} + α_{2}) h + n (t) \ln (μ_{1} μ_{2})} V_{1} (0) e^{d}, \end{matrix}$ (34)

其中 $d = α_{2} (h_{n - 1} - h_{n - 2} - l_{n - 2} + h_{n - 2} - h_{n - 3} - l_{n - 2} + \dots + h_{1} - h_{0} - l_{0}) - α_{1} (l_{n - 2} + \dots + l_{1} + l_{0})$ 。

结合定义1和假设，可得

$V_{1} (t) \leq e^{g_{1}} V_{1} (0),$ (35)

其中 $g_{1} = (υ_{1} + \frac{T_{f}}{τ_{D}}) \times (α_{1} + α_{2}) h + α_{2} b_{\max} (υ_{1} + \frac{T_{f}}{τ_{D}}) - α_{1} l_{\min} (υ_{1} + \frac{T_{f}}{τ_{D}}) + (υ_{1} + \frac{T_{f}}{τ_{D}}) \ln (μ_{1} μ_{2})$ 。

另一方面，当 $t \in L_{2, n - 1}$ ，我们有

$V_{2} (t) \leq \frac{1}{μ_{2}} e^{g_{2}} V_{1} (0),$ (36)

其中 $g_{2} = (υ_{1} + \frac{T_{f}}{τ_{D}} + 1) \times (α_{1} + α_{2}) h + α_{2} b_{\max} (υ_{1} + \frac{T_{f}}{τ_{D}} + 1) - α_{1} l_{\min} (υ_{1} + \frac{T_{f}}{τ_{D}} + 1) + (υ_{1} + \frac{T_{f}}{τ_{D}} + 1) \ln (μ_{1} μ_{2})$ 。

根据 $V (t)$ 的定义，可得

$V (t) \geq λ_{1} x^{T} (t) R x (t), V_{1} (0) \leq (λ_{2} + λ_{3} h) c_{1},$ (37)

其中 $c_{1} = \sup_{θ \in [- h, 0]} {x^{T} (θ) R x (θ), {\dot{x}}^{T} (θ) R \dot{x} (θ)}$ 。

令 $M = \max {\frac{e^{g_{1}}}{λ_{1}}, \frac{e^{g_{2}}}{λ_{1} μ_{2}}}$ ，结合(31)和(37)，可得

$x^{T} (t) R x (t) \leq M V_{1} (0) \leq M (λ_{2} + λ_{3} h) c_{1} < c_{2} .$

根据定义2，系统(15)是关于 $(c_{1}, c_{2}, T_{f}, R)$ 有限时间稳定的。证明完毕。

3.2. 鲁棒可靠性控制器设计

下面的定理给出了系统(15)基于事件触发的可靠性状态反馈控制器的设计。

定理3. 给定DoS攻击参数 $υ_{1} \geq 0$ ， $τ_{D} \geq h$ ，正常数 $c_{1}, c_{2}, T_{f}$ ， $c_{1} < c_{2}$ ，正定矩阵R。令 $P_{i} = R^{\frac{1}{2}} {\tilde{P}}_{i} R^{\frac{1}{2}}$ ， $Q_{i} = R^{\frac{1}{2}} {\tilde{Q}}_{i} R^{\frac{1}{2}}$ ， $Z_{i} = R^{\frac{1}{2}} {\tilde{Z}}_{i} R^{\frac{1}{2}}$ ， $i \in {1, 2}$ ，如果对于给定常数 $α_{i} > 0$ ， $μ_{i} > 0 (μ_{1} μ_{2} > 1)$ ， $0 < δ < 1$ ， $ρ > 0$ ，存在矩阵 $X_{i} > 0$ ， $\hat{Φ} > 0$ ， ${\hat{Q}}_{i} > 0$ ， ${\hat{Z}}_{i} > 0$ ， $\hat{S}$ ，Y，使得条件(31)以及下列不等式成立

${\hat{Σ}}_{1} > 0, {\hat{Π}}_{1} < 0,$ (38)

${\hat{Σ}}_{2} > 0, {\hat{Π}}_{2} < 0,$ (39)

$[\begin{matrix} - μ_{2} X_{2} & X_{2}^{T} \\ * & - X_{1} \end{matrix}] \leq 0,$ (40)

$[\begin{matrix} - μ_{1} e^{(α_{1} + α_{2}) h} X_{1} & X_{1}^{T} \\ * & - X_{2} \end{matrix}] \leq 0,$ (41)

$[\begin{matrix} - μ_{3 - i} {\hat{Q}}_{3 - i} & X_{3 - i}^{T} \\ * & {\hat{Q}}_{i} - 2 X_{i} \end{matrix}] \leq 0,$ (42)

$[\begin{matrix} - μ_{3 - i} {\hat{Z}}_{3 - i} & X_{3 - i}^{T} \\ * & {\hat{Z}}_{i} - 2 X_{i} \end{matrix}] \leq 0,$ (43)

其中

${\hat{Σ}}_{1} = [\begin{matrix} {\hat{Z}}_{1} & {\hat{S}}_{1} \\ * & {\hat{Z}}_{1} \end{matrix}], {\hat{Σ}}_{2} = [\begin{matrix} {\hat{Z}}_{2} & {\hat{S}}_{2} \\ * & {\hat{Z}}_{2} \end{matrix}], {\hat{Π}}_{1} = [\begin{matrix} \hat{ϒ} & \hat{φ} & \hat{ψ} \\ * & - ρ^{- 1} I & 0 \\ * & * & - ρ I \end{matrix}], \hat{ϒ} = [\begin{matrix} \hat{Θ} & h {\hat{Γ}}_{1}^{T} Z_{1} \\ * & - Z_{1} \end{matrix}],$

${\hat{Γ}}_{1}^{T} = [\begin{matrix} X A^{T} \\ {(B U Y)}^{T} \\ 0 \\ {(B U Y)}^{T} \end{matrix}], \hat{φ} = [\begin{matrix} B \\ 0 \\ 0 \\ \begin{array}{l} 0 \\ h B \end{array} \end{matrix}], \hat{ψ} = [\begin{matrix} \begin{array}{l} 0 \\ Y^{T} U^{T} \end{array} \\ 0 \\ Y^{T} U^{T} \\ 0 \end{matrix}], \hat{Θ} = [\begin{matrix} {\hat{Θ}}_{11} & {\hat{Θ}}_{12} & {\hat{Θ}}_{13} & {\hat{Θ}}_{14} \\ * & {\hat{Θ}}_{22} & {\hat{Θ}}_{23} & {\hat{Θ}}_{24} \\ * & * & {\hat{Θ}}_{33} & 0 \\ * & * & * & {\hat{Θ}}_{44} \end{matrix}], {\hat{Π}}_{2} = [\begin{matrix} {\hat{Ω}}_{11} & {\hat{Ω}}_{12} & {\hat{Ω}}_{13} & h X_{2} A^{T} \\ * & {\hat{Ω}}_{22} & {\hat{Ω}}_{23} & 0 \\ * & * & {\hat{Ω}}_{33} & 0 \\ * & * & * & {\hat{Z}}_{2} - 2 X_{2} \end{matrix}],$

$\begin{array}{l} {\hat{Θ}}_{11} = X_{1} A^{T} + A X_{1} + {\hat{Q}}_{1} + α_{1} X_{1} - e^{- α_{1} h} {\hat{Z}}_{1}, {\hat{Θ}}_{12} = B U Y - e^{- α_{1} h} ({\hat{S}}_{1} - {\hat{Z}}_{1}), {\hat{Θ}}_{13} = e^{- α_{1} h} {\hat{S}}_{1}, {\hat{Θ}}_{14} = B U Y, \\ {\hat{Θ}}_{22} = δ \hat{Φ} - e^{- α_{1} h} (2 {\hat{Z}}_{1} - {\hat{S}}_{1} - {\hat{S}}_{1}^{T}), {\hat{Θ}}_{23} = - e^{- α_{1} h} ({\hat{S}}_{1} - {\hat{Z}}_{1}), {\hat{Θ}}_{24} = δ \hat{Φ}, {\hat{Θ}}_{33} = - e^{- α_{1} h} ({\hat{Q}}_{1} + {\hat{Z}}_{1}), \\ {\hat{Θ}}_{44} = δ \hat{Φ} - \hat{Φ}, {\hat{Ω}}_{11} = X_{2} A^{T} + A X_{2} + {\hat{Q}}_{2} - α_{2} X_{2} - {\hat{Z}}_{2}, {\hat{Ω}}_{12} = {\hat{Z}}_{2} - {\hat{S}}_{2}, {\hat{Ω}}_{13} = {\hat{S}}_{2}, {\hat{Ω}}_{22} = {\hat{S}}_{2} + {\hat{S}}_{2}^{T} - 2 {\hat{Z}}_{2}, \\ {\hat{Ω}}_{23} = {\hat{Z}}_{2} - {\hat{S}}_{2}, {\hat{Ω}}_{33} = - e^{α_{2} h} {\hat{Q}}_{2} - {\hat{Z}}_{2}, \end{array}$

则系统(15)关于 $(c_{1}, c_{2}, T_{f}, R)$ 有限时间稳定，状态反馈增益为 $K = Y X_{1}^{- 1}$ 。

证明. 定义 $X_{i} = P_{i}^{- 1}$ ， ${\hat{Q}}_{i} = X_{i} Q_{i} X_{i}$ ， ${\hat{Z}}_{i} = X_{i} Z_{i} X_{i}$ ， $i = 1, 2$ ， $\hat{Φ} = X_{1} Φ X_{1}$ ， $Y = K X_{1}$ ，则控制器增益为 $K = Y X_{1}^{- 1}$ 。根据引理3，有 $- X_{1} {\hat{Z}}_{1}^{- 1} X_{1} \leq {\hat{Z}}_{1} - 2 X_{1}$ 成立。分别对条件(16)中两式两边同时乘以 $d i a g {X_{1}, X_{1}}$ ， $d i a g {X_{1}, X_{1}, X_{1}, X_{1}, Z_{1}^{- 1}, I, I}$ ，可得条件(38)中成立。分别对式(27)和(28)两边同乘 $X_{2}$ 和 $X_{1}$ ，可得(40)和(41)分别等价于(27)和(28)。利用类似的方法，可得式(17)成立能够保证式(39)成立，(42)~(43)成立能够保证(29)~(30)成立。根据定理2，条件(31)，(38)~(43)成立能够保证系统(15)关于 $(c_{1}, c_{2}, T_{f}, R)$ 有限时间稳定。证明完毕。

当系统含有不确定性时，控制器设计如下。

定理4. 给定DoS攻击参数 $υ_{1} \geq 0$ ， $τ_{D} \geq h$ ，正常数 $c_{1}, c_{2}, T_{f}$ ， $c_{1} < c_{2}$ ，正定矩阵R。令 $P_{i} = R^{\frac{1}{2}} {\tilde{P}}_{i} R^{\frac{1}{2}}$ ， $Q_{i} = R^{\frac{1}{2}} {\tilde{Q}}_{i} R^{\frac{1}{2}}$ ， $Z_{i} = R^{\frac{1}{2}} {\tilde{Z}}_{i} R^{\frac{1}{2}}$ ， $i \in {1, 2}$ ，如果对于给定常数 $α_{i} > 0$ ， $μ_{i} > 0 (μ_{1} μ_{2} > 1)$ ， $0 < δ < 1$ ， $ρ > 0$ ，存在矩阵 $X_{i} > 0$ ， $\hat{Φ} > 0$ ， ${\hat{Q}}_{i} > 0$ ， ${\hat{Z}}_{i} > 0$ ， $\hat{S}$ ，Y，使得条件(31)，(40)~(43)以及下列不等式成立

${\hat{Σ}}_{1} > 0, {\hat{Ψ}}_{1} < 0,$ (44)

${\hat{Σ}}_{2} > 0, {\hat{Ψ}}_{2} < 0,$ (45)

其中

${\hat{Ψ}}_{1} = [\begin{matrix} {\hat{Π}}_{1} & N_{1} & M_{1} \\ * & - ν_{1}^{- 1} I & 0 \\ * & * & - ν_{1} I \end{matrix}], {\hat{Ψ}}_{2} = [\begin{matrix} {\hat{Π}}_{2} & N_{2} & M_{2} \\ * & - ν_{2}^{- 1} I & 0 \\ * & * & - ν_{2} I \end{matrix}],$

$\begin{array}{l} N_{1}^{T} = [F_{1} X_{1}, F_{2} U Y, 0, F_{2} U Y, 0, F_{2}, 0], N_{2}^{T} = [F_{1} X_{2}, 0, 0, 0], \\ M_{1}^{T} = [E^{T}, 0, 0, 0, h E^{T}, 0, 0], M_{2}^{T} = [E^{T}, 0, 0, h E^{T}], \end{array}$

则系统(14)关于 $(c_{1}, c_{2}, T_{f}, R)$ 鲁棒有限时间稳定，且状态反馈增益为 $K = Y X_{1}^{- 1}$ 。

证明. 在式(38)~(39)中，分别用 $A + Δ A (t)$ 和 $B + Δ B (t)$ 替代A和B，结合条件(2)，可得

${\hat{Π}}_{1} + N_{1} H^{T} (t) M_{1}^{T} + M_{1} H (t) N_{1}^{T} < 0,$ (46)

${\hat{Π}}_{2} + N_{2} H^{T} (t) M_{2}^{T} + M_{2} H (t) N_{2}^{T} < 0.$ (47)

根据引理2，存在正常数 $ν_{1}, ν_{2}$ ，(46)和(47)分别等价于下列不等式

${\hat{Π}}_{1} + ν_{1} N_{1} N_{1}^{T} + ν_{1}^{- 1} M_{1} M_{1}^{T} < 0,$ (48)

${\hat{Π}}_{2} + ν_{2} N_{2} N_{2}^{T} + ν_{2}^{- 1} M_{2} M_{2}^{T} < 0.$ (49)

利用Schur补引理，可得(48)等价于 ${\hat{Ψ}}_{1} < 0$ ，(49)等价于 ${\hat{Ψ}}_{2} < 0$ 。根据定理3，条件(31)，(40)~(45)能保证系统(14)是鲁棒有限时间稳定的。证明完毕。

4. 数值仿真

在本节中，我们给出两个仿真例子来验证所提出的控制器设计方法对DoS攻击下网络控制系统的有效性。

例1. 考虑系统(15)具有如下参数

$A = [\begin{matrix} 0.1 & - 0.9 \\ 1.1 & - 0.4 \end{matrix}], B = [\begin{matrix} - 0.1 & 0.3 \\ - 0.4 & 0.2 \end{matrix}],$

执行器故障矩阵为

$Ξ = d i a g {d_{1}, d_{2}},$

其中 $0.2 \leq d_{1} \leq 0.8$ ， $0.3 \leq d_{2} \leq 0.7$ 。

令 $c_{1} = 1$ ， $c_{2} = 20$ ， $T_{f} = 10$ ， $R = I$ ， $δ = 0.15$ ， $α_{1} = 0.05$ ， $α_{2} = 0.3$ ， $h = 0.02$ ， $μ_{1} = μ_{2} = 1.01$ ， $ρ = 1$ ， $l_{\min} = 1.5$ ， $b_{\max} = 0.2$ 。根据定理3，可得事件触发矩阵和可靠性控制器增益如下

$Φ = [\begin{matrix} 2.4099 & - 0.8564 \\ - 0.8564 & 1.3069 \end{matrix}], K = [\begin{matrix} - 5.0894 & 5.7539 \\ - 5.2299 & 1.7458 \end{matrix}] .$

例2. 考虑系统(1)具有如下参数

$A = [\begin{matrix} - 0.5 & - 1 \\ 0.7 & 0.45 \end{matrix}], B = [\begin{matrix} 0.5 & - 0.2 \\ - 0.3 & - 0.7 \end{matrix}],$ (50)

$E = [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}], F_{1} = [\begin{matrix} 0.02 & 0 \\ 0 & 0.2 \end{matrix}], F_{2} = [\begin{matrix} 0.1 & 0 \\ 0 & 0.01 \end{matrix}] .$ (51)

执行器故障矩阵同例1。令 $c_{1} = 1$ ， $c_{2} = 20$ ， $T_{f} = 10$ ， $R = I$ ， $δ = 0.1$ ， $α_{1} = 0.05$ ， $α_{2} = 0.3$ ， $h = 0.02$ ， $μ_{1} = μ_{2} = 1.01$ ， $ρ = 0.7$ ， $ϑ_{1} = ϑ_{2} = 0.9$ ， $l_{\min} = 1.5$ ， $b_{\max} = 0.2$ 。通过解定理4中的线性矩阵不等式，可得如下矩阵参数

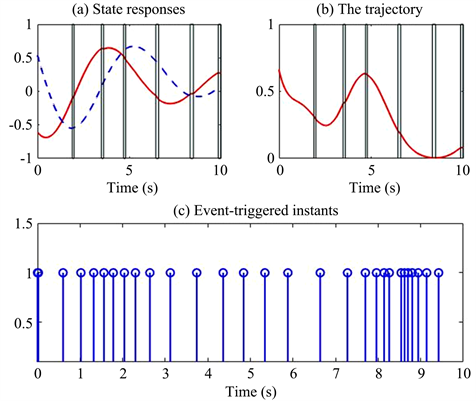
$Φ = [\begin{matrix} 0.3995 & 0.4398 \\ 0.4398 & 0.9713 \end{matrix}], K = [\begin{matrix} - 1.2305 & - 0.2816 \\ 0.8515 & 1.4221 \end{matrix}] .$

Figure 2. The state responses, the trajectory of $x^{T} (t) R x (t)$ and the event trigger time of the system (1) with the parameters (50), (51)

图2. 具有参数(50)，(51)的系统(1)的状态响应， $x^{T} (t) R x (t)$ 的轨迹，事件触发时刻

令系统状态以及误差的初始值为 ${[- 0.61, 0.54]}^{T}$ ， ${[0, 0]}^{T}$ ，通过Matlab仿真可得图2，其中图2(a)为系统的状态响应，红色实线表示 $x_{1} (t)$ ，蓝色虚线表示 $x_{2} (t)$ ，阴影部分表示DoS攻击区间；图2(b)为 $x^{T} (t) R x (t)$ 的轨迹图2(c)为事件触发时刻。从仿真结果，我们可以得到，网络控制系统(1)是关于 $(1, 20, 10, I)$ 鲁棒有限时间稳定的。

5. 结论

本文研究了在执行器故障和非周期DoS攻击下网络控制系统基于事件触发机制的鲁棒有限时间镇定问题。考虑到非周期DoS攻击的影响，设计了合适的事件触发机制避免在DoS攻击区间采样，且保证在DoS攻击结束时能及时更新信息。根据建模的类似切换的时滞系统模型，构造了分段Lyapunov-Krasovskii泛函，得到了保证系统有限时间稳定的条件，还给出了事件触发矩阵和鲁棒可靠控制器的联合设计。

基金项目

在此对“国家自然科学基金”，基金号61573007的资助表示感谢。

文章引用

薛梦洁,王为群,李天瑞. DoS攻击下不确定网络控制系统基于事件触发机制的鲁棒有限时间可靠控制
Robust Finite-Time Reliable Control for Uncertain Networked Control Systems under Denial of Service Attacks Based on Event Triggering Mechanism[J]. 动力系统与控制, 2022, 11(03): 104-116. https://doi.org/10.12677/DSC.2022.113012

参考文献

1. Zhang, X.M., Han, Q.L., Ge, X.H., et al. (2020) Networked Control Systems: A Survey of Trends and Techniques. IEEE/CAA Journal of Automatica Sinica, 7, 17.
https://doi.org/10.1109/JAS.2019.1911651

2. Wang, X.F. and Lemmon, M.D. (2011) Event-Triggering in Distributed Networked Control Systems. IEEE Transactions on Automatic Control, 56, 586-601.
https://doi.org/10.1109/TAC.2010.2057951

3. Yue, D., Tian, E.G. and Han, Q.L. (2013) A Delay System Method for Designing Event-Triggered Controllers of Networked Control Systems. IEEE Transactions on Automatic Control, 58, 475-481.
https://doi.org/10.1109/TAC.2012.2206694

4. Amin, S., Crdenas, A.A. and Sastry, S.S. (2009) Safe and Secure Networked Control Systems under Denial-of-Service Attacks. International Conference on Hybrid Systems: Computation and Control, San Francisco, 13-15 April 2009, 31-45.
https://doi.org/10.1007/978-3-642-00602-9_3

5. Du, D.J., Zhang, C.D., Wang, H.K., et al. (2018) Stability Analysis of Token-Based Wireless Networked Control Systems under Deception Attacks. Information Sciences, 459, 168-182.
https://doi.org/10.1016/j.ins.2018.04.085

6. Zhu, M.H. and Martinez, S. (2013) On the Performance Analysis of Resilient Networked Control Systems under Replay Attacks. IEEE Transactions on Automatic Control, 59, 804-808.
https://doi.org/10.1109/TAC.2013.2279896

7. Chen, X.L., Wang, Y.G. and Hu, S.L. (2018) Event-Based Robust Stabilization of Uncertain Networked Control Systems under Quantization and Denial-of-Service Attacks. Information Sciences, 459, 369-386.
https://doi.org/10.1016/j.ins.2018.05.019

8. Chen, X.L., Wang, Y.G. and Hu, S.L. (2019) Event-Triggered Quantized H∞ Control for Networked Control Systems in the Presence of Denial-of-Service Jamming Attacks. Nonlinear Analysis: Hybrid Systems, 33, 265-281.
https://doi.org/10.1016/j.nahs.2019.03.005

9. Elahi, A. and Alfi, A. (2018) Finite-Time Stability Analysis of Uncertain Network-Based Control Systems under Random Packet Dropout and Varying Network Delay. Nonlinear Dynamics, 91, 713-731.
https://doi.org/10.1007/s11071-017-3905-3

10. Dorato, P. (1961) Short-Time Stability in Linear Time-Varying Systems. Proceedings of the IRE International Convention Record Part 4, New York, 9 May 1961, 83-87.

11. Mathyalagan, K., Park, J. and Sakthivel, R. (2016) Finite-Time Boundedness and Dissipativity Analysis of Networked Cascade Control Systems. Nonlinear Dynamics, 84, 2149-2160.
https://doi.org/10.1007/s11071-016-2635-2

12. Wu, J.C., Peng, C., Zhang J., et al. (2020) Event-Triggered Finite-Time H∞ Filtering for Networked Systems under Deception Attacks. Journal of the Franklin Institute, 357, 3792-3808.
https://doi.org/10.1016/j.jfranklin.2019.09.002

13. Foroush, H.S. and Martinez, S. (2016) On Triggering Control of Single-Input Linear Systems under Pulse-Width Modulated DoS Signals. SIAM Journal on Control and Optimization, 54, 3084-3105.
https://doi.org/10.1137/16M1069390

14. Persis, C.D. and Tesi, P. (2015) Input-to-State Stabilizing Control under Denial-of-Service. IEEE Transactions on Automatic Control, 60, 2930-2944.
https://doi.org/10.1109/TAC.2015.2416924

15. Zha, L.J., Liu, J.L. and Cao, J.D. (2020) Security Control for T-S Fuzzy Systems with Multi-Sensor Saturations and Distributed Event-Triggered Mechanism. Journal of Franklin Institute, 357, 2851-2867.
https://doi.org/10.1016/j.jfranklin.2020.02.013

16. Xie, L.H. (1996) Output Feedback H∞ Control of Systems with Parameter Uncertainty. International Journal of Control, 63, 741-750.
https://doi.org/10.1080/00207179608921866

17. Xiong, J.L. and Lam, J. (2009) Stabilization of Networked Control Systems with a Logic ZOH. IEEE Transactions on Automatic Control, 54, 358-363.
https://doi.org/10.1109/TAC.2008.2008319

18. 俞立. 鲁棒控制——线性矩阵不等式处理方法[M]. 北京: 清华大学出版社, 2002: 6-11.

期刊菜单